Прогнозирование сроков сохраняемости изделий в условиях воздействия прямого солнечного излучения

В настоящее время на открытом воздухе в наземных условиях эксплуатируется большинство изделий. Эксплуатация изделий на открытом воздухе ставит их в условия неблагоприятного воздействия климатических факторов (температуры и влажности воздуха, солнечной радиации и т. п.). В результате этого воздействия ухудшаются свойства конструкционных материалов изделий и снижаются сроки их служебной пригодности.

Особый интерес представляет изучение влияния повышенных температур и солнечного излучения на тепловое состояние изделий, содержащих узлы и элементы из полимерных материалов, эксплуатируемых в странах с тропическим климатом. Тепловое состояние изделий может оказывать значительное влияние на срок сохраняемости изделий. В предлагаемой работе задача решается численным моделированием с использованием метода конечных элементов.

Математическая постановка задачи в дифференциальной форме описывается уравнением не стационарной теплопроводности в полярной системе координат:

д Т  Лд²Т 1 д Т  1 д ² Т

ср— = Л „,+ дт ^ дr2   r дr  r2 дф2

где с - удельная теплоемкость; р - плотность; т - время; Л - коэффициент теплопроводности;

r - радиус; ф - угол.

Уравнение (1) дополняется начальным условием

T (r,Ф,0) = То и граничным условием 2-го рода q^ = f (R ф, т) на поверхности S2,                                                       (3)

или граничным условием 3-го рода

– λ = α ( Т – Т ) на поверхности S                                                (4)

∂r на наружной поверхности изделия, Т0, R – начальная температура и наружный радиус изделия; α – коэффициент теплоотдачи; Тс – температура окружающей среды.

Приближенное решение уравнения (1) с начальным (2) и граничными (3) и (4) условиями приводится к вариационной постановке задачи о нахождении минимума функционала J [1]:

δJ (T(r, φ, τ)) = 0, где δ – символ вариации, J – функционал, то есть функция, зависящая от значений другой функции.

Для плоской задачи нестационарной теплопроводности, то есть для поперечного сечения изделия, функционал J представляется в виде:

J = J {0,5[ X ( d T / д r )² + X ( d T / дф )²] - ( Q -p c( d T / дт ) Т } dV + J q ₂ dS + J ( a T ²/2 -a TT c ) dS .

v                                                                           S 2 S 3

Реализация вариационной постановки задачи методом конечных элементов приводит к получению разрешающего дифференциально-матричного уравнения в форме

[C] ^{∂ {T}} + [ Κ ] ⋅ { Τ } = {F},                                                                             (5)

∂τ где [C], [K] и {F} – глобальные матрицы теплоемкости, теплопроводности, вектор тепловых на- грузок и {Τ} – вектор узловых температур.

Для получения решения уравнения (5) пошаговым методом его необходимо привести к матрично-алгебраическому виду. С этой целью воспользуемся его конечно-разностной аппроксимацией по времени. Запишем уравнение (5) в виде

[C] κ ⋅ ^{∂ { Τ } κ} + [K] κ ⋅ { Τ } κ = {F} κ ,                                                                     (6)

κ_∂ τ   κκκ

κ здесь параметры с индексом « к » соответствуют времени тк = т0 + ^ Атi, i=1

где τ 0 – начало отсчета времени, в частности τ 0 = 0 .

∂ { Τ }    { Τ } - { Τ }

С использованием левосторонней разности κ ≈ κκ1 уравнение (6) прини-∂τ Δτ мает вид

-L[C] k + [К] к | { Т } к = -^[С] к { Т } к- 1 + {F} к .

(^Ат к            J       ^Ат к

Полученное выражение (7) представляет собой разрешающее матрично-алгебраическое уравнение для определения неизвестных температур в узловых точках дискретной схемы изделия в конце каждого временного шага Δτ и непосредственно используется для составления вычислительной программы.

Рассмотрено решение задачи при граничных условиях 2-го рода с учетом суточного и годового движения Солнца. Полагаем, что на каждый элемент поверхности изделия падает тепловой поток q 2 = qp+ q к+ q л+ q з, где qp ,qκ ,qл и qз – радиационная, конвективная, лучистая и отраженная от поверхности земли составляющие теплового потока.

Для расчета q p использовано соотношение q _p = I _s ⋅β _c ⋅ D _а ⋅cosθ ,

где I_s – солнечная постоянная, равная 4,873∙10⁶ кДж/(м²∙ ч) [2]; D _а – коэффициент прозрачности атмосферы, принимаем D _а = 0,82 [3]; θ – угол между направлением солнечных лучей и нормалью к поверхности элемента; β _с – коэффициент поглощения поверхностью изделия.

Для определения cos θ используется формула из работы [2]

cos θ = sin δ sin ϕ cos S – sin δ cos ϕ sin S cos γ + cos δ cos ϕ cos S cos w +

+ cos δ sin ϕ sin S cos γ cos w + cos δ sin S sin γ sin w .                                         (9)

Обозначение углов δ , ϕ , S , γ , w приведены в работе [2].

Выражения (8) и (9) позволяют рассчитывать приход солнечной энергии на каждый элемент поверхности изделия в любое время конкретных суток года для конкретной местности.

Конвективная составляющая qκ определяется по закону Ньютона qκ = α(Tc-T0), где α – коэффициент теплоотдачи.

Для определения коэффициента α использованы критериальные зависимости для поперечного обтекания воздушным потоком одиночной горизонтальной трубы из работы [4].

Лучистая составляющая теплового потока определяется теплообменом между наружной поверхностью изделия и небосводом [2]:

qл=βс⋅σ⋅(Tэ4ф-T04), где βс – коэффициент поглощения поверхностью изделия; σ – постоянная Стефана-Больцмана, σ = 5,668∙10–8 Вт/(м2∙К4); Tэф – эффективная температура небосвода, определяемая выражением

T _эф = 0,0552∙ T _c ^1,5.

Составляющая, определяющая поток от земной поверхности к элементу поверхности расчетного сечения изделия, имеет вид [2]

qз =βcρзqpz(1-cosS)/2 , где ρз – диффузная отражательная способность земной поверхности по отношению к солнечному излучению, в расчетах принято ρз = 0,2 [2]; qpz – составляющая потока солнечной радиации, падающая на горизонтальную поверхность qpz=Is ⋅Dacosθz, где cosθz =sinδsinϕ+cosδcosϕcosw.

Состав изделия, принятого к расчету, геометрические размеры и теплофизические характеристики составляющих элементов приведены в табл. 1.

Таблица 1

Состав, геометрические размеры и теплофизические характеристики

Номер элемента	Конструкционный элемент	Радиус, мм	λ , Вт/(м∙К)	С, Дж/(кг∙К)	ρ , кг/м3
1	Полимерный блок	20/60	0,2326	1255	1500
2	Теплозащитное покрытие	60/65	0,2907	1255	1200
3	Воздушный зазор	65/70	0,0267	1004	1,25
4	Теплозащитное покрытие	70/75	0,2326	1255	1200
5	Стальной корпус	75/78	34,89	502	7800
6	Воздушный зазор	78/83	0,0267	1004	1,25
7	Корпус контейнера	83/88	0,0174	1255	1800

Для численного решения задачи поперечное сечение изделия представлялось в виде конечноэлементной сетки в полярной системе координат r – φ с числом узлов NУ = 555, числом конечных элементов NE = 1008, с шириной полуполосы ленточной термической матрицы системы

SH = 17. При этом в направлении радиуса r выбрано 15 точек деления (узлов) с неравномерным шагом Δ r , а в направлении угла φ 37 – точек деления (узлов) с равномерным шагом Δφ = 10° от 0 до 360° (то есть NУ = 15×37 = 555). Для автоматической дискретизации поперечного сечения изделия использовались плоские треугольные конечные элементы.

Расчеты проведены для региона с сухим тропическим климатом [5, с. 7–9]. Выбор обусловлен несколькими причинами: во-первых, в этом регионе высока энергетическая экспозиция солнечного излучения, во-вторых, для этого региона имеются необходимые для проведения расчета статистические данные многолетних наблюдений температуры окружающей среды.

Поскольку в стандарте [5] статистическая информация о температуре окружающей среды представлена в виде среднемесячных температур и среднесуточных перепадов, потребовался прием перехода от среднемесячных значений температур среды ( T _с.м ) к текущим ( T_i ). В расчетах для этих целей использовано выражение

T i = T с.м – Δ T /2sin( π /2 +τ y ), (10) где Δ T – среднемесячный суточный перепад (ход) температуры; τ _y – угловое время суточного движения (хода) температуры.

Алгоритм расчета углового времени τ _y таков, чтобы для каждых суток обеспечивалось выполнение двух условий: на восходе солнца температура окружающего воздуха минимальна, а в 14 ч 30 мин местного солнечного времени она достигает суточного максимума.

В табл. 2 с использованием исходных данных по ГОСТ 24482-80 представлен рассчитанный по изложенному алгоритму суточный ход температуры для региона с сухим тропическим климатом на 1 августа. При этом время восхода солнца выбирается согласно работе [2].

Таблица 2

Зависимость температуры воздуха T i от времени суток τ y

τ y , ч	1	2	3	4	5	6	7	8	9	10	11	12
T i , °С	30,1	28,9	27,9	27,0	26,4	26,1	26,0	26,9	28,9	31,6	34,6	37,4
τ y , ч	13	14	15	16	17	18	19	20	21	22	23	24
T i , °С	39,6	40,8	41,0	40,7	40,2	39,4	38,4	37,3	35,9	34,5	33,1	31,5

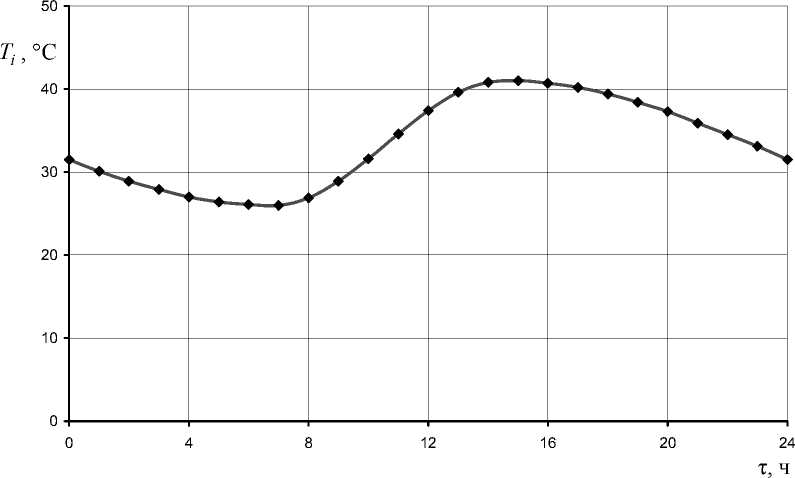
Рис. 1. Зависимость температуры воздуха от времени суток

По изложенному алгоритму рассчитывается распределение температур в изделии за характерный промежуток времени эксплуатации (обычно за один год).

Для прогноза и обоснования сроков сохраняемости изделий из полимерных материалов в настоящее время широко используется параметр «эквивалентная температура» ( Т экв ). Переход от годового распределения температуры (по времени) в какой-то конкретной, выбранной исходя из целей решаемой задачи, зоне изделия к эквивалентной температуре осуществляется согласно ГОСТ [6].

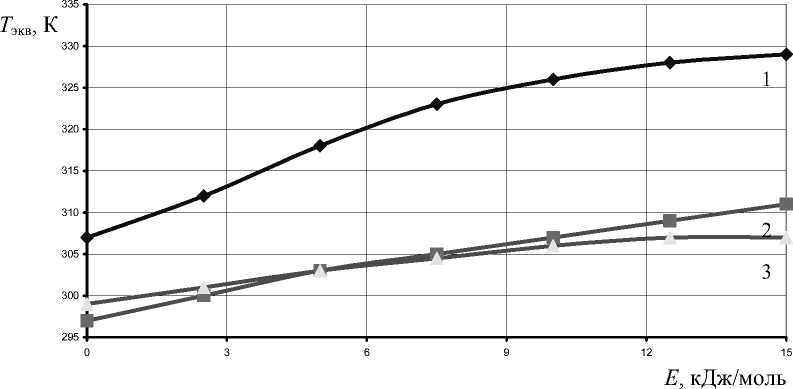
Рис. 2. Расчетные значения Т экв . Изделие вне контейнера: 1 – поверхность изделия темного цвета (β с = 0,8); 2 – поверхность изделия светлого цвета (β с = 0,26);

3 – изделие под навесом

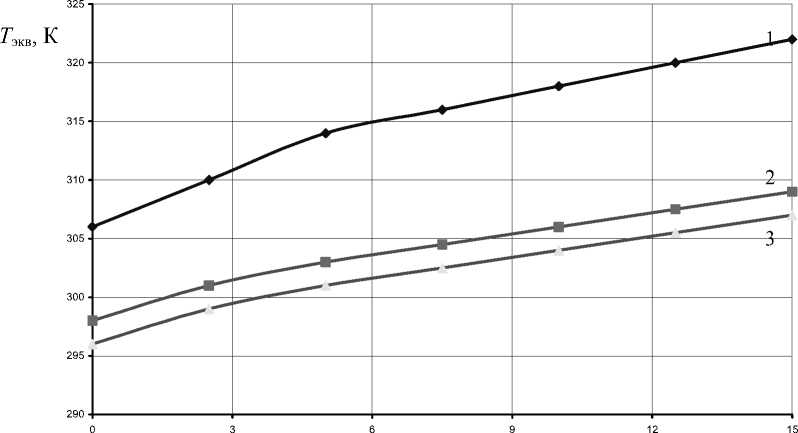
Е , кДж/моль

Рис. 3. Расчетные значения Т экв . Изделие в контейнере: 1 – поверхность изделия темного цвета (β с = 0,8); 2 – изделие под навесом;

3 – поверхность изделия светлого цвета (β с = 0,26)

Результаты расчетов представляются в виде зависимостей эквивалентных температур эксплуатации от температурного коэффициента (Е) процесса старения полимерного материала, определяющего срок сохраняемости изделия. На рис. 2–4 приведены результаты расчетов.

На рис. 2 и 3 представлены результаты расчета для центральной зоны (R = 4 см) полимерного блока, на рис. 4 – для зоны контакта «полимерный блок – теплозащитное покрытие» (R = 6 см).

Во всех случаях расчеты выполнены для точек, лежащих на радиусе, направленном под углом 45° к горизонту в западном направлении – в этой зоне суточные температуры в элементах изделия максимальны.

Для случая высокой теплозащищенности расчетной зоны наличие нескольких теплозащитных слоев и светоотражающей внешней поверхности, рассчитанные с учетом воздействия прямой солнечной радиации значения эквивалентных температур (рис. 2, кривая 2 и рис. 3, кривая 3) близки к таковым, определенным по данным метеонаблюдений. По данным стандарта [5] для условий под навесом: рис. 2, кривая 3, или рис. 3, кривая 2. С увеличением коэффициента поглощения внешней поверхностью вклад солнечной радиации становится весьма значимым (рис. 2, кривая 1 и рис. 3, кривая 1), в этом случае возрастает теплозащитная роль внешнего контейнера.

На рис. 4 представлены результаты расчетов для зоны изделия, расположенной ближе к поверхности и соответственно менее теплозащищенной, чем середина полимерного блока. В этом случае вклад солнечной радиации значим даже для изделий с поверхностью, обладающей низким коэффициентом поглощения.

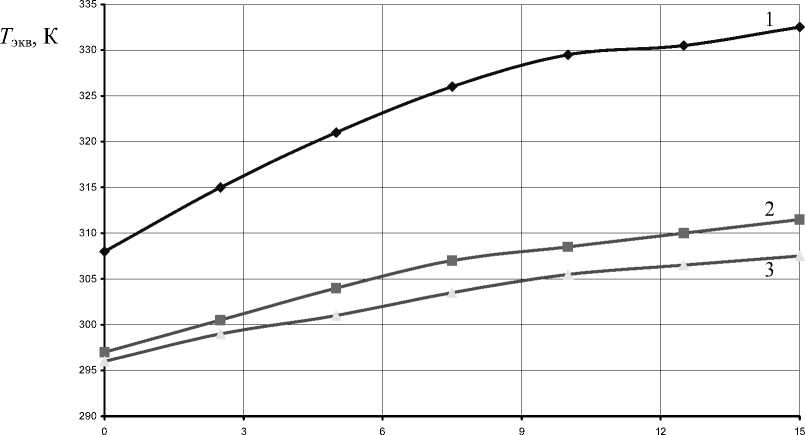
Е , кДж/моль

Рис. 4. Расчетные значения Т экв . Изделие вне контейнера:

1 – поверхность изделия темного цвета (β с = 0,8); 2 – поверхность изделия светлого цвета (β с = 0,26); 3 – изделие под навесом

Для экспериментального подтверждения срока сохраняемости изделий, принимая конкретную температуру форсированного старения ( Т фс ), с помощью уравнения Аррениуса

E lg τ фс = lg τ экс - 4 75

^ экв фс у рассчитывается время старения τфс , проводится форсированное старение изделия и последующее его испытание.

Заключение. Разработан и реализован в виде вычислительной программы конечноэлементный метод расчета текущих значений температур и эквивалентных температур эксплуатации изделий с учетом воздействия прямой солнечной радиации с учетом суточного и годового движения Солнца.