Прогнозирование структур белков методами полуопределенного программирования

Особое внимание в литературе уделяется решению задачи предсказания упаковки боковых цепей. В статьях [3, 4] описаны одни из лучших по качеству и скорости методов решения задачи упаковки боковых цепей. В ранних работах М.Е. Карасикова и Ю.В. Максимова также рассмотрена задача предсказания упаковки боковых цепей белковой структуры при помощи выпуклой оптимизации в предположении известного положения основной цепи. Важно отметить, что задача прогнозирования структур является N P -трудной задачей квадратичной оптимизации. Проблема упаковки белковых молекул в комплекс связана с исследованием большого числа всевозможных вариантов структур белка (большой размер базового пространства поиска).

Перейдем к формальной постановке задачи: предположим, что в цепи имеется п белков, причем каждый г-й белок может располагаться в одной из р позиций: ж ^г = [ж 1 ,ж 2 , ...,ж р ], где ж ^ € { 0,1 } . Для типичных макроструктур предполагается п ~ 10, р ~ 100. Тогда одному комплексу будет соответствовать вектор ж = [ж ¹ ,..., ж ^п ] ^т . Любой паре позиций ж р и ж т можно приписать функцию энергии q, которая обусловлена силовым взаимодействием. Каждой позиции белка также соответствует собственное значение энергии Ь о (эти значения получены из экспериментальных данных). Обозначим через N число всевозможных позиций белков, составляющих один комплекс.

Тогда задача оптимальной упаковки может быть записана в виде задачи минимизации:

жтQoж + Ьтж ^ min

0      же{о,1Р при условии, что Аж = 1n, где бинарная матрица А размера N хп имеет единичное значение г—1

элемента А-ij, если и только если j : ^2 Pt < j 6 ^L Pt. А матрица Qo имеет вид t=i

Q o =	[0] [q 2i (P 2 ,P i )] . .	[q i2 (P i ,P 2 )]    • [0]             • .. .	•    [q in (P 1 ,P n )] •    [q 2n (P 2 ,P n )] . .. .
	. . [q n i ( P n ,P i )]	. [q »2 (P n ,P 2 )]    •	.. • •              [0]

В общем случае, матрица Q o не является положительно полуопределенной. Одна из формулировок задачи записывается как невыпуклая оптимизация. Изначально задача задана на булевом кубе: Bn = { ж : ж г € { 0,1 } , 1 6 г 6 п } . Замечая, что ж^тQ o ж = (Q o ,жж^т ) n,n , переходим к задаче выпуклой оптимизации. С использованием различных методов релаксации можно попытаться получить приближенное решение исходной задачи с высокой точностью за полиномиальное время.

Решение задачи определяется размерностями и свойствами матрицы Q o : в случае малых размерностей достаточно воспользоваться жадными алгоритмами, а в случае больших размерностей предлагается воспользоваться методами выпуклой оптимизации: например, полуопределенной релаксацией, релаксацией Лагранжа. Целью данной статьи является построение алгоритма меньшей вычислительной сложности с использованием предложенных методов [5–8].

т = ігр ~ 1000 и являются сильно разреженными (доля нулевых элементов составляет порядка 99%).

Целью работы является исследование задачи квадратичной оптимизации, возникающей при решении проблемы оптимальной упаковки белков, и повышение эффективности методов выпуклой оптимизации за счет ее структуры.

• 3.    Используемые алгоритмы

• 3.1.    Полуопределенная релаксация

Для снижения вычислительной сложности исходной невыпуклой задачи квадратичной булевой оптимизации, являющейся N P -трудной, осуществляется переход к графовой структуре данных (построение описано ниже), а затем задача декомпозируется древесным образом. В процессе используются различные эвристические методы – например, работа с хордальным расширением полученного графа. В результате это приводит к решению задачи за меньшее время в сравнении с обычной полуопределенной релаксацией. Перейдем непосредственно к описанию используемых методов.

При использовании методов выпуклой оптимизации для решения задачи 1 невыпуклые ограничения заменяются на более слабые, но выпуклые ограничения. Тогда мы переходим к выпуклой задаче, методы решения которой хорошо известны. В результате удается получить хорошую оценку в задачах поиска минимума значения целевой функции. Основным методом выпуклой релаксации, рассматриваемым в этой работе, является полуопределен-ная релаксация.

Полуопределенную релаксацию можно представить в виде

52 Q ⁱi ^Х ^

min ,

X GS + ,$ > 0 v

где 5 ^ = { Xn,n : X = X ^т ^ 0 } и, кроме того, X ^ хх ^т , Хц = Хі, г = 1,..., N и Ах = 1 „ . Используя лемму Шура, перепишем задачу в виде эквивалентной:

E Q ij X ij ^    min

X gRV xV ,$>0v при дополнительных условиях [X х; хт 1] € 5^ +1, Хц = Хі, г = 1,..., N, Ах = 1„. Метод реализуется на MatLab при использовании пакета сих.

• 3.2.    Хордальная структура данных

Для снижения вычислительной сложности алгоритма воспользуемся результатами из теории графов. Заметим, что каждой квадратной матрице Q o порядка п в соответствие можно поставить некоторый граф G с п вершинами, ребра которого строятся по следующим правилам: наличию ненулевого элемента { г, j } в матрице Q o соответствует ребро, соединяющее вершины г и J. Если же элемент {г, J } в матрице Q o равен 0, ребро между элементами г и j не проводится.

Определение 1. Граф называется хордальным , если каждый из его циклов, имеющий четыре и более дуг, имеет хорду, которая является ребром, соединяющим две вершины, не смежные в цикле.

Поставим задачу поиска максимальных клик в графе G. Поскольку про структуру таблицы смежности исходного графа ничего не известно, то можно считать, что граф G является произвольным. В общем случае задача поиска максимальных клик является NP -полной. Однако для исходных графов можно построить хордовое расширение и, воспользовавшись свойствами этих графов, получить решение этой задачи за полиномиальное время. В нашей работе для построения расширения использовался элиминационный алгоритм [12], состоящий из трех основных шагов:

• 1)    в графе G = ( V, Е ) на п вершинах фиксируем некоторый порядок просмотра вершин ст. Пусть G ₁ = G, Е ’ = 0 ;

• 2)    добавим ребра к G t так, чтобы все соседи вершины г стали попарно смежными. Добавленные ребра включим во множество Е ‘ и удалим из графа G t вершину г получив граф G t+i ;

• 3)    вычислим хордовое расширение G' = (V;Е U Е ‘ ) графа G.

Для полученного хордового расширения воспользуемся теоремой [9].

Теорема 1. Пусть матрице X соответствует граф G, К 1 ,...,К д - максимальные клики графа G. Тогда следующие условия эквивалентны:

• 1)    Можно дополнить X до положительно полуопределенной матрицы;

• 2)    Х к _і ,к _і ^ 0, г = 1,...,d, — подматрица X с номерами строк и стобцов, принадлежащими K t .

Тогда при решении задачи 1 для тех матриц энергий, для которых размер максимальной клики у соответствующего ей графа существенно меньше размера этого графа, заменим исходную полуопределенную релаксацию на ее модификацию: поиск минимума не по всем X, удовлетворяющим необходимым условиям, а по отдельным подматрицам существенно меньших размеров, соответствующих вершинам, входящим в состав максимальных клик.

Приведем теоретические факты и алгоритмы, используемые для вычисления максимальных клик в хордальных графах за полиномиальное время [11, 12].

Следующий алгоритм (MSC, maximum cardinality search) вычисляет совершенный порядок исключения вершин графа G = (V, Е ) на п вершинах:

• 1)    для всех вершин v Е V положим l[v] = 0;

• 2)    для всех г, 1 6 г 6 п, выберем непронумерованную вершину v с наибольшим значением l[v] и положим ct ( v ) = г. Для всех смежных с v вершин ш в графе G увеличим 1[ш] на единицу.

Порядок ст на графе G, полученный в результате работы указанного алгоритма, есть совершенный порядок исключения вершин графа G, если граф хордальный.

Теорема 2. Неориентированный граф является хордальным тогда и только тогда, когда алгоритм MSC вычисляет (G, ст), где ст является совершенным порядком исключения для графа G.

Теорема 3. Каждая максимальная клика хордального графа G = (V, Е ) имеет вид { v } U X(v), где X (v) = { w Е adj ( v ) | ct ( v ) <  ct ( w ) } , adj (v) - множество вершин, смежных с v в графе G.

Теорема 4. Хордальный граф имеет не более, чем п максимальных клик.

Алгоритм вычисления максимальных клик для хордального графа G = (V, Е ) на п вершинах и совершенного порядка исключения ст имеет вид:

• 1)    для всех вершин v Е V инициализируем параметр размера s[v] = 0;

• 2)    для всех г, 1 6 г 6 п, положим v = ст ^-1 (г) и

• •    если степень вершины d(v) = 0, то возвращаем максимальную клику {v}, •    вычисляем множество X = {w : (v, w) Е Е и ct(v) < ct(w)}, •    если множество X непусто и s[v] < |X|, то возвращаем максимальную клику {v} U X. Иначе обновим оценку расстояния s[m[v]] = max{s[m[v]], |X| — 1} для вершины m[v] = CT-1(min{CT(w)|w Е X});

• 3)    в качестве ответа алгоритм возвращает набор всех максимальных клик.

• 4.    Вычислительный эксперимент

  Матрицы энергий (379 штук) из PDB (Protein Database Bank) были разбиты на группы по количеству вершин в соответствующих графах: до 500 (малых размеров), 500–1000 (средних размеров), больше 1000 (больших размеров). Для графов из каждой категории (73 – в первой категории, 145 – во второй и 161 – в третьей соответственно) были построены хордальные расширения и вычислены размеры максимальных клик. Приведем результаты в табл. 1.

В результате от NР -полной задачи нахождения максимальных клик переходим к задаче для хордальных графов, решаемой за полиномиальное время.

Таблица1

Соотношение размеров графов и их максимальных клик в исследуемой выборке

размер клики	<12	12–16	16–20	>20
менее 500 вершин	4	29	32	8
500–1000 вершин	1	41	87	16
более 1000 вершин	0	16	120	25

Для исходной матрицы энергий из выборки приведем графики зависимости, на которых по оси абсцисс откладываются фиксированные размеры, а по оси ординат отложим число графов, размер максимальных клик которых не превосходит это фиксированное число.

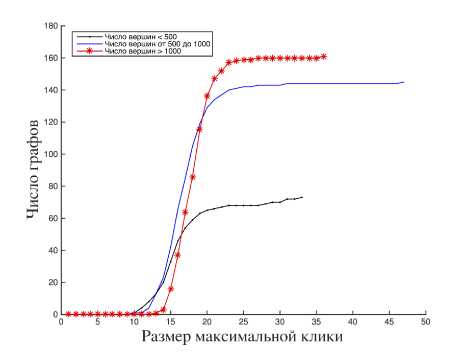
Рис. 1. Размеры максимальных клик

Учитывая приведенные выше обоснования, делаем вывод, что на исходной выборке следует попробовать применить модификацию исходной полуопределенной релаксации. На исходной выборке из PDB можно сравнить скорость и точность работы полуопределенной релаксации с/без использования хордовой структуры данных, и сопоставить их методу Монте-Карло.

Вычислив максимальные клики для графов, соответствующих матрицам энергий, можно перейти к работе с методами релаксации. Была изучена зависимость времени работы SDP, SDP с учетом хордальной структуры данных и Монте-Карло от размеров исходных матриц.

Сравнивались средние времена работы исходного SDP и модифицированной задачи на всей выборке из 379 матриц. Было получено, что в среднем на любой матрице из выборки модифицированная задача решается в 3.24 раза быстрее.

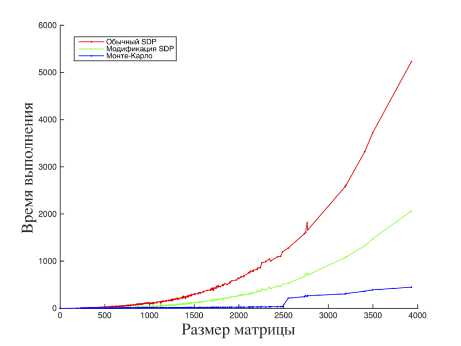
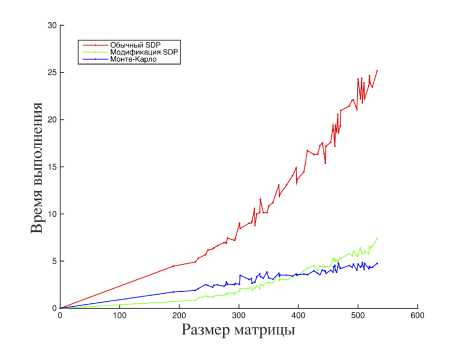
Рис. 3. Вычислительная сложность для матриц малых размерностей

Рис. 2. Вычислительная сложность для матриц всех размерностей

Также можно посмотреть, в скольких случаях модифицированный SDP дает значения целевой функции быстрее метода Монте-Карло. На нашей выборке первый метод давал результаты быстрее на 11% исходной выборки. В среднем метод работал быстрее на квадратных матрицах размера 200–300. Если задать допустимую точность вычисления значения целевой функции 5 = 5%, то расчет показывает, что в сравнении со стохастическим методом Монте-Карло модифицированный SDP дает более точное значение целевой функции на 2.84% матриц, на которых он работает быстрее.

Таблица2

Задачи с наибольшим выигрышем в скорости модифицированного SDP алгоритма

id	SDP		Модифицированный SDP		Монте-Карло		Размер
	Значение	Время	Значение	Время	Значение	Время
1ado	13452	4.91	13624	0.85	12439	1.9	227
1b9w	15995	11.51	16201	2.48	15416	3.36	336
1cei	15830	10.16	15088	2.06	14717	3.66	335
1f94	13937	5.69	14006	1.31	13131	2.51	244
1gvp	16686	9.22	15184	1.91	15696	2.65	322
1oai	12595	6.62	11859	1.28	11599	2.56	258
1uln	14269	7.44	14079	1.61	13699	2.56	281
1ulr	16295	7.42	14294	1.66	15004	2.64	294
1wm3	14278	7.22	13305	1.57	12751	2.5	292
2g30	11522	6.96	11578	1.36	11508	2.33	275
2gqv	11427	4.39	11609	0.68	10371	1.76	190
1yu5	12412	6.19	11704	1.31	12255	2.32	258
1yzm	8757.2	4.54	8197.3	0.73	7995.7	1.7	190

Приведена таблица с указанием времени работы трех методов на части выборки, для которой соответствующие квадратные матрицы энергий имеют размеры до 500 строк (столбцов), и полученным значением минимизируемого функционала. Под id понимается метка данной белковой структуры, а под размером – размер соответствующей матрицы энергий Q o . В табл. 2 приводятся результаты, в которых хордальная модификация показала наиболее высокие результаты по сравнению с другими методами.

Вместе с тем следует отметить, что в ряде случаев качество методов полуопределен-ной релаксации существенно выше, чем качество методов Монте-Карло. Пять задач с наи- большим выигрышем в качестве решения методами полуопределенного программирования приведены в табл. 3.

Таблица3

Задачи с наибольшим выигрышем в качестве полуопределенной релаксации

id	SDP		Модифицированный SDP		Монте-Карло		Размер
	Значение	Время	Значение	Время	Значение	Время
2hpl	18169	13.52	17641	3.62	19199	3.95	398
2o0q	20229	14.06	17866	3.35	18621	3.41	390
2i49	16099	10.83	14929	2.73	15683	3.23	350
2fl4	18492	11.91	17055	2.97	18310	3.41	368
1ulr	16295	7.42	14294	1.66	15004	2.64	294

• 5.    Заключение

В данной работе рассмотрены алгоритмы прогнозирования четвертичных структур белков, построенных на основе предположения о минимизации суммарной энергии. Для невыпуклой задачи оптимизации были рассмотрены методы выпуклой релаксации как без учета хордальной структуры данных, так и с учетом этой структуры. Был проведен вычислительный эксперимент на основе данных из PDB. Проведено сравнение результатов работы этих двух алгоритмов и метода Монте-Карло. Показано, что в задачах малой размерности использованние выпуклой релаксации с хордальной структурой позволяет повысить скорость решения. В целом точность решения методами полуопределенной релаксации и методом Монте-Карло примерно равна, что по всей видимости связано с особенностями порождения данных задачи.

Использованная в работе идея из [10] заключалась в разбиении исходной задачи полу-определенной релаксации на подзадачи определенным способом и последующим решением подзадач также методами полуопределенной релаксации. Дальшейшее повышение точности результатов возможно за счет явного представления оптимума в небольших кликах в виде последовательности максимумов, решаемой явно и встраивании данной конструкции в двойственную задачу.

В работе было показано, что в ряде задач структурной биологии данные обладают необходимыми свойствами для проведения эффективной декомпозиции исходной задачи на задачи меньшей вычислительной сложности (например, использованная в статье хордальная структура данных). В ряде случаев удается получить существенный выигрыш в скорости и качестве решения поставленной задачи.