Прогнозирование уровня жизни населения Республики Коми методом корреляционного и регрессионного анализа

Автор: Андреева О.Ю.

Журнал: Экономика и социум @ekonomika-socium

Статья в выпуске: 5-1 (18), 2015 года.

Бесплатный доступ

В статье описан процесс прогнозирования уровня жизни населения Республики Коми методом корреляционного и регрессионного анализа с помощью программы «Excel». Рассмотрены модели парной и множественной линейной регрессии. Описан расчет точечного и интервального прогнозов эндогенного показателя. Определены результаты прогнозирования в сравнении с фактическими данными.

Прогнозирование, регрессионный анализ, корреляционный анализ, точечный прогноз, интервальный прогноз

Короткий адрес: https://sciup.org/140114516

IDR: 140114516

Текст научной статьи Прогнозирование уровня жизни населения Республики Коми методом корреляционного и регрессионного анализа

Уровень жизни населения является одной из важнейших социальных категорий. Изучение динамики данного показателя, его прогнозирование, очень важно для устойчивого и сбалансированного развития общества, т.к. это способствует:

1) Выявлению тенденций в развитии общества;
2) Установлению связей между отдельными социальноэкономическими и политическими процессами;
3) Подготовке информационной базы для управленческих решений;
4) Предсказанию последствий принятых решений.

Для прогнозирования показателей уровня жизни населения

Республики Коми использовалcя метод корреляционного и регрессионного анализа.

На первом этапе прогнозирования был определен состав экзогенных показателей за 2004-2013 гг., под влиянием которых формируются значения эндогенного показателя «Среднедушевые денежные доходы населения в месяц», руб. (Y) (таб.1). Объем выборки составил 6 показателей:

• Среднемесячная номинальная начисленная заработная плата работников организаций, руб. (X1);
• Средний размер назначенных месячных пенсий, руб. (X2);
• Величина прожиточного минимума (в на душу населения), руб. в месяц (X3);
• Численность пенсионеров, тыс. чел. (X4);
• Приватизировано жилых помещений всего, тыс. ед. (X5);
• Жилищный фонд в среднем на одного жителя, м2 (X6).

Таблица 1 – Эндогенный и экзогенные показателя для прогнозирования

Год	Y	X1	X2	X3	X4	X5	X6
2004	9301	9482	2547	3135	273,6	207,9	22,3
2005	11247	11612	3183	3624	278,1	222,3	22,6
2006	13418	14082	3579	4290	279,1	235,5	22,9
2007	16216	17077	4694	4980	282,6	242,6	23,2
2008	18636	20638	5856	6108	282,9	248	23,4
2009	20085	23686	7942	6810	284,9	258,4	24,3
2010	22260	26140	9613	7349	290,7	264,4	24,7
2011	23925	28897	10502	8192	293,2	266,9	25
2012	27040	33971	11643	8246	294,5	271,7	25,4
2013	29335	37717	12800	9161	295,5	280,3	25,5

По правилу 3х сигм было выяснено, что аномальных значений нет, т.к. показатели не выходят за верхнюю и нижнюю границы интервала по правилу 3х сигм (таб. 2).

Таблица 2 – Расчеты для проверки аномальных значений

№	Y	X1	X2	X3	X4	X5	X6
Х средний	19146,3	22330,2	7235,9	6189,5	285,51	249,8	23,93
Дисперсия	4450241 4	90020664	1,4E+07	442088	57,799	528,98	1,4223
Сигма	6671,01	9487,92	3761,6	2102,6	7,6026	22,99	1,1926
3 Сигмы	20013,0	28463,8	11285	6307,8	22,808	68,99	3,5779
Мах и min значение разброса (интервал)	39159,3	50793,9	18521	12497	308,32	318,8	27,508
Мах и min значение разброса (интервал)	-866,73	-6133,57	-4049	-118,26	262,70	180,80	20,35

Далее была построена корреляционная матрица (таб. 3), которая показывает, между какими переменными есть значимая корреляция, и какой характер она носит (сильная, средняя, слабая). Все выбранные показатели значимо коррелируют друг с другом, при это связь корреляции сильная (> 0,9).

Таблица 3– Корреляционная матрица

	Y	X1	X2	X3	X4	X5	X6
Y	1
X1	0,99683	1
X2	0,98488	0,989733	1
X3	0,9908	0,985679	0,98599	1
X4	0,98029	0,974793	0,9812	0,97667	1
X5	0,97949	0,96525	0,95531	0,98047	0,96824	1
X6	0,9821	0,983474	0,99534	0,98488	0,98375	0,96655	1

Связь
Сильная	\|Rxy\|≥0,7
Средняя	0,3≤\|Rxy\|<0,7
Слабая	\|Rxy\|<0,3

При построении моделей парной регрессии по каждому показателю выяснилось, что все экзогенные показатели модели значимо влияют на эндогенный, так как показатели F-статистики больше критической точки (таб. 4).

Таблица 4 – Проверка значимости влияния экзогенных показателей на эндогенный

Объясня ющие переменн ые	Кол-во объясня ющих переменн ых	Коэф. детерми нации	Скорректир ованный коэф. детерминац ии	F- статист ика	Критиче ская точка F (кр)	Значимо сть
X1	1	0,9936	0,9928	1256,97	5,3176	значимо
X2	1	0,9699	0,9662	258,620	5,3176	значимо
X3	1	0,9816	0,9793	428,781	5,3176	значимо
X4	1	0,9609	0,9560	196,966	5,3176	значимо
X5	1	0,9594	0,9543	189,07	5,3176	значимо
X6	1	0,9645	0,9600	217,445	5,3176	значимо

Далее была построена модель множественной линейной регрессии, в которую были включены все экзогенные показатели. В целом полученная модель статистически значима (таб. 5).

Таблица 5 – Проверка значимости модели множественной линейной регрессии

Объясняющие переменные	Кол-во объясняющих переменных	Коэф. детерми нации	F -статистика	Крит. точка Fкр	Значимост ь модели
X1, X2, X3, X4, X5, X6	p = 6	0,999	539,323	8,941	значима

Далее методом пошагового исключения были исключены незначимые показатели. Первым был исключен показатель X6 – «Жилищный фонд в среднем на одного жителя», т.к. по модулю его t-статистика была наименьшей (-0,1707), затем - показатель X5 «Приватизировано жилых помещений всего» (t-статистика = 0,9390), после чего все оставшиеся показатели стали значимыми.

Таким образом, была получена модель с четырьмя экзогенными показателями:

Y= - 47318,74 + 0,62 * Среднемесячная номинальная начисленная зарплата работников организаций - 0,74 * Средний размер назначенных месячных пенсий + 1,04 * Величина прожиточного минимума + 180,26 * Численность пенсионеров

Разница между новым уравнением и исходным статистически не значима (F-статистика = 0,1742, F критическая = 6,3882).

Далее был рассчитан точечный прогноз среднедушевых денежных доходов населения в месяц (эндогенного показателя) на 2014 г. Фактические значения экзогенных показателей были взяты из статистического сборника «Республика Коми в цифрах» (таб. 6).

Таблица 6 – Фактические значения эндогенных показателей

Показатель	Значение
X1 - Среднемесячная номинальная начисленная з/п	39739
X2 - Средний размер назначенных месячных пенсий, руб.	13925
X3 - Величина прожиточного минимума (в среднем на душу населения)	10439
X4 - Численность пенсионеров, тыс. чел.	296
Среднедушевые денежные доходы населения в месяц, руб.	30724

Точечный прогноз: Y = - 47318,74 + 0,62*X1 - 0,74*X2 + 1,04*X3 +

180,26*X4 = 31228,46

Таким образом, среднедушевые денежные доходы населения в месяц по прогнозу на 2014 г. составили 31228,46 руб., в то время как фактическое значение этого показателя – 30724 руб. Погрешность составила 1 %.

Для построения доверительного прогноза необходимо знание ковариационной матрицы оценок коэффициентов уравнения:

В = д2(ХТХ)-1,

где X - матрица наблюдений, Х^т - транспонированная матрица , д² -оценка остаточной дисперсии.

Cначала строится матрица наблюдений (таб. 7).

Таблица 7 – Матрица наблюдений

X=	X1	X2	X3	X4
1	9482	2547	3135	273,6
1	11612	3183	3624	278,1
1	14082	3579	4290	279,1
1	17077	4694	4980	282,6
1	20638	5856	6108	282,9
1	23686	7942	6810	284,9
1	26140	9613	7349	290,7
1	28897	10502	8192	293,2
1	33971	11643	8246	294,5
1	37717	12800	9161	295,5

На следующем шаге была построена матрица Х^тХ - произведение матриц X T и X . Это произведение можно найти с помощью функций массива МУМНОЖ(ТРАНСП(массив);массив).

Таблица 8 - Матрица Х^ТХ

10	223302	72359	61895	2855,1
223302	5796564300	1933702973	1559099149	64387782
72359	1933702973	650930897	518050834	20911762
61895	1559099149	518050834	422886967	17812151

Далее находится матрица (Х^ТХ') ¹ , т.е. матрица, обратная к матрице Х^ТХ. Её можно вычислить с помощью функции МОБР(массив).

Таблица 9 - Матрица (ХТХ) 1

4060,58594	0,00023832	0,020636078	0,015723403	-15,10437
0,00023832	7,27656E-08	-1,16377E-07	-1,14501E-07	-1,09E-06
0,02063608	-1,16377E-07	5,66714E-07	-2,25474E-07	-7,27E-05
0,0157234	-1,14501E-07	-2,25474E-07	1,16394E-06	-6,56E-05

Наконец, была рассчитана ковариационная матрица путем умножения ячеек матрицы (Х^ТХ)^-1 на величину д². Среднеквадратическое отклонение остатков д (= 302,37) было выведено из отчета по регрессии с помощью надстройки «Анализ данных», а затем возведено в квадрат: д² = 91429,46.

Таблица 10 - Ковариационная матрица В= 8²(Х^ТХ') ¹

371257199	21,78945558	1886,745559	1437,582336	-1380984
21,7894556	0,00665292	-0,010640327	-0,010468805	-0,100037
1886,74556	-0,010640327	0,051814324	-0,020614952	-6,642401
1437,58234	-0,010468805	-0,020614952	0,106418094	-6,000907
-1380984,3	-0,100036724	-6,642401148	-6,000906713	5143,163

Для нахождения дисперсии прогноза использовалась следующая формула:

s2(fo)= £2+XoBXj,

где B - ковариационная матрица оценок коэффициента уравнения, Х₀ -вектор-строка вида (1,х₁₁₀,.,х_Р10), составленная из заданных значений объясняющих переменных х₁₎₀, .,%_р , ₀ и, соответственно, Х 0 - вектор-столбец. Для вычисления произведения Х₀ВХ 0 использовалась функция МУМНОЖ().

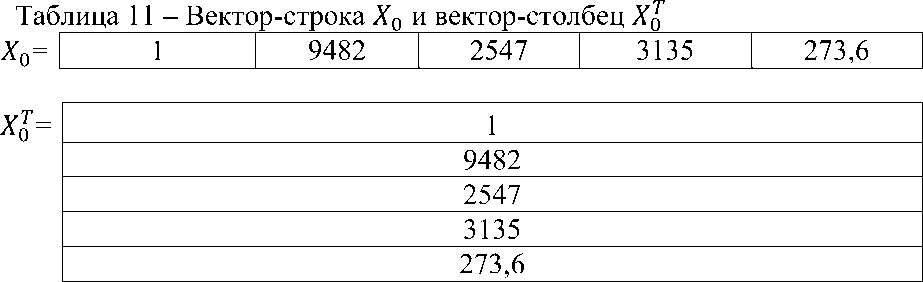
Таблица 12 – Произведение ковариационной матрицы B и вектора- столбца А0_______________________________________________________

вх 0; =	2938854,58	2938854,58	2938854,5	2938854,58	2938854,58
	-2,41821881	-2,41821881	-2,4182188	-2,418218808	-2,418218808
	35,8362332	35,8362332	35,836233	35,83623329	35,83623329
	-22,4165134	-22,4165134	-22,416513	-22,4165134	-22,4165134
	-10494,458	-10494,458	-10494,458	-10494,45804	-10494,45804

Таким образом, Х₀ВХ 0 = 65640,43; а дисперсия прогноза s²(y₀) = ц² + Х₀ВХ 0 = 91429,46 + 65640,43 = 157069,89.

Доверительный прогноз для индивидуальных значений эндогенного показателя при уровне надежности y имеет вид у₀ = у₀ ±5_у, где статистическая погрешность 8_у = t_1-y(n — 3 —р — 1) * s(y₀) = 4,30 *

396,32 = 1705,23.

Таким образом, верхняя граница интервала = 31228,46 + 1705,23 = 32933,69; нижняя граница интервала = 31228,46 - 1705,23 = 29523,23.

Фактические данные за 2014 год попадают в интервальное значение, что говорит о хорошем качестве получившейся модели и о её достоверности, что является важным фактором при прогнозировании.

Список литературы Прогнозирование уровня жизни населения Республики Коми методом корреляционного и регрессионного анализа

Республика Коми в цифрах: краткий статистический сборник/Росстат, Территориальный орган Федеральной службы гос. статистики по Республике Коми. -Сыктывкар, 2015.

Статья научная