Прогнозирование влияния химических активаторов на прочность известково-перлитового вяжущего (ИПВ) методом многоуровневого моделирования

Автор: Танганов Б.Б., Урханова Л.А., Хардаев П.К.

Журнал: Вестник Восточно-Сибирского государственного университета технологий и управления @vestnik-esstu

Статья в выпуске: 1 (36), 2012 года.

Бесплатный доступ

Методом многоуровневого моделирования оценены энергии гидратации ионов химических активаторов. Осуществлено математическое прогнозирование прочности ИПВ в зависимости от видов и количества добавок -различных химических активаторов.

Многоуровневое моделирование, предел прочности, известково-перлитное вяжущее

Короткий адрес: https://sciup.org/142142447

IDR: 142142447

Текст научной статьи Прогнозирование влияния химических активаторов на прочность известково-перлитового вяжущего (ИПВ) методом многоуровневого моделирования

В работе [1] отмечалось, что единой теории, объясняющей механизм действия микродобавок на твердение силикатных систем, не разработано, и в каждом конкретном случае их действие находит свое истолкование. Однако проведенные исследования показывают, что введение химических добавок даже в небольшом количестве ускоряет твердение бесклинкерных композиций и повышает их прочность в среднем в 2-2,5 раза. Установлено, что рост прочности сопровождается увеличением количества химически связанной воды. Результаты исследования физико-химических свойств вяжущих композиций и расчетов характеристик гидратированных ионов свидетельствуют о том, что количество связанной воды зависит от заряда иона и обратно пропорционально радиусу иона, так как воздействие силового поля ядра на молекулы воды при меньшем радиусе иона распространяется на большее число диполей воды.

Гидратное число n s определяется соотношением [2]:

n s = z i e R s ²/ r i p - 3 к Б Т s R² / 2 pe (1)

где R s , z i , r i , р, e , Т и к Б - соответственно радиус молекулы воды, заряд и радиус иона, дипольный момент молекулы воды, диэлектрическая проницаемость воды, температура ( К) и константа Больцмана.

Радиус гидратированного иона rsвычисляется по уравнению rs = (25 zpensh2/3 m!LT-; (2)

В таблице 1 представлены некоторые характеристики гидратированных ионов (гидратные числа, массы и радиусы гидратированных ионов), оцененные по уравнениям (1) и (2).

В процессе разработки концепции многочастичных взаимодействий в растворах сильных и слабых электролитов был предложен метод многоуровневого моделирования (ММУМ), позволяющий математически прогнозировать и моделировать те или иные химические и технологические процессы, а также уточнять или оценивать отсутствующие характеристики химических, физических, биологических, медицинских и других систем [2, 3].

Отметим, что в природе (равно как и во всех естественных науках), хотим мы этого или нет, всё взаимосвязано со всем. Например, если мы пытаемся научиться выращивать большие и вкусные помидоры с заданными свойствами, следует не только на эмпирическом или интуитивном уровне, но, главным образом, на теоретически обоснованном уровне рассматривать факторы , связанные с генетической структурой растений, типом почвы, освещенностью, температурой и т.д. Таким образом, при проведении даже типичного эксперимента приходится иметь дело с большим количеством факторов.

Так, методом многоуровневого моделирования был прогнозирован рост камней в печени партии крыс до летального исхода при холелитиазе, а также выдана прогностическая картина накопления алка- лоидов в лекарственных растениях в различных регионах СФО и ДВФО (например, в районах Бурятии и Забайкальском крае) [4, 5].

ММУМ определяется следующей исходной зависимостью, решаемой в последующем системой из n уравнений [6]:

Y = a + b 1 X 1 + b 2 X 2 + ...+ b_nX_n . (3)

После несложных преобразований найдем, что формула ММУМ с n переменными имеет вид:

Y-y ср = b 1 (X 1 -X 1(ср) +b 2 (X 2 -X 2(ср) +...+b n (X n -X n(ср) ), (4)

причем коэффициенты b 1 , b 2 , ...,b n ММУМ находятся из следующей системы линейных уравнений:

b 1 Σ x 1 ² + b 2 Σ x 1 x 2 + ...+ b n Σ x 1 x n = Σ x 1 y 1 ;

b 1 Σ x 1 x 2 + b 2 Σ x 2 ² + ...+ b n Σ x 2 x n = Σ x 2 y 2 ;

..................

b1Σx1xn + b2Σx2xn + ... + bnΣxn2 = Σxnyn , где приняты нижеследующие обозначения:

Σ x 1 ² = Σ (X 1 -X 1(ср) ); Σ x 1 x 2 = Σ (X 1 -X 1(ср) )(X 2 -X 2(ср) ); Σ x 1 x n = Σ (X 1 -X 1(ср) )(X n -X n(ср) );

Σ x 1 y 1 = Σ (X 1 -X 1(ср) )(Y 1 -Y 1(ср) ); и т.д.

Характеристики гидратированных ионов

Таблица 1

Ион	Радиус иона, r_s ⋅ 10 - ⁸ см	Масса иона m_i	Гидратное число, n s	Масса гидратированного иона, m_s	Радиус гидратированного иона, r_s ⋅ 10 - ⁸ см	Энергия гидратации Е_s, кДж/моль (лит.)	Энергия гидратации Е s по ур.(5), кДж/моль
1	2	3	4	5	6	7	8
Li⁺	0,78	6,9	5,33	102,87	3,96	502	594,34
Na⁺	0,98	23	4,03	95,53	3,60	410	359,46
K⁺	1,33	39	2,69	87,52	3,15	329	350,04
Mg²⁺	0,78	24,3	11,70	234,90	5,14	1887	2051,83
Ca²⁺	1,06	40,0	8,33	190,00	4,59	1569	1555,92
Sr²⁺	1,20	87,6	7,24	217,92	4,38	1477	1252,17
Ba²⁺	1,38	137,3	6,16	248,18	4,15	1339	927,84
Zn²⁺	0,83	65,4	11,97	280,86	5,18	2130	2029,18
Al³⁺	0,57	27,0	25,11	478,93	6,63	4548	4545,93
Fe³⁺	0,67	55,8	21,20	437,68	6,27	-	4001,47
F^–	1,33	19,0	2,69	67,52	3,15	423	400,37
Cl^–	1,81	35,5	1,70	66,18	2,70	330	355,73
Br^–	1,96	79,9	1,49	106,80	2,59	296	309,25
SO 4 ^2-	1,47	96,0	5,72	198,94	4,05	-	991,07
OH^–	1,40	17,0	2,51	62,18	3,08	-	288,21
MnO₄^–	2,40	157	1,03	175,54	3,30	-	333,65
NO 3 ^-	1,89	62,0	1,59	90,62	2,64	-	288,16
Cr 2 O 7 ^2-	2,40	216	3,10	271,80	4,16	-	855,54

Отметим важный физический смысл коэффициентов в уравнениях ММУМ. Например, коэффициент b 1 в формуле (3) отвечает на вопрос, на сколько единиц в среднем изменяется Y 1 , если X 1 изменяется на одну единицу в предположении, что X 2 при этом сохраняет постоянное значение.

Таким образом, формулы ММУМ позволяют исключить влияние фактора X 2 , корреляционно связанного с фактором X 1 на Y в чистом виде.

Данная идея положена в основу оценки энергий гидратации Е s различных ионов в виде уравнения (5) с соответствующим коэффициентом многоуровневого моделирования.

В таблице 1 также представлены литературные и оцененные величины Е s , систематические значения которых отсутствуют от таких базисных свойств, как радиус и масса иона, гидратное число, масса и радиус гидратированных ионов. Реализация компьютерной программы «ММУМ» [7] приводит к уравнению

Е s = 839,7192 ^. r i – 1299,3793 ^. m i – 23175,5342 ^. n s + 1296,3630^. m s + 410,2215 ^. r s - 2498,6900 (5) с коэффициентом МУМ, равным 0,9992. Приемлемость уравнения (5) к расчету энергий гидратации различных ионов, составляющих химические активаторы для упрочнения ИПВ, подтверждается высоким значением коэффициента МУМ ( К мум ), близким к 1,000. Этот коэффициент выражает тесноту связи между переменными в ММУМ, определяемый по формуле:

Кмум2 = Σ(Yi- Yср)2/Σ(yi - yср)2 , где yi – значения переменной Y, взятые из корреляционной таблицы 1 (колонка 7 – опорные значения), а Yi – значения переменной Y, вычисленные по ММУМ (колонка 8 – по уравнению 5).

Оцененные величины масс m s и энергий гидратации ионов Е s (колонки 5, 7 и 8 в табл. 1) дают возможность определения приведенных масс и энергий гидратации µ s и E s химических активаторов (добавок в ИПВ) (табл. 2).

Таблица 2

Влияние вида, количества и параметров добавок (химических активаторов) на предел прочности ИПВ, МПа

Химический активатор	CaSO 4 ∙2H 2 O	Ca(NO 3 ) 2	CaCl 2	CaF 2	Fe 2 (SO 4 ) 3 ∙9H 2 O	Na 2 SO 4	K 2 Cr 2 O 7	Al(OH) 3 (отходы Авиазавода)
Приведенная масса химического активатора, µ_s ( г/моль )	97,05	92,76	78,01	78,94	354,30	97,33	106,47	134,25
Приведенная энергия гидратации химического активатора , E s ( кДж/моль )	605,43	363,50	524,60	537,31	2196,15	448,73	406,65	831,07
Количество добавки мас.%	σ_пр, МПа (числитель – эксперимент, знаменатель – теория)
0	10,0	10,0	10,0	10,0	10,0	10,0	10,0	10,0
0,1	-	-	-	-	-	-	18,0	-
0,1	11,12⁶	15,34⁶	10,48⁶	10,32⁶	10,40⁶	14,22⁶	16,12⁶	11,11⁶
0,25	-	31,5	12,5	20,0	12,5	4,5	24,0	6,0
0,25	12,91⁷	20,93⁷	11,70⁷	11,43⁷	10,73⁷	18,78⁷	22,36⁷	12,75⁷
0,5	10,5	28,0	16,5	36,0	25,0	22,0	27,0	9,0
0,5	22,15⁸	25,26⁸	21,45⁸	21,36⁸	24,32⁸	24,47⁸	25,98⁸	20,27⁸
1,0	12,5	34,0	15,5	21,5	21,0	27,0	25,0	7,5
1,0	19,81⁹	24,80⁹	18,76⁹	18,61⁹	22,30⁹	23,52⁹	25,91⁹	20,28⁹
2,0	15,0	-	-	-	-	-	-	-
2,0	17,06¹⁰	26,23¹⁰	15,35¹⁰	15,06¹⁰	15,06¹⁰	23,83¹⁰	28,11¹⁰	17,52¹⁰
3,0	16,0	18,5	13,5	23,0	21,0	29,5	-	9,5
3,0	17,18¹¹	24,78¹¹	15,69¹¹	15,45¹¹	19,64¹¹	22,81¹¹	26,39¹¹	17,69¹¹
4,0	18,0	-	-	-	-	-	-	-
4,0	16,51¹²	19,82¹²	15,16¹²	15,09¹²	26,72¹²	19,08¹²	21,04¹²	18,06¹²
5,0	21,5	12,0	9,0	22,5	35,0	19,5	-	9,0
5,0	16,17¹³	15,08¹³	15,01¹³	15,10¹³	33,61¹³	15,60¹³	15,86¹³	18,67¹³
6,0	28,0	-	-	-	-	-	-	-
7,0	31,0	-	-	-	-	-	-	-
8,0	35,0	-	-	-	-	-	-	-

Примечание. 6, 7, 8, 9, 10, 11, 12 и 13 – номера уравнений, по которым рассчитаны пределы прочности σ пр , МПа (табл. 2).

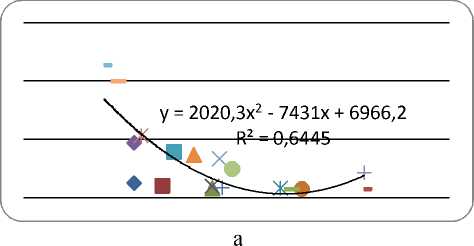
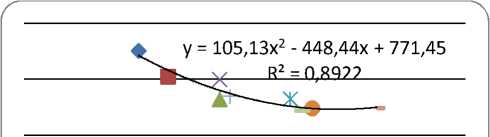
Другим способом оценки энергий гидратации ионов, входящих в состав химических добавок, является графическая зависимость Е s от собственных радиусов r s (рис. 1). Поскольку радиусы многих ионов известны и представлены в справочниках, по ним можно определить соответствующие энергии их взаимодействия с диполями воды (энергии гидратации). Рисунок 1 а соответствует зависимости для 1-, 2- и 3-зарядных, рис. 1 б –для 1-зарядных и 1 в – для 2-зарядных ионов.

В таблице 2 в числителе приведены экспериментальные значения предела прочности ИПВ σ пр , МПа [1]. Видно, что при добавках 0,1; 2,0 и 4,0% (мас.) опытные данные отсутствуют.

ММУМ позволяет теоретически оценивать пределы прочности ИПВ σ пр и рассчитать по уравнению

σпр = а µs + в Esприв + с пределы прочности для всех видов и количеств (до 5,0% мас.) химических активаторов с достаточно высокой вероятностью и надежностью (таблица 2 – знаменатель).

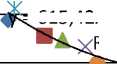
= 615,42x2 - 2697,3x + 3774,9 R² = 0,9249

Рис. 1. Взаимосвязь между радиусами ионов химических активаторов (ось абсцисс: r s ⋅ 10 - ⁸ см – колонка 1 табл. 1) их энергиями гидратации (ось ординат: Е s , кДж/моль – колонка 8 табл. 1):

а – для 1-, 2- и 3-зарядных ионов; б – для однозарядных ионов; в – для двухзарядных ионов

Таблица 3

Коэффициенты уравнения σ пр = а ^. µ s + в ^. E sприв + с

% добавки	№ уравнения	а	в	с
0,10	6	0,11790	-0,01952	11,50522
0,25	7	0,22088	-0,03709	13,92625
0,50	8	0,09878	-0,01461	21,40911
1,00	9	0,32804	-0,05174	19,00052
2,00	10	0,27135	-0,04271	16,59011
3,00	11	0,22899	-0,03549	16,44431
4,00	12	0,13964	-0,01616	12,74832
5,00	13	0,04497	0,00369	9,56743

В таблице 3 представлены коэффициенты уравнения

σ _пр = а µ_s + в E _sпр_ив + с для добавок от 0,1 до 5,0% (уравнения 6 – 13).

Анализ пределов прочности ИПВ в зависимости от количества и видов химических активаторов показывает, что некоторые экспериментальные величины имеют аномальные отклонения, что может быть объяснено, скорее всего, ошибкой опыта, а для Al(OH) 3 (отходы Авиазавода) наблюдается значительно меньший (по сравнению с другими активаторами и расчетными величинами) предел прочности, что может быть объяснено присутствием в отходах Авиазавода компонентов, ослабляющих прочность ИПВ.

Таким образом, ММУМ вполне приемлем к прогнозированию математическими методами пределов прочности ИПВ в зависимости от вида и количества химических активаторов.

Статья научная