Прогнозные модели реакции полимеризации этилена в системах обеспечения противоаварийной защиты и экологической безопасности

В настоящее время вопросам безопасности зоны реакции.

и экологии на производстве уделяется все большее внимание. Для производства полиэтилена объем выбросов в атмосферу или на факел относительно невелик, однако в связи с особенностями технологического режима периодически и достаточно часто необходим сброс давления в реакторе при достижении критической температуры. При этом не прореагировавшая газовая смесь, если не возникает аварийной ситуации, смешивается со свежим сырьем и повторно направляется в реактор. Подобная схема с рециклом имеет следующие недостатки: снижается выход продукта, повышаются затраты электроэнергии, повышается риск аварийных ситуаций [1].

Цель работы: разработка технических решений для системы мониторинга возможных аварийных ситуаций с использованием прогнозных моделей.

Задача разработки прогнозных моделей должна решаться для каждого из параметров работы трубчатого реактора полимеризации этилена (давление в реакторе, глубина сброса давления, период сброса давления, разность температур между 25 и 18 коленами реактора, разность температур между 29 и 14 коленами реактора). Выбор для исследования 14, 18, 25, 29 колен реактора обусловлен наличием трех зон в реакторе (нагрева, реакции и охлаждения), при этом указанные колена реактора находятся на границах

Результаты и обсуждение. Разностная модель для определения прогнозного ( i+1 – о) значения на примере давления в реакторе имеет следующий вид [2]:

n

Р прог = С 0 + Х С' P i " 1 , (1)

где Р прог – прогноз давления в реакторе, n – число данных архива, C i – коэффициенты модели, P i – давления в реакторе на i предыдущих шагов.

Коэффициенты модели рассчитывались с помощью метода наименьших квадратов (МНК). Расчет коэффициентов моделей проводился с помощью пакета программ SPSS Statistics 17.0 [3]. Оценка значимости уравнения регрессии для полученных моделей производилась на основе F-критерия Фишера, которому предшествовал дисперсионный анализ. В табл. 1 приведены значения, рассчитанные в ходе дисперсионного анализа для прогнозных моделей давления в реакторе, аналогичные расчеты проводились и для остальных параметров (глубина сброса давления, период сброса давления, разность температур между 25 и 18 коленами реактора, разность температур между 29 и 14 коленами реактора). По результатам анализа можно сделать вывод о том, что для всех рассматриваемых моделей значение F-критерия Фишера превосходит табличное, что свидетельствует об адекватности моделей.

Таблица 1. Дисперсионный анализ прогнозных моделей давления в реакторе для n от 1 до 5.

Модель		Сумма квадратов	Степень свободы	Средний квадрат	F-критерий
1	регрессия	2332,172	1	2332,172	402,447
	остаток	596,882	103	5,795
	всего	2929,054	104
2	регрессия	2349,218	2	1174,609	206,628
	остаток	579,836	102	5,685
	всего	2929,054	104
3	регрессия	2349,218	3	783,073	136,401
	остаток	579,836	101	5,741
	всего	2929,054	104
4	регрессия	2439,033	4	609,758	124,435
	остаток	490,021	100	4,900
	всего	2929,054	104
5	регрессия	2444,423	5	488,885	99,869
	остаток	484,631	99	4,895
	всего	2929,054	104

Для определения оптимального значения n был произведен расчет пяти прогнозных моделей для каждого из параметров реакции с числом ретроспективных шагов от 1 до 5. Для каждой из моделей определяли среднеквадратичную ошибку аппроксимации [4]:

ε =

yi

~ y мод

q - m

⋅100% yi     ,(2)

где q – число опытов, m – число параметров в уравнении регрессии, y i – реальное значение прогноза параметра, ^{~ y} мод – значение прогноза параметра, рассчитанное по модели. По результатам расчета (рис. 1) видно, что оптимальным значением n является 2.

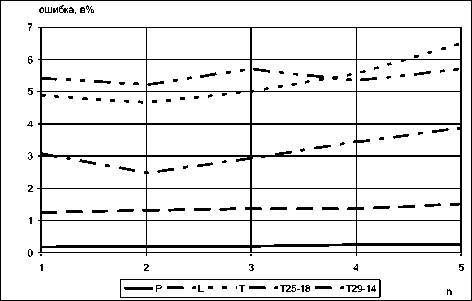
Рис. 1. Изменение среднеквадратичной ошибки аппроксимации прогнозных моделей для параметров реакции в зависимости от n

Оценку адекватности прогнозных моделей, кроме F-критерия Фишера, можно осуществлять с помощью t-критерия Стьюдента. Учитывая, что для моделей с n =2 степень свободы равна 102, то ближайшее значение t табл равно 1,982.

В табл. 2 приведены значения коэффициентов моделей и расчетные значения t-критерия Стьюдента. Полученные результаты позволяют сделать вывод о значимости всех коэффициентов для каждой из моделей, что в свою очередь означает о возможности х использования в качестве прогнозных. Для оценки точности прогноза по полученным моделям был произведен расчет прогнозных значений. Точность расчета по модели определяется с помощью (2), при этом критическим значением ошибки были выбраны 10%.

Таблица 2. Коэффициенты прогнозных моделей ( n =2)

Модель ( n =2)		Нестандартизо-ванные коэффициенты		t-критерий Стьюдента
		С	Станд. ошибка
P	С 0	167,362	68,164	2,455
	С 1	1,057	0,097	10,952
	С 2	-0,172	0,099	-2,032
dP	С 0	67,796	19,395	3,496
	С 1	0,895	0,098	9,095
	С 2	-0,117	0,099	-2,079
T	С 0	5,032	1,661	3,029
	С 1	1,271	0,091	13,917
	С 2	-0,383	0,091	-4,213
T 25-18	С 0	3,199	0,813	3,935
	С 1	1,151	0,093	12,417
	С 2	-0,357	0,094	-3,798
T 29-14	С 0	1,748	0,797	2,193
	С 1	1,541	0,081	19,141
	С 2	-0,579	0,080	-7,218

Примечание: С 0 , С 1 , С 2 – коэффициенты модели вида (1) для каждого из параметров реакции полимеризации

На рис. 2 приведены графики изменения среднеквадратичной ошибки аппроксимации. По полученным результатам видно, что при критическом значении средней ошибки аппроксимации (10%) горизонт прогноза равен трем шагам. Учитывая, что каждый шаг равен циклу работы реактора и в среднем составляет около минуты (период сброса давления, полученный по экспериментальным данным), то полученные модели позволяют прогнозировать работу реактора на три минуты. При оперативной реакции системы противоаварийной защиты (ПАЗ) или персонала вполне достаточно для внесения корректировок в управление процессом с целью предотвращения аварийных ситуаций и снижения затрат на производство.

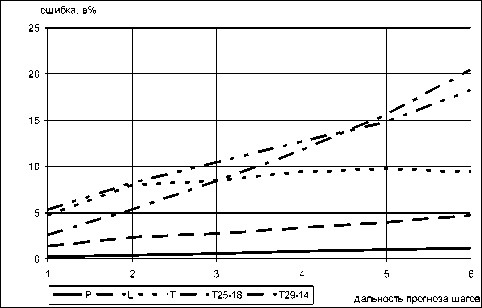
Рис. 2. Изменение среднеквадратичной ошибки аппроксимации прогнозных значений в зависимости от дальности (горизонта) прогноза

Для управления процессом с целью предотвращения аварийных ситуаций может быть разработана автоматизированная система, в основе которой используются полученные прогнозные модели и регулятор на основе нечеткой логики. Таким образом, в зависимости от приближения прогноза к критическим значениям выбирается интенсивность воздействия на процесс (при незначительных и долгосрочных приближениях используется возможности системы управления, при критических приближениях – системы ПАЗ).

Выводы:

• 1.    Разработанные модели с достаточной точностью (погрешность не более 10%) позволяют прогнозировать параметры реакции полимеризации этилена на три цикла реакции, что в среднем равно трем минутам.

• 2.    Предложенная система прогнозирования может быть интегрирована в существующую систему АСУ ТП для обеспечения безопасности и уменьшения вредных выбросов в процессе производства.

• 3.    Предложенные прогнозные модели параметров реакции полимеризации этилена могут быть использованы для разработки автоматической системы предотвращения аварийных ситуаций.