Программа электромагнитного моделирования антенных решеток КВ-диапазона

анализируемой области; 4) перечнем параметров, подлежащих анализу или входящих в состав критерия синтеза АР; 5) стоимостью лицензий на программный продукт; 6) набором и особенностями численных методов, которые реализованы в ПП; 7) аппаратными требованиями программного обеспечения и пр. Главным образом качество решения задачи выбора определяется особенностями моделируемой (анализируемой и синтезируемой) АР, которые с учетом классических задач и типовых математических моделей электродинамики [4] взаимоувязываются с методами вычислительной электродинамики [5]. Принимая во внимание геометрические особенности АР КВ-диапазона из указанного перечня ПП и критериев выбора MMANA GAL и 4nec2, учитывают тонкопроволочные приближения [6], которые при неизменной адекватности формируемой математической модели позволяют существенным образом снизить вычислительные затраты при решении задач анализа и синтеза антенной системы. Однако применение ПП MMANA GAL и 4nec2 в решении задач электромагнитного моделирования АР КВ-диапазона связано со следующими ограничениями: 1) на число параметров моделируемой АР: проводники – м аксимум 5 12 для базовых версий lm^^m © Полянский И.С. и др., 2019

и 10000 для лицензионных; сегменты (тонкопроволочные структуры – ТПС), на которые разбивается проводник при сведении формируемой системы сингулярных интегральных уравнений (СИУ) к системе линейных алгебраических уравнений, – максимум 8192 для базовых версий и 45000 для лицензионных; источники – максимум 64 для базовых версий и 300 для лицензионных; объединяемых файлов (объединение отдельных антенн в АР) – 4 для лицензионных версий; 2) вычисления реализуются в один поток без распараллеливания задач на многопроцессорных системах CPU и/или графических ускорителях GPU.

Указанные особенности ПП обуславливают их непригодность и неспособность эффективного решения задач анализа и синтеза многоэлементных АР КВ-диапазона, что определило необходимость разработки методики электромагнитного моделирования многоэлементных АР КВ-диапазона и ее программной реализации при использовании технологий параллельных вычислений.

Методика разработана при выборе следующей системы ограничений и допущений:

• 1)    проводник представляется цилиндрическим с диаметром, много меньшим в сравнении с длиной волны;

• 2)    распределение тангенциального поля и тока на поверхности проводника определяется только продольными составляющими, которые параллельны оси проводника;

• 3)    поперечная вариация поля и тока не учитывается при описании зависимостей соответствующих функций одной переменной – криволинейная координата, отсчитываемая вдоль оси проводника;

• 4)    среда является однородной и изотропной, а векторы электромагнитного поля меняются во времени по гармоническому закону с угловой частотой to = 2 п c о /X ( c о = 299792458 м/с - скорость света в вакууме);

• 5)    влияние поверхности Земли на электромагнитное поле (ЭМП) АР КВ-диапазона определяется в приближении метода электрических изображений;

• 6)    граничные условия относительно проводника и среды распространения определяются граничными условиями Леонтовича [5] – на поверхности раздела диэлектрика и металла с конечной электропроводимостью.

С учетом заданной системы ограничений и допущений сформулируем содержательную постановку задачи анализа АР КВ-диапазона в следующем виде. Основные объекты АР - N е N ан тенн, M е N источников передающего устройства (ИПрдУ) и M'е N нагрузок. Каждая n-я антенна

( n = 1, N ) состоит из K n е N элементов. Каждый

( k n = 1,K _n ) представляется линейным

k_n элемент

отрезком с параметрами: положение начальной точки Pbn = (xbn ,ykn ,zkn);

положение конечной

— e e e e точки Pkn = ( xk ,yk ,zk I; радиус ik; удельное со- противление ницаемость

металла Z^s k_n

p k ; относительная магнитная про- ц k ; поверхностное сопротивление = ( 1 + i ) 0,5 ®Ц 0 Ц _k n Р _k n , где i = V—1;

Цо = 4п-10 7 Гн/м - магнитная постоянная. Пара- метризация элементов задана в следующем виде:

*

L k_n

— e kn

^—          —     -— b

^L k_n ⁽ t ) = e k_n t ^{+ Pk} n , t ^е[ ^0,1 ]

-— e

P k_n

—

-— _b

P k_n

Каждый m-й ИПрдУ (m = 1,M) и m' -я нагрузка (m' = 1,M') представляются точечными с па- раметрами: номер kn элемента антенны из АР

-—b при выборе размещения в одной из точек Pkn ,

• 7 ^—    b ^— e ^         ^-— e

0,51 Pkn + Pkn I или Pkn - в начале, посередине или в конце. Для точечного ИПрдУ также указываются амплитуда Umm и фаза уm входного напряжения Um = UmmeiYm; входное сопротивление

J?mx = Rm + iXm, задаваемое активной Rm и реак тивной X^^ составляющими.

Среда распространения V определяется следующими параметрами: абсолютной магнитной проницаемостью цa = ЦЦ0 с заданным значением относительной магнитной проницаемости ц; аб солютной диэлектрической проводимостю б a = ББ0 с заданным значением относительной диэлектрической проводимости б (б0 = 1jЦ0c2 - электрическая постоянная); в = ю^бaцa - волновое число; Wa = VЦa/aa - волновое число.

Подстилающая поверхность определяется относительными диэлектрической и магнитной про-ницаемостями, а также удельной проводимостью, задаваемой в мСм/м.

Основу методики электромагнитного моделирования многоэлементных АР КВ-диапазона составляет численное решение системы сингулярных интегральных уравнений (ССИУ) типа уравнения Поклингтона:

E 0 . ( t ) =

I e k- ^N Kv 1 Г

= ., XX i J ]»» a ( ^Т . ) G k , k, ⁽ • , t ' ) -       (2)

n '= 1 k . ' = 1 0 ^

- ZsГЛ1—I 5 Gk",kn (t’ ") IJk' (t')dt k"   "a Mhk.     5t5t"'

D ¹ .' k . ⁼ i »» a ^(T k . ^Т k . ) ЫК| ^X

x JJ G ( t , t ' ) v k . ( t ) v k ( t ' ) dt'dt ;

00    nn

(4б)

где E ° ( L^ ‘ ) - функция

распределения сторонне

го тангенциального поля на k ' , -м элементе; Тк ■ = "                      ^k "

= е^,, ^e k , | - направляющий орт вектора k " ,-го элемента; G_k . , _к,"_ ( t ^, t' ) = e i ^{Pp k} " - k" '( t ^, t Ур k . , k ., ( t ^, t ' ) ^-

D)21 l,l, = —— [ f-vk (t)vL (t')dtdt;(4в)

k.,k.-   toeJJ   dtdt   kk() k.()’ a00

bk‘, l ,k; = i;Z s Ie    efc| ffvk (t )vk- (t') dt'dt,(4г)

k., k.'       k.          .        k.

функция Грина; J k ( t' ) ность тока на k " ■ -м = ^€ ⁺ I L k . ⁽ t ^{) -} L k " ⁽ t' )| .

- неизвестная плот-элементе; р k k' ( t , t ' ) =

Следует отметить, что при сведении ССИУ к СЛАУ интегралы в (4) для заданного разложения J k ( t' ) вычисляются численно по методу Гаусса по M узловым точкам при разделении интервала интегрирования [ 0,1 ] на H i подынтервалов

h^l k_n

-

^A k . , h k . ^+A k .

для соответствующих базис-

Решение ССИУ (2) в разрабатываемой методике выполняется с применением проекционного метода Галеркина при задании разложения искомой

функции

в базисе (КЛБФ):

H_k - 1 n ll плотности тока J k ( t ) = X C k V k ( t ) .          l = 0      . .

кусочно-линейных базисных функций

ных функций. С целью снижения вычислительных затрат с учетом особенностей вычисления базисных функций v k . ( t ) суммирование при численном интегрировании осуществляется на интервал

k n

■ l , i n

h^l k_n

-

Ak , k_n

h^l k_n

+ Al k_n

во всех остальных слу-

V

l k n

- -( h k . - t )A.

если h l -At <  t <  h l ; k_nk n          k_n

⁽ t H^{1 -} ( t ^- h k . )/ ^A k . ^,

если h l <  t <  h l + At. ; k_nk_nk n

0, в противном случае,

и последующем сведении ССИУ к системе линейных алгебраических уравнений (СЛАУ):

F = C (1 D ¹ - D ² - D ³ ) .                                (3)

чаях значение под знаком суммы приравнивается к нулевому. Для устранения особенностей (сингулярности) в случаях . = . ' , k . = k . ,, | / - 1' | <  2 для регуляризации решения используются следующие преставления по разложению в ряд Тейлора:

- функции G ( t , t' ) :

^G k . , k . ,⁽ t , t ) = G ⁰ . , k . ,⁽ t , t ' ^{) +} G ⁵ k . , k . ,⁽ t , t ) ^;

G ⁰ . , k . .( t ^, t ) =Ур k . , k . , ( t ^, t ) ^- i e ;                             ⁽⁵⁾

/ л        (- i p) /        / ,\\k ^{- 1}

G ⁵ k . , k . .⁽ t , t ⁾ = X-^^{L (}v ^p k . , k . ' ⁽ t , t ) ) .

• k = 2 k •

• – функции GU-A M'W^{2 G} k . , k ; ( t ^, t l/s t a f-.

В заданных соотношениях приняты следующие обозначения: ^A k . = У ⁽ H k . - 1)^; H k . = [ H |e k J/1] ^; H - число базисных функций на ТПС длиной X ; h k. = к /( H k. - 1 ) ; * k„ = °, H k. - 1; ^F "  C ^- блочные векторы, состоящие из элементов F l и C l , k_.       k_.

соответственно; D 1 , D ² и D ³ - блочные матрицы,

G " ( t , t' ) =

+ в

-

—►

X e k_n

1. ll'          2

состоящие из элементов D ^{, ,} , D ^{, ,} k „, k ',’       k , k ',

соответственно;

и D3,l,l k., k.

FI = К I Ы ( t ) E_k * ( t ) dt ;

k_n n      k_nk_n

(4а)

-G t t l t - ) ^ ^[ e k . e k . ^{( 1 +} R ⁽ * , * ' ^{)) + (} R ⁽ t , t ) )

3         3 i )

-

( R ( t , t ) ) 2 R ⁽ t , t )_?

^{( L} k . ⁽ t ^{) - L} k . X t ' ) ) ⁵ k ., ⁽ L

= G "⁰ ( t , t' ) + (5' ' ( t , t' ) ;

X

G'0 (t, t ’ ) = ekek -,x k.,k.'. .

'        1                 в2

X ----------7 +----^-4

(ptt'(t,f))3 2pk.*(',">

V\ k., k.       )у

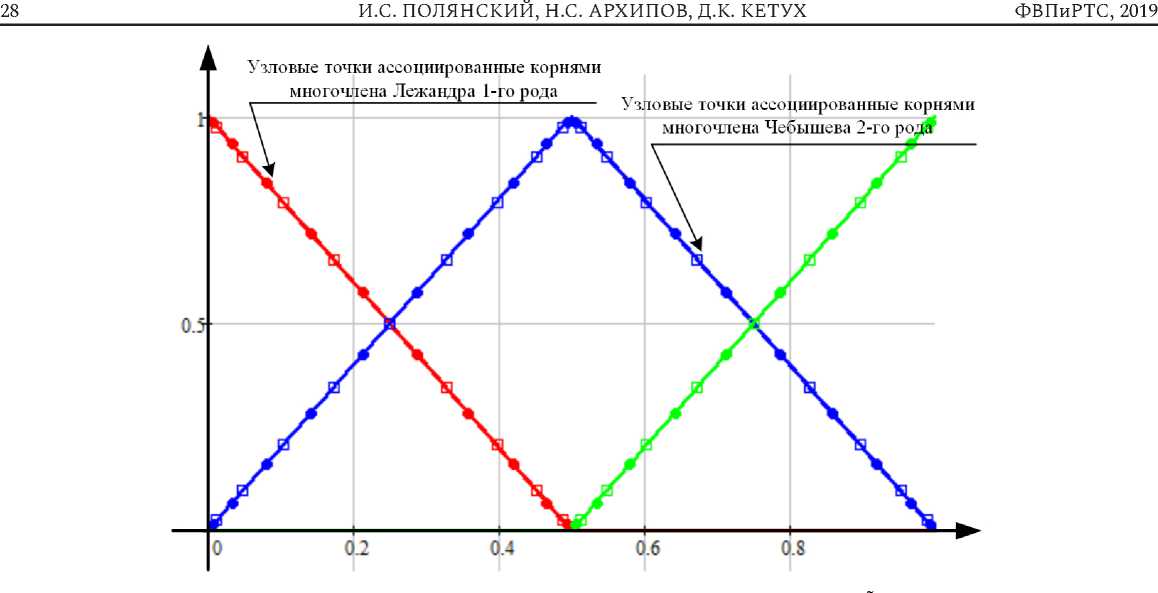
Рис. 1. Пример распределения точек (узлов) интегрирования КЛБФ на k n -м ТПС при H = 3, M = 10

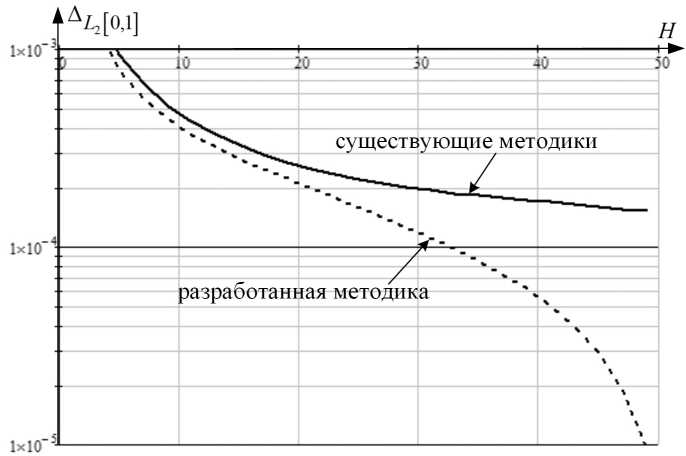
Рис. 2. Сравнительная зависимость сходимости в пространстве функций L 2 [ 0,1 ] предложенной методики от размерности формируемой СЛАУ

3          , в2

I <   Й 4 ⁺ I /   Й²

Ц₽ k n , k n ⁽ t , t ' ) )      ² ( ^P k n , k n ⁽ t , t ' ) )

в ⁴

X

e k ⁽ L k n ⁽ t ^{) -} L k n ’ ⁽ t ')) ⁵ k n ’ ( L k n ⁽ t ^{) -} L k n ⁽ t ')) . ^p v;, ⁽ t , t ')                  ’

G L k ;, .( t , t ^,)= i P 5 L k , ⁽ t ^{) -} Ldt ) ^{2 X}

” (k + 2) (k + 4                  k i1 c,(--pkn, kn( t , t >в) - k=0

- в Е^—₽ц4^.

i = i ( k + 1 ) ! ( k + 3 )

Для заданных представлений в случаях n = n', k-n = knч | — l'|- 2 численное интегрирование по точкам наблюдения t' по методу Гаусса выполня ется для ЪЛ узловых точек, являющихся корнями многочлена Лежандра первого рода степени Л4. Численное интегрирование по точкам источника t по методу Гаусса выполняется для Л4 -1 узловых точек, являющихся корнями многочлена Чебышева второго рода степени Л4 -1. Пример распределения точек интегрирования на КЛБФ при M = 10 представлен на рис. 1.

Следует отметить, что элементы вектора F (вектор граничных условия), вычисляемые по правилу (4а), задают условия возбуждения АР электрическим полем. Модель возбуждения m -м точечным источником предполагает разделение соответствующего k_n -го ТПС на две части бесконечно узким зазором с приложением к последнему напряжения U m = U m e ^Y m . Краевое поле на зазоре при таком подключении не учитывается.

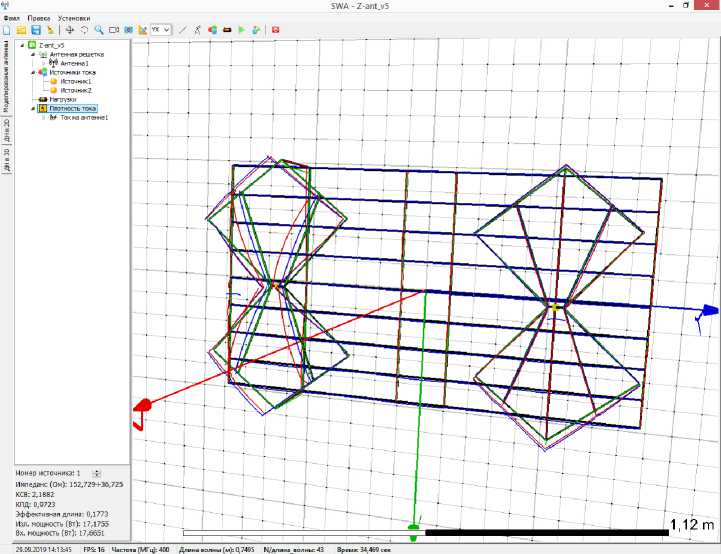
Рис. 3. Интерфейс программы электромагнитного моделирования АР КВ-диапазона

Плоскость YX

(•) Свободное пространство

О Электрическая стенка

О Магнитная стенка

О Почва

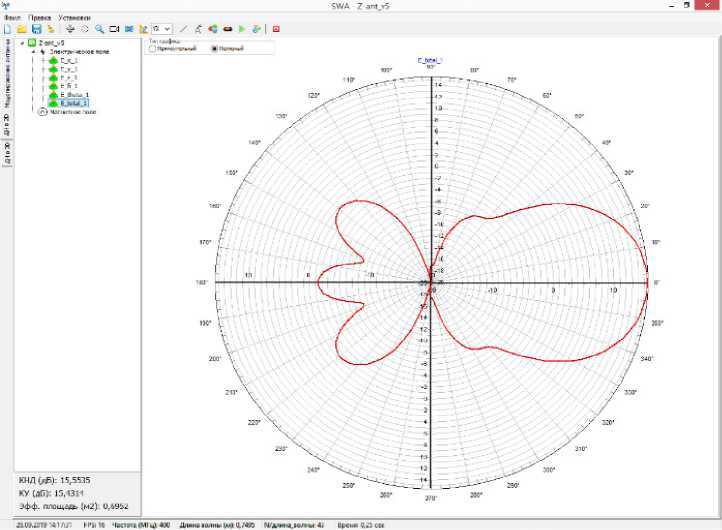
Рис. 4. Примеры расчета ДН АР КВ-диапазона

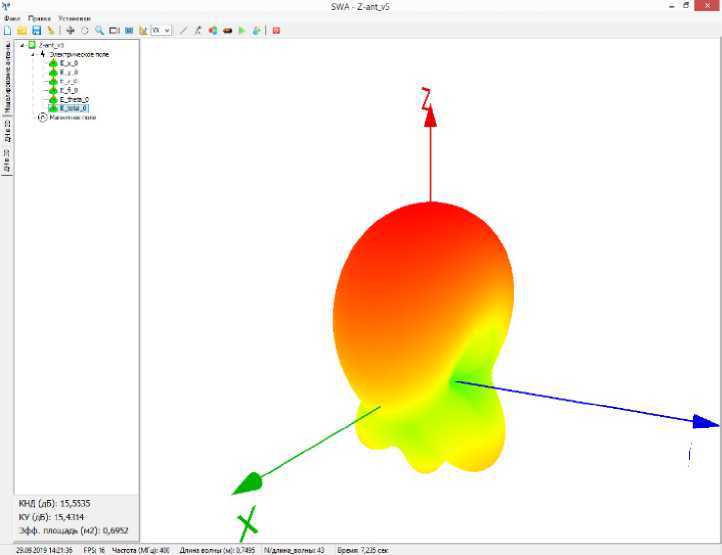
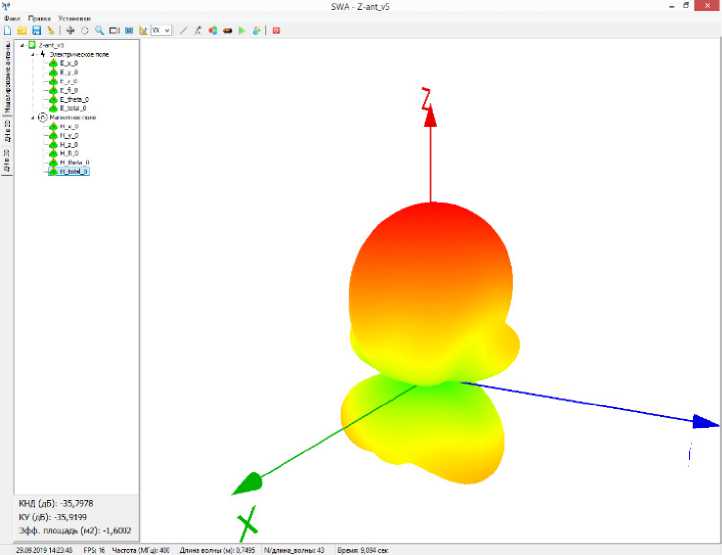
Окончание. Рис. 4. Примеры расчета ДН АР КВ-диапазона

Результаты апостериорной оценки зависимости сходимости предложенного решения от размерности формируемой СЛАУ в сравнении с методом коллокаций, реализованным в MMANA GAL и 4nec2, при анализе АР из трех по л уволновых вибраторов представлены на рис. 2.

По сформированной методике разработана программа электромагнитного моделирования АР КВ-диапазона, интерфейс которой приведен на рис. 3.

С учетом выделенных особенностей методики программа позволяет выполнять расчет: 1) распределения токов на ТПС; 2) электромагнитных параметров АР относительно ИПрдУ – импеданс, КСВ, КПД, эффективную длину и площадь, излучаемую и входную мощности; 2) трехмерную и в заданной плоскости сечения диаграммы направленности (ДН) антенны по напряженности электрического и магнитного полей с учетом подстилающей поверхности (рис. 4); 3) интегральные характеристи-

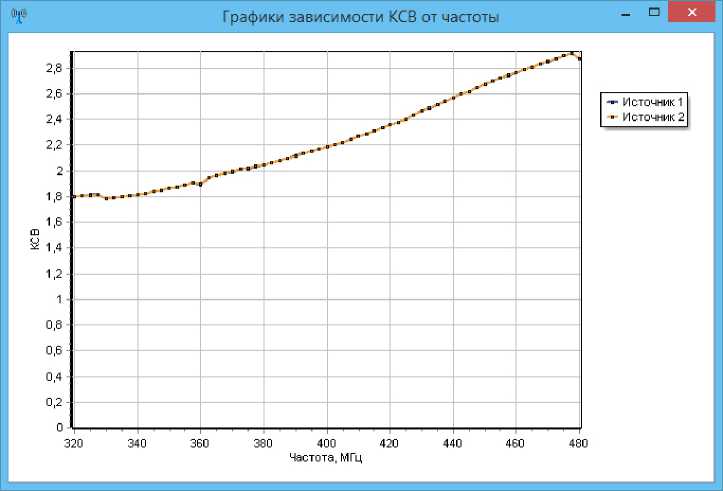
Рис. 5. Примеры расчета графика зависимости КСВ ИПрдУ от частоты

ки направленности АР – КНД и КУ; 4) расчет зависимости КСВ ИПрдУ от частоты (рис. 5); 5) подбор амплитуд и фаз ИПрдУ для реализации требуемых характеристик направленности.

В целом сформированные решения позволили без введения ограничений на размер и число эле- ментов в анализируемой АР при распараллеливании вычислительных процессов при численном интегрировании (суммировании) на CPU реализовать вычислительные процедуры анализа и синтеза АР КВ-диапазона в режиме времени, близком к реальному.