Программная реализация математической модели кинематического расчета плоских рычажных механизмов

Проектирование механизма представляет собой сложную инженерную задачу, решая которую приходится определять оптимальную кинематическую схему механизма на основе технического задания. Решение задачи анализа облегчается при визуализации кинематики рассматриваемого механизма. Поэтому программная реализация математической модели кинематического расчёта плоских рычажных механизмов представляет интерес [1–6].

В качестве языка программирования был выбран Turbo Pascal фирмы Borland – базовый язык программирования в учебных заведениях.

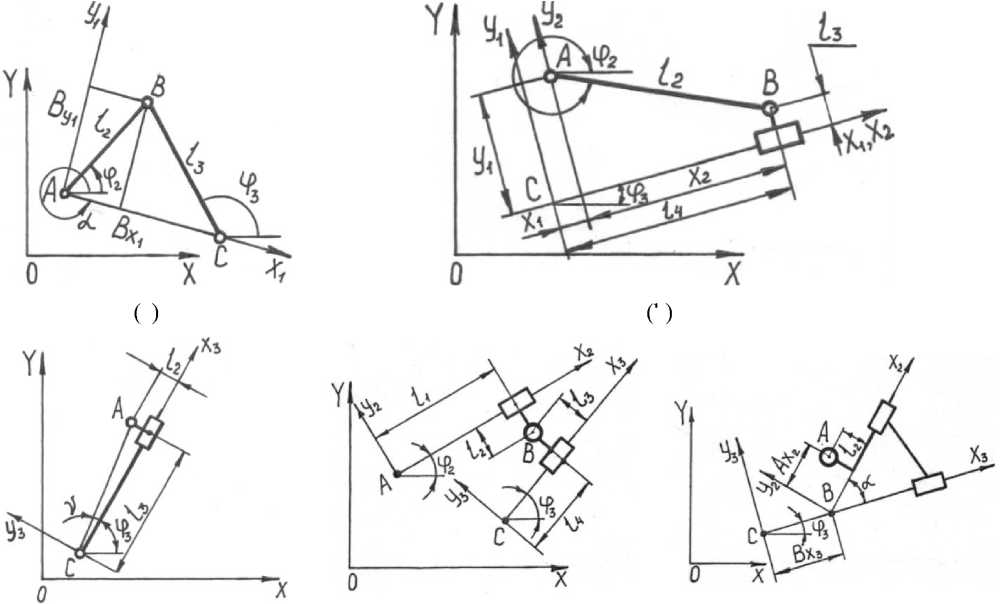
По результатам работ [1–2] разработаны компьютерные процедуры, вычисляющие кинематических характеристики любых плоских рычажных механизмов, имеющих в своём составе, кроме начального звена, хотя бы одну двухповодковую группу Ассура. Расчётные схемы показаны на рисунке 1.

На рисунке 1 приняты следующие обозначения: l 2 , l 3 – размеры второго и третьего звеньев; l 4 , l 5 – вспомогательные размеры; φ 2 , φ 3 – углы наклона к оси абсцисс второго и третьего звеньев; α, γ – вспомогательные углы.

На языке Turbo Pascal составлен модуль DIADA. В этот модуль входят библиотечные процедуры, определяющие кинематические характеристики каждой двухповодковой группы Ассура.

Листинг модуля DIADA

Unit Diada;

Interface

Var al1,al2,a21,a22,calpha,salpha: real; bl,b2,alpha,znam : real;

bx,by : real;

ch : char;

Procedure Di- ada2v(ax,ay,vax,vay,aax,aay,cx,cy, vcx,vcy,acx,acy,fi3,omega3,epsi3,12,13:re al;

Var fi2,omega2,epsi2,14,v4,a4:real); Procedure Di- ada3v(ax,ay,vax,vay,aax,aay, cx,cy,vcx,vcy,acx,acy,12: real;

Var fi3,omega3,epsi3,13,v3,a3: real); Procedure Di-ada4v(ax,ay,vax,vay,aax,aay,fi2, omega2,epsi2,cx,cy,vcx,vcy,acx,acy,fi3,om ega3, epsi3,12,13: real; Var ll,vl,al,14,v4,a4: real);

Procedure Di- ada5v(ax,ay,vax,vay,aax,aay,cx, cy,vcx,vcy,acx,acy,12,fi3,omega3,epsi3,al pha: real;

VarAx2,Vax2,Aax2,Bx3,Vbx3,Abx3: real);

Function Atan2(x,y: real): real; Implementation Function Atan2;

Begin if (x > 0) and (y >= 0) then Atan2:=ArcTan(y/x);

if (x > 0) and (y <= 0) then Atan2:=2*pi-ArcTan(abs(y)/x);

if (x < 0) and (y >= 0) then Alan2:=pi-ArcTan(y/abs(x));

if (x < 0) and (y <= 0) then Alan2:=pi+ ArcTan(y/x);

if (x = 0) and (y > 0) then Atan2 := pi/2;

if (x = 0) and (y < 0) then Atan2 := 3*pi/2

End;

Procedure Diadalv;

Var ac,bxl,byl,bx,by : real;

Begin {Diadalv} ac:= sqrt(sqr(cx - ax) + sqr(cy - ay));

alpha:= Atan2(cx – ax, cy - ay); salpha:= sin(alpha); calpha:= cos(alpha); bxl:= (sqr(12) + sqr(ac) -sqr(13))/(2*ac);

byl:= sqrt(sqr(12) - sqr(bxl));

ifsb = 2thcnbyl :=-byl;

bx:= ax + bx1*calpha - by1*salpha;

by:= ay + bxl*salpha + by1*calpha;

fi2 := Atan2(bx - ax,by - ay); if fi2 > 2*pi then fi2 := fi2 -2*pi;

fi3 := Atan2(bx – cx,by - cy); if fi3 > 2*pi then fi3 := fi3 -2*pi;

if fi2< 0 then fi2 := fi2 + 2*pi;

if fi3< 0 then fi3 := fi3 + 2*pi;

all :=-12*sin(fi2);al2:= 13*sin(fi3);

a21:= 12*cos(fi2);  a22 := -

13*cos(fi3);

znam :=all*a22-a21*al2;

bl := vcx - vax; b2 := vcy - vay;

omega2 := (b1*а22 - b2*а12)/znam;

omega3 := (a11*b2 - а21*b1)/znam;

bl := acx - aax + a21*sqr(omega2) + a22*sqr(omega3);

b2 := асу - aay - al l*sqr(omega2) -al2*sqr(omega3); epsi2 :=(b1*a22-b2*a12)/znam; epsi3 :=(a11*b2-a21*b1)/znam;

End; {Diadalv}

(a)

(b)

(c)

(d)

(e)

Рисунок 1. Расчётные схемы двух поводковых групп Ассура: a – первого вида; b – второго вида; c – третьего вида; d – четвёртого вида; e – пятого вида

• Figure 1.    Settlement schemes of two flood groups of Assur: a – first look; b – second look; c – third look; d – fourth look; e – fifth look

Procedure Diada2v;

Var xl,yl,x2,bx,by: real; Begin {Diada2v} b1:= ax-cx; b2:=ay-cy; xl :=b1*cos(fi3) +b2*sin(fi3); yl :=b2*cos(fi3)-b1*sin(fi3);

x2:=sqrt(sqr(12)-sqr(yl-l3)); 14:=xl +x2;

bx := cx +14*cos(fi3) - l3*sin(fi3); by := cy + l4*sin(fi3)+l3*cos(fi3); fi2 := Atan2(bx - ax,by - ay);

a11:= -12*sin(fi2); a12 := - cos(fi3);

a21:= 12*cos(fi2); a22 := - sin(fi3); znam :=all*a22-a21*al2;

bl := vcx - vax + omega3*(14*a22 + 13*a12);

b2 := vcy - vay - omega3*(14*a12 -13*a22);

omega2 := (bl*a22 - b2*al2)/znam; v4:=(all*b2-a21*bl)/znam;

bl =acx -aax - (14*cos(fi3) -13*sin(fi3))*sqr(omega3);

bl:=bl +12*cos(fi2)*sqr(omega2); bl:= bl - 2*v4*sin(fi3)*omega3 -epsi3*(l4*sin(fi3) +13*cos(fi3));

b2:= асу - aay - (14*sin(fi3)

+13*cos(fi3))*sqr(omega3);

b2:= b2 + 12*sin(fi2)*sqr(omega2);

b2:= b2 + 2*v4*cos(fi3)*omega3

+epsi3*(14*cos(fi3)-13*sin(fi3));

epsi2:= (bl*a22 - b2*al2)/znam;

a4:= (al 1 *b2 - a21 *bl)/ znam;

End; {Diada2v}

Procedure Diada3v;

Begin {Diada3v }

13 := sqrt(sqr(ax - cx) + sqr(ay - cy) -sqr(12));

a11:= cos(fi3); al2 := - (13*sin(fi3) + 12*cos(fi3));

a21 := sin(fi3); a22 :=13*cos(fi3) -

12*sin(fi3);

znam:=all*a22-a21*al2;

b1:= vax - vcx; b2 := vay - vcy;

v3 := (b1*a22 - b2*а12)/znam;

omega3 := (a11*b2 - a21*b1)/znam;

bl:= aax - acx + 2*v3*a21*omega3 + a22*sqr(omega3);

b2:= aay - асу - 2*v3*all*omega3 -al2*sqr(omega3);

a3:=(bl*a22-b2*al2)/znam;

epsi3 := (a11*b2 - a21*b1 )/znam;

End; {Diada3v }

Procedure Diada4v;

Begin {Diada4v } a11:= cos(fi2); a12:= - cos(fi3);

a21:= sin(fi2); a22:= - sin(fi3);

znam := a1l*a22 - a21*al2;

b1:= cx - ах+12*а21 + 13*а22;

b2:=cy-ay-12*a11 -13*а12;

I1:=(b*a22-b2*a12)/znam;

14:= (a11*b2 -a21*b1 )/znam;

bl:=vcx- vax+omega2*(ll*a21+I2*a11)+omega3*(14*a22 +13*а12);

b2:=vcy-vay-omega2*(ll*a11-12*a21) – omega3*(14*al2 -13*a22);

vl :=(b1*a22-b2*al2)/znam;

v4:=(all*b2-a21*b1)/znam;

bl:= acx - aax

+2*v1*a21*omega2+sqr(omega2)*(l1*a11-

12*a21)+ epsi2*(ll*a21 -12*all);

bl:=bl + 2*v4*a22*omega3 + sqr(omega3)*(14*al2-13*a22)+ epsi3*(14*a22 + 13*al2);

b2:= асу- aay-2*vl*al l*omega2 + sqr(omega2)*(ll*a21 + 12*al1)-epsi2*(ll*all -l2*a21);

b2:= b2-2*v4*al2*omega3+ sqr(omega3)*(14*a22 + 13*al2)- epsi3*(14*al2-13*a22);

al :=(bl*a22-b2*al2)/znam;

a4:= (a11*b2-a21*b1 )/znam;

End; {Diada4v }

Procedure Diada5v;

Begin {Diada5v } a11:= cos(fi3); al2:= cos(fi3 + alpha);

a21:= sin(fi3); a22:= sin(fi3 + alpha);

znam:=all*a22-a21*al2;

bl:= ax-cx+12*a22;

b2:=ay-cy-12*al2;

Bx3:=(bl*a22-b2*al2)/znam;

Ax2:=(all*b2-a21*bl)/znam;

bl:= vax-vex+omega3*(Bx3*a21 + Ax2*a22 + 12*al2);

b2:=vay-vcy- omega3*(Bx3*al 1 + Ax2*al2 – 12*a22);

Vbx3 :=(bl*a22 - b2*al2)/znam;

Vax2 := (a11*b2 - a21 *bl)/znam;

bl := aax - acx + 2*omega3*(Vbx3*a21 +

Vax2*a22) + sqr(omega3)*(Bx3*a11 + Ax2*al2 - 12*a22)

+ epsi3*(Bx3*a21 + Ax2*a22 + 12*al2);

b2:= aay - асу - 2*omega3*(Vbx3*al 1 +

Vax2*al2)+ sqr(omega3)*(Bx3*a21 + Ax2*a22 + 12*al2) – epsi3*(Bx3*a11 + Ax2*a12 -12*a22);

Abx3 :=(bl*a22 - b2*a12)/znam;

Aax2 := (a11*b2 - a21*bl)/znam;

End; {Diada5v}

End. { UnitDiada }

Определение кинематических характеристик механизма и построение его положений, планов скоростей и планов ускорений проведём на примере шестизвенного механизма (рисунок 2). Начало неподвижной координатной системы совпадает с осью вращения кривошипа АВ (звено 1). Предполагается, что известны длины всех звеньев, координаты всех дополнительных точек звеньев и координаты всех кинематических пар стойки механизма (звено 0), т. е. данному этапу работы по определению кинематики механизма должен предшествовать этап синтеза механизма (определение недостающих размеров звеньев).

Задаём координаты точки С и учитывая, что аналоги скоростей и ускорений этой точки равны 0 (точка неподвижна), обращаемся к процедуре, вычисляющей кинематику группы Ассура третьего вида diada3v.

Указываем кинематические характеристики точки D, принимая начало направляющей ползуна Е в точке С, угол наклона, аналог угловой скорости и аналог углового ускорения направляющей равными нулю, зная длину шатуна DE (звено 4) и длину звена 5, обращаемся к процедуре для группы Ассура второго вида diada2v.

Таким образом, для положения начального звена определены все кинематические характеристики механизма. Как уже отмечалось, вывод полученных результатов кинематического анализа нагляднее всего представить графически.

Листинг программы анализа кинематики шестизвенного механизма приведён далее.

Program Example;

Uses diada,crt,graph;

Label start;

Const nc = 360;

Var ij,d,r,ox,oy,pvx,pvy,pax,pay, xl,yl,x2,y2,kl,kv, ka:integer;

Il,130,14,lcd,cx,cy,fil,fi3,fi4,oml,om3,o m4,epsi3,epsi4 :real;

15,v5,a5,bx,by,dx,dy,cx,vbx,vby,abx,aby,v dx,vdy,adx,ady : real;

13,v3,a3,lcb : real;

ch : char;

stl,st2,st3,st4 : string;

Procedure Postpara(x,y: integer; fi: real);

Var zl,z2,z3,z4,z5,z6 : integer; wl,w2,w3,w4,w5,w6 : integer; sfi,cfi: real;

begin sfi := sin(fi); cfi:= cos(fi);

zl := x + round(10*cfi - 5*sfi);wl:= у -round(10*sfi+5*cfi);

z2 := x+round(-10*cfi-5*sfi); w2:= у -round(-10*sfi+5*cfi);

z3:= x + round(-10*cfi + 5*sfi);w3:=у-round(-10*sfi-5*cfi);

z4 := x + round(10*cfi + 5*sfi); w4:=у-round(10*sfi - 5*cfi);

z5:= x - round(10*cfi); w5 := у + round(10*sfi);

z6:= x + round(10*cfi); w6 := у -round(10*sfi);

SetColor(lightgray);

Setlinestyle(0,0,3); Iine(z5,w5,z6,w6);

SetColor(white); Setlinestyle(0,0,1); Line(z1,wl,z2,w2); line(z2,w2,z3,w3);

line(z3,w3,z4,w4); line(z4,w4,z1,wl);

circle(x,y,3);

end; {Postpara}

Procedure Opora(x,y: integer);

Begin circle(x,y,3);

Lineto(x - 7,y + 7); Lineto(x - 9,y + 7); lineto(x + 9,y + 7); lineto(x + 7,y + 7); lineto(x,y);

SetFillStyle(l,GetColor);

Bar(x - 9,y + 7,x + 9,y + 10);

End;

ProcedureCoordXY(x,y: integer);

Begin

SetColor(magenta);

line(x - 10,y,x + 100,y); line(x + 100,y,x + 90,y - 5);

line(x + 100,y,x + 90,y + 5);

OutTextXY(x + 105,y - 7,'X'); line(x,y + 10,x,y - 100);

line(x,y - 100,x - 5,у - 90); line(x,y - 100,x + 5,y - 90); OutTextXY(x + 5,y - 107,'Y'); SetColor(white);

End;

Begin clrscr;

11 := 0.3; 130 := 1.4; lcd := 0.5; 14 := 1.25;

cx :=0.0; cy := - 1.0;ox := 100; oy := 200;

kl :=150;kv :=350; ka := 350;

pvx := 450; pvy := 125; pax := 450; pay := 275;

d := Detect;InitGraph(d,r, '...\bgi'); SetBkColor(lightgray);

start: for i := 0 to nc do begin setfillstyle(9,green);

bar(20,380,620,455);

fi1 := 2*pi/nc*i;

bx :=ll*cos(fil);

by :=ll*sin(fil);

vbx:=-by; {-ll*sin(fil);} vby :=bx; {11*cos(fil);} abx:=-bx; {-11 *cos(fil);} aby:=-by; {-ll*sin(fil);} diada3

v(bx,by,vbx,vby,abx,aby,cx,cy,0,0,0,0,0,f i3,om3,epsi3, lcb,v3 ,a3);

dx := lcd*cos(fi3); dy := cy + lcd*sin(fi3);

vdx:=lcd*sin(fi3)*om3;

vdy:=lcd*cos(fi3)*om3;

adx := - lcd*(cos(fi3)*sqr(om3) + sin(fi3)*epsi3);

ady := lcd*(cos(fi3)*epsi3 -sin(fi3)*sqr(om3));

di- ada2v(dx,dy,vdx,vdy,adx,ady,cx,cy,0,0,0,0 ,0,0,0,14,0,fi4,om4, epsi4,l5,v5,a5);

CoordXY( 100,200);

xl := ox + round(kl*bx); yl := oy -round(kl*by);

OutTextXY(100,10,'Cxемa механизма');

OutTextXY(30,440, 'Esc - конец работы программы');

str(fil *180/pi:6:2,st1);

str(fi3*180/pi:6:2,st2);str(fi4*180/pi:6: 2,st3);

str(15:6:4,st4);

OutTextXY(30,395, 'Fi1='+ stl + 'град.'+ ' Fi3= ' + st2+ ' град. ');

OutTextXY(310,395, 'Fi4= ' + st3 +' град.' + ' L5=1 + st4 +' м.'); circle(ox,oy,3);

Opora(ox,oy);

OutTextXY(ox + 10,oy + 10,'A');

MoveTo(ox,oy);

LineTo(xl,yl);

OutTextXY(xl + 10,yl –10, 'B'); cir-cle(xl,yl,3);

MoveTo(ox,oy - round(kl*cy)); circle(ox,oy - round(kl*cy),3);

OutTextXY(ox - 10,oy - round(kl*cy) – 10, 'C');

Opora(ox,oy - round(kl*cy));

xl := ox + round(kl*130*cos(fi3));

yl := oy - round(kl*cy) -round(kl*130*sin(fi3));

lineto(xl,yl);

xl := ox + round(kl*lcb*cos(fi3));

yl := oy - round(kl*cy) -round(kl*lcb*sin(fi3));

Postpara(ox + round(kl*bx),oy -round(kl*by),fi3);

xl := ox + round(kl*dx); yl := oy -round(kl*dy);

OutTextXY(xl - 10,yl - 10,'D'); cir-cle(xl,yl,3);

moveto(xl,yl);

x2 := xl + round(kl*14*cos(fi4));

y2 := yl - round(kl*14*sin(fi4)); lineto(x2,y2);

line(ox + 50, y2, ox + 250, y2); Post-para(x2,y2,0);

circle(x2,y2,3);

OutTextXY(x2,y2 – 15, 'E');

{План скоростей}

SetColor(red); OutTextXY(400,10, 'План скоростей');

str(om3:6:2,st2);

str(om4:6:2,st3); str(v5:6:4,st4);

OutTextXY(30,410, 'Oml= 1.00' +' Om3'+ st2);

OutTextXY(310,410,'Om4=' + st3 +'V5=' + st4);

OutTextXY(pvx+5,pvy + 5,'Pv');

xl := pvx + round(kv*vbx); yl := pvy - round(kv*vby);

line(pvx, pvy, xl, yl); {Скорость Vb1,2} OutTextXY(xl + 5,yl + 5, 'b');

x2 := xl - round(kv*v3*cos(fi3));

y2 := yl + round(kv*v3*sin(fi3)); line(х1,у1,x2,у2); {Скорость Vb32} Iine(pvx,pvy,x2,y2);

OutTextXY(x2 - 10,y2 + 5,'b3'); xl := pvx + round(kv*v5); yl := pvy; line(pvx,pvy,xl,yl);

OutTextXY(xl,у1 +5,'e');

x2 := pvx + round(kv*vdx);

y2 := pvy - round(kv*vdy); line(pvx, pvy, x2, y2);

OutTextXY(x2,y2 - 10,'d');

line(xl,yl,x2,y2);

xl := pvx - round(kv*lcb*sin(fi3)*om3); yl := pvy - round(kv*lcb*cos(fi3)*om3); line(pvx,pvy,xl,yl);

{План ускорений} SetColor(blue);

OutTextXY(400,360, 'План ускорений');

str(epsi3:6:2,st2);str(epsi4:6:2,st3);

str(a5:6:4,st4);

OutTextXY(30,425,'Epsi1=0.00 ' +'

Epsi3='+st2);

OutTextXY(294,425,'Epsi4=' + st3 + '

A5='st4);

OutTextXY(pax + 5,pay + 5,'Pa');

xl := pax + round(ka*abx);

yl := pay - round(ka*aby);

line(pax,pay,xl,yl);

OutTextXY(xl - 10,yl + 5,'b');

x2 := xl + round(ka*2*v3*om3*sin(fi3));

y2 := yl + round(ka*2*v3*om3*cos(fi3));

line(xl,yl,x2,y2);

OutTextXY(x2 - 10,y2 + 5,'k');

xl := x2 - round(ka*a3*cos(fi3));

yl := y2 + round(ka*a3*sin(fi3));

line(x2,y2,xl,yl);

OutTextXY(xl -10,yl, 'r');

xl :=pax;yl:=pay;

x2 := xl - round(ka*lcb*sqr(om3)*cos(fi3));

y2 := yl + round(ka*lcb*sqr(om3)*sin(fi3));

line(xl,yl,x2,y2);

OutTextXY(x2 + 10,y2 + 5,'n');

xl := x2 - round(ka*lcb*epsi3*sin(fi3));

yl := y2 - round(ka*lcb*epsi3*cos(fi3)); line(x2,y2,xl,yl);

OutTextXY(xl + 10,yl + 5,'t');

line(pax,pay,xl,yl);

OutTextXY(xl + 10,yl - 10, 'b3');

xl := pax + round(ka*adx); yl := pay -round(ka*ady);

OutTextXY(xl - 10,yl - 10,'d');

x2 := xl - round(ka*14*cos(fi4)*sqr(om4));

y2 :=yl + round(ka*14*sin(fi4)*sqr(om4)); line(xl,yl,x2,y2);

xl := x2 - round(ka*14*sin(fi4)*epsi4);

yl := y2 - round(ka*14*cos(fi4)*epsi4); line(x2,y2,xl,yl);

x2 := pax + round(ka*a5); y2 := pay;

line(pax,pay,x2,y2);

OutTextXY(x2,y2 + 5,'e');

rectangle(20,380,620,455);

rectangle(18,378,622,457);

ch := readkey; if ch = #27 then exit;

if i <>nc then cleardevice;

end;

ch := readkey;

if ch = #27 then exit else goto start;

End.

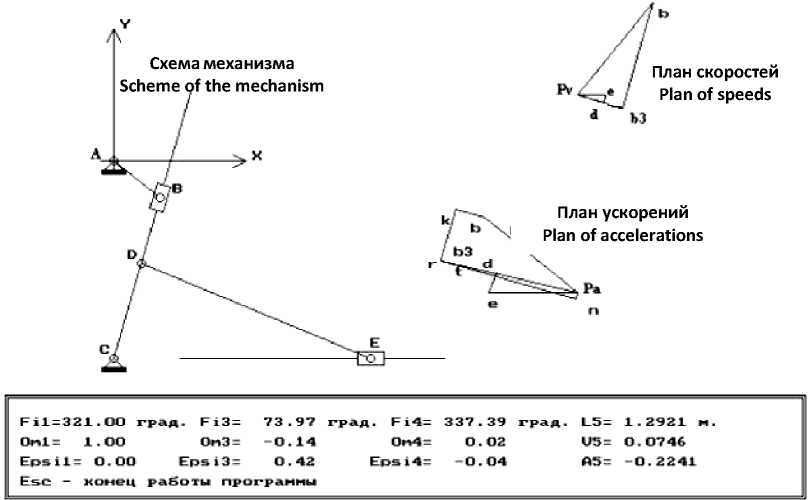
Рисунок 2. Пример работы программы.

• Figure 2.    Example of work of the program.

Использование библиотечных процедур модуля DIADA, позволяет сравнительно просто организовать имитацию движения механизма, рассчитать проекции аналогов скоростей и ускорений всех звеньев механизма, построить планы скоростей и ускорений в каждом положении механизма. Если необходимы значения кинематических характеристик, их можно вывести на дисплей. Такой подход обеспечивает эффективность при определении оптимальной кинематической схемы механизма на основе технического задания.