Программная реализация нечеткого поиска текстовой информации в словаре с помощью расстояния Левенштейна

Нечеткий поиск (поиск по сходству, fuzzy string search) – это поиск информации, при котором выполняется сопоставление информации заданному образцу поиска или близкому к этому образцу значению. Алгоритмы нечеткого поиска используются, например, для: распознавания рукописных символов (как в режиме офлайн – распознавание символов, написанных на бумаге с помощью систем оптического распознавания, так и в онлайн-режиме – считывание движений кончика стилуса, например, по поверхности сенсорного экрана гаджета); проверки орфографии в информационно-поисковых системах (Google, Yandex и др.) а также в системах проверки правописания; решения ряда вычислительных задач в области биоинформатики (например, для сравнения генов, белков и хромосом).

Рассмотрим пример использования алгоритма нечеткого поиска текстовой информации для осуществления проверки введенного пользователем запроса, например, в информационно-поисковую систему. Пусть пользователь вводит слово «града» в поле для ввода запроса. Необходимо найти в БД информационно-поисковой системы все совпадения с заданным запросом (словом «града») с учетом возможных допустимых различий (отклонений) (это может быть, например, «ограда», «рада», «ада»). Чтобы оценить сходство двух слов используют метрики нечеткого поиска. Метрикой нечеткого поиска называют функцию расстояния (d) между двумя строками, позволяющую оценить степень их сходства в данном контексте. В числе наиболее известных метрик – расстояние Хемминга, расстояние Левенштейна, расстояние Дамерау-Левенштейна.

Расстояние Хемминга – это число позиций, в которых соответствующие символы двух строк одинаковой длины различны [1]. Например, для векторов (1011101) и (1001001) расстояние d(1011101, 1001001) = 2, так как эти вектора имеют различие в двух позициях (3 и 5). Расстоянием Хэмминга для кода называют минимальное расстояние между кодовыми строками. Главный недостаток расстояния Хемминга – возможность сравнения строк только одинаковой длины.

Расстояние Левенштейна (редакционное расстояние, дистанция редактирования) в теории информации и компьютерной лингвистике – это мера разницы двух последовательностей символов (строк) относительно минимального количества операций вставки, удаления и замены, необходимых для перевода одной строки в другую.

Рассмотрим рекурсивную функцию. Пусть S 1 и S 2 - две строки

(длиной n и m соответственно) над некоторым алфавитом. Тогда редакционное расстояние d(S1, S2)  можно подсчитать по следующей рекуррентной формуле:

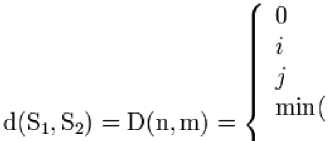
; i = 0, j = О ; j = 0, t > О ; г = 0, j > О

D(i,j-1) + 1

D(i- Lj) + 1 ; j > 0, г > О D(i- Lj - l) + m(Si[i],S₂y])

, где m(a,b) = 0 , если a = b и единице в противном случае; min(a, b, c) возвращает наименьший из аргументов. Здесь шаг по i символизирует удаление (D) из первой строки, по j – вставку (I) в первую строку, а шаг по обоим индексам символизирует замену символа (R) или отсутствие изменений (M). Очевидно, справедливы следующие утверждения: d(S1,S2) ≥ | |S1| – |S2| |; d(S1,S2) ≤ max( |S1| , |S2| ); d(S1,S2) = 0 ↔ S1 = S2.

Пример нахождения расстояния Левенштейна представлен на рисунке 1. В примере рассматривается преобразование строки «EABF» в строку «ABCD». Найденное расстояние Левенштейна d равно трем.

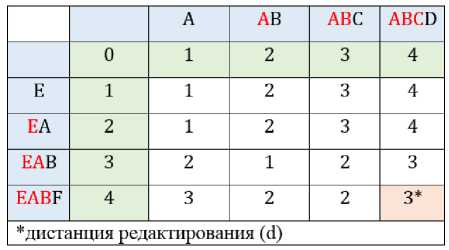
Рис. 1. Пример преобразования строки «EABF» в строку «ABCD»

Результатом работы является программная реализация нечеткого поиска текстовой информации в словаре с помощью расстояния Левенштейна на языке программирования PHP. Программный код представлен ниже. Массив, по которому будет осуществляться поиск информации, содержит имена в транслитерации, а именно: «Daniil», «Zahar», «Dmitry», «Leonid», «Ilia», «Yegor», «Innokenty», «Gennady», «Maksim», «Valentin», «Yevgenia», «Matvey». Существуют имена, которые имеют несколько вариантов написания на английском языке, так как некоторые звуки можно передавать разными комбинациями букв. Например, имя «Евгения» может писаться как «Yevgenia», «Yevgeniya» или «Evgenia». Для гибкого поиска значений массива, редакционное расстояние (d) можно изменять. Таким образом, с помощью нижеприведённого алгоритма можно осуществлять поиск текстовой информации для одинаково звучащих, но имеющих различное написание строк.

Программная реализация нечеткого поиска текстовой информации

Введите слово

Буквенные символы (A-Z;a-z) =

Введите расстояние Левенштейна

Числовое значение (d) <=

$word_entered = ($_GET['a']);

$words_array = array('Daniil', 'Zahar', 'Dmitry', 'Leonid', 'Ilia', 'Yegor', 'Innokenty', 'Gennady', 'Maksim', 'Valentin', 'Yevgenia', 'Matvey');

$shortest_distance = -1;

$word_array_1 = Array();

foreach ($words_array as $word) {

$flagg = 0;

$distance = levenshtein($word_entered, $word);

//echo "distance:$distance; ";

//echo "shortest_distance:$shortest_distance; ";

if ($distance == 0) {

$word_array = $word;

$shortest_distance = 0;

break;

} if ($shortest_distance < 0 and $flagg == 0) {

$word_array_1[]= $word;

$shortest_distance = $distance;

$flagg = 1;

} if ($distance == $shortest_distance and $flagg == 0) {

$word_array_1[]= $word;

$flagg = 1;

} if ($distance < $shortest_distance and $flagg == 0) {

$word_array_1 = array();

$word_array_1[] = $word;

$shortest_distance = $distance;

$flagg = 1;

}

// echo "shortest_distance:$shortest_distance;
";

} echo "
";

if ($shortest_distance == 0) { echo "Введенное Вами слово найдено в исходном массиве данных: $word_array
";

echo "Возможно Вы имели ввиду следующее(-ие) слово(-а): ";

echo implode(', ', $word_array_1);

} if ($shortest_distance >= (($_GET['b'])+1)){ echo "Введенное Вами слово не найдено в исходном массиве данных.
";

}

} else { echo "Ошибка! Проверьте корректность введенных данных.";

echo "
";

}

}

?>

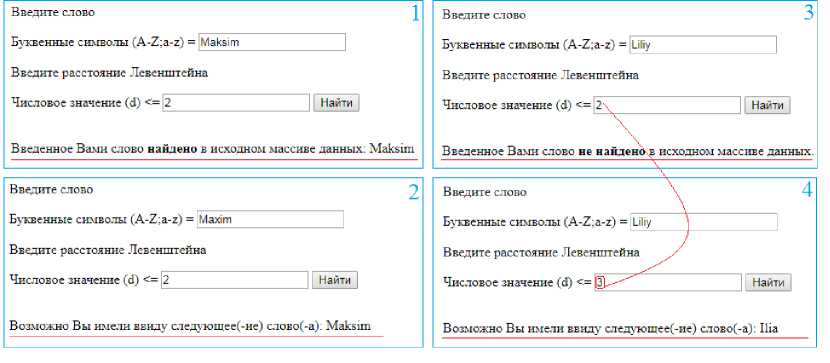
Примеры результатов поиска текстовой информации с учетом редакционного расстояния представлены на рисунке 2. Результатом запроса может быть одно из следующих сообщений: введенное Вами слово найдено в исходном массиве данных; возможно Вы имели ввиду следующее(-ие) слово(-а) <...>; введенное Вами слово не найдено в исходном массиве данных; ошибка! Проверьте корректность введенных данных.

Введите слово

Буквенные символы (A-Z:a-z) = |Maksim

Введите расстояние Левенштейна

Числовое значение (d) <= |2                      1 1 Найти |

Введенное Вами слово найдено в исходном массиве данных:

Введите слово

Буквенные символы (A-Z;a-z) = |Liliy

Введите расстояние Левенштейна

Числовое значение (d) <= |2\

Введенное Вами слово не найдеш

Введите слово

Буквенные символы (A-Z:a-z) = Maxim ~

Введите расстояние Левенштейна

Числовое значение (d) <= |2                      ] | Найти |

Возможно Вы имели ввиду следующее(-ие) слово(-а): Maksim

Возможно Вы имели ввиду следующее(-ие) слово(-а): Ilia

Maksim

| Найти |

Введите слово

Буквенные символы (A-Z:a-z) = Lilly

Введите расстояние Левенштейна

Числовое значение (d) <= |3]--"'

| Найти |

Рис. 2. Примеры результатов поиска текстовой информации в исходном массиве данных

Следует отметить, что определение расстояния между словами или текстовыми полями по Левенштейну обладает следующими недостатками: при перестановке местами слов или частей слов получаются сравнительно большие расстояния; расстояния между совершенно разными короткими словами оказываются небольшими, в то время как расстояния между очень похожими длинными словами оказываются значительными. Таким образом, для более гибкого поиска различий между двумя последовательностями символов рекомендуется использовать другие методы и алгоритмы, например, BK-деревья, метод N-грамм, алгоритм расширения выборки.