Программная система анализа производительности компьютерных сетей на основе аппроксимационного подхода

Для решения задачи анализа производи-тельностисети,заключающейсявопределении всех основных узловых и сетевых характеристик, ее модель должна быть декомпозирована на отдельные узлы с вычислением характеристик входных и выходных потоков в каждом узле. После этого уже могут быть вычислены узловые и сетевые характеристики.

Знание и прогнозирование характеристик потоков важно также для оптимального или близкого к нему управления ими в сетях. В настоящее время теория массового обслуживания не позволяет точно определить характеристики потоков в сетевых моделях при произвольных законах распределения времени поступления и обслуживания. Для этого можно использовать только аппроксимационный подход.

Постановка задачи

Рассмотрим открытую сетевую модель с матрицей вероятностей передач P = { p_{i j} }, ( i , j = 1; 2 … n ), где p_{i j} – вероятность того, что заявка, покидающая узел S_i поступит в узел S_j . Для начала – пусть узел представляет собой одноканальную (многоканальную с равновозможным доступом) систему G / G /1 c бесконечной очередью. Для этой системы определены числовые характеристики случайного времени обслуживания: Тц , – среднее значение и – дисперсия времени обслуживания. Для внешнего потока задана совокупность средних значений Tq и дисперсий D_o времени между соседними заявками потока, входящего в узел S_i .В последующем узел может быть представлен как СМО с конечной очередью с потерями.

Для декомпозиции такой модели на отдельные узлы на уровне средних значений и дисперсий времени поступления и обслуживания заявок не существует точных методов. Во многих случаях, например, в [1-2], пользуются только уравнениями равновесия потоков на уровне их интенсивностей Х;- . Такой подход при произвольных потоках в сети МО означает описание случайного потока событий только его средним значением, то есть математическим ожиданием без учета моментов высших порядков. Поэтому учет дисперсий (вторых моментов распределений) интервалов времени существенно может улучшить результаты расчетов.

Поясним это на простом примере эволюции систем массового обслуживания (СМО). Как известноиз[1],среднеевремяожиданиявСМО

M / M /1 выражается равенством ^ =      ;

1- Р

- X М(Х^И для системы M / G /1 –                     .

1-р

Здесь М ( Х ²) означает 2-й начальный момент времени обслуживания. Наконец, для системы G / G /1 это время равно

^=£лч±£>:£_Н

2ч(1-р) 27

Последнее выражение включает дисперсии времен поступления и обслуживания, а также второй начальный момент времени простоя СМО, который неизвестен. Способ его определения показан в [2]. Из приведенных выражений следует, что при анализе сетей СМО G / G /1 необходимо учитывать вторые моменты распределений времени поступления и обслуживания. Как это можно реализовать на практике, видно будет из последующих разделов статьи.

С другой стороны, описание потоков на уровне двух первых моментов распределений интервалов времени означает либо их аппроксимацию непрерывным диффузионным процессом с соответствующими характеристиками [1 -2], либо аппроксимацию их законов распределений известными функциями на уровне двух моментов.

Для этого рассмотрим подробнее структуру потоков отдельного узла с номером i сетевой модели (рис. 1), где А – точка мультиплексирования потоков, В – точка демультиплексирования потока. Из структуры узла (см. рис.1) следует, что на вход i -го узла в общем случае поступает агрегированный поток из разреженных потоков с выходов других узлов.

Следовательно, нам необходимо знать математические операции агрегирования (мультиплексирования) двух потоков и их разрежения на уровне двух моментов. При этом в качестве математической модели потока рассматриваем случайный поток событий на оси времени. Кроме этого необходимо знать и метод определения числовых характеристик выходного потока из СМО. Определение характеристик выходного потока и характеристик СМО G / G /1: среднего времени ожидания, средней задержки и т.п. изложено в [2].

Решением системы уравнений (1) равновесия потоков относительно интенсивностей λ_i потоков на входе и выходе каждой СМО сети определяем средние значения интервалов времени между соседними заявками т = X"j для каждого потока в сети:

К = Ki + ^Pji^Xj 0 = 1 - ^И),      (1)

7=1

где Xqz- – интенсивность потока извне в i-ый узел (см. рис. 1). Дальнейшая задача состоит в получении аналогичных уравнений равновесия относительно дисперсий времени в потоках. Для этого автором в статье [3] использован следующий математический аппарат.

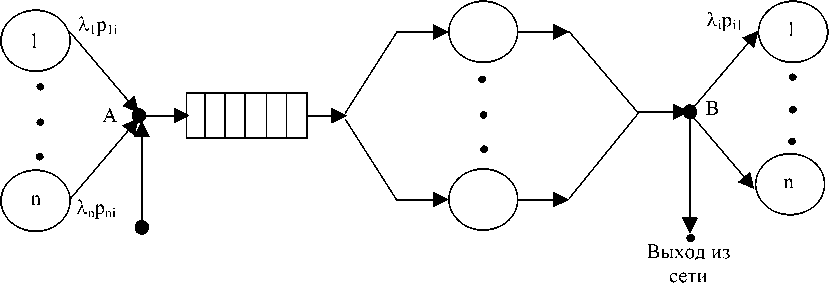
Рис. 1. Структура потоков в z'-ом узле

Математические операции агрегирования двух потоков

Функция распределения интервала времени Tv результирующего потока при мультиплексировании двух потоков с интенсивностями ^ и Ал определяется интегральным соотношением:

^F4 W = 1 - т^Г {[1 - F (/)]j[l - F^ 1и№ +

Л| + ^2                      2

-                       (2)

+ [1-^2O)]J[1-fIi w, где (j =1; 2), а FT j О) – функция распределения интервалов времени между событиями в потоке j (j = 1; 2). Из последнего выражения следует, что среднее значение интервала в результирующем потоке iv = 1/(X1 + X2) = 1/AS,(3)

а дисперсия

\ co1

^(Tz) = 2“H" ki 0) • 81 (t)dt - — , оA£ где функции g\(?) = 1 [1 - Fi («)] du , g2 (?) = Я1 - F2 (zz)] du •

Несложно проверить,что применение этих формул к двум пуассоновским потокам дает снова пуассоновский поток.

Из результата (4) вытекают два важных следствия.

• 1.    Под интегралом в выражении (4) стоит произведение двух функций, и, таким образом, в общем случае дисперсию величины Tv – интервала времени между событиями результирующего потока – нельзя будет выразить в виде элементарной функции от дисперсий и математических ожиданий составляющих (кроме случая пуассоновских потоков). Таким образом, дисперсия и моменты высших порядков распределения величины T^ неразложимы.

• 2.    Этот интеграл можно вычислить только при конкретных выражениях функций распределений F_j ( t ). Тогда в условиях неполной информации о потоках в сетевой модели, то есть

когда мы не знаем их законов распределения, остается единственно возможный путь для его вычисления через элементарные функции – это аппроксимация функций g;W 0= 1;2)на уровне двух первых моментов распределений интервалов времени.

Таким образом, будем считать, что потоки в сетевых моделях определены на уровне средних значений Ту и дисперсий D_T распределений интервалов, и функции распределения F _j( t ) будем аппроксимировать отдельно при Cxj и c_Xj>x 0 = i; 2), то есть в зависимости от хвостов распределений. В случае, когда оба агрегируемых потока имеют коэффициенты вариаций c_Xj

РДП =

0, z < т „ l-exp{-(Z-T/1)/Ty2}, Z>Tyl

В том случае, когда обе составляющих потока имеют коэффициент вариации C^ j ^ ^ , выбираем гиперэкспоненциальное распределение:

Fj (0 = 1- PjeM-^PjtlT^ - (6)

.

В смешанном случае очевидно, что имеет место комбинация этих функций. Неизвестные параметры распределений (5) и (6) определяются через числовые характеристики исходных потоков известным методом моментов. Тогда подставим функции g j (0 ( j = 1; 2) с однозначно определенными их параметрами в выражение (4) и после вычисления всех интегралов (табличных) можем определить дисперсию интервала времени мультиплексированного потока.

Имитационное моделирование статистического мультиплексирования по выражению (4) с использованием широкого класса распределений показало, что в случае C^ 7 > ^ ( j = 1; 2) для вычисления дисперсии оказалась точнее формула, основанная на диффузионном приближении потоков [3]:

D^ -C^)³ D_Ti+(X₂/X_z)³ D₄. (7)

Таким образом, в алгоритме программы мультиплексирования двух потоков заложены (4)-(5) в зависимости от величины коэффициентов вариаций агрегируемых потоков.

Вероятностное разрежение потока

Как было отмечено выше, для вывода уравнений равновесия относительно дисперсий необходимо знать характеристики (среднее значение и дисперсию) разреженного потока. Для этого кратко воспроизведем доказанный результат, полученный автором в статье [3].

Пусть мы имеем точку демультиплексирования потока (т. В на рис. 1), в которой заявки с вероятностью p уходят из потока (просеянный поток 2 на рис. 2). Назовем эту операцию вероятностного разрежения потока p -преобразованием. Тогда среднее значение и дисперсия времени между соседними событиями в просеянном потоке

^_P =^l P, (8)

^DT_P = ^dVp + f² C¹ - pW~ ■ (9)

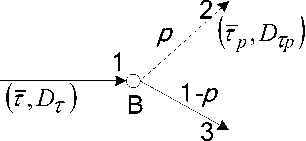
Рис. 2. Демультиплексирование потока ( p -преобразование)

Определение первых двух моментов распределения выходного потока из СМО

Вернемся к структуре узла сетевой модели, показанной на рис. 1, из которой видно, что на вход i -го узла в общем случае поступает агрегированный поток из разреженных потоков с выходов других узлов. Для этого необходимо знать дисперсии распределения интервалов между событиями в выходных потоках. Воспользуемся результатами автора, полученными в статье [2], которые представим в виде следующего утверждения.

Пусть          i^niD – соответственно, средние значения и дисперсии времен между заявками в выходном потоке из CMO GI/G/1/∞ и обслуживания. Тогда справедливы следующие аналитические выражения для определения вых? вых вых ^ ц ~*~ Р^^Х,            (10)

D_eblx=D^p^l₀D^l_xxM\-pWx )², (11)

где р Q – вероятность того, что обслуженная заявка оставляет СМО пустой, т^ и ^х – среднее значение и дисперсия остаточного времени т^, в течение которого СМО ожидает поступления непосредственно следующей заявки,то есть времени простоя СМО.

Все вышеприведенные основные результаты (3)-(4), (7)-(11) по операциям с потоками проверены на адекватность имитационным моделированием – методом Монте-Карло – на широком классе распределений от равномерного до распределения Вейбулла. При этом относительная погрешность результатов не превышает 5% [2-3].

Для имитационного моделирования была разработана специальная программа «Агрегирование и разрежение потоков событий методом Монте-Карло» [4]. Теперь по аналогии с уравнениями равновесия потоков на уровне их средних значений (1) можем записать уравнения равновесия относительно их дисперсий.

Используя формулы (4), (7) и (9) для суммы разреженных потоков на входе i -ой СМО сетевой модели, дисперсию интервалов времени между соседними заявками в суммарном входном потоке в стационарном режиме можно выразить через известные параметры сети и дисперсии ^вых j выходных потоков j -ой СМО сети ( i , j = 1; 2 … n ) (см. рис.1):

^DiBX -«П., ^Цвых^Жчвых^вьвЖ¹²)

c_nj⁼^<^D!.»⁺P%^; (‘J= i; 2 - * (i3) ^pj‘ ' Pji‘^xj

Алгоритм работы программной системы, использующий описанный выше математический аппарат потоков событий,включает следующие этапы.

• 1.    На первом этапе сеть массового обслуживания считаем экспоненциальной и решением системы уравнений (1) определяем интенсивности потоков на входе и выходе каждого узла. Следовательно, будут определены математические ожидания и дисперсии интервалов времени в потоках на входе и выходе каждого узла.

• 2.    На втором этапе используем метод двумерной диффузионной аппроксимации процессов функционирования систем массового обслуживания G /G /1 и уточняем дисперсии входных и выходных потоков по формулам (12) совместно с (11) и (13). Как показывают практические расчеты, такая итерационная процедура включает всего несколько итераций.

• 3. На заключительном этапе в программе определяются все основные узловые и сетевые характеристики: загрузки, средние времена задержек,средние длины очередей и др.

Основные процедуры программной системы

На рис. 3 приведена экранная форма программной системы. В функции меню «Расчет узла» предусмотрен расчет основных характеристик СМО G / G /1 – подменю «Узел с бесконечной очередью» и СМО G / G /1/ k – подменю «Узел с конечным буфером и потерями». Расчеты реализуются процедурами VNG G1 и VNGGM соответственно.

7'Вероятностное моделирование

Расчет узла Рачет сети О программе Выход

Программная система анализа производительности компьютерных сетей на основе аппроксимативного подхода

ВС с однородным трафиком ВС с многомерным трафиком

Рис.3. Экранная форма программы

Вменю«Расчетсети»реализованрасчетосновных характеристик сетевой модели как с однородным,так и с неоднородным трафиком.В первом случае расчет проводится без учета типов трафика и протоколов,а во втором – с учетом их.Расчеты реализуются соответственно процедурами Uodnet и Uneodnet.Данные процедуры реализуют все расчеты по приведенному выше алгоритму.Для расчета дисперсий времени попарно мультиплексируемых потоков по формулам (4) и (7)реализована процедура Multipl.

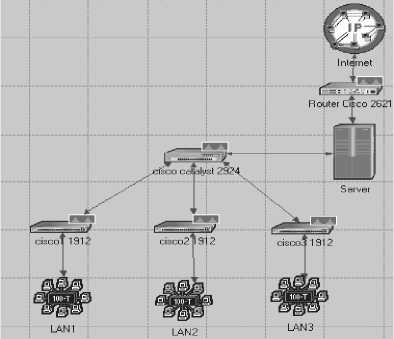
Рис.4. Структура сети кафедры вуза

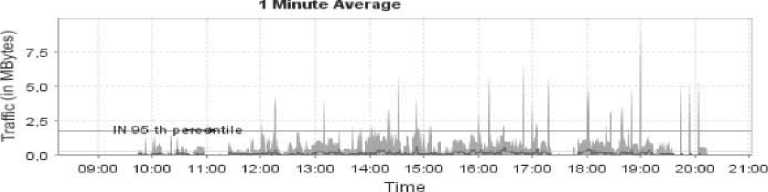
В заключение рассмотрим применение прграм-мной системы к расчетам реальных сетевых структур. На рис.4 приведена структура сети кафедры, вы- полненнаявсистеме моделированияOPNET Modeler. Сетевая модель включает в себя 8 узлов,среди них сервер,главный коммутатор,коммутаторы подсетей LAN1-LAN3,подсети LAN1-LAN3 и 8 каналов связи 100Мбит/с.ПодсетиLAN1-LAN3включаютпо10ра-бочих станций,поэтому следует ожидать,что потоки будут симметричными.Учитываятот факт,чтообмен данными между сервером и главным коммутатором, а также между главным коммутатором и остальными коммутаторами в обе стороны по каналам связи примерно одинаковые,матрицу вероятностей передач определим так,как показано на рис.6.Остальные исходные данные определим из анализа дневного трафика сети,представленного на рис. 5.Его подробный анализ показал,что коэффициент вариации интервала между пакетами равен 2.Максимальное значение трафика (срез случайного процесса)в пересчете на пакеты порядка 584.

Результаты расчетов по авторской программе приведены на рис.7.Из них видно,что в главных узлах 1 и 2 интенсивность потоков составляет около 1168 пак/С.Этовполнеожидаемыйрезультат,таккак мы имеем здесь 3 идентичных сегмента, в каждом из которых циркулирует 389 пак/С. Загрузка главных узлов,как и ожидалось,равна примерно 15%.

Эта же сеть для проверки на адекватность расчетов была промоделирована в программной системе имитационного моделирования OPNET Modeler. Структура сети приведена на рис.4,а разультаты моделирования – на рис.8.Сравнение результатов по загрузкам каналов сети по обеим программам показывает их полное совпадение.Преимущество авторской программы при анализе производительности сетей заключается в том,что по сравнению с имитационным моделированием здесь расчеты выполняются за доли секунды.

Traffic Report

IP Group Name :

Graph : volumel

Report Start Time

Report End Time.

2009 04-28 08-15

2009-04-28 21.02

Category	Total	Max	Min	Avg	95th Percentile
□ Traffic IN	434.83 MB	9.47 MB	0.00	566.18 KB	1.72 MB
□ Traffic OUT	59.14 MB	608.43 KB	0.00	77.01 KB	262.54 KB

Рис.5. Входящий и исходящий трафики сети кафедры

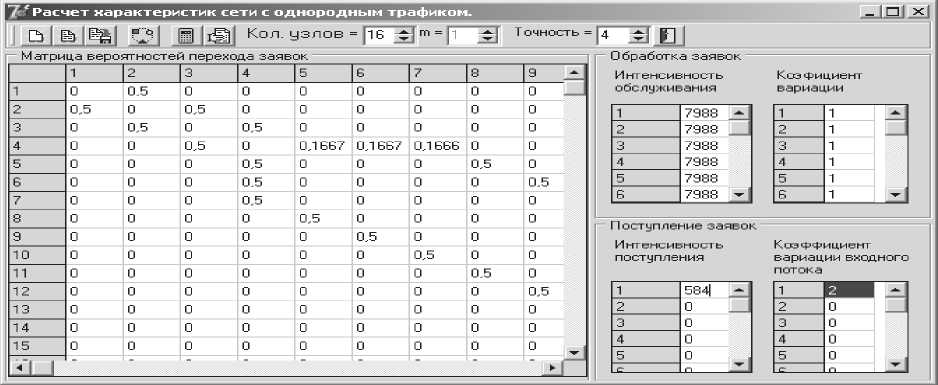
Рис. 6. Исходные данные к расчету сети

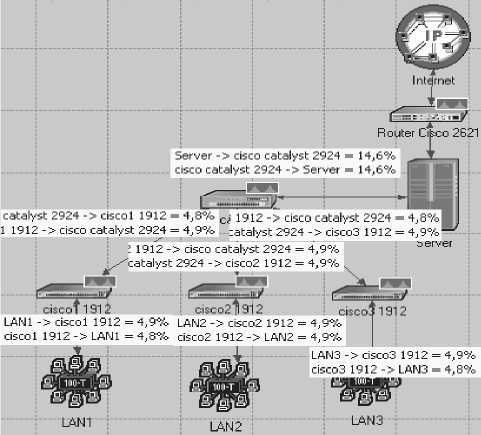
Рис.8. Результаты расчетов по программе OPNET Modeler

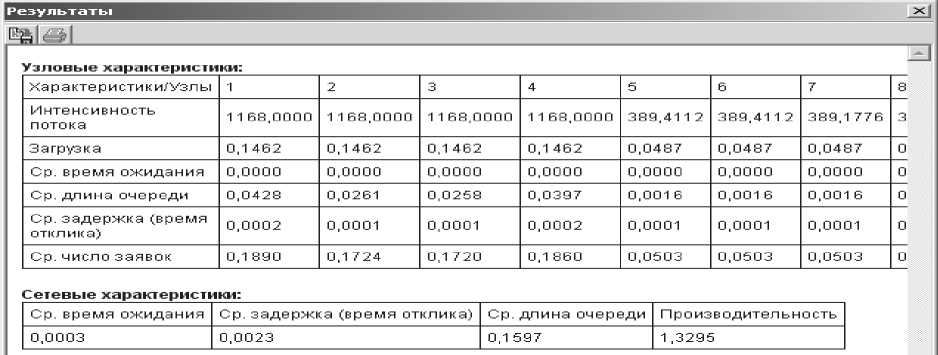
Рис.7. Результаты расчетов по программной системе