Программно-методический подход к моделированию динамики посадки лунного взлётно-посадочного корабля

Миссия к Луне является перспективным проектом, включенным в Федеральную космическую программу России на 2015–2025 гг. [1]. В рамках этого проекта должен быть решен целый ряд задач, в т. ч. задача обеспечения мягкой посадки лунного взлетно-посадочного модуля [2]. Моделирование динамики процесса посадки на Луну сопряжено с рядом трудностей, вызванных частичным или полным незнанием целого ряда факторов, непосредственно влияющих на процесс посадки, в частности, рельефа и физико-механических свойств посадочной поверхности в месте первого контакта [3]. Кроме того, всегда имеет место разброс массово-инерционных характеристик самого корабля и кинематических начальных условий (скорость и ориентация корабля относительно посадочной поверхности). В то же время, необходимо выполнить ряд требований, предъявляемых к процессу посадки: ограничение нагрузок на экипаж и конструкцию, устойчивость (отсутствие переворота) и обеспечение минимально допустимого клиренса между корпусом аппарата и посадочной поверхностью [4–12]. В связи с этим возникает необходимость разработки рекомендаций для определения параметров посадочного устройства, таких как кинематическая схема и энергетические характеристики демпфирующих элементов, с учетом проектных ограничений.

Для разработки такого рода рекомендаций применительно к процессу посадки лунного взлетно-посадочного корабля (ЛВПК) необходима разработка математической модели процесса посадки и ее реализация, поэтому требуется решить следующие задачи:

• 1.    Разработка математической модели, включающей:

• •    дифференциально-алгебраические уравнения:

  – уравнения движения;

  – уравнения связей;

• •    определение силовых факторов, действующих в процессе посадки:

  – сила амортизатора в посадочной опоре;

  – сила взаимодействия с грунтом.

• 2.    Выбор оптимальных параметров — силовой характеристики амортизатора.

• 3.    Статистический анализ по данным процесса посадки — определение критичных и оптимальных сочетаний начальных условий.

модель и механическая система

На рис. 1 представлен общий вид ЛВПК.

Корабль рассматривается как структурно сложная механическая система тел с внутренними связями, характер которых отражает ограничения на движение взаимодействующих тел, обусловленные конкретной конструкцией опор посадочного устройства. На рис. 2 схематично изображена система тел и взаимосвязи между ними.

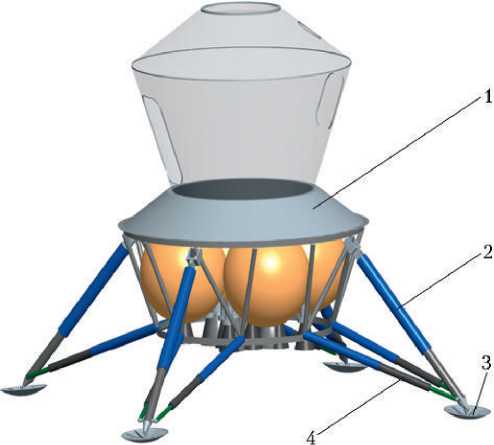
Рис. 1. Общий вид лунного взлетно-посадочного корабля (ЛВПК): 1 — ЛВПК; 2 — основная опора; 3 — тарель; 4 — подкос

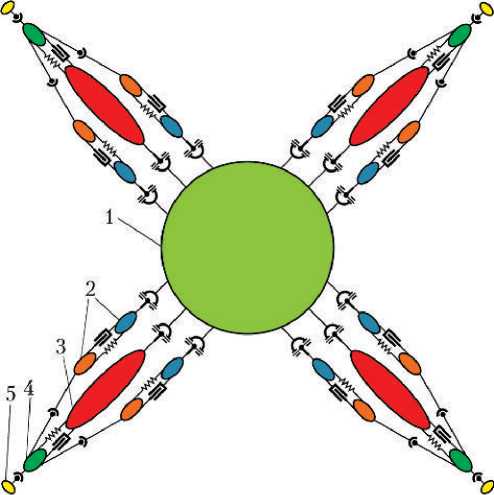
Рис. 2. Схема механической системы: 1 — лунный взлетнопосадочный корабль; 2 — подкос; 3 — основная опора (цилиндр); 4 — шток основной опоры; 5 — тарель; — сила (амортизатор); — шарнир Гука (кардан); — сферический шарнир; — цилиндрический шарнир

уравнения движения и уравнения связей

Математическая модель процесса посадки основана на методах теоретической механики. В ряде публикаций [13–15] авторами проведено детальное рассмотрение математической модели посадки пилотируемого корабля «Федерация» [16], составлены уравнения движения (1), (2) и уравнения связей (4)–(7) для каждого типа механического соединения между отдельными телами системы (корпус аппарата, элементы опоры посадочного устройства — цилиндр, шток, опорная тарель).

Движение ЛВПК с посадочным устройством (ПУ) моделируется механической системой тел, состоящей из центрального тела (корпуса ЛВПК) и тел, составляющих ПУ. Уравнения поступательного перемещения центра масс каждого тела рассматриваемой механической системы и уравнения вращательного движения относительно центра масс, соответственно, будут иметь вид [12–14]:

m _i a _i = F _oi + r _i ; (1)

[Ioi]εi + ωi×([Ioi]ωi) = loi + li + l(ri)ci, (2) где ai и εi — ускорение центра масс и угловое ускорение i-го тела системы, соответственно; mi и [Ioi] — масса и тензор инерции i-го тела, соответственно; ωi — угловая скорость тела; Foi — главный вектор внешних сил; ri — главный вектор сил реакций связей, действующих на i-е тело; loi — главный момент внешних сил; li — главный момент сил реакций связей; l(ri)ci — главный реактивный момент.

Решая уравнения (1) и (2) относительно старших производных, получим следующую систему уравнений:

• r i

• v i

•

ω

i

v

i m- 1(F oi + Ri)             >,

J — 1 ( — “ i ' J ^ i ⁺ L Oi ⁺ L i ⁺ L ( R i )_a)

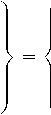
где r ^. _i — производная по времени радиус-вектора перемещения центра масс тела ( v _i — скорость центра масс); v ^. _i — производная скорости центра масс тела (ускорение) и ω ^. _i — производная угловой скорости (угловое ускорение).

Уравнения движения (3) не могут быть сразу проинтегрированы, поскольку кроме внешних сил и моментов в них входят неизвестные силы и моменты реакций связи. Для определения этих неизвестных существует подход, который заключается в дополнении системы дифференциальных уравнений специальными уравнениями связей.

Для каждого типа механической связи записываются векторные уравнения, основанные на условии нерасхождения в шарнирной точке соединения (4) и условии равенства проекций угловых скоростей контактирующих тел на оси, ортогональные оси относительного разворота (5):

r _i + r _ij = r _j + r _ji ; (4)

ω _i – ω _j = 0, (5)

где j — индекс тела, соединенного с i -м телом; r _ij и r _ji — шарнирные векторы (рис. 3).

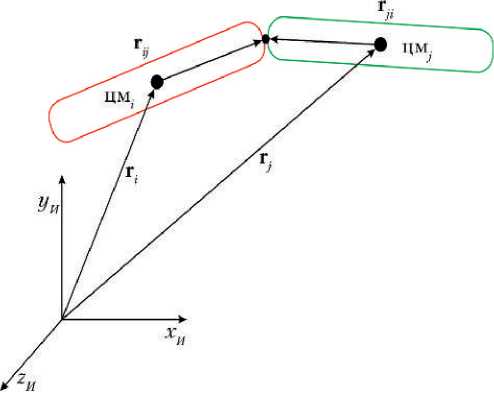
Рис. 3. Кинематическая схема соединения двух тел

После двойного дифференцирования выражения (4) и (5) приобретают, соответственно, вид (6) и (7).

a _i + ε _i × r _ij + ω _i × ( ω _i × r _ij ) + 2 ω _i × v _ij + a _ij =

= a _j + ε _j × r _ji + ω _j × ( ω _i × r _ji ); (6)

ε _i – ε _j + ω _i × ω _j = 0, (7) где v _ij — относительная линейная скорость двух тел в точке связи.

Следует отметить, что выражения (6) и (7) являются универсальными и позволяют отразить любой тип механической связи (количество степеней свободы в связи).

Из уравнений движения (1), (2) и уравнений связи (6), (7) составляется система дифференциально-алгебраических уравнений (ДАУ) вида

M Q.A Г q

Q 0 JL <

= в ,

где M — обобщенная матрица инерции; Q — матрица коэффициентов уравнений связей; q ^.. — вектор-столбец ускорений; λ — вектор-столбец реакций связей.

Решение ДАУ (8) как системы линейных алгебраических уравнений относительно неизвестных позволяет получить реакции связей и ускорения, после чего следует интегрирование системы уравнений (3).

Помимо непосредственно динамических уравнений движения, в систему (3) входят кинематические уравнения для определения коэффициентов матрицы преобразования между локальной и инерциальной системами координат для каждого тела, которые имеют вид:

e _k = – ω _i × e _k , k = 1, 2, 3, (9)

где e _k — орты невращающегося вектора в инерциальной системе координат. Выражение (9) представляет собой девять дополнительных дифференциальных уравнений первого порядка, из которых непосредственно определяются элементы матрицы преобразования.

Таким образом, итоговая система дифференциальных уравнений, готовых для численного интегрирования, будет выглядеть следующим образом:

.

r

i

.

v i₌

.

ω

i

.

e k i = 1, ..., n,

v

i m- 1(F oi + R i)

J^{- 1} ( - w i x J i m i + L oi + L i + L _a .)

- w i x e k

где n — количество тел системы.

Описанный подход универсален для механических систем со структурой дерева и реализован программно. В качестве средства программной реализации был выбран язык программирования Python с использованием библиотек NumPy и SciPy.

Сила амортизатора посадочного устройства

В рассматриваемой задаче энергопоглотитель опоры посадочного устройства представляет собой сотовую конструкцию, которая отличается отсутствием восстанавливающей силы, позволяющей вернуться в исходное положение после остаточной деформации.

Зависимость усилие–деформация (рис. 4) для деформирующихся элементов ПУ со ступенчатой характеристикой может быть представлена в общем виде [6]:

F ( x ) = Σ _i { F _i U ( x _{( i +1)} – x )[1 – U ( x _i – x )] +

+ [Fi–1 + Cs(x – x(i))]U(xi – x)[1 – U(x(i) – x)]}, где U(x) — единичная ступенчатая функция:

U(x) =

0 , x >  0

1, x <  0

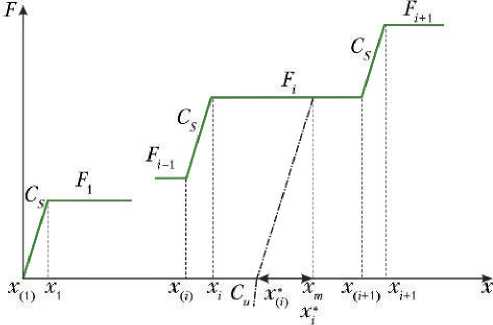
Рис. 4. Ступенчатая характеристика усилие–деформация

При повторном нагружении изменения в зависимости усилие–деформация определяются условиями:

• •    если x <  x _i *, то F * = – C _u ( x _i * – x ). После разгрузки сот, т. е. когда энергопоглотитель исчерпал упругую деформацию при обратном ходе (растяжении), шток опоры встает на более жесткий упор жесткостью C _u (конструктивно может быть выполнен в виде линейной «трещотки»). Таким образом, шток не возвращается в свое изначальное положение, а остается в новом положении динамического равновесия;

• •    если x _{( i )}* <  x <  x _m , то F * = C _s ( x _m – x ) — участок упругой деформации сжатых сот, где C _s — жесткость сжатых сот. Если перемещению соответствует некоторая полка силы F _i ступенчатой функции, то при переходе от сжатия амортизатора к его растяжению сила не принимает нулевого значения, а соответствует характеристике линейной деформации.

Параметры с индексом «*» используются для определения силы в случае повторного нагружения опоры.

Сила грунта

В качестве посадочной поверхности рассматривается плоскость без локальных неровностей. Взаимодействие с грунтом описывается реологической моделью Фойг-та, которая представляет из себя упруговязкую силу σ:

σ = Cyi + ηyi', где C, η — коэффициенты жесткости и вязкости грунта, соответственно; yi и y' — вертикальное перемещение i-ой точки грунтовой поверхности в зоне контакта и вертикальная скорость, соответственно.

критерии выбора оптимальных параметров посадочного устройства

Как отмечалось, процесс посадки должен удовлетворять следующим критериям:

• •    ограничение нагрузок на экипаж и конструкцию (оценивается ускорениями при посадке);

• •    отсутствие переворота в процессе посадки;

• •    отсутствие контакта корпуса с посадочной поверхностью.

Все перечисленные требования можно объединить и обозначить их выполнение как случай успешной посадки, невыполнение хотя бы одного из требований — как неуспешной. Таким образом, имея заданные диапазоны всех начальных условий, можно сформировать список сочетаний начальных условий и провести моделирование по каждому элементу такого списка.

В процессе моделирования для оценки успешности процесса посадки полученные результаты (ускорения центра масс, реакции в точках соединения тел, зазор между корпусом и посадочной поверхностью и угловую ориентацию корпуса в пространстве), согласно требованиям, необходимо фиксировать.

Полученные результаты обрабатываются, и проводится статистический анализ, который показывает, сколько реализовано успешных и неуспешных случаев, какие требования не выполнены для каждого конкретного случая, какова вероятность неуспешной посадки. Аналитика подобного процесса детально рассмотрена авторами в работах [13–15].

используемые технологии и распределение задач

Существуют различные подходы к решению задач моделирования динамических процессов механических систем: использование готовых специализированных программных продуктов, разработка собственного инструмента под конкретную задачу, либо рациональное сочетание этих двух подходов.

Выбор технологий обусловлен их востребованностью в соответствующих областях. Продукты MSC Software покрывают весьма широкий спектр инженерных задач и являются довольно распространенными на профильных производствах. Поэтому масштабные и сложные задачи, в которые помимо моделирования динамики входит анализ нагрузок и прочности, весьма успешно реализуются в продуктах MSC Software .

Python — язык программирования, используемый в веб-разработке, науке, машинном обучении, обработке данных, аналитике и т. д. Он сочетает в себе мощь языков программирования с простотой использования предметно-ориентированных языков типа MATLAB или R , идеален для прототипирования.

Однако у каждой технологии есть свои сильные и слабые стороны (таблица), поэтому, объединив все лучшее от каждой (или дополнив одну другой), можно получить систему, автоматизирующую процесс моделирования и анализа.

На базе принципа декомпозиции сложной и многоэтапной задачи на ряд простых строится методика создания рассматриваемой системы моделирования и анализа. А именно, рассматривается распределение задач между Adams и собственной программной реализацией. Основные функциональные этапы системы моделирования и анализа можно определить как:

• •    формирование модели системы тел с их взаимосвязями в Adams и экспорт данных модели для создания прототипа модели;

• •    составление уравнений движения, уравнений механических связей и формирование системы ДАУ. Разработка универсального алгоритма формирования ДАУ в зависимости от топологии системы и типа соединения между телами;

• •    прототипирование модели — разработка кодовой базы математической модели

на Python для отладки алгоритмов и функций, качественная оценка, формирование расчетных случаев и подход к статистическому исследованию;

• •    моделирование в Adams расчетных случаев и статистики;

• •    анализ данных моделирования, статистический и вероятностный анализ, выводы.

  Сопоставление MSC Adams и Python

  MSC Adams	Python
  + Графический интерфейс + Скорость разработки модели + Визуализация + Аналитика процесса + Высокая производительность вычислений	+ Высокая скорость разработки + Простой синтаксис + Огромное количество прикладных библиотек + Интерактивный режим
  – Ограниченные возможности создания собственных функций – Неудобное управление процессом решения – Отсутствие поддержки современных стандартов языков программирования C и Fortran при написании собственных функций	– Относительно низкая производительность

  
  

  Последовательное выполнение описанных этапов позволяет получить данные исследуемого процесса. В качестве такого процесса рассматривалась посадка на Луну. На рис. 5–7 показаны перегрузка, линейная и угловая скорости ЛВПК, соответственно, с момента первого контакта тарели посадочного устройства с грунтом. Они являются ключевыми характеристиками процесса посадки для одного из штатных случаев.

  На рис. 8 представлена энергетическая характеристика амортизатора, которая получена в результате большого количества оптимизационных расчетов и является наиболее приемлемой с точки зрения выполнения требований к процессу посадки, для определенной конфигурации корабля и соответствующих штатных условий посадки.

  
  
  

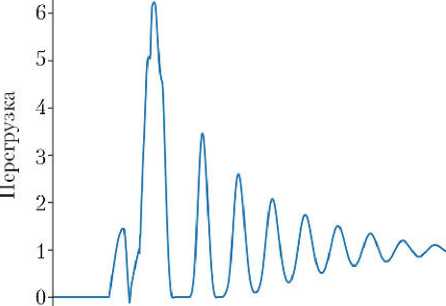
  О 1     2     3     4     5     6 U'

  Рис. 5. Перегрузка в центре масс

  
  
  

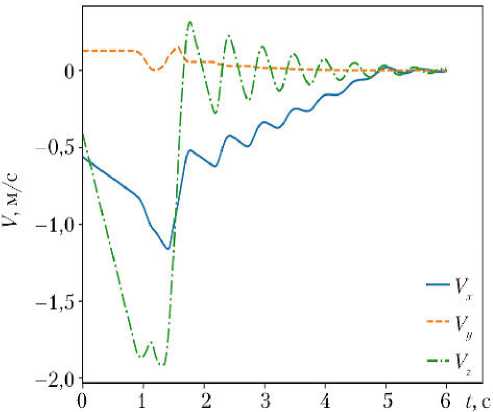
  Рис. 6. Компоненты линейной скорости в центре масс

  
  
  

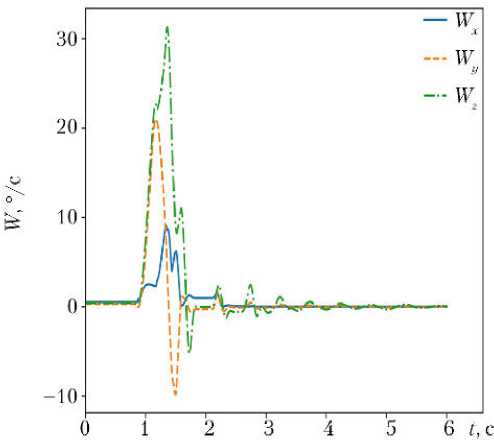
  Рис. 7. Компоненты угловой скорости

  
  

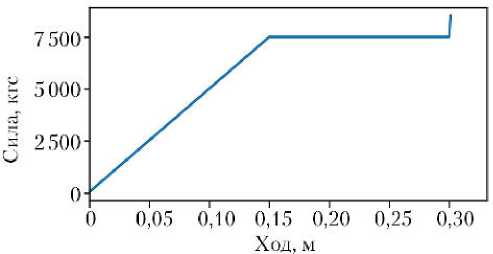
Рис. 8. Энергетическая характеристика амортизатора

В ы вод ы

Для рассматриваемой в данной статье конкретной задачи — моделирования процесса мягкой посадки лунного взлетнопосадочного корабля — применение предложенного подхода позволило в короткие сроки разработать модель процесса, получить ключевые характеристики процесса посадки (см. рис. 5–7) и подобрать энергетическую характеристику амортизатора посадочной опоры, при которой удовлетворяются требования по ограничению перегрузок при посадке, устойчивости движения и минимальному клиренсу. Подход может служить базой для анализа разнообразных процессов, сопровождающихся механической трансформацией объектов ракетнокосмической техники, таких, например, как раскрытие и выдвижение солнечных батарей, разделение ступеней и т. д.

Полномасштабная реализация данного подхода позволит получить следующие результаты:

• •    создание замкнутой системы моделирования и анализа;

• •    существенное сокращение времени разработки и анализа за счет инструментов отладки, автоматизации и тестирования;

• •    возможное сокращение времени в массовых и статистических расчетах процессов механической трансформации объектов ракетно-космической техники.