Программный комплекс для решения задач математического моделирования процесса изотермической вулканизации

К настоящему времени установлены общие закономерности серной вулканизации диеновых каучуков, основанные на существовании в композициях действительных агентов вулканизации эластомеров (ДАВ). Однако принципы эффективного проведения процесса с использованием многокомпонентных структурирующих систем изучены недостаточно. Описание механизма их действия осложняется многообразием взаимодействий компонентов и влиянием каждого из них на кинетику вулканизации. Это приводит к различным рецептурно-технологическим усложнениям реальной технологии и сказывается на качестве и технико-экономических показателях производства резинотехнических изделий. Анализ кинетики вулканизации показал, что существующие подходы к ее описанию основываются на химических реакциях макромолекул с вулканизующими агентами, а параметры образования пространственной сетки вулканизаторов зависят от множества факторов, влияние которых можно оценить только с помощью специального математического и алгоритмического обеспечения [1]. Для повышения эффективности исследования, выявления причин, приводящих к получению продукции, не отвечающей нормативным требованиям, прогноза протекания процесса необходимо создание специального программного обеспечения (ПО).

Целью настоящей работы является разработка программного комплекса для решения прямой и обратной кинетических задач процесса изотермической вулканизации.

Системный анализ процесса вулканизации

Анализ известных теоретических подходов к описанию вулканизации, а также других процессов в химической промышленности [2–4] и аспектов их практической реализации с учетом особенностей отдельных стадий позволил выявить общие системные свойства и основные закономерности процессов и определить направление исследований для получения новой информации по оптимизации режимов вулканизации и свойств готовых изделий [5].

Системный анализ включает интегрирование различных методов и приемов исследования (математических, эвристических), разработанных в рамках различных научных направлений в единую взаимосвязанную совокупность методов.

Многофакторный анализ процесса позволил разработать общую структуру исследования (рисунок 1). Объект исследования является слабоструктурированным, поскольку содержит как качественные элементы (эластомеры, наполнители, условия проведения процесса) так и малоизученные (многокомпонентные структурирующие системы, неконтролируемые возмущения), которые имеют тенденцию доминировать. В состав общей структуры входят элементы, которые необходимо теоретически обосновать (кинетическая модель, процессы тепломассопе-реноса, оптимизация режимов, процессы переработки). Таким образом, для оценки способов решения необходимо определить все существующие взаимосвязи и установить их влияние с учетом взаимодействий на поведение всей системы в целом.

Анализ общей структуры показал, что механические свойства вулканизатов определяются химическими реакциями макромолекул с вулканизующими агентами, а для оценки параметров пространственной сетки вулканизатов необходимо разработать специальное математическое и алгоритмическое обеспечение.

В результате проведенной стратификации изучаемого объекта выделены следующие основные подсистемы:

• 1)    анализ и учет термофлуктуационных явлений, обеспечивающих ускорение протекания химических реакций;

• 2)    кинетическая модель вулканизации;

• 3)    оптимизация режимов вулканизации, обеспечивающая получение требуемых механических свойств.

Математическое моделирование процесса изотермической вулканизации

Получение достоверной информации о протекании процессов сшивания эластомеров комплексными структурирующими системами, тесно связано с проблемами проектирования, оптимизации и управления режимами вулканизации в промышленности. Известно, что одним из традиционных способов описания формальной кинетики вулканизации является использование кусочно-определенных функций для отдельных стадий процесса: индукционного периода, структурирования и реверсии. Описание процесса в целом и расчет кинетических констант в настоящее время выполнен только для отдельных типов каучуков и вулканизующих систем [6]. Основные заключения о кинетике процесса основываются на модельных системах с низкомолекулярными аналогами эластомеров. В то же время полученные количественные данные не всегда возможно распространять на производственные процессы.

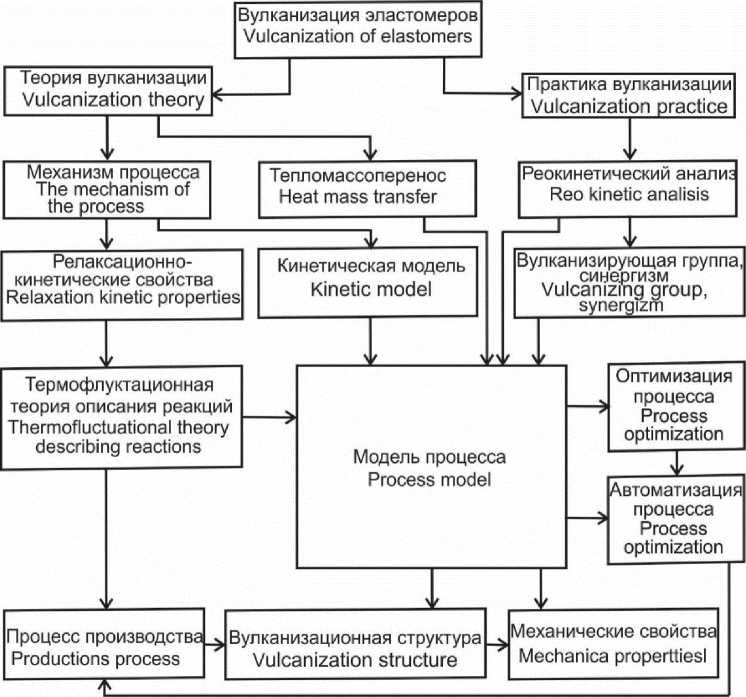
Рисунок 1. Схема исследования процесса вулканизации эластомеров

Figure 1. Scheme of study process of vulcanization of elastomers

Оценка физико-механических свойств производственных резин, по данным, полученным на предприятии, является, безусловно, прогрессивным методом в решении задачи моделирования процесса вулканизации, но требует строгого внутреннего единства физико-химического подхода на каждом этапе исследования и разработки вычислительных алгоритмов и программ.

Ответить на этот вопрос можно, только тщательно выполнив эксперименты [7, 8] по плану, соответствующему предполагаемой кинетической модели и рассчитав несколько альтернативных вариантов модели. Для этого требуется независимым методом установить число формальных механизмов реакций, ответственных за структурирование эластомерной композиции.

Традиционные методики анализа процессов во временной области не дают возможности четко разделять процессы с синергическим взаимодействием, что, в свою очередь, не позволяет использовать их для анализа производственных резин.

При решении задачи уточнения общей схемы химических превращений целесообразно исходить из максимального в некотором смысле механизма. Поэтому в кинетическую схему включены дополнительные реакции, описывающие образование и деструкцию лабильных поли-сульфидных связей (Vulab), внутримолекулярную циклизацию и другие реакции, приводящие к модификации макромолекул, образование макрорадикала и его реакцию с подвесками ДАВ.

Система дифференциальных уравнений (ДУ) по стадиям процесса будет иметь следующий вид [5]:

dC A I dt = - k_x • C a — k ₄ • C a - C . , dC_B I dt = k , • C_A - k ₂ • C_B + + в • k 4 • C a - C . + k ‘- C_R., dC_B . Idt = k ₂ • C_B - ( k ₃ + k ₅ + k ₇) • C_B . +

• -vk С -к С C

• ^{+ Л}6 C VuLab   4 Д C A C B * ,

dCv„ J dt = a • k • C„.,

VUSt                3B dCvuLab I dt = Y • k5 • CB - k6 • CvuLab,

dC_r I dt = 5 • k₇ • C „.

C                7

dCR. Idt = k8 • CR -k‘• CR., dCB I dt = -k8 • C„. R             8

Начальные условия:

Ca (0)=S •[ S8 ]•[ Ac ]•[ Akt ]6 •[ Cr (0)]’;

C b ( 0 ) = 0;    C b * ( 0 ) = 0;    C„ ( 0 ) = 0;

C™ ( 0 ) = 0; C c ( 0 ) = 0; C r ( 0 ) = 4,95;

^C r * ( 0 ) = C R ( ° ) ’ .

где ς , θ , η , – коэффициенты, [ S 8 ] – начальная концентрация серы, [ Ac ] – начальная концентрация ускорителя, [ Akt ] ^θ – начальная концентрация активатора (оксида цинка), [ С R (0)] ^η – начальная концентрация макрорадикалов. Здесь A – действительный агент вулканизации; В – предшественник сшивания; В* – его активная форма; С – внутримолекулярная связанная сера; VuSt, VuLab – стабильные и лабильные узлы вулканизационной сетки; R – каучук; R* – макрорадикал каучука в результате термофлуктуационного распада; α, β, γ и δ – стехиометрические коэффициенты, k 1 , k 2 …, k 8 , k 9 (k 8 ’) – константы скорости реакции, относящиеся к соответствующим стадиям процесса.

Прямая задача кинетики (ПЗК) – задача нахождения концентрации вулканизационных узлов как функции времени. Решение ПЗК сводится к решению системы ДУ (1) при заданных начальных условиях. Кинетическая кривая процесса вулканизации определяется по величине крутящего момента M ( t ) . Обратная задача кинетики (ОЗК) – задача идентификации констант скорости реакций, стехиометрических коэффициентов и переменных в системе (1). Решение ОЗК осуществляется путем минимизации функционала:

Ф (ki, k2,..., k8, k‘, а,в, 5,6, ’) = tк(2)

• = J q ² ( k i , k 2 ,..., k 8 , k ‘ , a , p , q , e , ’ ,t ) dt 0

q (kv k2,..., k8, k‘ ,a,l,^,6, ’, t ) = где, (3)

= R • [ M ( t ) - M min ] / ( M max - M m_m ) - C_Vu

M , M – соответственно максимальное и maxmin минимальное значения M (t). R - масштабный коэффициент.

Описание программного обеспечения

Программное обеспечение «Изотермическая вулканизация» разработано в качестве комплекса прикладных программ (КПП) для решения задач, связанных с математическим моделированием процесса изотермической вулканизации.

Для решения системы ДУ в пакете предусмотрены численные методы, включающие в себя:

• –    метод Рунге-Кутта четвертого порядка;

• –    метод Адамса.

Решение обратной кинетической задачи сводится к оценке констант скоростей реакций, стехиометрических коэффициентов и переменных в системе ДУ (1).

Для минимизации функционала (2) в пакете программ на усмотрения пользователя могут использоваться следующие методы: покоординатного спуска, Хука-Дживса, Розен-брока, Пауэлла, Нелдера-Мида, усреднения координат (с использованием элементов случайного поиска). Градиентные методы (первого порядка): наискорейшего спуска, сопряженных направлений (Флетчера-Ривса), переменной метрики (Давидона-Флетчера-Пауэлла), параллельных градиентов (Зангвилла).

На рисунке 2 изображена структурная схема, разработанного программного обеспечения.

Процесс идентификации констант скорости реакций, коэффициентов уравнений и стехиометрических коэффициентов осуществляется в несколько этапов:

• –    оцифровка реограмм;

• –    перевод крутящих моментов в концентрации;

• – определение начальных концентраций;

  – определение значений искомых параметров констант обеспечивающих минимум функционала (2).

Оцифровка реограмм может происходить вручную или же в автоматическом режиме с помощью, интегрированной в пакет, программы Gr2Digit.

Обработка экспериментальных данных может осуществляться как для одного измерения, так и набора (до 6 реограмм).

Перевод крутящих моментов в концентрации узлов вулканизационной сетки осуществляется следующим образом:

– значения крутящих моментов переводятся в условные единицы:

M =(M -M . A/(M -M . ) (4) усл       тек      min        max      min

– затем условные единицы переводят в (моль/кг), путем умножения M усл на масштабный коэффициент R .

Определение начальной концентраций C_a ( 0 ) ДАВ осуществляется по формуле:

Ca (0) = ^ •[S8]•[Ac]•[Akt]6 .[Cr (0)]’  (5)

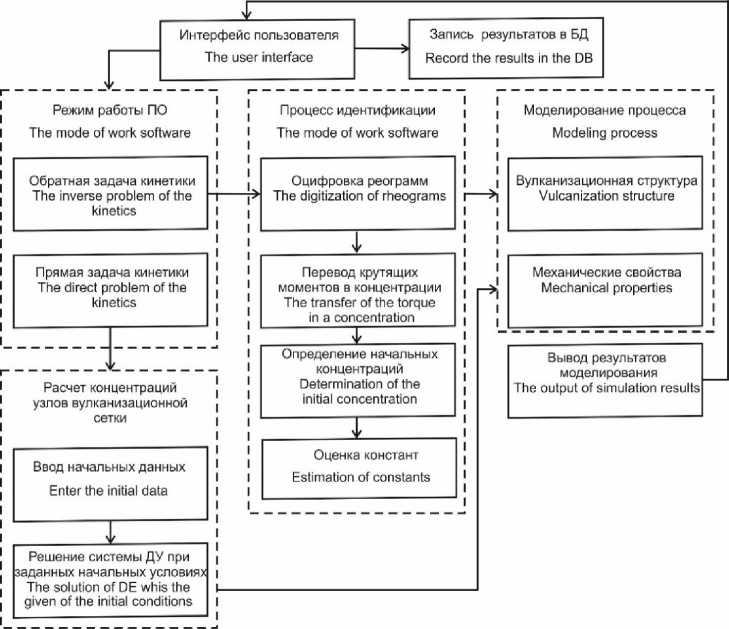
Рисунок 2. Структурная схема программного обеспечения

• Figure 2.    Structural software scheme

Апробация разработанного программного обеспечения

В качестве исходных данных использованы реометрические кривые, полученные при следующих начальных условиях:

• 1.    Значение концентрации серы в смеси: [S 8 ] = 0,0078 моль/кг.

• 2.    Концентрация ускорителя:  [A c ] =

  0,0019 моль/кг.

• 3.    Концентрация активатора: [ Akt ]^θ = 0,0012 моль/кг.

На рисунке 3 приведены экспериментальные и расчетные значения концентрации вулканизационных узлов, полученные в результате решения ОКЗ. В таблице 1 приведены рассчитанные значения констант скоростей реакций, в таблице 2 – оцененные значения стехиометрических коэффициентов и параметров модели.

Таблица 1

Значение констант скоростей реакций

Table 1

The value of the reaction rate constants

Константа Constant	Значения Values	Константа Constant	Значения Values
k1	0,12	k6	0,553
k2	0,1	k7	0,96
k3	4,8×10-20	k8	1,213
k4	1,213	k8'	0,21
k5	1,89×10-20	–	–

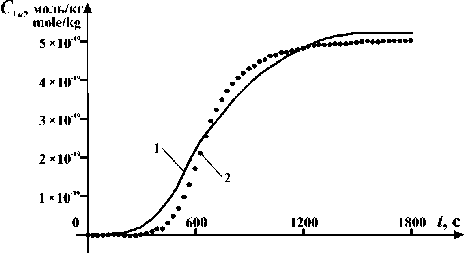
Рисунок 3. Изменения концентраций узлов вулканизационной сетки во времени.

• Figure 3.    Changes in the concentrations of the vulcanization grid points in time. 1 – the calculated values; 2 – experimental values.

Оцифрованные и обработанные экспериментальные данные заносятся в программу, определяются начальные приближения и диапазон поиска констант, после чего выбирается метод оптимизации.

Таблица 2 Значения стехиометрических коэффициентов и параметров модели

Table 2

The values of stoichiometric coefficients and parameters of the model pas

α	β	γ	δ	ξ	θ	η
1,21	1,4	1,02	1,9	1,65×108	0,97	-4,11

Заключение

На основе системного анализа теоретических подходов к описанию вулканизации усовершенствована общая структурная схема исследования данного процесса. Математическая модель процесса вулканизации дополнена начальными условиями, которые определены как функции исходных концентраций компонентов вулканизующей группы. Для решения обратной кинетической задачи предложены дополнительные критерии качества модели. Разработан программный продукт, предназначенный для проведения научно-исследовательских работ при изучении процессов вулканизации резиновых смесей