Прогрессирующее формоизменение дисков при теплосменах без механических нагрузок

[minГ (or -Оe))A^r + (о„ — Оe))Af„ 1 dv + I" min(oS -Ore))au'dS < 0.(1)

т L^        y^^/^j vS

Здесь σr, σφ – напряжения на поверхности текучести материала, связанные с приращениями пластических деформаций Δεr, Δεφ ассоциированным законом течения; σr(e) , σϕ(e) – температурные напряжения, вычисленные в предположении идеальной упругости материала, σS – расчетный предел текучести материала [1], v – объем диска, ∆u׳ – разрыв приращения радиального перемещения на поверхности Sµ.

Условия совместности приращений пластических деформаций и перемещений за цикл имеют для диска вид [2]

d ( A u )          A u

AE = ^7"^, А£ф = —.

drr

Изображенному на рис. 1, а мгновенному распределению температур соответствуют термоупругие напряжения [2]

e e aEt                               (      Гr or-^--H1 - Pi) при 0 < P < Pi \p=-, Pi = -11, 2                          V    RR

(a a Et p 2i. ₂\ (a     a Et p^г

a ⁽ ) = —^ ( 1 - p^L ) , a ^=—— ^ ( 1 + p² ) при p i < p < 1.

2 p2                     2 p2 x7

Рис. 2 иллюстрирует изменение этих напряжений по радиусу при различных значениях ρ 1 (т.е. в разные моменты времени цикла) при положительном перепаде температур (рис. 1, а ). Радиальным и окружным напряжениям соответствуют сплошные линии на рис. 2; штриховыми линиями показано объемлющее распределение. Максимальное значение радиальных и минимальное значение окружных напряжений достигаются в каждой точке диска одновременно – в момент прохождения через нее теплового фронта ( ρ = ρ ₁). Разность этих напряжений больше каждого из них:

max ( O re - 0 Г ) = a Et ,

^{T                  7}              .       (4)

min ( O r^e ) - a ^,e ) ) = 0.

При действии температурного поля, изображенного на рис. 1, б , напряжения отличают-

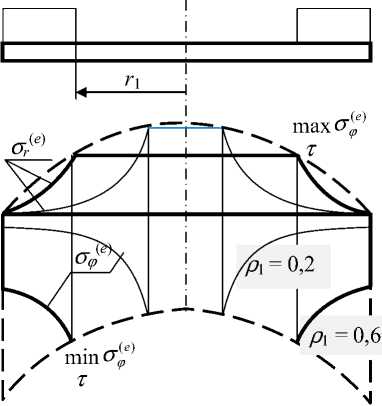
Рис. 2. Термоупругие напряжения в пластине в разные моменты времени

ся от представленных на рис. 2 только знаком. При этом max (are)- o^,e )) = 0.   min (ar e)- a^,e )) = -aEt.

TT

В соответствии с приближенным кинематическим методом теории приспособляемости примем, что приращения за цикл остаточных радиальных перемещений в диске при t ≥ 0

C

Au = , C = const, C < 0.(6)

r

Тогда в соответствии с (2)

C C

A^r =—5-, Ae„ = —, AEr > 0.(7)

r2

При условии текучести Треска–Сен-Венана max( |ar|,|a^|,|ar -a^|) = a5(8)

приращениям пластических деформаций (7) соответствуют (согласно ассоциированному закону течения) напряжения на поверхности текучести ar - av = as.(9)

Подставляя в баланс работ (1) соотношения (7), (9) и (4), получим верхнюю оценку условий начала прогрессирующего формоизменения:

aEtf = as.(10)

Здесь t f – значение температуры t , при котором начинается прогрессирующее формоизменение. Нетрудно доказать, что эта верхняя оценка совпадает с точным решением, поскольку при напряжениях (3), условии (10) и нулевых значениях, не зависящих oт времени остаточных напряжений, выполняются все требования статической теоремы теории приспособляемости [1].

Таким образом, в диске из материала с несущественным деформационным упрочнением повторные перемещения по радиусу границы нагретой периферийной зоны приводят при условии

Механика

(10) к прогрессирующему перемещению всех точек в направлении центра диска (уменьшению любого заданного радиуса r по закону (6)). При этом вследствие пластического деформирования ликвидируются любые имевшиеся ранее остаточные напряжения. Из условия несжимаемости материала при пластическом деформировании следует, что при этом толщина диска не меняется.

В качестве примера отметим, что при рассматриваемых здесь воздействиях для диска из стали 12Х18Н9 (коэффициент линейного теплового расширения α = 18,2 1/град, модуль упругости E = 165 ГПа, расчетный предел текучести σ s = 118 МПа при температуре 500 °С) температурный перепад начала прогрессирующего формоизменения t f составляет 40 °С. С уменьшением расчетного предела текучести эта величина уменьшается.

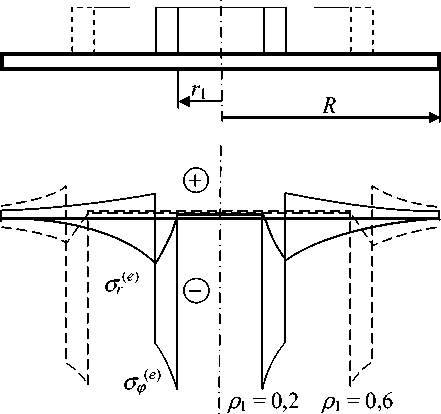
Рис. 3. Термоупругие напряжения при движении тепловой волны

Следует отметить, что приращения остаточных перемещений и деформаций за цикл (6) и (7) соответствуют движению изображенного на рис.1, а температурного фронта по всему диску – от центра до периферии. Очевидно, что в центральной части диска такое поле температур не может существовать по условиям теплообмена. Чтобы приблизить условия нагружения диска к реальным, примем, что в центральной части диска с радиусом a температура не изменяется в течение цикла, а приращения перемещений здесь равны нулю. С учетом разрыва приращений перемещений из (1) тогда следует, что

При повторных перемещениях границы между холодной периферией и горячим центром диска результаты аналогичного расчета отличаются только знаком константы С в (6), т.е. при перепаде температуры, превышающем определенный из (10), имеет место прогрессирующее увели- чение радиуса диска.

Рассмотрим теперь циклические воздействия тепловой волны, изображенной на рис. 1, в . Термоупругие напряжения в этом случае могут быть вычислены как комбинация решений для полей, изображенных на рис. 1, а и б . С учетом обозначений, показанных на рис. 1, в , получим

(a    (a a Et ( 2    2 a                      (     r r )

°,=P2 - Pi) при 0 ^ p^ Pi Ip=-• Pi = |.

2           ^ RR)

При P i ^ P ^ P 2

e    aEt or) =

i -

4-(P2 -P) •

(e)     a Et

°ф      2

_ 2

1+p2-(p2-p2).

ПРИ P2 ^ P^ i

(_e)_ ^{a E}tl Л   2^ ^{- p} 2     ( e ) _^{a E}t/ л   2U ^{+ pP}

^r =  2“ (p2 - pi ) -p^, Оф = — (p2 - pi ) -^2- .

Распределение этих напряжений по радиусу диска иллюстрирует рис. 3 для двух значений ρ 1 при ρ 2 – ρ 1 = 0,1. Максимальное значение разности радиальных и окружных напряжений (превышающее максимальные значения каждой составляющей) достигается на внутренней стороне горячей волны:

max (ore) - ty;(,e)) = aEt, и условие начала прогрессирующего формоизменения для «узкой» волны, когда р2 - pi << i, практически совпадает с (10). Однако в отличие от движущегося теплового фронта, минимальное значение разности термоупругих радиальных и окружных напряжений не равно нулю; оно достигается в холодной зоне на внешней границе горячей тепловой волны:

m _τ ax ( σ _r ^{( e )} - σ_ϕ ^{( e )} ) = - α Et ^{ρ 2} ₂ ^{ρ 1} .                             (12)

В результате в небольшой центральной части диска реализуется знакопеременное неупругое деформирование, начинающееся раньше, чем прогрессирующее формоизменение. Как и в случае движения теплового фронта, особенности решения в центре диска исчезают, если принять, что в центральной части температура постоянна в течение цикла. Можно, по-видимому, ожидать, что при одинаковых максимальных температурах повторные проходы тепловой волны приведут к меньшим остаточным перемещениям, чем проходы теплового фронта. Количественная оценка различий требует расчета кинетики неупругого деформирования.

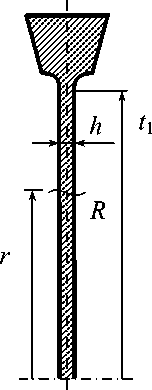
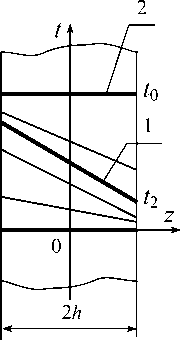
В рассмотренных примерах необходимое условие существования прогрессирующего формоизменения (неизохронность неупругого деформирования [1]) выполнялось за счет движения зоны действия максимальных напряжений. Покажем теперь, что накопление остаточных перемещений и деформаций при теплосменах без механической нагрузки возможно даже при однопараметрических тепловых воздействиях, если температурно-временная зависимость свойств материала приводит к неодновременности неупругого деформирования по объему диска. Диск постоянной толщины 2h с жестким ободом, изображенный на рис. 4, а, подвергается повторным нагревам и охлаждениям с линейным распределением температуры по толщине в каждый момент времени цикла (рис. 4, б) при равномерном нагреве обода до средней температуры диска. На кратко- временных режимах нагрева и охлаждения перепад температуры по толщине отличен от нуля (температуры в разные моменты времени иллюстрируют тонкие линии на рис. 4, б, максимальному значению перепада Δt = t1–t2 соответствует линия 1). При этом расчетный предел текучести σS (равный пределу прочности материала [3]) остается постоянным, а термоупругие напряжения

( e )     ( e ) α E ∆ t ( τ ) z

σr =σϕ = 2(1-µ) h .

На длительном стационарном режиме температура t 0 постоянна по толщине (линия 2 на рис. 4, б ) и термоупругие напряжения отсутствуют, а предел длительной прочности σ Sτ меньше, чем σ S .

а)

б)

в)

Рис. 4. Прогрессирующий изгиб диска

Предположим, что приращения прогибов диска за один стабильный цикл распределяются как показано на рис. 4, в :

.           . I л Г

.

∆w = ∆w 1 -

01 R

Им соответствуют приращения радиальных и окружных неупругих деформаций

Механика

∆ ε _r = - z

d ² ( ∆ w )

dr ²

≡ 0,   ∆ ε_ϕ

-

z d ( ∆ w ) z ∆ w ₀ r dr r R

.

На цилиндрической поверхности r = ных перемещений за цикл на величину

R, –h ≤ z ≤ h имеет место разрыв приращений радиаль-

∆ w ∆ u ′ = - z ⁰ .

R

Соотношение (1) принимает тогда вид

Rh

J r 1 min ( 0 - h ^L

e z ∆ w σ_ϕ sign z - σ_ϕ ^{( )} )     ⁰

rR

h

1         "      Г,                     ,          Мл, dz + R 1 mjn (^ sign(-z)- а())I -z^0 I

-         - h     L                         v /_

h

dz ≤ 0. (17)

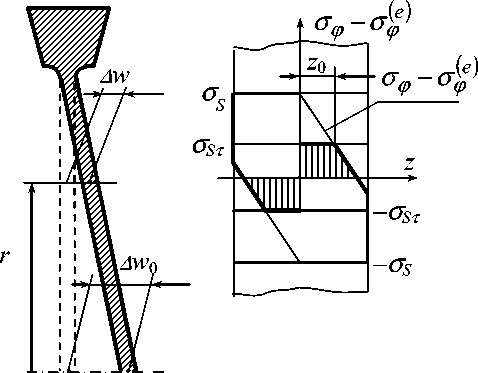
Определение значений разности окружных напряжений на поверхности текучести σφsignz при условии текучести Треска–Сен-Венана и термоупругих напряжений σφ(e), которые доставляют минимум первому подынтегральному выражению в (17), иллюстрирует рис. 4, г. В приповерхностных слоях диска (при |z| ≥ z0) они достигаются (т.е. реализуется неупругое деформирование) на кратковременном переходном режиме при достаточно больших максимальных термических напряжениях. В остальной части неупругое деформирование реализуется в виде ползучести на стационарном режиме.

В зоне разрыва приращений перемещений (16) минимальное значение второго подынтегрального выражения в (17) достигается всюду на стационарном режиме. Таким образом, выполняется необходимое условие существования прогрессирующего накопления остаточных перемещений: неизохронность неупругого деформирования. Из соотношения (17) после подстановки значений напряжений, показанных на рис. 4, г , следует достаточное условие:

(1 -a)3 3                           αE∆tf                     σ q+     2 - (1+a)≥0, q≥1-a, q=             , ∆tf =t1 -t2, a= S .

2 q     2                        2 ( 1 - µ ) σ _S                   σ _S

Зависимость предельного перепада температуры от величины a иллюстрирует рис. 5. Для сравнения отметим, что условие реализации знакопеременного течения имеет вид [3]

α E ∆ t_f

⁺ σ 0,2/ ,

^≥ σ 0,2

2 ( 1 - µ )     ^0,2

где σ 0,2 – предел текучести, а σ 0,2/ τ – предел ползучести при длительности выдержки в одном цикле. Очевидно, что при характерной для повышенных температур небольшой разнице величин σ S , σ 0,2 , σ 0,2/ τ прогрессирующее формоизменение реализуется при меньших перепадах температуры, чем знакопеременное течение.

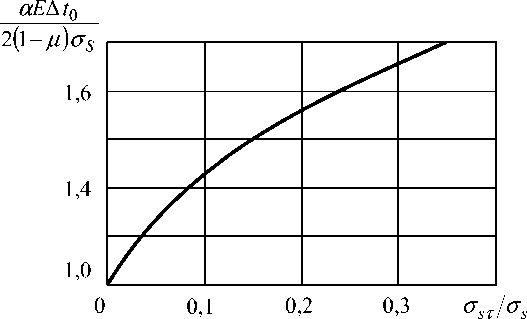
Рис. 5. Зависимость предельного перепада температуры от величины σ _S σ _S

Рассмотренные особенности накопления остаточных перемещений и деформаций могут оказывать существенное влияние на работоспособность дисков газотурбинных установок, подов нагревательных печей, плоских днищ термонапряженных сосудов.