Прохождение электромагнитной волны через прямоугольный волновод с активной прямоугольной пленкой

На настоящее время известно несколько практически реализуемых структур полупроводниковых РАЭ. В основе взаимодействия известных структур с электромагнитными волнами лежит поперечный или продольный дрейф зарядов. Типичным примером структуры с продольным дрейфом зарядов является несимметричная микропо-лосковая линия передачи на полупроводниковой подложке с профилем легирования в поперечном сечении, характерным для дискретного диода Гана [7]. Вдоль направления распространения волны прикладывается внешнее однородное статическое электрическое поле, создающее в подложке область с отрицательной дифференциальной проводимостью. Описан также другой вариант РАЭ на основе щелевой линии передачи с прямоугольным экраном с полупроводниковой пленкой с поперечным дрейфом [1; 5–7; 10].

Одним из основных недостатков активных полосковых линий передачи с распределенными параметрами в СВЧ- и КВЧ-диапазонах является небольшой коэффициент усиления [7], что приводит к увеличению размеров и уменьшению КПД. Коэффициент усиления структуры можно увеличить, если в подложку ввести слой из ферримагнитного материала с поперечным подмагничиванием в плоскости слоя [1]. Ниже построена линейная теория активных волноведущих структур с полупроводниковыми пленками с поперечным дрейфом носителей заряда и намагниченными ферримагнитными слоями, объясняющая механизм увели- чения коэффициента усиления таких структур. В качестве иллюстрации возможностей теории проведен электродинамический анализ различных волноведущих структур с активными полупроводниковыми пленками и намагниченными ферримагнитными слоями.

Прямоугольный волновод с активной полупроводниковой пленкой с поперечным дрейфом носителей заряда и намагниченными ферритовыми слоями

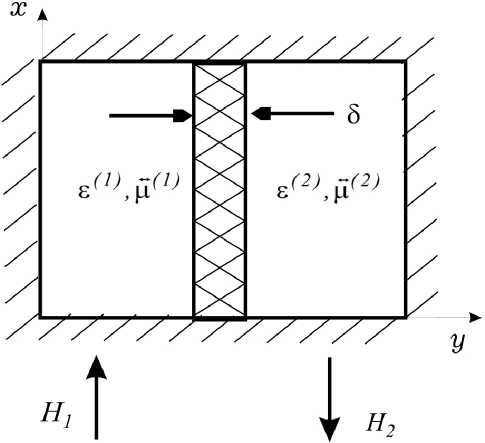
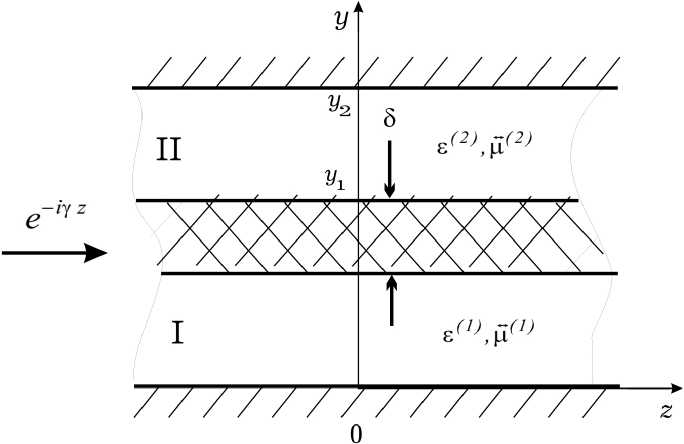
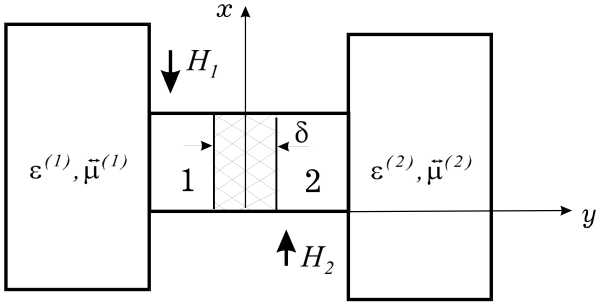
Рассмотрим H { E y , H x , H z }-волны в двумерной слоистой структуре (зависимость вдоль оси x отсутствует) – с полупроводниковой пленкой (тонкий n-GaAs слой) с отрицательной дифференциальной проводимостью, расположенной между ферримагнитными слоями, подмагниченными вдоль оси x (см. рис. 1, б ). Слои из ферромагнита располагаются между плоскостями, выполненными из металла, который обладает идеальной проводимостью. Такого типа структуры – это модели прямоугольного волновода для волн Н-типа (рис. 1, а ).

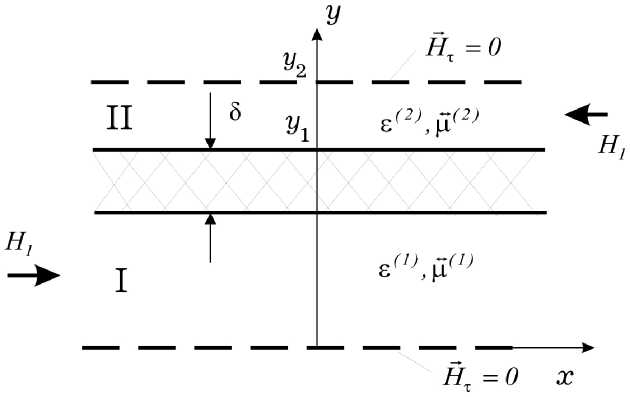
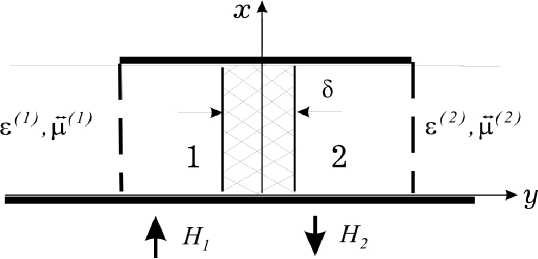
Двумерная слоистая структура с магнитными (импедансными) стенками, поперечное сечение которой изображено на рис. 2, а , моделирует более сложные полосково-щелевые структуры: несимметричную полосковую линию с полупроводниковой пленкой, расположенной между двумя намагниченными ферримагнитными слоями в обычном прямоугольном волноводе (рис. 2, б ) и в сложном прямоугольном волноводе (рис. 2, в ).

а                                                    б

Рис. 1. Активные линии передачи с полупроводниковыми пленками и ферритовыми слоями: а – поперечное сечение прямоугольного волновода; б – плоская активная структура

Fig. 1. Active transmission lines with semiconductor films and ferrite layers: a – cross-section of a rectangular waveguide; b – flat active structure

Полупроводниковый слой в активных волноведущих структурах с поперечным дрейфом носителей заряда в реальных приборах имеет малую толщину. Дифференциальная проводимость по- лупроводника при приложении сильного статического электрического поля Е0 вдоль оси x на рис. 2, б (для n-GaAs, Eo ~ 3,5 кВ/см) становится отрицательной, и появляется возможность усиления электромагнитных волн. В общем случае

б

в

Рис. 2. Поперечное сечение активных волноведущих структур с ферримагнитными слоями: а – плоский волновод c полупроводниковой пленкой и магнитными (импедансными) стенками; б – микрополосковая линия передачи с полупроводниковой пленкой; в – Н-волновод с полупроводниковой пленкой (штриховые линии обозначают магнитные стенки

Fig. 2. Cross section of active waveguide structures with ferrimagnetic layers: a – plane waveguide with semiconductor film and magnetic (impedance) walls; b – microstrip transmission line with semiconductor film; c – H-waveguide with a semiconductor film (dashed lines indicate magnetic walls

проводимость активного слоя является анизотропной, т. е. обладает различными свойствами в зависимости от направления распространения волны. Статическое поле E ₀ (поле смещения) в такой структуре имеет гетерогенное распределение по x координате . Данное распределение связано с тем, что в пленке из полупроводника образуются домены, которые статичны. В данном разделе статьи физические особенности статического поля в гомогенной структуре учитываться не будут.

При распространении электромагнитной волны вдоль оси z в полупроводниковом слое появляется электрический ток с плотностью j. Зависимость распространения по координате z и времени t выражает комплексная постоянная распространения: exp{iюt - iуz}; Y = Y‘ — iy"-

В линейном (малосигнальном) приближении в полупроводниковом слое будет возникать ток с плотностью j = aE, где с - дифференциальная проводимость полупроводника. Следует учесть, что волны пространственного заряда и анизотро- пия проводимости полупроводника не учитываются.

Влияние, которое оказывает тонкий полупроводниковый слой на распространение электромагнитных волн в структуре, учитывается путем введения на поверхности y = y i (рис. 1, б ) линейного электрического тока:

—*            —*

J т =5— E т ,

где нижний индекс т - это касательные составля

ющие к плоскости у = у 1 соответствующих векторов.

На рис. 1 и 2 представлено поперечное сечение активных волноведущих структур с ферримагнит-

В предельном случае при ц^ = ц ^²) = 0, дисперсионное уравнение (4) переходит в соотношение для плоской активной структуры с изотропными слоями:

ными слоями.

В дальнейшем исследуем и рассчитаем подоб-

ные структуры.

Из приведенных данных имеется возможность получить модель расчета для волноведущей линии передачи с активной полупроводниковой пленкой, которая изображена на рис. 1, б : для линии передачи с намагниченными ферритовыми слоями и линейным электрическим током (1) на гра

r ⁽¹⁾ m         r ⁽²’         ₍₂₎

——- ctg(г(1)уг) + —— ctg(г(2)(у2 - уг)) - к ц(1)                 к ц(2)                                         (5)

- i 4 л к 5— = 0, ю

где r ⁽ n ) = V к ² s⁽ n М n )

-у ² , ( n = 1,2).

нице у = у ₁.

Так как электрический ток (1) на границе у = у 1 не изменяет граничных условий для тангенциального электрического поля на этой границе, то для Н-волн можно записать следующие граничные ус

ловия при у = у 1' .

E CD = e (²⁾ , н (D - н (2) = 4 л —5 e (ц                  (₂)

xx  zz   x

c где с – скорость света.

Намагниченные I и II ферритовые слои представленные рис. 1, б можно охарактеризовать тензорами магнитной проницаемости ц ⁽ n ) ( n = 1,2) (оси гиротропии направлены вдоль оси x ) [3]:

Следуя из численного анализа уравнения (4), видим, что мнимая часть комплексной постоянной распространения волн у" ( у = у' - i у" ) структуры с ферримагнитными слоями для одного из направлений больше мнимой части постоянной распространения волн структуры с гомогенными слоями, если при этом прочие условия одинаковы.

Докажем это утверждение для частного случая структуры на рис. 1, б . Пусть у 2 = 2 у 1 и ферромагнитные слои 1 и 2 имеют одинаковые физические параметры, но подмагничены в противоположных направлениях: ц ⁽¹⁾ =ц ⁽²⁾ =ц ,

ц

(1) =

a

-ц

a

= ц a ,

Г 10   0

^{ц (} n ) = 0

ц ⁽ n )

_Б ⁽¹⁾

= s ⁽²⁾=s о о .

V

a

ц ⁽ n )

где ц ⁽ n ) - диагональный элемент тензора ц ⁽ n ); ц О* ) - недиагональный элемент тензора ц ⁽ n).

В предположении отсутствия вариации поля

вдоль оси x , для волн, распространяющихся вдоль оси z в структуре, изображенной на рис. 1, б , не-

трудно получить следующее дисперсионное урав-

нение:

(1)           ,            ,       „(2)

—— Ctg ( r ⁽¹⁾ у 1 ) + —— Ctg( r ⁽²⁾ ( у 2 ^- у 1 )) ^- к ц™    ^v      ' к ц ²

-

Y

k

( и (2) ^ц a

I^V2

и (1) ) ^ц a

|

- i 4 п к 5^—= ю

где

.______________________                       (ц(n) )2

r ⁽ n ) = Jк ² о ⁽ n ) ц ^ ) -у ² , ц ^ ) = ц ⁽ n ) - a ,

⁽ n )

( n = 1,2).

При смене направления распространения волны на противоположное в уравнении (4) необходимо (1)       (2)

сделать замену «+» на «-» перед ц' a' , ц a .

В этом случае уравнение (1) переписывается следующим образом:

к ² оц _± - у ² ctg | у ₁ к ² оц _± - у ² | +

^V                                                 (6)

+ -^a-у-iац । к = 0, ц где

—              ^(ц a )

а = 2 л к 5 — , ц, =ц--—— .

ю           ц

Уравнение (6) для случая а ^ 1, |ц a | ^ ц можно решить методом возмущения. Будем искать замедленные волны с постоянной распространения в виде у / к = у ₀ +у ₁ , где у ₀ = ^оц-л ² /(2 ку ₁ ) ² -нормированная постоянная распространения в структуре без полупроводниковой пленки при ц a = 0. Тогда для У 1 получаем выражение:

(ца)

J”

у ₁ =±-- i а ^ ± ( ц , ц a ) ,                         (7)

к 5y0 + ~ ц где функция

Г      ц Г¹

^р ± ( ц , ц a ) = ц ± | к 5y ₀ + — I

V          ^ц )

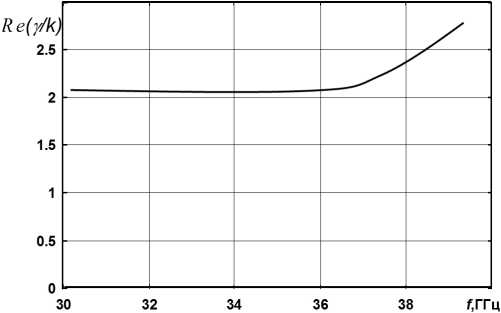
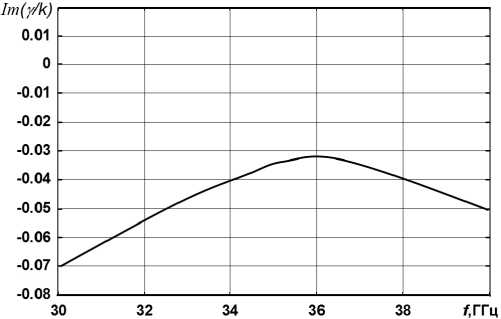
Рис. 3. Дисперсионные зависимости для плоской активной структуры с диэлектрическими слоями без потерь: y ₂ = 7,2 мм; y 1 = 3,4 мм; е ^{( 1 )} = 9; е ^{( 2 )} = 2; к 5 = 0,01; a / w = 1

Fig. 3. Dispersion dependences for a planar active structure with dielectric layers without losses: y 2 = 7,2 mm; y 1 = 3,4 mm; s ^{( 1}* = 9; е ^{( 2 )} = 2; к 5 = 0,01; a / w = 1

характеризует влияние гиротропии ферромагнитных слоев на коэффициент усиления волны в структуре; верхние знаки в (7) соответствуют распространению волны в прямом направлении, нижние знаки – распространению волны в обрат-

А =

„ ⁽¹⁾U^{(2) ц} 1 ^ц 1

„ (1) ^ц 1

—

„ (2) , ^ц 1

ном направлении.

Из формулы (7) следует, что в структуре существует невзаимный эффект усиления волны: в прямом направлении при ц a ^ 0 коэффициент усиления волны больше, чем в отсутствие гиро-тропии, в обратном - меньше. Например, для ферромагнитного слоя с толщиной к 5 = 1 и намагниченностью насыщения ферритов 4пM 0 = 0,4 ® / h 0 ( h 0 - гиромагнитное отношение) при внешнем поле H 0 = 0,1 ® / h 0 функции F + , F - , характеризующие усиление в линии, примерно равны 1,36 и 0,55. Для изотропных слоев при данном характеризующем усилении F + = F_— = 1. Получаемый эффект связан с явлением смещения поля, которое имеет место в ферромагнитных материалах. При рассматриваемом направлении намагничивающе-

^ц а      ^ц a

---.

LI (2)_U(2) ц(1)ц(1) ц ц ц ц i

е = е ⁽¹⁾ + е ⁽²) .

Соотношения (8) получены из уравнения (4) путем аппроксимации ctg( z ) ~ 1 / z + z / 3. Магнитные потери в ферромагнитных слоях были учтены с помощью задания мнимой и вещественной частей компонент тензоров магнитной проницаемости в форме Полдера [3; 4]: ц = ц' ^— i ц" , ц а =ц а ^— i ц а ,

ц' = 1 — ^ А ( 1 — ^ ² )( 1 + р ² ) ² — 2 р ² ( 1 + р ² )

_— 1

I ² А^{— 1} ,    (9)

го поля происходит смещение поля вдоль оси y , что показано на рис. 1, б .

Дисперсионное уравнение (4) численно исследовалось на ПЭВМ методом Дживса – Хука [9], в качестве исходного приближения для которого

ц" = р А ( 1 + ^ ² ) А^{— 1} ,

ц ; = ( 1 —; ² ■' ¹ .

_Ц;= 2 Рй ( 1 ₊ р ² ) ^— 2 а - ¹ ,

использовалась формула для постоянной распространения в виде [2; 8]:

2      7 7 /      7 \ 1

А = ( 1 — ^ ² ) + 4 ^ ² р ² ( 1 + р ² ) ,

1 1 k

—BA ±

to ^=— , ®

®

А = m

®

где

к 5

± Re ^

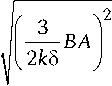
+ е---—+ i4пк 5— А > , ( к 5 ) 2          ®

L =± Im . к

—

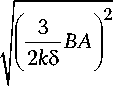
—-—+ i4пк 5^— А > , ( к 5 ) 2           ® I

® 0 = h 0 H 0 , ® m = ^h 0^{4 n} M 0 ,

где 4 п M_o - намагниченность насыщения феррита; H ₀ – напряженность поля подмагничивания; Р - параметр, учитывающий потери в феррите; h ₀ – гиромагнитная постоянная.

Часть итогов электродинамического анализа структуры (рис. 1, б ) представляется на рис. 3–8, а результаты сравнения частей комплексной

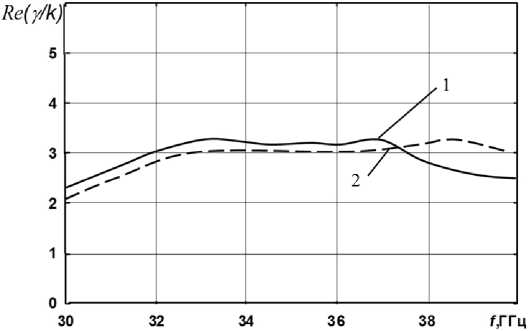
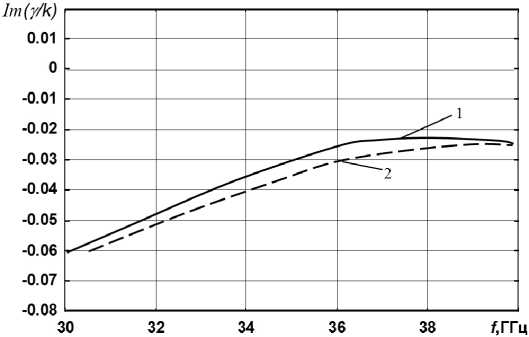
Рис. 4. Дисперсионные зависимости для плоской активной структуры с ненамагниченным ферритовым слоем с учетом потерь в феррите: y ₂ = 7,2 мм; y ₁ = 3,4 мм; ε ⁽¹⁾ = 10; ε ⁽²⁾ = 1; k δ = 0,01; σ / ω = 1; β = 0,1; кривые 1 – расчет по методу Дживса – Хука; кривые 2 – расчет по формуле (8)

Fig. 4. Dispersion dependences for a planar active structure with an unmagnetized ferrite layer taking into account losses in ferrite: y ₂ = 7,2 mm; y ₁ = 3,4 mm; ε ⁽¹⁾ = 10; ε ⁽²⁾ = 1; k δ = 0,01; σ / ω = 1; β = 0,1; curves 1 – calculation by the Jeeves–Hook method; curves 2 – calculation by the formula (8)

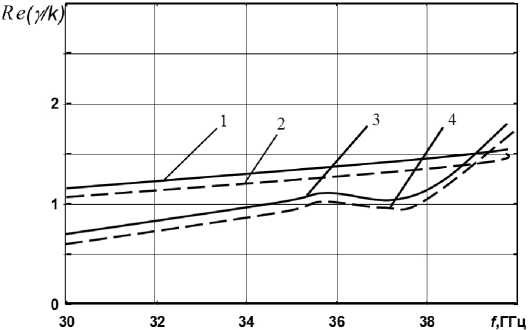
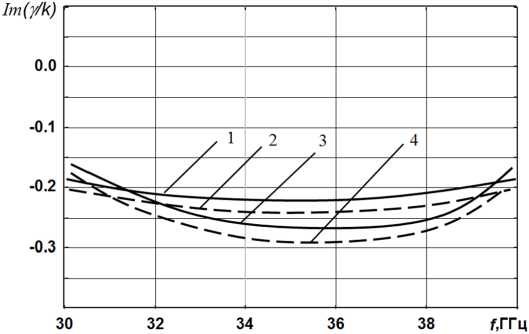
Рис. 5. Дисперсионные зависимости для плоской активной структуры c ферритовым слоем: кривые 1, 3 – прямое направление распространения волны; 2, 4 – обратное направление; кривые 1, 2 – расчет по методу Дживса – Хука; 3, 4 – расчет по формуле (8); 4 π M ₀ = 4 кГс; H ₀ = 1 кЭ; остальные данные приведены на рис. 4

Fig. 5. Dispersion dependences for a planar active structure with a ferrite layer: curves 1, 3 – forward direction of wave propagation; 2, 4 – reverse direction; curves 1, 2 – calculation by the Jeeves-Hook method; 3, 4 – calculation by the formula (8); 4 π M ₀ = 4 kG; H ₀ = 1 kOe; the rest of the data are shown in Fig. 4

постоянной распространения γ отражены на рис. 4–5. Действительные и мнимые части постоянной распространения γ были получены при помощи метода Дживса – Хука с использованием кривых, которые были вычислены по формуле (8). Как видно из рисунков, имеется хорошее качественное совпадение поведения дисперсионных характеристик [1].

На рис. 5–8 приведены результаты расчетов дисперсионной постоянной основной волны рассматриваемой структуры при различных значениях напряженности подмагничивающего поля H ₀ по методу Дживса – Хука.

Посмотрев на рис. 7, можно увидеть, что плоская активная структура имеет сильно выраженные невзаимные свойства в области ферромагнитного резонанса, а усиление (Im(у / к)) основной волны в прямом и обратном направлении в три- четыре раза различается. Помимо этого, значительно различаются и реальные (действительные) значения постоянных распространения Re(y / к). Данные свойства обусловлены распределением СВЧ–поля, которое различается в зависимости от изменения направления распространения поля. Это видно при рассмотрении прямой и обратной волны. Для прямой волны в направлении +z максимум поля будет смещаться к активной полупроводниковой пленке, а при этом для обратного направления максимум поля будет смещаться к металлическим стенкам прямоугольного волновода. Что касается зависимостей реальной части постоянной распространения Re(Y / к) от поля, то аналогичный характер они имеют для прямоугольного волновода с ферритовыми слоями без пленки [9]. Наиболее интересны в практическом смысле дисперсионные характеристики для пло-

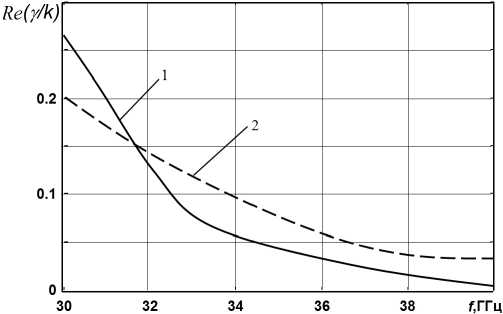
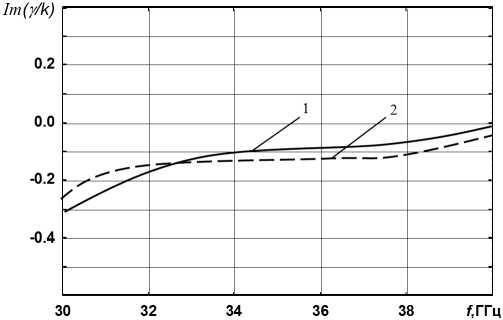
Рис. 6. Дисперсионные зависимости для плоской активной структуры c намагниченным ферритовым слоем, рассчитанные по методу Дживса – Хука: 4 π M ₀ = 4 кГс; H ₀ = 5 кЭ; кривые 1 – прямое направление; 2 – обратное направление; остальные данные приведены на рис. 4

Fig. 6. Dispersion dependences for a planar active structure with a magnetized ferrite layer, calculated by the Jeeves–Hook method: 4 π M ₀ = 4 kG; H ₀ = 5 kOe; curves 1 – forward direction; 2 – reverse direction; the rest of the data is shown in Fig. 4

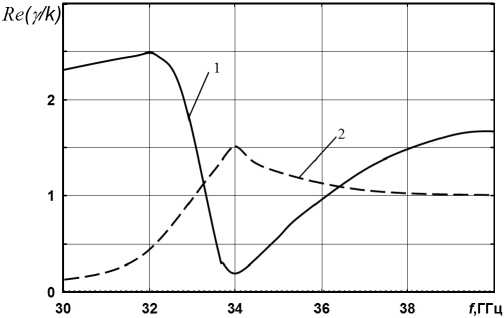
Рис. 7. Дисперсионные зависимости для плоской активной структуры c намагниченным ферритовым слоем, рассчитанные по методу Дживса – Хука: H ₀ = 12 кЭ; кривые 1 – прямое направление; 2 – обратное направление; остальные данные приведены на рис. 4

Fig. 7. Dispersion dependences for a planar active structure with a magnetized ferrite layer, calculated by the Jeeves–Hook method: H ₀ = 12 kOe; curves 1 – forward direction; 2 – reverse direction; the rest of the data is shown in Fig. 4

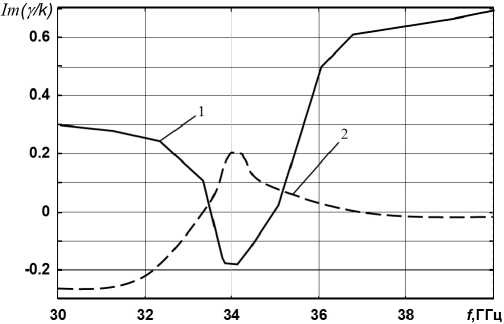
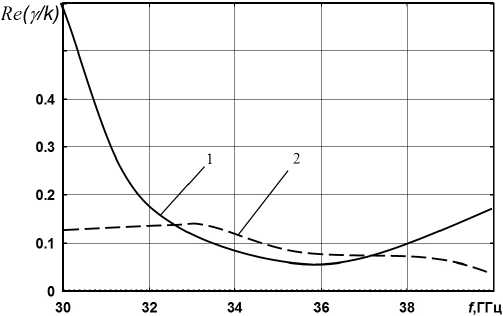
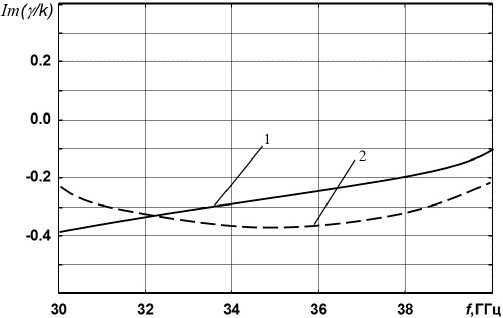
Рис. 8. Дисперсионные зависимости для плоской активной структуры c двумя намагниченными в противоположные стороны ферритовыми слоями ( ц^ = -Ц® , Ц ^{( 1 )} = Ц ^{( 2 )}): £ ⁽¹⁾ = £ ⁽²⁾ = 10; H о = 5 кЭ; 4 п M о = 4 кГс; кривые 1 - прямое направление; кривые 2 - обратное направление; остальные данные приведены на рис. 4

Fig. 8. Dispersion dependences for a planar active structure with two ferrite layers magnetized in opposite directions (ц^ = -Ц® , ц ^{( 1 )} = ц ^{( 2 )}): ^{£ <1)} = £ ⁽²⁾ = 10; H о = 5 kOe; 4 n M о = 4 kG; curves 1 - forward direction; curves 2 - reverse direction; the rest of the data is shown in Fig. 4

ской структуры с намагниченным ферритовым слоем при H ₀ = 12 кЭ в области ферромагнитного резонанса (рис. 7). При данной величине подмагничивающего поля усиление электромагнитной волны будет происходить только в одном направлении, при этом только в определенном частотном диапазоне. При обратном направлении распространения электромагнитной волны распространяющаяся волна будет затухать.

Заключение

В статье исследовано прохождение электромагнитной волны через двумерную регулярную активную волноведущую структуру с полупрово- дниковой пленкой с отрицательной дифференциальной проводимостью, расположенной между подмагниченными слоями. На основе анализа полученного в статье дисперсионного уравнения можно сделать вывод, что коэффициент усиления рассматриваемой линии передачи можно увеличить с помощью введения в нее намагниченных ферромагнитных слоев. Усиление происходит за счет смещения электромагнитного поля в такой структуре к полупроводниковой пленке.

Полученные в ходе исследования и расчета результаты статьи возможно использовать с целью конструирования активных усилительных устройств с распределенными параметрами, а также для дальнейшей миниатюризации РАЭ.