Прохождение электромагнитной волны через прямоугольный волновод с отрезком полупроводниковой пленки

В предлагаемой статье рассматривается волноведущая электромагнитная система, представляющая собой прямоугольный волновод с идеально проводящими стенками. На узкую стенку волновода ( у = a ) в интервале z от - L до L помещается отрезок активной полупроводниковой пленки (например, GаAs) с отрицательной дифференциальной проводимостью, как показано на рис. 1. Будем считать, что в прямоугольном волноводе в отсутствие полупроводниковой пленки распространяется только волна Н^ , а остальные высшие моды являются запредельными.

1. Постановка задачи

Рассмотрим задачу дифракции основной моды на такой неоднородности. Представим электрическое поле в волноводе в виде суперпозиции поля основной моды и поля, созданного токами на неоднородности [1]:

E x = A 0 sin r ₀( a - у)e i ^Y 0 z +                            (1)

где r = kk ² ец-у ² ; r 0 = y k 2 ^еЦ-У 02 ; k = ^ю / ^c ; ^e ,

ц - диэлектрическая и магнитная проницаемости среды, заполняющей прямоугольный волновод;

Y o - продольное волновое число для волны Н^ .

Полагая, что зависимость поля вдоль оси x от-

( д „)

сутствует = 0 , из уравнений Максвелла полу-

15 x   У чаем [2]:

Hz

1 ^d E x ik ц d у

Подставляя в последнее соотношение выражение (1), получим:

Hz

ik ц

(

- A ₀ r ₀ cos r ₀( a - у ) e ^{Y o}

<

-

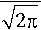
+да

J

-да

)

A ( у ) r cos r ( a - у ) e i ^Y z d у

J

+ —j=

N 2n

+да

J A ( y ) sin r ( a - y)e ^- i ^{Y z}d y ,

-да

Полупроводниковый слой в активных волноведущих структурах с поперечным дрейфом носителей имеет малую толщину: 5 ^ t , k n 5 ^ 1, где k_n – волновое число в полупроводниковом слое; t – характерный поперечный размер волноведущей структуры; 5 - толщина полупроводниковой пленки. Дифференциальная проводимость полупроводника при приложении сильного статиче-

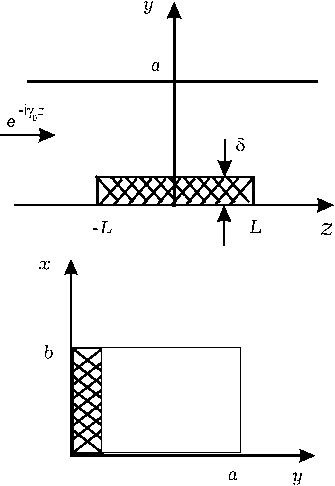
Рис. 1. Прямоугольный волновод с полупроводниковой пленкой конечной длины, расположенной вдоль узкой стенки Fig. 1. Rectangular waveguide with a semiconductor film of finite length along a narrow wall

которые следуют непосредственно из уравнений Максвелла.

Из уравнения (3) получаем, что

H (¹ =- H (²) +— E <²) .

^{z z}     ik § ^x

Подставим последнее выражение для Hz  в уравнение (4):

2H ( 2 )    ² _E( 2 ) i §

2 H; E ^z ik§ ^x    2 k

д 2    ,2

₂ ^{+ k £} H д z ²

E x 2 ) = 0,

которое после несложных преобразований приводит к следующему приближенному граничному условию для полупроводниковой пленки, лежащей на металле ( z e [ - L, L ]):

p (2)         (2) §2

E  - ik § H-- xz4

д2    /2

₂ ^{+ k £} П д z ²

E x 2 ) = 0.

Вводя обозначения:

E = E) 2 ) H = H ⁽ 2 )

Ex - Ex , Hz - Hz , перепишем граничное условие (6) в более удобном для нас виде:

ского электрического поля E ₀ вдоль оси x становится отрицательной, и появляется возможность усиления электромагнитных волн.

Полупроводниковую пленку в линейном приближении будем описывать с помощью двухсторонних граничных условий (1) при у = 0. Учитывая, что E ^ = 0 (касательное поле на металле) и отсутствует вариация поля вдоль оси x , из них следует ( р _п = 1):

E x ² ) - i^ н^ + H z ²)= 0, (3)

E_x - ik 3 H-- xz 4

д2    ,2

₂ ^{+ k Б} П д z ²

E x = 0.

Будем считать, что в силу малости толщины по лупроводниковой пленки § (kn§ ^ 1):

д 2Ui д z 2

= -Y 00 U i ,

н(2) н(1) i§

H z — ^H z — 2 k

где e_n

–

д ²     ,₂

2 ⁺ k ^£П д z ²

e X ² ) = 0,

комплексная диэлектрическая про-

ницаемость пленки, верхние индексы «1» и «2» указывают на принадлежность составляющих поля к той или иной области вне пленки (индекс «1» соответствует металлу, индекс «2» – волноводу).

При выводе граничных условий (3), (4) были использованы соотношения ( k = 1,2):

где Ui – какая-либо составляющая электромагнитного поля в структуре с отрезком полупроводниковой пленки. Тогда граничное условие (7) можно переписать в виде x z 4 'no x

где

22  2

' no = ^{k £} n ^Y 0 .

Группируя члены с E_x в последнем соотношении и проведя элементарные преобразования, получаем:

^E x = i n ^H z ,

где

i Гд e ^{( k} ) д e ^{( k} ) ^xz

/

Л

PkH ) = i yk

-

k §

д z

V

д x

)

,

s^{( k} ) e (k ) =

i ^f д H x ^k ) д h_Z ^k )

n= —2—

§ Z-2

^{1 -} T ^r no

.

— k

x

-

z

д z      д x

,

Формула (8) является приближенным эквивалентным граничным условием для полупроводниковой пленки толщины § с диэлектрической проницаемостью 8 _П, лежащей на металле.

Что касается волноведущей структуры с отрезком активной пленки (см. рис. 1), то для нее это граничное условие справедливо для плоскости у = 0 при z е [ — L , L ].

Таким образом, задачу дифракции волны прямоугольного волновода на отрезке полупроводниковой пленки малой толщины 5 мы свели к задаче дифракции волны Í ₁₀ на отрезке прямоугольного волновода, для одной из узких стенок которого справедливо импедансное граничное условие (8). Поэтому развиваемый ниже метод расчета тонкослоистых полупроводниковых неоднородностей справедлив для всех тех неоднородностей в прямоугольном волноводе, для которых можно записать соответствующие эквивалентные граничные условия типа (8).

L

ⁱ ( ^{7 7} 0 ) ^z

+ A 0 sin r 0 a e       dz .

— L

С учетом известного соотношения для дельтафункции 5 ( a ):

+да

J ei(7 7)zdz = 2^5(7 —7'), —да из (12) нетрудно получить выражение для коэффициента A(7):

A ( 7 ) = -^---

V 2n sin ra

L

J e x ( z ) e ⁷ z dz .

— L

2. Аналитический метод расчета продольных тонкослоистых неоднородностей в волноводных структурах

Определим функцию A ( 7 ) , которая фигурирует в интегральном представлении (1). Для этого подставим выражения (1) и (2) в уравнение (8) при y = 0; тогда мы можно записать следующее равенство ( z е [ — L, L ]):

Для улучшения сходимости интеграла в последней формуле перейдем от функции ex (z) к ее про-z . dev изводной по координате z e' (z) = . Для этого х      d z воспользуемся формулой интегрирования по частям, считая, что ex (z = — L) = ex (z = L) = 0:

LL

J e x ( z ) e^{i 7} z dz = — J e x ( z ) e^{i 7} z dz .

— L               ⁷ — L

Тогда окончательно имеем:

A (y) =

i

72^7 sin ra

L

J e x ( z ) e ⁷ z dz .

— L

. I .           n r             I — i _Yn z

A sin r_oa +-- cos r_Qa e ⁰ +

0 1      0     к ц      0 j

+да /                        x

+ 1 f A (,)I sin ra + n r cos ra I e- ‘ * z d 7 = 0.

V 2 п       l к ц J

—да

Введем обозначения при у = 0, z е [— L ,

[ E x , z е [ — L , L ], e x = E x , e x = I

1 0, z Й [ — L , L ],

Подставим выражение (13) для A ( 7 ) в уравнение (10) и произведем элементарные преобразования. Тогда его можно записать следующим образом:

L

J e x ( ^z ' ) T ( ^z '- ^z ) ^dz ' ⁺ A 0 ^a 0 ^e

—L где

—

-^{i 7} 0 ^z = 0,

и перепишем соотношение (10) в виде ex + ex 0 =

. П r а 0 = sin r 0 a + -—cos r j a , к ц

+х I-

T ^{( z} '^z ) = 27

. П r

1 + ctg ra к ц

- ei y ⁽ z '- z )

+да

A ( 7 ) sin rae

^ ^{7 z}d 7 + A 0 sin r o ae ^{i 7} 0 z

—да

Нетрудно показать, что:

Y

d 7 .

.

—да

Умножим обе части равенства (11) на e^{i 7 z} и проинтегрируем по переменной z от — L до + L ; в результате можно записать следующее выражение:

П r ra П / \ hm —ctg — = yysgn(7), - ^ 1-Ц 7 J к ц ^x

7^ 0 [ к ц

где

L

L

к ц

J e x ( ^z ) e ⁷ z ^dz + J e x 0 ( ^z ) e ⁷ z d^z =

—

— L

L

— L

+да

= 2— [ A ( 7 ) sin rad 7 eⁱ ( ^{7 7} ) z dz + V 2n

—L               —да

Прибавляя и отнимая в квадратных скобках формулы для ядра T ( z , z ') (14) выражение ^П sgn ( 7 ) , к ц     ^{х 7}

произведя перегруппировку и воспользовавшись известным соотношением:

+да

J sgn ( y ) e ^{y (} z z ) d у — z ’- z ,

-да из (14) окончательно получим следующее интегральное уравнение:

-ex ⁽ z ) dz = — f dz'e' (z ')x                 (15)

n k ц ^J z '- z 2 n ^{J x (} )

- L                - L x Ja(y) e y(z'-z) d y + A oao e - 1 Yo z,

-да

-П e' к Ц ^x

⁽ t ) =^-

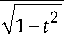
— J e x ( t ) s ( t', t ) dt +

2 _{- 1}

^{+ A} о ^a o ⁿ I ( Y o t ) + D o - .

где введены обозначения

I ( r . t L: 2 ^j

- 1

^—52 e - i ^{Y L v} d v, ^(v- t )

где

a ( y ) —

— +

. y

■^a ( y ) ] . a ( y ) —

r ctg ra        , .

—--sgn ^{( y )} .

Упростим уравнение (16) путем введения новых

переменных z — Lt. z' — Lt\

В этих переменных интегральное уравнение (15)

принимает вид

П 1 e x ⁽ t ' ) ^dt ' k ц J t' - t

= 2" J ^dt 'e x ( t ')^x

- 1

+да x J a (у) e YL(t t)dY + Aoaone 1YoLt.

-да

Ядро интегрального уравнения (16) является сингулярным с особенностью типа Коши. Для его решения воспользуемся формулой обращения интеграла Коши [3]:

1 J • w- < «

- 1

+да

S ( t',t ) = J a ( r ) I ( y . t ) e^{1 Y} Lt d Y .

-да

Функция I ( y o. t ) получается заменой в выражении для I ( у . t ) переменной y на Y o •

В дальнейшем нам потребуется следующее разложение показательной функции [4]:

,i r t_ _?y- ( ¹ ) n J, ( у ) T n ( t ) e 2                          .

n z o    ^{1 +5} n o

где T n ( t ) - полиномы Чебышева первого рода, J n ( a ) - функции Бесселя первого рода.

Полиномы Чебышева 1-го рода связаны с полиномами Чебышева 2-го рода U n ( t ) следующими соотношениями для n >  1 [4]:

T n ( t ) — 1 [ U n ( t ) - U n - 2 ( t ) ] .                          ⁽²¹⁾

U o = T o = 1

U ( t )

T 1 ( t ) = t . T 1 ( t ) =         .

С учетом формул (20) перепишем разложение (21) в удобном для нас виде:

• ^,( t ) =

n 1 - t ²

j ^ f ⁽ t • > dt • t '- t

- 1

a ₀

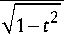
да eYt — Z(i)n [Jn (у)- Jn+2 (y)]Un (t).               (22)

n — o

где a ₀ – неизвестная постоянная, определяемая из дополнительных условий. Считая функцией f ( t ) правую часть уравнения (16), нетрудно записать:

£^{ex (} t ^)—-^

x

1 /     2 f     1             +да

J Л IT J e x ( t ' ) dt 'H t ) • ^Y L ¹ ' d Y +

- 1            I - 1             -да

С учетом того, что

² J k + 1 — J k - J k + 2

бесконечный ряд (22) можно записать в более простом виде [5]:

да eiYt — 2£(1)nJn+1 (Y)Un (t).                          (23)

n — o

Так как

+ A o « о n • ^{1 Y o L v} - d v +

U n ( - 1 ) — ( - ¹ ) X ( t ) .

то

D ₀

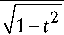
где D ₀ – некоторая неизвестная постоянная.

Преобразуем уравнение (18) к более простому виду:

да e - iY t — 2 E(1) nJn+1( Y )Un (-1)—                     (24)

n—o да

— ² E ( - ¹ ) n J n + 1 ( Y ) U n ( t ) .

n — o

Используя равенство (23) и интегральные представления для полиномов Чебышева [6]:

i /1-"2

U n - 1 ( y ) dy = -n T n ( x ) ,                     ⁽²⁵⁾

y — x - 1

нетрудно получить следующее выражение для I ( y , t ) ^:

to

I ( Y , t ) = - ² Z ( - i ) n J n + 1 ( Y ^L ) T n + 1 ( t ) .               (26)

n = 0

С учетом выражения (25) интегральное уравнение (19) можно записать в следующем виде:

к Ц e^{x (} t > -                                              ⁽²⁷⁾

1       [ to =т^г k(- i ) n V1 - 1 [ n = 0	У j e x ( t ' ) L n + , ( t • ) dt • + - 1
+ 2 n A o a o J n + 1 ( Y o L )	T n + 1 ( t ) + D 0 j -

где a_n – неизвестные постоянные, подлежащие определению.

Получим решение уравнения (30) при учете в разложении (31) для первых трех слагаемых:

e x ( t ) = -p^ ( a 0 T 0 ( t ) + a ₁ T ₁( t ) + a ₂ T ₂( t )).           (32)

71 - 1 ²

С учетом первых трех слагаемых в сумме в интегральном уравнении оно принимает более простой вид:

к Ц ^{ex (} t >=X-

iL j e'_x ( t ' ) 7 1 - 1 ^,2 U 0 ( t ' ) dt '+ (33)

- 1

iL r

+ — f e_x ( t ) M ₁( t ) dt + 2 n A 0 a ₀ J ₁ ( y ₀ L ) T ₁( t ) +

2 1

+

iL e X ( t ') 71 - 1 ^,2 U ( t ')dt ' + L e X ( t ') M ₂ ( t ') dt ' + 2 x 1 2 x 2

- 1                             - 1

Воспользовавшись известным выражением для интеграла [4]:

+ 2nAoaoJ2(YoL) T2(t) + Do’, n1-^ eixt'dx = 2i( 1 (-i)n+171 -t'2U (t'),(28)

x               (n +1)

-to

Откуда можно получить:

+to , ,                                             ___________

WLJeit'УLd(YL) = _2_(i)n 1 -1'2U (t').(29)

YL                (n +1)

-to

Запишем уравнение (27) в более удобном для нас виде:

n e <( t ) = k Ц

71 - 1 ²

) ^to

£(-i) n n=0

L( i ) ^{n + 1} n + 1

■ j e X ( t ' ) Vi — 1 2 U n ( t ' ) dt ' +

- 1

+ у j e x ( t 'NN n + 1 < f) dt ' +

- 1

+ 2nA0a0Jn+1 (y0L) Tn+1 (t) + D0’, где

+to

^N n + 1 ( t ^ ^ Y) J n + 1 ( Y L ) e i ^{Y Lt}' d Y . k ц

-to

Будем искать решение интегрального уравнения (30) в виде разложения по полиномам Чебышева:

N eX( t ) = ^= £ anTn(t).

N 1 - t n = 0

где to

Mn+1 = ТЛ £ (i)mUm(t') j Л(YL)Jn+1(YL)Jm(YL)dY k ц m=0

( n = o, 1).

В дальнейшем нам потребуются следующие равенства:

j U0 (t)To (t)d.t = 2,(34)

- 1

j U 0 ( t ) T ₁( t)dt = j U ₁( t ) T _o ( t)dt = j U ₁( t ) T ₁( t ) dt = 0,

• -1                -1

U _o ( t ) T ₂ ( t )dtt = - ² ,     U ₁( t ) T ₁( t )d.t = ⁴ ,

• 1    Tm(t) Mn+1( t) dt n

  --,   X-t2       (1   m0) кЦ■

■ j ^ЛМ J n + 1 ( y ^L ) I m ( r ^L ) d Y .

-to

Учитывая, что на границах ступеньки при z = = ± Le_x ( z ) = 0, запишем следующее граничное условие:

j e'_x ( t ) dt = 0.                                                (35)

- 1

Подставим решение (33) в граничное условие (35):

^а 0 Г

— 1

dt '

, + a 1 1 — t ^,2

1 Т 1 ( t ' )dt'

— 1

I -----у ⁺ a 2 1 — t '²

1                  .

г Т ( t ') dt ‘ = 0.

— 1

1 — t ' ²

Так как второй и третий интегралы в равенстве (36) равны нулю, то отсюда следует, что а ₀ = 0, поэтому из соотношения (33) нетрудно записать следующую систему алгебраических уравнений относительно а 1 и а ₂:

где

r ctg ra

A ( y ) = —Y-- ^sgn Y .

Запишем множитель форме:

a(y)=y

r cos ra —

A(y)

|y| sin ra

sin ra

.

в несколько другой

П     L п           2   пп

(1 + V K11) a 1 + iL(4 +    K12)а 2 = к Ц     2            3 2к Ц

= 2 п A ₀ а ₀ J 1 ( y ₀ L ) ,

• 2    пп        П     L п

^— i^{L (}- +     K 21 ) a 1 + — ⁽1 + —K 22 ) a 2 =

• 3    2 к Ц          к Ц      2

= 2пA0а0J2 (yoL), где

+да

K ij = J ^A ( y ) J i + 1 ( y ^l ) J j ( y ^l ) d Y .

—да

Полюса подынтегрального выражения опреде ляются нулями знаменателя множителя А (y) : п m    ;— rm = —, m = 1,да.

В этих особых точках

Y m

= ± к к²

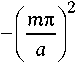
Для больших m ( m ^ да ) можно положить, что

Y m

. m п

» i— .

a

Заметим, что при выводе системы (37) мы воспользовались свойством ортогональности системы функций { т у ( t ) } на отрезке [- 1,1 ] . Используя метод Краммера, выражения для коэффициентов a ₁ и a ₂ имеют следующий вид:

Если ввести обозначение

f = ^{1 Y}

rcos ra — y sinra sin ra

J i + 1 ( y ^l ) J j ( y ^l ) ,

I( n Lп а1 = Т2пA 0 а0 11    (1 + ""^"K22) J 1( Y0 L)

Л 11 к Ц 2

—

то по теореме о вычетах имеем:

K ij = — 2 п i 1 Re sf + ^ Re sf > , | Y= ⁰ ±Y m Y m

^^^^^^в

Re sf = ^{к cos ka} J ^{( o )} J ^{( o )} = ^к ctg ^ka 5 5

_Y = ₀ sin ka j                   ¹

m i'Y m j '* m e sf =---------2--------

Y _m         —Y _m a

+ 4 (1⁺V K 11 ) J 2 ( Y o L )И, к Ц       2                 у I

—

1 a

r _m

Y m

J-h LM h b). i⁴ m j ^Y m

где

А "

( ^к ц)

L п

2 ^{K 11}

— L ² ( ² + Я '²

( 3 2 к Ц ¹²

L ^п К 2 ^{K 22}

—

.

3. Вычисление вспомогательных интегралов K _ij с помощью теории вычетов

Вычислим интегралы K ij ( ij = 1,2), входящие в формулы (37) для нахождения коэффициентов a ₁ и a 2 ^:

+да

K ij = J a ( y ) J i + 1 ( y L ) J j ( y L ) d Y ,                     (39)

—да

Выше мы воспользовались следующими формулами [4]:

Res = M, (sinra)' = -01^0^1^.(40)

g'(a)

Тогда, учитывая, что rm =^m, формулу для на хождения Kij можно переписать в виде

Kij =—2 i п| к ctg ka 5 i o5 j 0 —

2 да ( 2

-;yZ m^ Ji(ymL)J,(ymL))= a m=1 v Y m 7

= 2 п 1 — ik ctg ka 5 i о 5 j о

+ i ^" -¹ J i ⁽Y 1 ^l ) ^J j ⁽ Y i ^{l ) +} a Y 1

ю

• 1    I -^Л          I I I

+ — 7 J- I i—Lm I J- I i—Lm 1^ .

aⁱa^ja m =2   ^{4 у х у}

Так как в нашем случае i , j ^ 0 (для K ij в формулах (38) i , j = 1,2), то первый член в равенстве (41) равен нулю. Ограничиваясь в выражении (41) вторым членом, в первом приближении интегралы K ij можно вычислять по формулам ( i , j = 1,2):

2 i п ³ _ ,

K ij     2 3 ^J i ^{( Y}1 L ) J j ^{( Y}1 L ^).

Yi a

• 4.    Дифракция основной волны прямоугольного волновода на отрезке активной полупроводниковой пленки с отрицательной дифференциальной проводимостью, расположенной на узкой стенке

Из выражения (13) с учетом соотношения (32) для функции e x ( t ) найдем коэффициент A ( y ) :

1 iL

A ^(y)    FT sinra^X

л) 2 пY ^{sin ra}

Интеграл в (45) будем вычислять по формуле вычетов. Используя соотношения (40) и равенство:

‘      2 cos ra

( sin ra y ) =-Y a ------, а также тот факт, что в волноводе распространяется только основная мода, то есть

Y 1 =

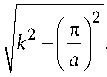
п ^r 1 = ”, a

получаем выражение для составляющей электрического поля в прямоугольном волноводе с отрезком полупроводниковой пленки:

„      . . L п ² |.

Ex = A 0 ⁺ "ЛПТ J ^ia 1 ^J 1 ⁽ Y 1 ^L ) ⁺

Y 1 a I

I 2 J_T (Y! L )

+ a ¹¹

2 I  Y 1 ^l

-

2 J 2 ( Y 1 L ) - J 0 ( Y 1 L ) I >x

x sin r 1 ( a - y ) e i ^{Y z} .

Так как по определению коэффициент прохождения основной волны в прямоугольном волноводе определяется следующим образом:

I 1 xj j 1 - 1

a 1 T 1 ( t ) e ^Y Lt

1 - t ²

1 a₂T ₂ ( t )e i ^{Y Lt} dt +     ² 2

- , Л- t ²

dt

.

Учитывая, что T 1 ( t ) = t , а T ( t ) = 2 t ² - 1, вычислим интегралы в формуле (43):

1 T 1 ( t ) e i ^{Y Lt}

- 1

1 - t ²

T ₂ ( t ) e i ^{Y Lt}

dt = i п J 1 ( y L ),

- 1

1 - t ²

I Ji (YL)            I dt = 2п J--J2 (YL) ^ - пJ0 (YL).

I Y ^L               I

Подставляя значения вычисленных выше интегралов в соотношение (43), получим, что

A ( y ) =

1     i п L

;=-----X

2 п Y sin ra

T = lim

E x ⁽ Y 1 , z )

sin r 1 ( a - y ) e i ^{Y 1} z

то окончательно для него получаем простую формулу

„ .   L п ² I.       _

^T = ^{1 +} о 0 J ^ia 1 ^J 1 ^{( Y} 1 ^L ) ⁺

Y 1 a ² |

^{+ a} 2

1 2 J i (Y1 L )                        У

-1-J1- - ² J 2 ⁽Y 1 L ) - J 0 ⁽Y 1 ^L ) .

I ^Y 1 ^L                      J

I                  I 2 J_T ( y L )

x J iaJ ( y L ) + a ₂ I —---

I ¹¹       2 1   Y ^L

-

2 J 2 ( y L ) - J ₀ ( y L ) I > .

С учетом выражения (44) для A ( y ) , электриче-

Для вычисления модуля коэффициента прохождения T(a), в дальнейшем обозначаемого T(a)|, где a = Y1 L, и фазы коэффициента прохождения argT(a) необходимо вычислить коэффициенты a1 и a2. Вспомним, что к 5

П =----------- ,

• 2 ,

• 1-    — г²

¹   4 ^r no

ское поле в волноводе образом:

E x = A ₀ sin( r 1 ( a - y )) e ^- i ^{Y 1 z}

определяется следующим

+x

1I x            J ia 1J 1( yL) + a 2

Y sin ra I

-^         ¹

iL + X

I 2

■ ( Y L

22  2

где r no = к ^e n -Y 1 , а комплексная проницаемость пленки Б п = ^е- i 4 по / го . Тогда для коэффициента П получим следующее выражение:

П = П 1 ^- i П ₂,                                            ⁽⁴⁷⁾

-

П 1 =

к 5 с

-

У

2 J ₂ ( Y L ) - J _o( Y L ) ^ sin r ( a - y)e i ^{Y z}d y .

JJ

I               Л2 У

„2 I Z,2s2 ^G I с -1 п к 5 — I

I го J

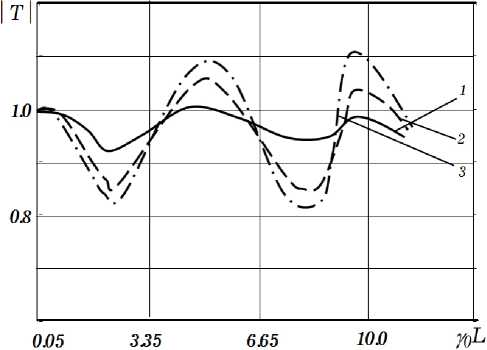
Рис. 2. Зависимость модуля коэффициента прохождения T от длины полупроводниковой пленки Y i L : ^{е =} 10; ° / ю = 1;

f = 40 ГГц, 1 - к 8 = 0,01; 2 - к 8 = 0,1; 3 - к 8 = 0,3

Fig. 2. Dependence of the modulus of the transmission coefficient

T on the length of the semiconductor film y 1 L : 6 = 10; ст / ю = 1; f = 40 GHz, 1 - к 8 = 0,01; 2 - к 8 = 0,1; 3 - к 8 = 0,3

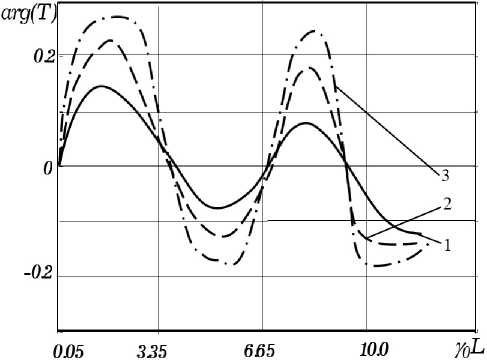
Рис. 3. Зависимость аргумента коэффициента прохождения T от длины полупроводниковой пленки Y 1 L : е = 10; ст / ш = 1;

f = 40 ГГц, 1 - к 8 = 0,01; 2 - к 8 = 0,1; 3 - к 8 = 0,3

Fig. 3. Dependence of the transmission coefficient argument T on the length of the semiconductor film y 1 L : s = 10; ст / ю = 1;

f = 40 GHz, 1 - к 8 = 0,01; 2 - к 8 = 0,1; 3 - к 8 = 0,3

п ( к 8 ) ³ ° ю

П 2 =

Из анализа кривых, изображенных на рис. 2 и 3 следует, что функции | т | и arg( T ) имеют резонансный характер, причем минимальному T соответствует максимальное значение arg( T ). Можно сделать вывод, что при малых значениях к 8 ( к 8 = 0,01) | т | и arg( T ) изменяются мало и кривая 1 (соответствующая случаю к 8 = 0,01) близка к штриховой линии (случай ° = 0). При увеличении к 8 увеличиваются пределы изменения | т | и arg( T ). Из рисунка следует, что существуют такие интервалы у 1 L (при к 8> 0,1), где коэффициент

T становится больше 1, что соответствует случаю усиления электромагнитной волны в активной полупроводниковой пленке с отрицательной дифференциальной проводимостью.