Promising quantum engineering of optical even/odd Schrodinger cat states

It is a well-known fact that the generation of two-mode entangled light state can be realized by interference of single-mode non-classical states at the beam splitter [1]. The canonical example of the interference is known to be Hong-Ou-Mandel (HOM) effect [2], which is a two-photon interference effect with two single photons emerging together at one of the outputs of the balanced beam splitter with half chance of success. The process of mixing of the non-classical states serves as a critical element in such an application as quantum state engineering using technique of photon subtraction [3–6], photon addition [7], and photon catalysis [8, 9]. The interference of two non-classical states at a beam splitter can become resource for a conditional quantum engineering of desired optical states.

In optics, implementation of superposition of coherent states | + β 〉 and | - β 〉 with complex amplitudes ±β is of considerable interest. Realization of the non-classical Schr ӧ dinger cat states (SCSs) is expected to resolve the puzzle, at what degree of macroscopicity, if it exists, the object goes on to be quantum [10]? The squared absolute value of amplitude of the component coherent state | β |² , which is approximately equal to its mean photon number, can be to some extent treated as a qualitative measure of SCS macroscopicity. It must be at least much larger than the quantum uncertainty 1/ 'J 2 of the position observable in the coherent state in order to recognize an optical SCS macroscopic object [11]. In addition to their fundamental importance, the SCSs have high application potentials in teleportation [12– 15], quantum metrology [16], quantum computation [17, 18]. Here we propose a new theory for the generation of a family of CV states of definite parity whose practical potential is as yet unknown. The generation is based on the use of a photon number resolving detector, which implements the new measurement-induced CV states of definite parity. Nevertheless, we consider one important practical application of the family under study, namely the possibility of using the CV states of definite parity in the quantum

Физика engineering of even/odd SCSs. The approach uses irreducible number of optical elements and can be implemented in practice.

For quantum engineering of optical even/odd SCSs, we consider the optical design in Fig. 1 con- taining irreducible number of optical elements. It consists of a lossless beam splitter BS =

t

r

- r

t

with real transmittance t > 0 and reflectance r > 0 coefficients satisfying the physical condition t2 + r2 = 1. The beam splitter (BS) is considered to be no longer necessarily balanced and its parameter can be arbitrary. In Fig. 1, single-mode squeezed vacuum state in first mode with amplitudes

^,                                   (2 n )!.

I SMSV ) =       Z b 2 n |2 n ) = -j=T Z !=; ^{( L} |2 n ) ,

V coshs _n = 0           V coshs _n = 0 J( 2 n )! n !

^b 2 n

У  ( ² n ) !

V(N! ^{n !}

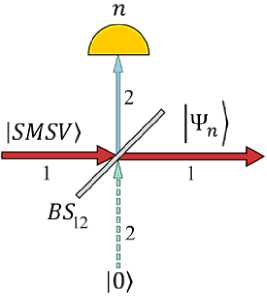
Fig. 1. An optical scheme used to generate CV states of definite parity either even or odd. It consists of the beam splitter with arbitrary BS parameter t through which the original SMSV with squeezing amplitude s passes. Second measurement mode is used to measure number of photons and implement new measurement induced CV states | Y„) , where either n = 2 m

or n = 2 m + 1

enters to the beam splitter. Here, amount s >  0 is the squeezing amplitude of the SMSV state the parameter 0 <  y = tanhs /2 <  0,5 of the SMSV is introduced. The absence of input SMSV (vacuum) is determined by the value y = 0, while the value of y = 0,5 corresponds to the nonphysical case of an infinitely large squeezing amplitude s ^ да of the original SMSV that goes behind physical consideration. No other state (vacuum) is applied to the second input BS. As can be seen from Fig. 1, part of the initial photons is diverted to the second mode of the BS, where they are detected PNR detector. In the case of detecting a photon state in the second auxiliary mode with the PNR detector, the original SMSV can be transformed into a new CV state, which we are going to call 2 m /2 m + 1-heralded CV state by the number of extracted photons. Success in the development of photon-resolving detection [19] allows one to hope for the successful implementation of scheme in practice.

The analytical derivation of the 2 m /2 m + 1 -heralded states starts with transformations of the creation operators

imposed by the beam splitter: a + ^ ta + - ra + , a 2 ^ ra + + ta + that, due to linearity of the BS operator,

realize the following unitary transformation over input SMSV state

да

BS 12 ( I SMSV ) 1 | 0 ) 2 ) = -—= Z C I ^ n ) 1 1 n ) 2 , V coshs _n = 0

where the amplitudes C_n are determined as

C n

1 - t t ²

n

² ^ 2

y ^ ² I   V Z (2 m ) ( У 1 ), if n = 2 m ,

V n ! |^ Z ^{(2 m + 1)}( y 1 ), if n = 2 m + 1,

where, by definition, the following function Z = Z ( y 1 ) = Z ^{( 0 )} = 1/ ^1 - 4 y 1 ²

and its derivative

Z(n) = dnZ / dyn with respect to the parameter y1 = t2tanhs / 2 determined through the experimental parameters (t,s) are introduced. The parameter y1 differs from the parameter y by the value t12 i.e. y1 = t2y . By definition, the parameter y1 can also take values in the range 0 < y1 < 0,5 in the case of

Podoshvedov M.S., Podoshvedov S.A., Alodjants A.P., Kulik S.P.

Promising Quantum Engineering of Optical Even/Odd Schrödinger Cat States

• 5    >  0, where the case y = 0 is realized either in the absence of the SMSV at the input to the BS ( 5 = 0 ) or in the case of reflection of all photons into the second auxiliary mode t = 0, r = 1, while the case of y = 0,5 can be done in the non-physical case 5 ^ w and t = 1. The CV states | *) are given below.

Consider the possibility of using entangled state in Eq. (3) for quantum engineering of new non-classical CV states. The projection of the state in Eq. (3) onto Fock states by the registration of n photons in auxiliary second mode leads to heralded generation of new CV states. So, measurement of an even number of photons n = 2 m in the second auxiliary mode realizes 2 m -heralded CV state

1 ^w    v ⁿ

। * 2 m )=       Z -T=

Y |2 n ) ,

while if the observer registers an odd number of photons n = 2m +1, then 2m +1 -heralded CV state becomes w     Vn y1  У   y1

„ ( 2 m + 1 ) ^z

12 n + 1 ) .

Thus, the subtraction of either even n = 2 m or odd n = 2 m + 1 number of photons from original SMSV in an indistinguishable manner with loss of all information from which Fock states of the original superposition the photons are subtracted generates the heralded CV states of definite parity in Eqs. (5), (6). The output states have a well-defined parity either even (superposition involves only even number states) or odd (the measurement induced state consists exclusively of odd number states) in dependency on the parity of the measurement outcomes. It is interesting to note the state in Eq. (5) becomes SMSV in Eqs. (1), (2) in the case of m = 0 and y 1 = y . It is worth noting the family of the CV states in Eqs. (5), (6) depends on one parameter y ₁ as well as the initial SMSV state from which they stem. For this reason, they can also be called SMSV-like states whose non-classical properties may be of interest for optical quantum metrology. The success probabilities to realize the 2 m /2 m + 1-heralded states follow from definition of the amplitudes of the entangled state in Eq. (4)

, ₌ ¹

2 m        _ coshs

, ₌ ¹

2 m+1         _ coshs

1 - t^г t^г

x 2 m

У ² m ₇mm )

( 2 m ) !        ,

~ \ 2 m +1

1 - 1 ²

t ²     ,

2 m + 1

( 2 m + 1 ) !

( 2 ( 2 m + 1 )

with the normalization condition Z ”_ _QP_n = 1 which is directly checked.

Now, we are interested in the possibility of approximating even/odd SCSs, being the superposition of coherent states with real amplitude в > 0 equal in absolute value but opposite in sign (| SCS±) = N± (в)(| в)± I —в))), by the heralded CV states of definite parity in Eqs. (5), (6). Indeed, such a task makes sense since the 2m /2m +1-heralded CV states of definite parity may have photon distributions similar to even/odd SCSs ones о 2 n

| SCS + ) = 2 N + ( в )ехр( - в ^)V ,- £ = 12 n ) , ^{n 0} V<2 n )!

о 2 n + 1

| SCS - ) = 2 N - ( в )ехр( - в y>V ”_₀- в =— 12 n + 1 ) , V ⁽2 n + ^1)!

where N ± = [2(1 ± exp( - 2 в ))]

1/ 2 are the corresponding normalization factors. Difference between the

states in Eqs. (5), (6) and (9), (10) is that the amplitude в is raised to a power of 2 n ( в ² n ) in Eq. (9) and 2 n + 1 ( в 2 n ^{+ 1} ) in Eq. (10), unlike the parameter y ₁ to the power of n in Eq. (5), (6). But instead, the CV states of definite parity in Eqs. (5), (6) have an additional factor either ( 2 ( n + m N ) ) !/ ( n + m N ) !

Физика in Eq. (5) or (2(n + mN +1))!/(n + mN +1)! in Eq. (6) associated with the number of extracted photons from SMSV which may compensate for the difference between pn, вn+1 and yn •

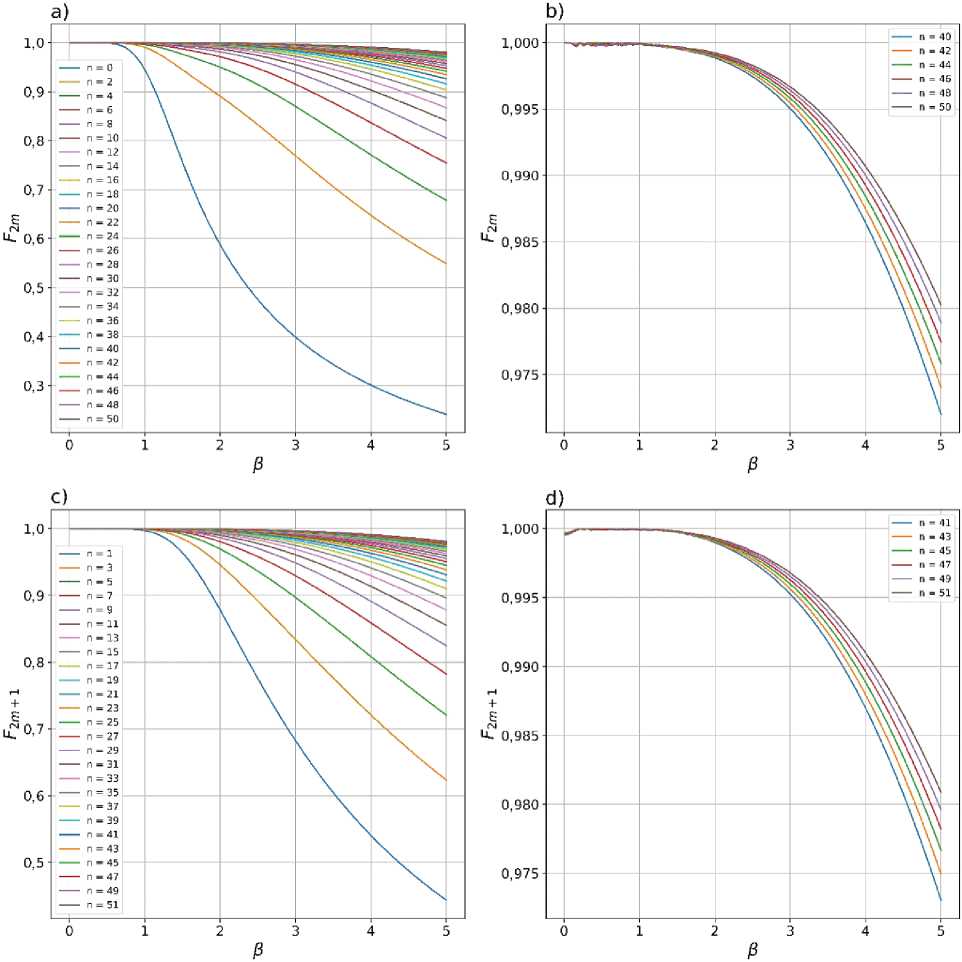
Fig. 2. Dependence of the even (a), (b) Fm and odd (c), (d) F2m+i fidelities between 2m,2m +1 -heralded CV states of definite parity and even/odd SCSs on the SCS’s amplitude p . The more photons n are subtracted in auxiliary modes, the higher fidelities F of the generated states can be observed. Dependences of the fidelities of higher-order CV states with n from 40 up to 51 depending on p are separately shown in subfigures (b) и (d). The dependences on subfigures (b) и (d) allow for one to observe generation of even/odd SCSs with an amplitude greater than 4 with fidelity exceeding 0,99

To assess how well the 2 m /2 m + 1 -heralded CV states can well approximate even/odd SCSs, we use the fidelity either F_2m = | { SCS ₊ | T _{2 m} ) |² or F_{2m + 1} = | { SCS - | ^ _{2 m + 1} ) |² , which is a measure of the proximity of two pure states. The value F _{2 m} = F _{2 m + 1} = 1 corresponds to the complete identity of two pure states. In Fig. 2, we show the dependence of the fidelities F (Figs. 2, a , b ) and F (Figs. 2, c , d) on the SCS’s amplitude p . The dependences are obtained by searching for the global maximum of the fidelities by parameter y 1 at some constant value p . As can be seen from the plots, the more photons are extracted from the original SMSV, the greater the fidelity of the generated SMSV-like states

Podoshvedov M.S., Podoshvedov S.A., Promising Quantum Engineering Alodjants A.P., Kulik S.P. of Optical Even/Odd Schrödinger Cat States with the even/odd SCSs with greater amplitude. We limited ourselves to 51 subtracted photons, but in general, an increase in the number of extracted photons can only lead to an increase in the fidelity between the generated states and even/odd SCSs of larger amplitude в . So, if for the measure of the required fidelity one chooses the value F2m = F2m+1 > 0,99, then the extreme values of the SCSs amplitudes at which such fidelity is still observed are в = 4,04 (in the case of subtraction of 50 photons in Fig. 2(b)) and в = 4,093 (in the case of subtraction of 51 photons in Fig. 2, d). The plots in figure 3 show the dependency of y and y (for convenience, in Fig. 3 when designating the vertical axis, we do not use the subscript 1 for the parameter y ) which provide the maximum fidelities F and F2m+i in Fig. 2 on в • It is interesting that the more photons are subtracted from the original SMSC, the smaller the value of the parameter y can acquire. For example, subtraction of large number of photons (say 50 or 51) from input SMSV leaves the parameter yx in the range yT < 0,2 what could have prac- tical potential when choosing parameter values s and t .

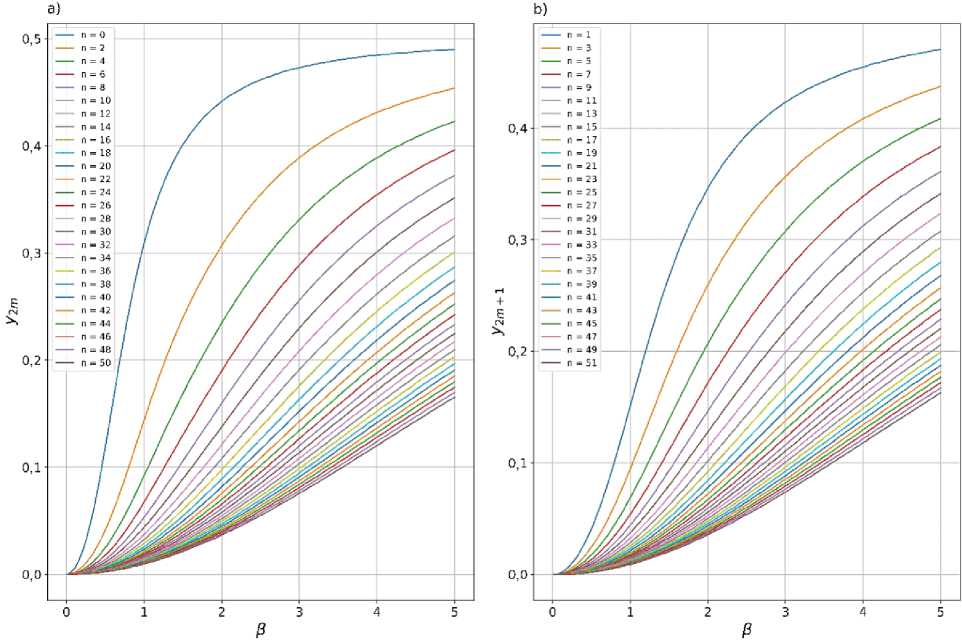
Fig. 3. 2m,2m +1 -heralded states in Eqs. (4,5) depend solely on one parameter 0 < yk < 0,5 . The plots demonstrate the dependencies of the parameter yk that provide the fidelities in Fig. 2 on the SCS amplitude в ■ The larger the number n of the extracted photons, the smaller the value of the parameter y , moreover accompanied by an increase in the fidelity of the conditional states

As for generation rate of the even/odd SCSs, which is proportional to the success probability in Eqs. (9), (10), it already depends on two parameters y and t , in contrast to the fidelity. As an example, we present plots of the success probabilities in Eqs. (7), (8) versus в starting with n = 6 up to n = 16 for even and n = 7 up to n = 17 for odd SCSs. In general, increasing the number of extracted photons can only decrease the success probability in realizing the required CV states.

In conclusion, we have introduced a family of CV states of a certain parity which in their statistical properties may be similar to original SMSV state from which the CV states of definite parity stem. The key point in their implementation is the extraction of an arbitrary number of photons in an indistinguishable manner by means of PNR detection while preserving the superposition properties of the new CV

Физика states. The imperfection of optical elements, e.g. non-ideal quantum efficiency of the PNR detector, can impose certain restrictions on the generated states, which is the subject of further study. As an example of the application of the CV states of a certain parity, we have considered the possibility of creating a generator of even/odd SCSs states. For the first time, we reported the possibility of realizing even/odd SCSs of amplitude a little over 4 with fidelity > 0,99 on a given type of optical design in Fig. 1. The optical design used can be upgraded to generate new states more efficiently. For the experimental implementation of the proposed scheme, one can use the technique described in references [20, 21].

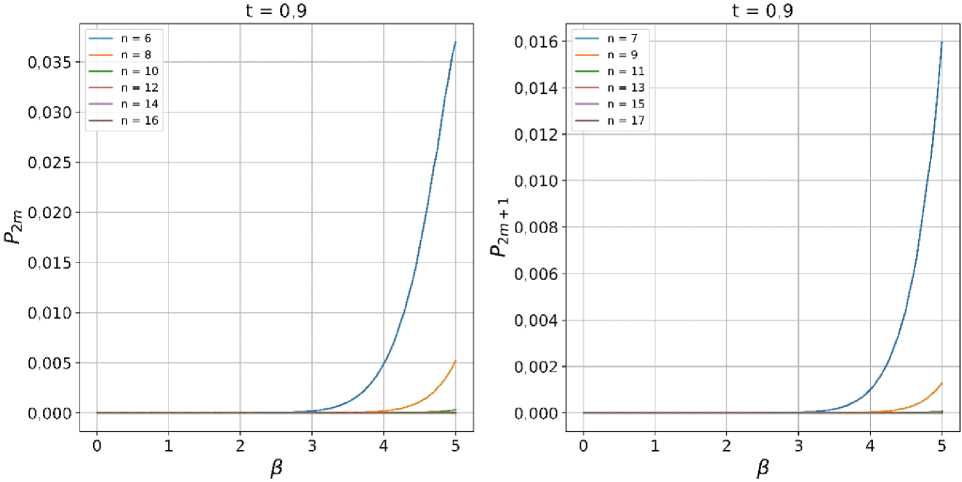
Fig. 4. Dependencies of (a) P 2 m (Eq. (7)) and (b) P_m+\ (Eq. (8)) on the SCS amplitude p for some n = 6 - 17 . In general, the dependences indicate that the extraction of a larger number of photons leads to a decrease in the success probability of generated CV states of definite parity approximating even/odd SCSs with the highest possible fidelity for a given p