Proposed Representation Approach Based on Description Logics Formalism

Published Online May 2016 in MECS DOI: 10.5815/ijisa.2016.05.01

The knowledge representation is a very important aim for artificial intelligence; it can be a beginning for intelligent behavior generation. Lots of representation formalisms are created for this goal. They are constrained by being well structured, usable, simplified, and expressive like the most important constraint.

The description logics formalism is one of the most important representation formalism. This last based on two kinds of relations: the subsumption and the equivalence that define expressions using constructors like union (disjunction), intersection (conjunction), and negation (complement). This formalism provides more detail by the quantification and the restrictions possible by the existential quantifier, the universal quantifier and the numerical restriction. These tools provide a strong and expressive formalism of knowledge representation. And allows to define The minimal language AL as “contains the atomic concepts, the universal concept, the bottom concept, atomic negation, intersection, value restriction and limited existential quantification”.[1].It leads to seeking for best reasoning Algorithms based on these definitions.

Description logics are defined as a family of logicbased knowledge representation language that can be used to represent the terminological knowledge of an application domain in structured way [2] .

To rich more expressivity of knowledge representation DLs languages have seen many augmentations, and developments.

The implementation of DLs systems faces to problematic the effectiveness of reasoning Algorithms and expressivity of representation that means: “DLs systems need booth expressive logics and fast reasoner procedures for deciding subsumption (or equivalently satisfiability) in such logics have discouragingly high worst-case complexities, normally exponential with respect to the problem size”[3] .

In this paper, we present a new representation approach based on description logics, which simplify the implantation of DLs systems using vectorisation of concept definition after an automated investigation of direct subsumption relations. This representation replaces the complex expressions by an attribute that we called Subsumption Hierarchical Attribute SHA .

The reminder of this paper figures like following: a background speaking about motivations and defining briefly the field of study with a brief subsection illustrating related works, the second section is called contribution; where we describe the proposed approach, and the third represent the study of the convergence of reasoning algorithm, finally we discus advantages and weaknesses of the proposed approach.

• II.    M otivations

DLs systems are really presented like a strong representation formalism but it allows some deficulties that can rich in some cases the indecidability problem. Seeking for more expressivity to define models of an existing reality leads to complexe manipulations which descourage the works on reasoning Algorithms implementations.

The smalls augmentation on simple DLs laguage can encrease the complexity of any duduction procedure, that means “even a seemingly simple addition to a very small language can lead to subsumption determination becoming NP-hard.”[4]

Also it is proved that “adding the ability to represent equalities of role compositions makes the complexity of the subsumption problem leap from quadratic to undecidable.”[5]

As result of these remarques thier are three possible responses wich are :

• •    Provide an incomplete implementation of the DL reasoner, in the sense that there are inferences sanctioned by the standard semantics of the constructors that are not performed by the algorithm.

• •    Provide a complete implementation of a specific DL reasoner, acknowledging that in certain circumstances it may take an inordinate amount of time.

• •    Carefully devise a language of limited expressive power for which reasoning is tractable, and then provide a complete implementation for it.[6]

These dificulties are reflecting on implementation. The objectif of performing DLs systems leads to think about conception of representative structure. This lasts must be simple in creation and use, and also powerly expressive.

• III.    D ls S ystems P erforming

In the current generation of DL-KRS, the need for complete algorithms for expressive languages has been the focus of attention. The expressiveness of the DL language required for reasoning on data models and semistructured data has contributed to the identification of the most important extensions for practical applications.[7]

The need of complete reasoning Algorithms, acting on expressive DLs knowledge bases has introduced to lot of optimization techniques. These two properties represent the two majors’ objectives in DL-KRS implementations. The completeness represents the ability to deduce all true facts using the rules on system. Where the expressiveness, represent the power of a representation to characterize knowledge.

Before designing and implementing a DL-based knowledge representation system, the implementers should be clear about the goals that they are trying to meet and against which the performance of the system will ultimately be measured.[3]

For this fact testing and optimizing DL-KRS is relative to the goals of implementation. It is why, it is to be admitted that the primary goal is the utility in the developed application.

But the generic goals in performing DLs system are the efficiency and effectiveness. This first one rises in the use of memory and the time customization, where the second is measured by the ability to explicit implicitly represented knowledge in KB.

This proposed approach has as goal to create a complete efficient reasoning algorithm using vectorial representation derived from the inspection of direct subsumption relationship in DLs knowledge base.

• IV.    S ubsumption R easoning in DL s

Reasoning with DL knowledge bases is a deduction process which extracts not only the facts explicitly asserted in a knowledge base but also their logical consequences as well [8]. This deduction makes explicit the hidden subsumption relationship between two computable concepts using structured reasoning Algorithms, then as consequence the determination of the hierarchy of concepts defined in a TBox.

The advantage of these Algorithms is that by preprocessing concept descriptions and storing them in a normal form [9], subsequent subsumption (subsuming) tests, of which many will be required to maintain the hierarchy concept that can be performed relatively and efficiently [10].

Disadvantages are that the structural comparisons required to deal with more expressive description languages become extremely complex [11]. Although it has a negative effect, it is known that it can achieves more expressivity and completeness for the reasoning Algorithm by transforming the subsumption problem to non-satisfiability problem. “The satisfiability… problem can then be solved using a provably sound and complete algorithm based on the tableaux calculus” [12].

Applying some simple optimization techniques to a tableau algorithm can result in performance, which is comparable with incomplete structural algorithms [13]. The reason of this work is to investigate the impact of a simplified representation on the performance, because this representation can carry the meaning of subsumption and consequently the one of the satisfiability considered as in a finite domain.

It is to be noted that it is very simple to speak about assertions Box because it define for each simple predicate -the concept- in which every individual is occurring and for each binary predicate –roles- every pair of individual who satisfy the role definition.

• V.    R elated W orks

The searchers in the field are working for the DLs systems optimization but we can’t find in literature works on vectorial form derived from the subsumption relationships. This fact makes the novelty presented in this paper.

The efficiency of reasoning algorithms is viewed like a problem of optimization that reduces the complexity of an algorithm and gives the same or better level of performance. In literature, we find some works aiming at the same objectives but touching different aspects as: Nenad Krdžavac and his collaborators, in 2009 declare “The implementations are not based on original definition of the abstract syntax, but they require transformation of the abstract syntax into concrete syntax implementation languages use]. [The use of model-driven engineering principles for the development of a DL reasoner where a definition of a DL abstract syntax is provided by means of metamodels”[14]. We find also the work Hustadt with his groupe in 2007 “developed a novel reasoning algorithm that reduces a SHIQ knowledge base to a disjunctive Datalog program while preserving the set of ground consequences” [15]. And recently, in 2012, the work presented by Cuenca with his collaborators “proposed a theoretical framework and practical techniques for establishing formally provable and Algorithmically variable completeness guarantees for incomplete ontology reasoners” [16].

• VI.    C ontribution

• A.    Subsumption Hierachical Attribute

The SHA represents a vectorial attribute that can carry the subsumption meaning, each component represents a nodes of the tree of subsumption hierarchy.

Every SHA vector gives the path from the root to the node representing the concept, it’s why it is possible to find one concept defined with more than one SHA vector.

It is known that we can reduce every equivalence relation to subsumption: A is equivalent to B if and only if A is subsumed by B and B is subsumed by A (A and B represent concepts). By this way we can construct the dependency graph of subsumption.

D	с	С	(1)
В	с	С	(2)
А	Е	D	(3)

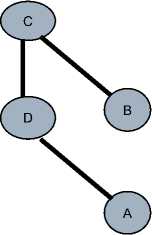
Fig.1. The subsumption hierarchical structure

Then, every node will have a number by sequential codification that begins by “1” for each level. The path from root (more general concept) to the concerned node makes the representative vector using this numbers. See figure 2.

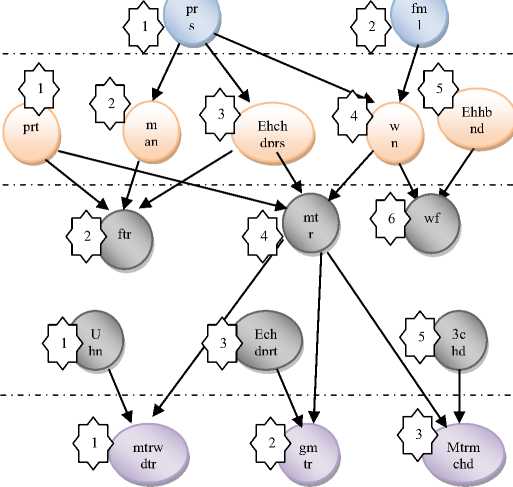
Fig.2. The subsumption hierarchical indexation

This table illustrate names of nodes in figure2

Table 1. Abbreviation for human being knowledge bases

Abbreviation	Concept name
Prs	Person
Fm	Female
Prt	Parent
Man	Man
Ehchdprs	3 haschild. person.
Wn	woman
Ehhbnd	3 hashusband
Ftr	Father
Mtr	Mother
Wf	Wife
Uhwn	Vhaschild. woman
Echdprt	3 haschild. parent
3chd	> 3 haschild
Mtrwdtr	Mother without daughter
Gmtr	Grandmother
Mtrmchd	Mother with many children

• B.    Auomated Geneation Process

The first step of the SHA generation process is the direct subsumption detection which consists in representing the axioms defined by equivalence relation in subsumption based form. This representation is based on implications existing between the two kinds of representation. Like sets treatment each definition using constructors can be reduced to a group of subsumption (inclusion) relation as follows.

C ≡ D ∩ В => (с⊂D) ∧(С⊂В)

C ≡ D U В => (D⊂С) ∧(В⊂С)

С ≡ В => В∩С ≡ Ф

Reducing he complex expressions to simple subsumption expressions needs some iteration based on other rules after the application of this specified below as initial treatments. For reasons of expressiveness, indicators, to represent the infinite and the finite subdomain, are needed. The infinite sub-domain comes from the relations of subsumption between a concept and an expression like

С ⊂ (D U В)                 (7)

which means that there is a part of a set which can be a small part or big part or the whole of the super set. This probable forms cause less expressive representation and make useful the use of the infinity indicators for each sub-domain.

(D ∩ В) ⊂ С => Ǝ А,(D∩В) ∩С≡=>

(А⊂D) ^ (А⊂В) ^ (А⊂С)

(D U В) ⊂ С => (D⊂С) ^ (В⊂С)

С ⊂ (D ∩ В) => (С ⊂ D) (С ⊂ В)

С ⊂ (D U В) => ( С ⊂ D ) V ( с ⊂ в )

V(с⊂ (D∩В))

For the roles level, the role is seen as binary relation between two sets of individuals. The expression R.C corresponds to the individuals in relation with C by R. For example, the sentence “individuals having a female child” is presented ∃ hasChild. Female, and the sentence “individuals all of whose children are female” is presented ∀ hasChild. Females[03]. By the same way the number restriction is represented to integrate cardinalities. (See figure03)

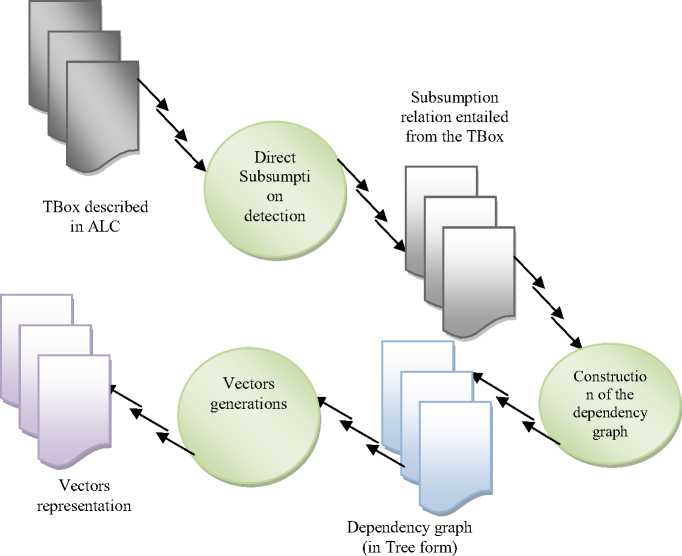
Fig.3. The SHA generation process

This proposed process is completely computable with high effectiveness degree. But it’s to be mentioned that for implementation we use a reduced syntax.

• C.    Automated Process

To accomplish this task, a simplified syntax has been used. The implemented interface analyse the introduced text respecting the polish notation generated by the proposed reduced syntax and generate SHA vectors after inspecting the direct subsumption relation between concepts.

S	→	% OP | C
OP T	→ →	CON(S,S )| Neg (S)| T R.C| EX | UN |<=Number	The terminal	alphabet is
CON → C → R →		| >=Number Conj | Disj	giving like: conjunction, Disjunction,	Conj for Disj   for

Using this rule the application is made to provide an interface for integration and generation of SHA like in following figures.

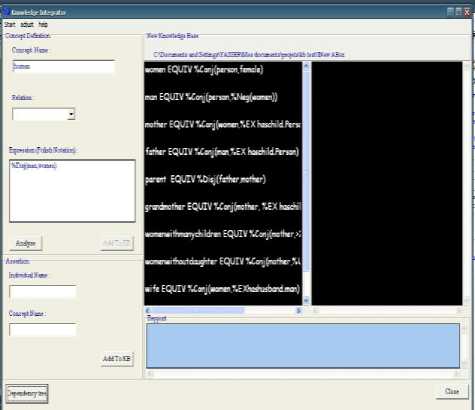
Fig.4. The main frame of the SHA generator soft ware.

After being analyzed and add line by line the resulted text representing a part of the knowledge base is treated to inspect the direct subsumption relation between concepts. This task is necessary to generate SHAs. (see figure 5)

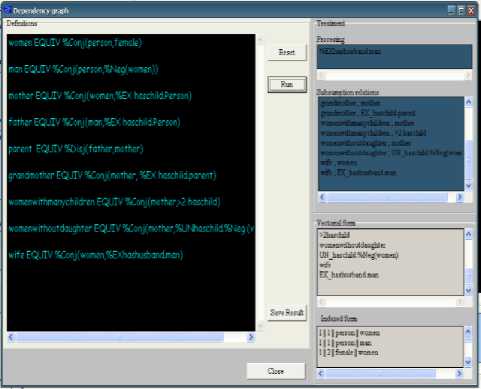
Fig.5. Indexed hierarchy generator

• D.    Rules in Vectorial Form

In this section we present how to adapt the reasoning rules on the new representation structures. Each component in SHA has a signification thing that makes the deduction process based on vectors comparing.

In follows the Tableau ALC rules can be transformed to deal with the vectorial representation with graphical illustrates.

The ∩-rule

If A contains (C 1 ∩ C 2 )(x), but not both C 1 (x) and C 2 (x) then

A '= A U {C.CO^GO}        (12)

P is the constructed by the conjunction between C 1 & C₂ which yields to two vectors (c 1 ,.......,c k ,0, ,0) and

(b 1 ,..........,b k ,0,.......,0) with c k = b k.

Condition

If we find another concept A with vector V of the form (a 1 ,.........., a k ,0,.......,0) where a k = c k = b k

Action

• 1.    Create a node A’ with representative vector of the form (a 1 ,-1,.......,-1, t,0,.......,0) where t-1 is number of

• 2.    Add new vectors to define A , C 1 and C 2 like follows

concepts in level k-1.

A^(ai,-1,.......,-1, t, ak,

Ci^(ai,-1,.......,-1, t, ck,

C2^(a1,-1,.......,-1, t, bk,,0)

And by the way each concept subsumed by A, C 1 or C 2 must have new vector defined by taking the left side of this three vectors.

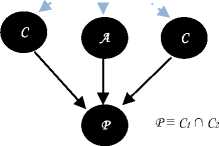
Fig.6. Representation of the rule of conjunction applied to the vectorial form

The U-rule

If A contains (C 1 ∩ C 2 )(x), but neither C 1 (x) nor C 2 (x) then

A '= A U {^(x)} and A"=A U [C₂(;c)}     (13)

Let’s suppose A , C 1 and C 2 concepts represented by

P is the constructed by the disjunction between C 1 & C₂ which yields to two vectors (a 1 ,.......,a k- ,a k ,c k+1 ,......,0) and

(a 1 ,.........,a k-1 ,a k ,b k+1 ,.......,0)      representing C₁ and   C₂

respectively

Condition

If A is represented by a vector in the form (a 1 ,.......,a k-

(a 1 ,.......,a k-1 ,a k ,c k+1 ,......,0) , (a 1 ,.........,a k-1 ,a k ,b k+1 ,.......,0).

Action

• 1.    Create two new nodes A’ and A” with vectors (a 1 ,-1,.......,-1, t,0,.......,0), (a 1 ,-1,.......,-1, t+1,0,.......,0) while

• 2.    Add new vectors to define A , C 1 and C 2 like follows

t-1 is number of concept existing in level k-2.

A *    (a l , ^-1,.......^,-1, t, a k-1,....... ,0) , (ab ^-1,.......^,-1, t+1, a k-

• 1,,0)

P *    (a i ,-1,.......,-1, t, a k-i ,a k ,0,.....,0), (a i ,-1,.......,-1, t+1, a k-

1,ak,0,,0)

C 1 * ( ^a 1 , ^-1,.......^,-1, t, ^{-1, -1,} c k+1,....... ^,0) , ( ^a 1 , ^-1,.......^,-1, t ^+1,

• -1,-1, c k+1 ,.......,0) , (a 1 ,-1,.......,-1, t, a k-1 ,a k , c k+1, 0, ,0) , (a 1 ,-

• 1,.......,-1, t, ak-1,ak, ck+1, 0,,0)

C2 * (a1,-1,.......,-1, t+1,-1, -1, bk+1,.......,0) , (a1,-1, t+1, -1, -1, bk+1,.......,0) , (a1,-1,.......,-1, t+1, ak-1,ak, ck+1, bk+1,

0, ,0) , (a 1 ,-1,.......,-1, t, a k-1 ,a k , b k+1 , 0, ,0)

By this same method we define new vectors for every subsumed concepts derived from this concepts

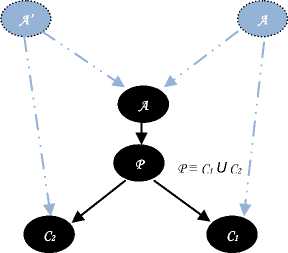
Fig.7. Representation of the rule of disjunction applied to the vectorial form

The Ǝ -rule

If A contains ( Ǝ R.C)(x) but there is no individual name z such that C(z) and R(x,z) are in A then

А ’=А U (C(y),R(x,y)}         (14)

where y is an individual name not occurring in A

In this rule the condition specified the individuals z such as R(x,z) occurring in C but not in A which contains the concept defined by ( Ǝ R.C)(x) . This leads to a vectorial definition like in follows.

Note that when the condition is verified the actions need to create some new nodes to represent the sub concepts of C and A.

Lets define A₁ ={a, A(a) ˄ R(x,a) with C(x)} and A₂={y, C(y) ˄ R(x,y) with c(x) ˄ ̚A(y)} then we imagine when A and C are represented by (a 1 ,.......,a k ,0,......,) and

Condition

If there is no individual z occurring in C and not in A having relation with x such as R(x,z) , which means an individual occurring in A 2 .

Action

Create A’ (a0, -1,.......,-1,t,0,.....0) where (t-1) is the number of concept in level (k-1) and A’≡ A U A2 , add new vectors in definitions of A, A2 and there sub concepts are like in precedent.

A ^   (a 1 ,-1,.......,-1, t, a k , 0,.......,0)

A 2 ^    (a 1 , -1,......., -1, t, a k , -1,-1, a k , 0,.....,0)

With this same method we define new vectors for every concept subsumed by all concepts having new representatives vectors.

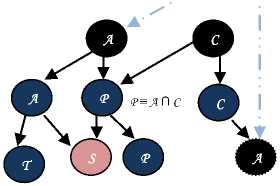
S ≡ P ∩ A 1

Fig.8. Representation of the rule of existential quantification applied to the vectorial form

The V rule

If A contains (V R.CXx) and R(x,y) , but it does not contains C(y) then

А' = А U {C(y)}

We suppose that  A(a1,........,ak ,  0,  ....0) andC(a a1’,......,ak’,00)

The concept A 1 ={x, A(x) ˄ R(x,y) with C(y)}

Condition

If A contains A 1 and not C(y)

Action

Create A’(a1, -1, ........, t, 0, ....., 0) while (t-1) is number of concept in level (k-1)

Add vectors for A and C and all of their subsumed concepts

A ^   (a 1 ,-1,.......,-1, t, a k , 0,.......,0)

C *    (a 1 , -1,......., -1, t, a’ k, , 0,.....,0)

n!

Ti to= -77-----7 .Px .(1 — Р)

x! (n-x)!

n-x

!      (nP)    (1-P)

(n- %)!n^x .   %!     . (1 -P)^x

We accept these three additional constraints

A1

Fig.9. Representation of the rule of universal quantification applied to the vectorial form.

3-

lim ⁿ^ ^t („-%)!n x    ¹

limp ^0(1 - P)x = 1

log(1 - P)n = nlog(1 - P) when n ^

P ^ 0.

to and

We deduce that

Every one of the four rules is conditioned with binary condition (true /false). The rule figure in form of ]if condition then action[every action makes new SHA to represent new nodes. This means that the probability of creating new SHAs is a Bernoulli distribution. And by iteration it becomes Binomial distribution. That means that we can calculate the number of additional SHAs by the function /like in follows.

f(xv x2, x3,x4) = Nv T^xa + N2 ^(x2) + N3 .T3(x3) + N^.T^)

p = 1-q

Where

Tt(x) = С^ .Px .(1 - P)n""x With 0

Xi success number; it represents the case conditions of rule is satisfied, n for number of iteration (experiments).

represent number of SHAs created by the when condition is satisfied.

lim    (1 — P)n = e

Il ^ t , P ^ 0, n P ^Л

when rule i

^x     x!(n-%)!

Then

Ti(x)= %^ .px .(1 - Р)^

To prove that the Algorithm will attend a stop point.

Now we accept that if all T(x) converge f converge also. And the limit of the augmentation function must be equal to “0” to riche stability case in which the inference stops.

lim%^+tT^x== lim (-Лт .Px .(1 - Р)"-X) (19) ^+t z\(n-z)\

To prove the convergence, we know that 0 < x < n that means that if x ^ +to , n ^ +to because if we like to have a big x we must have a bigger n'

Then

As conclusion

When n ^ +to, p ^ 0 and nf ^ Л where

x !(n - %)!

.Px.(1 - p)n x

Can be approximate to

е-л^^ !

Now, ^ +to , (0 < x < n )

lim%^+t T/(x) = lim e ^Л L^L = 0 n 2 x          % ^+^t     %!

We know that if every T£ (x) ^ 0 means that the Algorithm achieves stability. Other way the limit “0” means that there is no inference, no augmentation or no new deductions which means the case of stability.

The advantages of this approach is that; in one hand, it enables an easier implementation, it makes the reasoning Algorithm a simple process manipulating significant vectors, also the generation of the SHAs is computable process. In the other hand, intuitively that effectiveness will not decrease and efficiency will increase because of the use of vectors comparing which makes the algorithm leas complex.

The disadvantages are that at this time we can’t affirm that the SHAs are expressive because it is known that reducing equivalences to subsumption relationships decreases the expressivity level. But also we can’t affirm in the other hand that the representation with SHAs is leas expressive thing which is let for future study.

• IX. Conclusion

In this work we presented the SHA like new representation able to carry the semantique aspect of concept definition in ALC Languages. The vectorial form leads to simplified form of manipulation which yields to easy implementation of reasoning algorithm. The aim achieved heir is the efficiency at the level of algorithms by acting on the representation.

Computable generation process of this new representation and simplicity of manipulation of representatives vectors encourage the investigation on DLs KRS respecting this proposed approach.

The future of this proposed approach can be decided after implementation of DL system based on SHA to enable searchers to test and check all aspects like completeness and expressivity which are the main aimed goals in this field.