Proposing Two Defuzzification Methods based on Output Fuzzy Set Weights

Published Online February 2016 in MECS

Fuzzy expert systems like fuzzy controllers or fuzzy inference systems end in defuzzification. Defuzzification is the procedure of producing a crisp value out of a fuzzy set. There are several types of defuzzification methods that act based on different criteria. Most types of these methods are the kinds of maxima methods like FOM, MOM or LOM or distribution methods like COG, WA, WFM, FM or area methods like COA and ECOA that are based on fuzzy set geometry. In another point of view defuzzification methods can be divided into two groups. The first group like COG or COA act on one single fuzzy set obtained from using aggregation operators like maximum, sum and probabilistic sum of the outputs of a rule-based system. Other methods such as WFM, FM and WA act on each fuzzy set obtained from each rule using implication operator on consequent sets and then aggregate the results to make the final crisp output of defuzzification procedure. However, there isn’t any certain rule for selecting the defuzzification strategy, choosing the most appropriate technique of defuzzification depends on the properties of the application or problem, but because of some disadvantages of common defuzzification methods [1,2] we were looking for new techniques of defuzzification. In this approach two programmable methods derived from the general principle of weighting were developed. In section 2 and 3, the definition of fuzzy logic, fuzzy reasoning and mechanism of fuzzy systems are described. In section 4 defuzzification criteria and properties are discussed. In the next section some standard methods for defuzzification are reviewed. In section 6 the proposed methods will take into place by solving two important numerical examples and some standard methods are used to compare the proposed methods’ outputs in this part.

• II.    F uzzy L ogic A nd F uzzy R easoning

Logic is the study of methods and principles of reasoning, where reasoning means obtaining new propositions from existing propositions [3]. In the classical logic, a simple proposition is strictly true or strictly false [4]. It means the truth value of a proposition is a value of 1 (truth) or 0 (false). Fuzzy logic is a precise logic of imprecision and approximate reasoning [5]. It is a type of logic that recognizes more than simple true and false values. With fuzzy logic, propositions can be represented with degrees of truthfulness and falsehood in [0, 1]. This allows us to perform fuzzy reasoning. Fuzzy reasoning also called approximate reasoning [3].

• III.    F uzzy S ystems

Fuzzy systems are universal approximators [6]. With universal approximators, systems are addressed which can approximate any mapping (function). The fuzzy system can be regarded as an interpolation between numbers of points, each defined by a fuzzy rule [7].

Different researchers consider the different categories of fuzzy systems. One of these classifications is dividing fuzzy systems to two broad categories: fuzzy expert systems and fuzzy decision-making systems [8].

Fuzzy decision making systems can use a decisionmaking block or decision-making matrix instead of rule base where fuzzy expert system develops a kind of qualitative reasoning system for a specified domain of expertise [8].

Fuzzy controllers or fuzzy inference systems are types of fuzzy expert systems that in recent decades their usage in science and advanced engineering has been increased significantly. For example, in [9] usage of fuzzy inference compensator in controlling of systems with nonlinear and uncertain dynamic parameters like spherical motors, where classical methods are not efficient, has been explained. As an industrial application in [10] usage of a Fuzzy Logic Controller (FLC) in hardware implementation has been demonstrated. The FLC was designed for an armature control DC motor speed control, which led to reduction in designing time and evaluation time of the design functionality. In [11] has been described how the development of an (FLC) for a class of industrial Electro hydraulic manipulator enhances the robustness and tracking ability of the controller. In medicine Allam, F. et al. [12] used a fuzzy logic controller and a recurrent neural network to determine the insulin dosage in a closed loop blood glucose regulation system that results in decreasing the postprandial glucose concentration.

Fuzzy Outputs

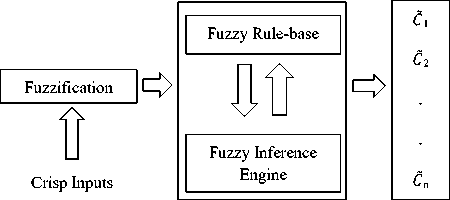
Aggregation

Fig.1. Structure of a fuzzy inference system

Defuzzification

Crisp Output

Every fuzzy expert system consists of following stages [1, 7]:

• 1.    Fuzzification of input variables by assigning overlapping fuzzy sets over each of these variables and mapping the input values into their membership grades in the input fuzzy sets.

• 2.    Providing connection between input and output fuzzy sets by applying the inference rules in the form of IF-THEN rules. Fuzzy connectives (AND & OR) are used in IF part of the rules.

• 3.    Implications from IF parts toward THEN parts of the rules. In this part the degree of fulfillment for the each rule is determined, where fuzzy sets C i are assigned to the universe of discourse of the output variable.

• 4.    Aggregation of THEN parts of the rules which are the results of individual rules into one output fuzzy set Cʹ.

• 5.    Defuzzification the output fuzzy set into the crisp output value.

• IV.    D efuzzification

Defuzzification is a mathematical process used to convert a fuzzy set or fuzzy sets to a crisp point. It is a necessary step because fuzzy sets generated by fuzzy inference in fuzzy rules must be somehow mathematically combined to come up with one single number as the output of a fuzzy controller or model [3].

• A.    Defuzzification Properties

Runkler T. A [13] mentioned that whereas a defuzzification operator selects significant crisp value it needs to have some basic properties. He considered two main categories of them: theoretical interest and application orientated ones and separated them into static, dynamic, statistical and implementation properties.

Runkler describes some important properties of the defuzzification process as follows:

• 1.    Consistency: when a defuzzification maps convex crisp sets to their centroid, it is called consistent.

• 2.    Section invariance: When a magnification of a regarded section, does not affect the results, the defuzzification is called section invariant.

• 3.    Monotonicity: If the defuzzification result remains unchanged or moves toward a single element when its membership grade increases or if by decreasing the membership grade of a single element the defuzzification result moves to the opposite direction or remains constant it is called monotonous defuzzification.

• 4.    Linearity: A linear defuzzification result is maintained after affine transformation such as rotation, reflection, translation and scaling.

• 5.    Offset and scale invariance: if membership values offsets or scaling does not affect the defuzzification result, it is called offset invariant defuzzification and scale invariant defuzzification respectively.

• 6.    Compatibility: the defuzzification method chosen must be compatible with the inference, composition, and other operators used in the fuzzy

• 7.    Arithmetic compatibility: A defuzzication is arithmetically compatible, if it defuzzifies “about a” to “a” which equals to the mean value with a membership grade of 1.

• 8.    Exclusion: in exclusive defuzzification methods negative information is recognized with a nonzero membership value.

system.

• B.    Criteria for Defuzzification

In [14] Leekwijck and Kerre discussed some criteria for defuzzification. Their research wasn’t based on finding the best defuzzification strategy, but they believed that for each type of application some properties of a type of defuzzification are important. Some of these criteria are generalization of a selection of the defuzzification criteria for fuzzy numbers that were proposed by Runkler and Glesner in [15].

In their paper Runkler and Glesner developed a mathematically motivated set of 13 constraints characterizing rational defuzzification strategies under 4 groups of: Basic constraints, graphically motivated constraints, constraints motivated by fuzzy operations and constraints related to specific applications. Table 1 shows the several groups that they considered in defuzzification criteria based on the mathematical structure that is needed in the universe X in order to be able to formulate the criteria.

Table 1. Several groups of defuzzification criteria

Criteria			Index
	Core selection		C1
		Ordinal scale	C2
Universe with arbitrary scale	Scale invariance	Interval scale Ratio scale	C3 C4
		Relative scale	C5
		Absolute scale	C6
Universe with ordinal	Monotony		C7
scale	Triangular conorm criterion		C8
	X-Translation		C9
Fuzzy quantities	X-Scaling		C10
	Continuity		C11
	Computational efficiency		C12
Miscellaneous	Transparency for system		C13
	design

• C.    Evaluation of Defuzzification Operators

Leekwijck and Kerre [14] classified the most widely used defuzzification methods into four different groups of maxima methods, distribution methods, area and miscellaneous methods. Then for each operator they determined the criteria that it uses for defuzzification procedure. In their classification, general defuzzification techniques and specific ones and also basic defuzzification operators and extended ones are distinguishable. Table 2 shows this classification generally (For more details and explanations see [14]). The maxima methods are good candidates for fuzzy reasoning systems while distribution methods and the area methods exhibit the property of continuity that makes them suitable for fuzzy controllers.

• V. R eview of S ome E xisting D efuzzification M ethods

In this section the formula of the most widespread defuzzification methods are presented. Most of these methods are used to verify the outputs of our proposed techniques later. To have a better understanding of differences between several strategies for defuzzification of the output of a rule-base fuzzy system, some parameters and variables need to be defined, which are commonly used in defuzzification formulas as follows:

C _K : fuzzy output set or the consequent fuzzy set after applying an implication operator.

Cʹ : the aggregated (overall) diagram of fuzzy output (as a result of the inference) sets using maximum operator.

Cʹ_k : the k^th segment of Cʹ.

ц _с ,_к 00 : the function of k^th segment of C’_k.

a_k : the pre-calculated numerical value of the output set C _k.

a_k : the degree of each consequent fuzzy output set C_k . w_k : weighted associated with each C_k.

X* : defuzzification output of Cʹ.

• •    Centre of gravity (COG) or Centroid: X* is the point along the X axis about which the area would balance.

J_c, x.^_c^ ( x ) dx 0 ц_с,_к ( x ) dx

• •    Bisector or center of area (COA): X* is the point along the X that crossing line parallel to µ axis divides the total region of Cʹ into two sub-region of equal area.

z ( COA ) _c,                    zN

J  x.^ (x) dx = J  x^C' (x) dx zin                       Z ( COA ) c'

• •    Weighted average method (WAM): this method is valid for symmetrical output membership functions. It is less computationally intensive and produces results very close to COA method. Weighting each function in the output by its respective maximum membership value.

Z N 1M x k ) . x k

Z N= A • (xk)

Where j t _k is the length of symmetry axis of C_k and N_c is the number of fuzzy output sets.

• FM (fuzzy mean): this method uses pre-calculated numerical values (ak) for each of fuzzy output sets.

E N _ k^a . ak X = ---- Гг----- N_c

X k a

Table 2. Criteria of different defuzzification methods

Type of defuzzification method	Name of defuzzification method		Abbreviation	Criteria
		Random Choice Of Maxima	RCOM	C1
Maxima methods and	Basic-General	First Of Maxima	FOM	C1, C2-C6, C7,C8, C9
derivatives		Last Of Maxima	LOM	“
		Middle Of Maxima	MOM	C1, C2-C6, C7, C9
	Basic-General	Mean Of Maxima	MeOM	C1,C2-C6, C7, C9, C10
		Centre Of Gravity	COG	C4,C7, C9, C10, C11
		Basic Defuzzification Distributions	BADD	“
	Extended-General	Generalized Level Set Defuzzification	GLSD	“
Distribution methods and derivatives		Indexed Centre Of Gravity Semi-Linear Defuzzification	ICOG SLIDE	““
	Basic-Specific	Fuzzy Mean	FM	“
		Weighted Average Method	WAM	“
	Extended-Specific	Weighted Fuzzy Mean Quality Method	WFM QM
		Extended Quality Method	EQM	“
Area methods	Basic-General	Centre of Area	COA	C4, C6, C7, C9, C10, C11
	Extended-General	Extended Centre of Area	ECOA	“
Miscellaneous methods	Basic-General	Constraint Design Defuzzification Constraint Clustering Defuzzification	CDD FCD

• •    Weighted fuzzy mean (WFM): this method is parameterized state of the FM method where w_k is the weight associated with fuzzy output set equals to the area of C_k (K t fuzzy output). By using this method a degree of importance can be assigned to each output set .

Nc

*^ X k = 1 w k a . a k

Nc

X k = 1 w k ^a k

• •    Quality Method (QM): the aim of QM is to increase the importance of the “more crisp” output sets. Where, d k equals the width of the support of C _k . It is a special case of WFM where w_k=1/d_k.

  X ^*

  
  
  
  
  
  
  
  

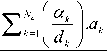
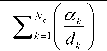
• •    Center of Largest area: if the output fuzzy set has at least two convex sub-regions, defuzzifies the largest area using centroid.

• •    LOM (largest or last of maxima): determine the largest value of the domain with a maximized membership degree.

• •    MOM or Mean-max membership: determines the middle of maximum.

• •    SOM (Smallest of Maximum) or FOM (first of maxima): determine the smallest value of the domain with a maximized membership degree.

• VI.    P roposed M ethods

• A.    Why do We Need a New Method?

Trying to find a defuzzification technique that:

• 1.    Follows the weighting principle in defuzzification procedure considering original consequent functions.

• 2.    Defuzzifies the final shape obtained from the aggregation of implicated consequent functions, so unlike methods like FM, COS or WFM eliminates errors arising from overlapping of output functions and also unlike some kind of methods like WAM, be valid for both symmetrical and non-symmetrical output functions.

• 3.    Unlike methods like center of largest area, SOM, LOM or MOM, defuzzifies the total aggregated function not part of it.

• 4.    Small changes in fuzzification don’t result in big changes in defuzzification stage.

The proposed defuzzification methods are introduced in this section by considering:

Cʹ : the aggregated (overall) diagram of fuzzy output (as a result of the inference) sets using maximum operator.

Cʹ_k : the k^th segment of Cʹ.

Ц_с, ( X ) : the function of k^tth segment of C_k.

Following parameters are defined:

w'_k: weight associated with k^th segment of C'.

A'_k = j ^ , ( x ) dx: the area under k^tth segment of C'.

_ Jc x.^.,t (x) dx : centre of gravity along X axis k J^c, (x) dx associated with C'k.

The general formula of proposed methods is presented as:

The general formula shows that this technique is kind of weighting method. By assigning weights associated with segments of the ultimate aggregated diagram of fuzzy output sets using the maximum operator, this method looks more like the COG method than WFM. The main characteristic of this method is the weight w ' which is calculated by considering another aggregated function C and its related parameters as following:

C: the aggregated (overall) diagram of consequent fuzzy sets (before applying the implication operator) using maximum operator.

C_k : the k^th segment of C.

у  ( x ) : the function of C_k

The weight W'_k for each segment is obtained by computing a ratio associated with attributes of C_k and C'_k to each other. We propose two different W'_k derived from these attributes.

• B.    Proposed method (1)

In the first proposed method , _ Hg■ _k is replaced in ^у .

the equation (7), so we will have:

Z k = 1 ” /.^J c x T . ( ^x ) dx           (8)

^Gk z k '  .^.л x) dx

^Gk

Where:

J Г У (x ' ' dx „        ,     .    , c     2         : Centre of gravity along µ

Gk     Jc Tk (x) dx axis associated with Ck.

. Г t ( x )T

L Лс» у vj dx c'     2         : Centre of gravity along µ

J

^T G \? =

^J c A c 4 ( ^x ) ^dx

axis associated with C' k .

In this method, for each segment of C' k , the vertical centre of gravity along the µ axis is calculated for the areas under the functions y ( x ) and у ( x ) and then w'_k is calculated by dividing the obtained values. In figures 2.c and 3.c, functions y ( x ) and Ц_с, ( x ) have been illustrated with solid line and dashed line respectively.

• C.    Proposed Method (2)

In the second proposed method w - = A . is replaced k   Ak in the equation (7), where:

A_k = J_c y ( x ) dx : the area under k^th segment of C .

A '_k = J_c, у ( x ) dx : the area under k^{t h} segment of C .

, У n W . A ‘. a ‘

*          k = 1   .   .   .

n W- A‘ k=1  k k

So:

, = J cTc' k ( x ) dx k Jc У (x) dx and:

n J c. yc, k (x) dx ,           ,.

Y. Zk=1 JcT4 (x) dx •J c'xTc'k (x)dx(9)

^{Z k} = 1 J у ( x ) dx •^{J с У с} • ^{k ( x} ) ^dx

In this method, for each segment of C'_k , the area under the functions ц._Ск (%) and ц _с,_к (x), shown as a. and A’ _k respectively, are calculated and then the related weight is obtained.

• D.    Numerical Example (1)

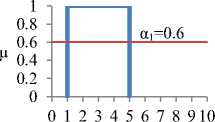
In this example, the output of fuzzy set illustrated with a solid line in figure 2.c is found using the proposed methods. This set is the outcome of implication and aggregation procedures of symmetrical fuzzy sets shown in figures 2.a and 2.b. The defuzzification is performed in three situations of α cut .

• •    Solving the example using the proposed method (1), where : w. = ^ Z l

0.3

^Gt

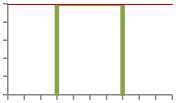
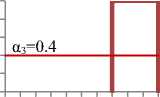
As shown in Fig. 2.a. in situation (1) where: α1=0.6, α2=1, α3=0.4, the elements of equation (7) are calculated as follows:

To calculate w ' :

^T G 1    ^T G ₂   ^T G 3   ^0.5

^T G 'i ? = 0.3’ ^HG_t = 0.5’ M'Gk = ^0.2

( y^ is center of gravity of C_k and y_k. is center of gravity of C' k along µ axis) So:

w ‘ =---

¹    0.5

0.5 '

= 0.6, w ‘ =    = 1, w.

^{,   2}     0.5      ^{,    3}

02 = 0.4

0.5

So:

A k = ^J c M c,\ ^x ) dx

elements of equation (7) are calculated as follows:

To calculate w ' we have:

Ak =Jc'^Ax) dx

So:

A ; = J 0.6 dx = 1.2, A = J 1 dx = 4, A ; = J 0.4 dx = 1.2

So:

a'k

Jc, x.^ (x) dx

J c ^c'k ( x ) dx

3                           7                    10

A = J 0.6 dx = 1.2, A = J 1 dx = 4, A'₃ = J 0.4 dx = 1.2

1   37

Ak = Jc Mc„ (x )dx

So:

3 0.6 xdx '1' ^a 1       3              z., a,

J 0.6 dx

⁷ xdx ' 3

' 2         7

J 1 dx

0.4 xdx

= 5, a 3 =           = ^8.5

J₇ 0.4 dx

3                     7                    10

A = J 1 dx = 2, A = J 1 dx = 4, A = J 1 dx = 3

So:

By replacing the obtained values in equation (7) we have:

x *_ Ekwk -Ak.ak

X = Ek=wk Ak

So:

.  ( 0.6 x 1.2 X 2 ) + ( 1 x 4 X 5 ) + ( 0.4 x 1.2 x 8.5 )

X =-----7-------x—7---x—7-------x-----= 4.907

( 0.6 x 1.2 ) + ( 1 x 4 ) + ( 0.4 x 1.2 )

• •    Solving the example using the proposed method '

(2), where: w '

^k A k

In situation (1) where: α1=0.6, α2=1, α3=0.4, the w =

1.2              4       '

--= 0.6, w‘ = — = 1, w, ==

2        ,2    4    ,3

We have a ' (centre of gravity along x axis associated with C'k ) from the previous section. By replacing the obtained values in equation (7) we have:

* ₌ ^E k = w k "A k . a k " E k = w k A k

So:

. _ ( 0.6 x 1.2 x 2 ) + ( 1 x 4 x 5 ) + ( 0.4 x 1.2 x 8.5 ) _

X =       ( 0.6 x 1.2 ) + ( 1 x 4 ) + ( 0.4 x 1.2 )       = ^4.907

CMF1

X

µ

CMF2

α 2 =1

1 0.8 0.6 0.4 0.2

0 1 2 3 4 5 6 7 8 910

X

CMF3

0.8

µ 0.6

0.4

0.2

0 1 2345678910

X

Fig.2.a. Implication of consequent membership functions (CMF) applying different cuts of α: situation (1): α1=0.6, α2=1, α3=0.4

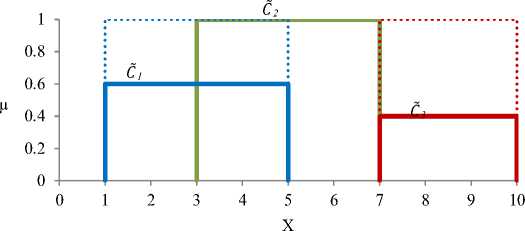
Fig.2.b. Aggregating of implicated fuzzy output and consequent sets

0.8

0.6

µ 0.4

0.2

C 1

C 3

C' 2 = C 2

C' 1

C' 3

0      1      2      3      4      5      6      7      8      9     10

X

Fig.2.c. Aggregated fuzzy sets of consequents and fuzzy output sets

We solve this example in two more α-cut situations:

• Situation 2: a 1 =0.6, а₂=1, а3=1

Proposed method (1):

Proposed method (1):

w ² =

0.5

0.5

⁷2 =

0.5

0.5

0.5

’₃ =     = 1

³    0.5

So:

0.3            0.50.5

w. =    = 0.6, w0 =    = 1, w, ==

1   0.5         2   0.5       3

So:

,   ( 1 x 2 x 2 ) + ( 1 x 4 x 5 ) + ( 1 x 3 x 8.5 )

X =      (1x2)+(1x4) + (ix3)

,   ( 0.6 x 1.2 x 2 ) + ( 1 x 4 x 5 ) + ( 1 x 3 x 8.5 )

X =------;-----   / z -------;------ = 6.08

( 0.6 x 1.2 ) + ( 1 x 4 ) + ( 1 x 3 )

Proposed method (2):

^w 1 =

— = 1, w 2

Proposed method (2):

; = 3 = 1

So:

1.2              4        '     3

w = —= 0.6, w = - = 1, w 3 = - = 1

So:

.   ( 0.6 x 1.2 x 2) + (1 x 4 x 5) + (1 x 3 x 8.5

X = ------;-----⁷ ? _z-------;-----⁷ = 6.08

( 0.6 x 1.2 ) + ( 1 x 4 ) + ( 1 x 3 )

• Situation 3: a1=1, a2=1, a3=1

„ _ ( 1 x 2 x 2 ) + ( 1 x 4 x 5 ) + ( 1 x 3 x 8.5 ) _

^X =      ( 1 x 2 ) + ( 1 x 4 ) + ( 1 x 3 )       = ^5.5

In this example, both proposed methods for every particular situation of α-cuts, result in the same values.

A comparison between defuzzification values using the proposed methods with some common methods for this example has been illustrated in Table 3.

• E.    Numerical Example (2)

  In this example the defuzzification of fuzzy set illustrated with a solid line in figure 3.c is performed using the proposed methods. This fuzzy set has been obtained through implication and aggregation of 3 non-symmetrical fuzzy sets presented in figures 3.a and 3.b.

  
  
  
  
  

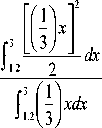
  = 0.37, M_G, =

  
  

  ■ 3.4 [ 0.5 x + 2.5 ] ²^ ³2 ^x

  3.4

  f 0.5 x + 2.5 dx

  
  

  = 0.45

  
  

  • • Solving the example using the proposed method

  • (1), where: w - = "GV ( ^ is center of gravity of

  " G -

  C k and ^ ,_t is center of gravity of C - along ^ axis).

  f. [ * I² dx ^M=- = f , " „ ( x ) dx

  So:

  
  

  ,4 [ - 0.5 x + 2.5 ] ² dx

  ^f 3.4           2

  - 0.5 x + 2.5 dx

  3.4

  
  
  

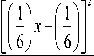
  - 0.5 x + 1 dx

  
  

  = 0.33, Mc_t =

  
  

  о. = 4Ц---- ²-------- = 0.408, д.

  G ₇             7                                          G ₈

  
  

  4.6

  
  
  
  
  

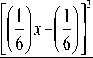
  4.6

  dx

  
  
  

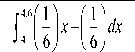
  = 0.275

  
  
  
  
  

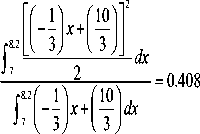
  [ 06              ] dx

  ^ = —-- ²----- = 0.429, ^

  G ₁             0.6                                              G ₂

  - 0.5 x + 1 dx

  
  

  ■ 1.2 [ - 0.5 x + 1 ] 2 0.6         ₂

  
  

  dx

  
  

  1.2

  - 0.5 x + 1 dx

  0.6

  
  

  = 0.281

  
  
  
  
  

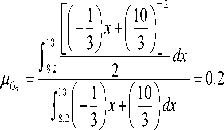
Table 3. Different methods’ results of defuzzification for example 1

			Common defuzzification methods outputs						Proposed methods outputs
									Ц сгк	,     A' k
Situation α 1 =0.6	COG	COA	WAM	WFM	FM	SOM	MOM	LOM	w' =  - ^ Gk	w'k = k    Ak
α 2 =1 α 3 =0.4 α 1 =0.6	5.093	5.00	5.1	4.92	5.1	3	5	7	4.907	4.907
α 2 =1 α 3 =1 α 1 =1	5.84	5.9	5.88	5.6	5.88	3	6.5	10	6.08	6.08
α 2 =1 α 3 = 1	5.5	5.5	5.5	5.22	5.5	1	5.5	10	5.5	5.5

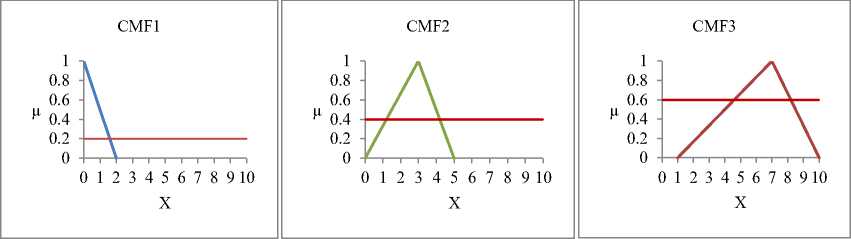
Fig.3.a. Implication of consequent membership functions (CMF) applying different cuts of α.

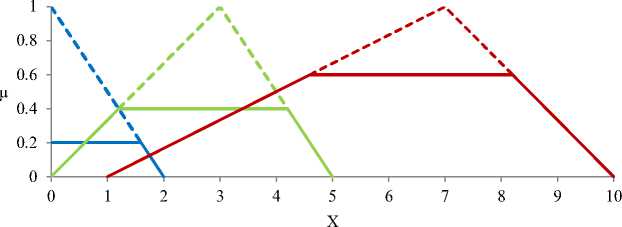
Fig.3.b. Aggregating of output and consequent fuzzy sets

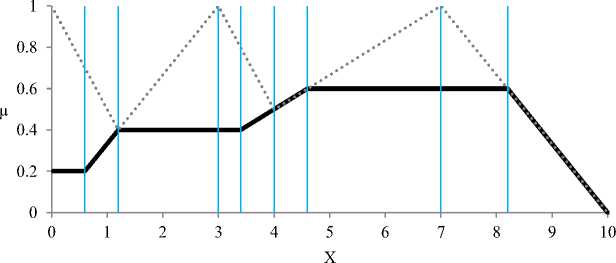
Fig.3.c. Aggregated fuzzy sets of consequents and fuzzy output sets

So

M g 1

M g ‘ 3

	MG'k
f 06 12:2 1 : dx 0 2
	0.6 0.2 dx 0
J	з [ 0.: ] 2 1.2     2	dx
	0.4 dx 1.2
f :,	к 6 ) x -( 6 ): 2	2 dx

0.1, MG,

^M G =   f :■ ( 6 ) x -( 6 ) dx

f,. [ ^{M c}‘ ^{( x} ) ]² dx c      ₂

f c M c_k ( x ) dx

= 0.2, M e

= 0.226, ^, =

Г (	^ I2
	) x .

1.2

0.6      ₂

dx

— = 0.155

xdx

j⁷ [06 : dx

4.6    2

Mg- 7        7               0.3, M g '8

0.6 dx

4.6

[": dx

----= 0.175

J 0.6 dx

j

^M g 9 =

8.2

(-3И7

с(-з)»(?) dx

dx

= 0.2

Mg,

Now we can calculate the weights: w '

34 10^ dx

3.4	= 0.2	0.1	0.155	0.2
? dx		w \ =----	= 0.233, w 7 =	= 0.55, w \ =----=
3		1    0.429	2    0.281	3   0.37
[ ( 6 ) x -( 6 ) ]2. dx		0.2 w 4 = 4    0.45	0.226 = 0.44, w ^ 5 =------: ,    5     0.33	0.275 = 0.684, w 0 =----- ,    6    0.275

0.54

4.6

= 1

f: ( 6 И 6 )

— = 0.275 dx

0.3               0.175              0.2

w ₇ =----= 0.735, w „ =-----= 0.428, w „ = — = 1

7   0.408           8  0.408           9   0.2

In the next step, A ‘ is calculated:

The final crisp value of defuzzification is obtained:

Ak  JcHc^x) dx

X * = 5.48

• Solving the example using the proposed method

So: A \ = _f 0.2 dx = 0.12, A ‘ = J f 1 ³ xdx = 0.18 0                         0.6 ^{C 3 )}

(2), where: _{w '}

A '₃ = J 0.4 dx = 0.72, A \ = J 0.4 dx = 0.16

3.4

segment of C segment of C' ).

= A k (Ak : the area under kh Ak and A ' is the area under kth

1.2

A '5=i c 6 ) x -c 6 ) d^x = °.^27, A *=I c 6 ³ x -c 6 ) dx =    3

We have A ' from the previous section. The formula for calculating A_k is: A_k = J_CH_C ( x ) dx so we have:

0.6

1.2

4.6

8.2

= J 0.6 dx = 0.72

A = J - 0.5 x + 1 dx = 0.51, A = J - 0.5 x + 1 dx = 0.33

0.6

A '9 "I C ^- 33 x ⁺ 130) d^x = ^0.54

A = J ⁰ 1 ³ xdx = 1.26, A = J 0.5 x + 2.5 dx = 0.36

1.2 ^{C 3 )}                        3

J_C' x . H ' ( x ) dx •     1   1 j

Then, a' = —___ ^{c k v} ___ is calculated:

k J c ' H c \ ( x ) dx

A = J 0.5 x + 2.5 dx = 0.39, A = J f | | x -0 1 | dx = 0.33

0.6

J 0.2xdx a '1 = 706------= 0.3, a2 =

0.2? dx

I ^xdx               [3 0.4 xdx

⁾— = 0.933, a '₃ =   ------= 2.1

xdx              J 1, ^dx

A = J ^C 1 | x -^C 1 | dx = 1.92, A = J ^f- 1 | x + ^f у ³ dx = 0.96

dx = 0.54

8.2

3.4

I  0.4xdx a 4     r3.4            J ,a 5

J 0.4 dx

J 4 x • [C 6) x -C 6 )]

^{J 4}4 ^C6) x -^C6^ dx

dx

= 3.71

Now we can calculate the weights: w ' = A k k   Ak

w \ = 0.12 = 0.235, w '₂ = 0.18 = 0.545, w '₃ = 0.72 = 0.57

¹    0.51             ²    0.33             ³    1.26

a V, =

J :46) x -f 6)]

^J-6 [ 6) ^{x -f} 6) dx

dx

= 4.31, a '₇ =

⁷ 0.6 xdx

4^ -----= 5.8

0.6 dx

4.6

0.16 w = 4   0.36	= 0.44, w '5	0.27 0.39	= 0.69, w '6	0.33 0.33
1.44 w' =---- 7    1.92	= 0.75, w '8	0.72 = 0.96	= 0.75, w '9	0.54 = 0.54

= 1

= 1

By placing the obtained values in:

8.2

J 0.6xdx a 'я =    ------= 7.6, a \ =

88.2                         9

J   0.6 dx

j:<- 3 ) x +f 10 )

J 80 (-3) x +(I ) dx

dx

= 8.8

_x * ₌ Z k = w ' k - A ' k . ^a ' k Z k = w ' k . A ' k

By placing the obtained values in:

The final crisp value of defuzzification is obtained:

X ^*

z k = w ’ k A' k a' k z k = w ' k A ' k

X * = 5.61

A comparison between defuzzification values using the example has been illustrated in Table 4. proposed methods with some common methods for this

Table 4. Different methods’ results of defuzzification for example 2

Common defuzzification methods outputs	Proposed methods
Situation   COG   COA     WFM     FM   SOM   MOM   LOM	- Mc ' k       - 'G Wk = V  v/' ^ Gk            ^ k
α 1 =0.2 α 2 =0.4       5.18     5.37         4.84        3.81      4.6       6.4       8.2 α 3 =0.6	5.48           5.61

• VII.    C onclusion

The final output of a fuzzy system is determined through defuzzification procedure so the applied method for defuzzification plays a significant role in how outputs of a fuzzy system are accurate and efficient. This study was performed as an effort for finding new methods and techniques for defuzzification which may result in more precise results.

The proposed methods in this study parameterize the COG of aggregated fuzzy set by applying weights produced through mathematical calculations considering the implicated and original consequent membership functions simultaneously. In the first method the assigned weight is produced by calculating the ratio of center of gravity along the vertical axis (µ) for each specific range of horizontal axis (x) on aggregated fuzzy sets of implicated and original consequent membership functions and in the second method the COG is weighted by the ratio of the area under the mentioned functions in respect to each horizontal range. Through the first numerical example, it was simply showed how these methods work.

One single shape derived from aggregation of three simple and symmetrical output functions was defuzzified in three states of implication and compared the results with some existing defuzzification methods. Thus, unlike WA, FM and WFM methods that act on each implicated consequent function separately, overlapping of consequent membership functions does not affect the output value in the proposed methods. In the second numerical method the differences between these methods and COG can be understood and the limits that the calculations are performed on both original and implicated consequent functions can be realized.

Synthese, 30 (1975), pp. 407–428.

Kosko, B., Fuzzy systems as universal approximators , IEEE Transactions on Computers, Vol. 43, (1994), pp. 1329-1333.

R. Jager, Fuzzy logic in control , Ph.D. dissertation, Tech. Univ. Delft, Delft, The Netherlands, (1995).

Saletic, D. Z., Velasevic, D. M., Mastorakis, N. E., Analysis of Basic Defuzzification   Techniques ,

Proceedings of the 6th WSES International Circuits, Systems, Communications and Computers, CSCC 2002, Rethymnon, Greece, (July 2002).

Siahbazi, A., Barzegar, A., Vosoogh, M., Mirshekaran, A. M., Soltani, S .,Design Modified Sliding Mode Controller with Parallel Fuzzy Inference System Compensator to Control of Spherical Motor , IJISA, ,vol.6, no.3, (2014), pp.12-25.

Shankar Anand,  M., Tyagi, Ba., Design and

Implementation of Fuzzy Controller on FPGA , IJISA, vol.4, (2012), no.10, pp.35-42.

• A. Aly, A., S. Abo El-Lail, A., A. Shoush, K., A. Salem, F., Intelligent PI Fuzzy Control of An Electro-Hydraulic Manipulator , (2012), IJISA, vol. 4, no. 7, pp. 43-49,.

Allam, F., Nossair, Z., Gomma,  H.,  Ibrahim, I.,

Abdelsalam, M., Evaluation of Using a Recurrent Neural Network (RNN) and a Fuzzy Logic Controller (FLC) In Closed Loop System to Regulate Blood Glucose for Type-1 Diabetic Patients , IJISA, vol.4, no.10, (2012), pp.58-71,. Runkler, T. A., Extended Defuzzification Methods and their Properties, IEEE Transactions, (1996), pp. 694-700. Leekwijck, W. V., Kerre, E. E., Defuzzification: criteria and classification , Fuzzy Sets and Systems, Vol. 108 (1999), pp. 159-178.

Runkler, T. A., Glesner, M., A Set of Axioms for Defuzzification Strategies Towards a Theory of Rational Defuzzification Operators , Proceedings of the IEEE International Conference on Fuzzy System, (1993), pp. 1161-1166.

• [1]    Saade, J. J., Diab, H. B., Defuzzification Methods and New Techniques for Fuzzy Controllers , Iranian Journal of Electrical and Computer Engineering, Vol. 3, No. 2, (2004), pp. 161–174.

• [2]    Mukherjee, S., Bhattacharyya, R., Kar, S., A Novel Defuzzification Method Based on Fuzzy Distance ,

  International Journal of Fuzzy Systems and Rough Systems (IJFSRS),Vol. 3, No. 1, (Jan-Jun 2010).

• [3]    Zhang, H., Liu, D., Fuzzy Modeling and Fuzzy Control , Birkhauser, Boston (2006), p. 16.

• [4]   Timothy, J. R., Parkinson, W.J., Fuzzy Logic and

  Probability Applications , 2002, Chapter 2, pp. 29-43.

• [5]  Zadeh, L.A., Fuzzy logic and approximate reasoning ,