Пропускная способность конусных затворов
Автор: Подрубалов М.В.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Технические науки
Статья в выпуске: 10-5 (97), 2024 года.
Бесплатный доступ
В статье представлены результаты опытного исследования пропускной способности конусных затворов. Рекомендуется таблица и формула для определения коэффициента потерь затворов фирмы CAMOZZI и подобных им затворов других фирм.
Затворы, пропускная способность, коэффициент потерь, потери в течении трубопровода, экспериментальные исследования
Короткий адрес: https://sciup.org/170207080
IDR: 170207080 | DOI: 10.24412/2500-1000-2024-10-5-36-41
Текст научной статьи Пропускная способность конусных затворов
С целью исследования пропускной способности конусных затворов фирмы CAMOZZI была изготовлена опытная установка напорного водовыпуска, завершающегося конусным затвором.
Схема исследованного конусного затвора показана на рис. 1 и имеет следующие без- размерные параметры: угол конусности а = 0,873рад = 500; отношение максимального открытия к диаметру затвора Qmax/d0 = 0,625; отношение диаметра обтюратора к диаметру затвора do6T/d0 = 1,10.
Рис. 1. Схема конусного затвора
Вначале был установлен вид расчетной формулы [1, 2, 3, 4] расхода системы напорная галерея – конусный затвор. Из уравнения
Бернулли, примененного к верхнему бьефу водовыпуска и к сжатому сечению потока на выходе из затвора (рис. 2), следует:
Eo=Ec+Shnp,
где: Eo = Н, т.е. превышению уровня верхнего бьефе над осью затвора.
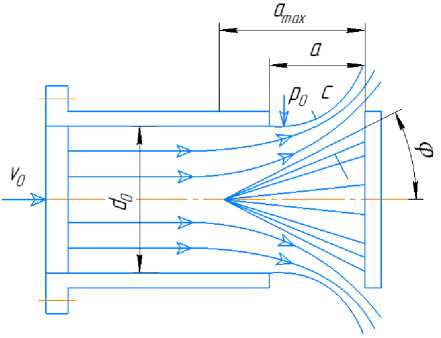
Рис. 2. Сечение потока на выходе из затвора
Ввиду того, что в сжатом сечении струи после затвора давление атмосферное, то двучлен z+p/γ не постоянен и поэтому удельная энергия имеет различные значения для различных секторов кольцевого сечения. В урав- нении (1) величина Ес является средним значением удельной энергии в сжатой сечении определяемым выражением:
Ес=-1( (vEdQ) = 1 f (г* cos(a) + acVc\ dp*r*8*vc =
a v 2
с C-(2)
2q
YqJ QJ(p=o к 2q J Подставив в (1) значения Е0 и Ес, а также ных решеток до конусного затвора и потери подставив потери как сумму потерь от вход- получим: и _ acVC , _ fwoV VC VC [ ZWA2! /затв * vC Н 2q (EhTp\™ + hзатв ac (wc) 2q + 2q П (WC) Ц + 2q или и VC\\yi ^oX2] . (^о\2 13атв * vC] H = 2qT'UL + acU +^Н'(3) где v0 и w0 - средняя скорость м площадь живого сечения на входе в аатвор, Vc и Wc -соответственно коэффициент Кориолиса и площадь в сжатом сечении струи после затвора, а 1затв - коэффициент потерь затвора. Раздельное определение коэффициентов ac и 1затв и отношения w0/wc весьма затруднительно. В то же время для расчетов пропускной способности [1, 2, 3, 4] достаточно знать полное значение суммы в квадратных скобках, которую обозначим: I затв aC(w0/wC) + ^затв- Выражение для расхода будет иметь вид: Q Есист * W0 * ^2qH, (Л) где: _ 1 ^\ЕЦ * (wo/wC)2]зал + ^затв В задачу экспериментального исследова- Для получения рабочего выражения по иссле-ния [2] входило изучение коэффициента 1’затв. дованию этого коэффициента достаточно в уравнении (3) за первое сечение принять этом случае: входное сечение затвора. Считывая, что в „^^„^ру =о, (6) получим: Г 2Ч ''"«Лал ^-Й-К".......I (7) На практике конусные затворы располагаются в конце достаточно длинных прямолинейных участков, а числа Рейнольдса не их входе бывают весьма велики [3]. Поэтому во входных сечениях затворов следует ожидать равномерное распределение скоростей со значением а0 — 1,0. Г = затв 1 + Ро/;ц2 к/ 2ч' где: — и^ — пьезометрические высота и скоростной напор на входе в затвор. Выражение (7) было использовано как рабочее для исследования коэффициента Гзатв. Учитывая весьма высокие значения чисел Рейнольдса на входе в затвор в натурных условиях и усиленную дополнительную турбулизацию потока при обтекании лопастей затвора, можно не сомневаться, что конусные затворы в натуре работают в автомодельной области. Таким образом, наряду с обеспечением прочих условия моделирования, экспериментальная установка должна была обеспечить равномерное распределение скоростей на входе в затвор и автомодельность движения в слом затворе за сечением I - I (рис. 2) [4]. Соответствующие измерения и проверки показали, что установка удовлетворяла этим условиям (рис. 3). Рис. 3. Экспериментальная установка Приступая к экспериментальному исследованию, следует также наметить те граничные факторы, которые могут существенно влиять на искомую величину. И данном случае такими факторами могут быть число Рейнольдса и коэффициент Кориолиса во входном сечении затвора, относительная шероховатость и относительное открытие [5]. Первые трм факто- ре отпадают по следующим причинам: число Рейнольдов – ввиду автомодельности, коэффициент Кориолиса – ввиду его постоянства (а0 — 1,0 — const), относительная шероховатость – ввиду того, что конусный затвор, обладающий сам по себе весьма гладкой внутренней поверхностью, является типичным случаем местного сопротивления. Таким об- разом, из всех перечисленных выше факторов следует иметь в виду лишь относительное открытие затвора ] = d/amax. В соответствии со сказанным все опыты были разбиты на 9 серий, соответствующих относительным открытиям ]= 1,00; 0,70; 0,50; 0,40; 0,20; 0,10; 0,06; 0,04; 0,02. Значение чисел Re во входном сечении затвора в опытах менялось в пределах Re = 20000 + 405000 при общем числе опытов 78. Сравнение значений коэффициента /’затв для различных опытов одной и той же серии [2], выполненных при различных значениях числа Re, но при одинаковых значениях ]=const , показало, что значения коэффициента /'затв не зависят от ыеняющнхся значений числа Re. Так, например, в серии ] =0,40 чис- Опытное значения коэффициента Гзатв приведены ниже в таблице 1. Ввиду того, что в натуре как турбулизация потока, так и тенденция к выравниванию скоростей на входе в затвор будут еще более сильно выражены, то информация относи- ло Re менялось в интервале Re = 145000 … 210000, т.е. на 41,5 % в то же время опытное значение /'затв колебалось вокруг среднего значения 1'затв= 6,00 со среднеквадратичным отклонением ±0,66%. Аналогичная картина наблюдалась также и во всех других сернах [6]. Таким образом, опыты действительно проводились в автомодельной области, и модельная установка удовлетворяла этому предварительно поставленному условию. Сравнение значений коэффициента Гзатв различных серий [2], отличающихся различными значениями относительного открытия ] показало, что последнее является единственным аргументом, практически определяющим значения Гзатв автомодельной области, т.е.: /'затв = f(]Y (7) тельно уравнения (7), содержащаяся в таблице 1, универсальна для всех конусных затворов для подобных им конусных затворов других фирм [4]. Математическая обработка данных [2] таблице 1 показывает, что уравнение (7) примет вид: Гзатв = 1,68(1/])1,47. (8) Таблица 1. Сравнение значений коэффициента /'затв различных серий Постоянные параметры: d0 = 80мм; атах 50мм; t0C = 250.Серия Количесво опытов т Г с затв Re*10-6 /’затв расч. 4Q 1 7 1,0 1,68 0,321...0,405 1,68 0 2 10 0,7 2,61 0,245...0,317 2,85 -4,3 3 5 0,5 4,70 0,165...0,238 4,65 +0,5 4 6 0,4 6,00 0,145...0,21 6,46 -3,8 5 10 0,2 18,94 0,1...0,093 17,9 +2,7 6 10 0,1 55,05 0,068...0,06 49,6 +5 7 10 0,06 112,32 0,053...0,043 105 +3,3 8 10 0,04 175,84 0,04...0,03 190 -4 9 10 0,02 537,26 0,025...0,02 532 +0,5 Джи оценки соответствия формулы (8) опытным данным следует сравнить значения расхода [6], пожученные по зависимости (4) при подстановке опытных значений Гзатв, c значениями, полученными по (4) при подстановке значении 1’затв согласно (8). Процент- ное расхождение между экими двумя расхо- дами будет наибольшим в том абстрактном случае, когда к(,< (<] = 0 и будет опреде- ляться согласно выражению: 4Q% = (1- l^)*100. \ -J ^ эксп I Результаты расчетов по (9) показывают, что формула (8) хорошо соответствует опытный данным, приводя к среднеквадратичным отклонениям расхода системы галерея - ко Ж KB C. KB. Формула (8) дает реальные результаты на границах. При ц ^ 1, 1’затв ^ 1,68,что равно опытному значению этого коэффициента при ц = 1. При ц ^ 0, Гзатв ^ ю, что вполне соответствует природе этого коэффициента, раскрываемого выражением (3), согласно которому при ц ^ 0 отношение w0/wc ^ от. Это вызвано тем, что в технических условиях и нормах за расчетную формулу для ко- нусный затвор всегда меньшим, чем ±3,2%, т. е.: < ±3,2%. Следует отметить, что формула (8) дает результаты, близкие к данным, приведенным в своде правил [1] для конусных затворов с параметрами а = 50°, daбс/d0 = 1,1, dmax/d0 = 0,68. При сравнении следует учесть, что коэффициенты потерь, приведенные в [1] на единицу меньше коэффициента Гзатв, т. е.: ^ГУ = ^ затв — 1. (10) эффициента расхода системы принято вместо (10) выражение: Мсист 1 + а0 + ^х/. Сравнивая (11) о (5),и учитывая, что ас = 1, придём к (10). Выводы На основания экспериментального исследования для определения коэффициента t. Jtmg конусных затворов и других подобных затворов других фирм рекомендуются сравнительная таблица 1 и формула (8). Результаты исследования подтверждают и дополняют рекомендации свода правил [1].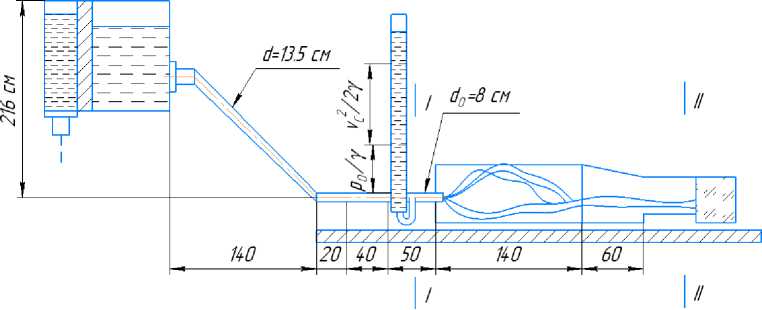
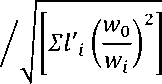
Список литературы Пропускная способность конусных затворов
- СП 290.1325800.2016. Водопропускные гидротехнические сооружения (водосбросные, водоспускные и водовыпускные). правила проектирования.
- Подрубалов М.В. Методы оценки статистических характеристик случайных процессов / М.В. Подрубалов, Д.В. Тулузаков // В книге: Ежегодная национальная научно-техническая конференция профессорско-преподавательского состава, аспирантов и студентов Мытищинского филиала МГТУ им. Н.Э. Баумана по итогам научно-исследовательских работ за 2020 г. Сборник тезисов докладов. - Красноярск, 2021. - С. 63-64. EDN: MUCCRS
- Podrubalov M. Researching rolling resistance of the wheeled forestry tractor at skidding / V. Klubnichkin, E. Klubnichkin, M. Podrubalov, V. Makarov // IOP Conference Series: Materials Science and Engineering. 108, Development, Research, Certification. Сер. "108th International Scientific and Technical Conference of the Association of Automotive Engineers "Intelligent Car Systems: Development, Research, Certification". - 2019. - С. 012003.
- Журавлева, Л.А. исследования параметров потока воды в трубопроводе широкозахватных дождевальных машин / Л.А. Журавлева // Аграрный научный журнал. - 2023. - № 1. - С. 136-143. EDN: UIPXRK
- Абдразаков Ф.К. Рациональное снижение металлоемкости при конструировании широкозахватных дождевальных машин / Ф.К. Абдразаков, Л.А. Журавлева, В.А. Соловьев // Аграрный научный журнал. - 2018. - № 5. - С. 37-41. EDN: XOUCGL
- Есин А.И. Исследования характеристик потока воды в водопроводящем поясе дождевальной машины / А. И. Есин, Д.А. Соловьев, Л.А. Журавлева // Научная жизнь. - 2018. - № 2. - С. 16-25. EDN: YVTTJU


