Простая аналитическая модель тепловых полей для разработки цифровых двойников процесса промышленной дуговой сварки

Сварка – надежный и эффективный способ соединения металлических изделий, который используется практически во всех отраслях промышленности. В связи с этим используемые технологии должны обеспечивать качество и экономичность производимых изделий. Однако практика показывает, что традиционные методы сварки не всегда обеспечивают выполнение этих требований [1]. Термический процесс, включающий интенсивный нагрев соединяемых частей изделия с помощью источника тепла, является определяющим при дуговой сварке. Он определяет протекание практически всех других сварочных процессов, в том числе форму ванны, создание металлургической связи, формирование металлоконструкций и остаточных напряжений (деформаций) в сварных соединениях и прилегающих к шву участках. Остаточные растягивающие напряжения, как правило, вредны, повышая восприимчивость сварного шва к усталостным повреждениям, коррозионному растрескиванию под напряжением и разрушению [2]. При оценке риска роста дефектов, например поверхностных дефектов трубопроводных систем, остаточные напряжения при сварке могут вносить больший вклад в общее поле напряжений, чем напряжения, вызванные расчетными нагрузками [2]. Кроме того, для предотвращения коррозионного растрескивания под напряжением в корневой зоне сварных швов из нержавеющей стали необходимо соблюдать определенные требования в отношении условий процесса, свойств материала и остаточных сварочных напряжений. Поэтому для достижения качества сварочного процесса необходимо моделировать совокупность термических, металлургических и механических процессов. Наиболее распространенным подходом к моделированию процесса сварки является использование численных методов, таких как метод конечных элементов (МКЭ), который обеспечивает хорошую точность результатов за счет уменьшения размеров элементов при увеличении их количества [3–5]. Однако трехмерная модель, позволяющая детально фиксировать распределение остаточных напряжений в процессе сварки, требует значительного времени расчета, поскольку механические явления при сварке представляют собой сильно нелинейные процессы. Это допустимо на этапе разработки сварочного процесса, но совершенно непригодно для создания цифрового двойника, используемого в режиме реального времени для контроля качества сварки, где время моделирования не может превышать нескольких секунд. В связи с этим в последнее время возник интерес к поиску упрощающих допущений с минимальными потерями в точности, обеспечивающих повышение

Мирзаев Д.А., Окишев К.Ю., Простая аналитическая модель тепловых полей для разработки Мирзоев А.А. цифровых двойников процесса промышленной дуговой сварки быстродействия всего комплексного подхода к моделированию процесса сварки. Наиболее часто используемой процедурой в рамках комплексного моделирования термических, металлургических и механических сварочных процессов является расчет температурного поля. Исследователи достигли значительного прогресса в аналитическом моделировании движущихся источников тепла и сварочных процессов, что представлено в литературе [6–10]. Тем не менее расчет теплового поля связан с численной оценкой достаточно сложных объемных интегралов, что замедляет моделирование. В работе [11] показано, что комплексное моделирование процесса сварки достаточно устойчиво к вариациям температурного поля, возникающим из-за различных допущений о форме и распределении начальной температуры источника дуги. Это обстоятельство побудило нас в данной статье предложить приближенное аналитическое выражение в элементарных функциях для тепловых полей. Это решение содержит всего два регулируемых параметра (эффективная ширина и температура электрода), которые можно подобрать для получения максимальной точности моделирования при заданной толщине и материале свариваемой трубы. Допускаемая при этом погрешность полностью компенсируется высокой скоростью расчета температурного поля.

1. Метод расчета процесса охлаждения сварных швов

Большая работа по расчету охлаждения сварных швов выполнена профессором

А.М. Попковым [12]. Мы усовершенствовали предложенный им метод, чтобы сделать модель более реалистичной.

Аналитическое моделирование нагрева и охлаждения при сварке в [12] основано на известном решении задачи нагрева пластины или трубы точечным источником тепла, быстро движущимся прямолинейно [13, 14].

т ( r ,T ) = T o +

qn 2nAvT

• exp

—

2 A r

4 ат _y

где q – тепловая мощность источника, η – эффективный КПД нагрева металла дугой (согласно [12] для сварки под флюсом η = 0,8–0,9; мы используем значение η = 0,85), ν – скорость источника тепла, τ – время (при τ = 0 источник пересекает условное начало координат, от которого отсчитывается радиус-вектор r в сечении, перпендикулярном траектории источника), a – температуропроводность, λ – теплопроводность (мы используем значения, характерные для трубных сталей a = 5,5·10^–6 м²/с, λ = 29 Вт/(м·К)).

Рассмотрим любую точку на расстоянии r от оси шва, расположенную на поверхности трубы. При τ = 0 начальная температура в этой точке будет T0, которую в статье мы будем принимать равной 22 °С. Затем температура будет повышаться, достигать максимума и снова падать. Мак- симальная температура достигается в момент r2

т =     ,

4a и принимает значение

T max = T o + 2^ ^ exP( — 1) . nAvir

Чем меньше r ², тем выше T _max. На некотором расстоянии r = δ температура станет равной температуре плавления T m ; тогда при меньших радиусах металл будет расплавлен. Полагая T max = T m , находим радиус жидкой зоны:

6 =

² aqn • exp^{( —} 1)

( nXv(T m — T o ) )

= 2,108 Л0 ^{— 4} •

qn

I v (T m — T o ) )

.

Для стенки толщиной 16–17 (в среднем 16,5) мм электрическая мощность дуги, используемой на ОАО «Челябинский трубопрокатный завод», составляет q = 163 кВт, а ее скорость v = 120 м/ч = 0,033 м/с. Учитывая, что коэффициент полезного действия η = 0,85 [12], а температура плавления стали T m = 1572 °С, получаем δ = 11,0 мм. Рассчитанная глубина расплавленной зоны (т. н. «ванны») в общем близка к реальной величине.

Оценим среднюю температуру расплавленной ванны:

Физика

1      r_

T = —• [ T ( r , т)nrdr = T nS 2/2 ^J_o                0

+ nS ²

qqa ^v

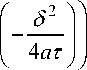
Но так как S ² = 4 ат , а в силу (3):

то

2 aqn nXvS ²

= exp(1) • (T„ - T o ) ,

T = T 0 + T - T o ) • ( exp(1) - 1 ) = 1,718T_m - 0,718 T .

Основным недостатком описанного метода является форма изотермы – полуокружность. Это означает, что если глубина расплавленной зоны равна S, то ширина шва равна 2S. В рассмотренном случае ширина шва должна быть равна 2 • 11,0 = 22,0 мм, тогда как на самом деле она со ставляет в среднем 30±3 мм. Предлагаемый нами метод позволяет устранить эту проблему, которая, очевидно, связана с пренебрежением реальным диаметром сварного электрода. Этот недостаток можно преодолеть, если моделировать электрод радиуса l при помощи двух источников тепла мощностью q/2, движущихся синхронно и параллельно друг другу на расстоянии 2l. Пусть начало координат O лежит ровно посередине (рис. 1).

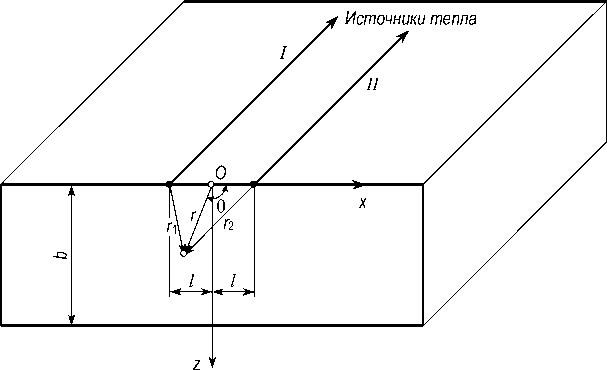
Рис. 1. Предлагаемый вариант замены одного источника тепла двумя источниками на расстоянии 2 l между ними

Если бы имелся один источник тепла мощностью q /2, то радиус ванны был бы

^S 1/2

= 2.108 •Ю^{- 4}

V 2 v(T m -Т 0 ) J

= 7,76 мм

Разумно принять 2 l = 13 мм, чтобы обеспечить требуемую ширину шва 2·7,76 + 13 = 28,5 мм.

Используя принцип аддитивности [13], запишем температурное поле вокруг двух линейных источников тепла:

Т ( r ,т ) = T +

qn

4nXvT

exp

—

v

4 ат

J

+ exp

—

v

r ₂

4 ат

J

где r1 и r2 – радиус-векторы точки, отсчитываемые от линий источников (см. рис. 1). Удобно ввести такую систему координат zOx, чтобы её начало располагалось симметрично относительно линий токов, и использовать полярные координаты 0 и r. Поскольку r12 = r2 +12 - 2rl cos(180° - 0) = r2 +l2 + 2rl cos 0,                      (9а)

r ₂ ² = r ² + 1 ² - 2 rl cos 0 ,                                      (96)

то

T ( r ,т ) = T 0 +

qn 4лXvт

• exp

r ² + 1

—

4 ат

I rl        /11         I     rl        n exp I ----cos0 1 + exp I--cos0

V 2 ат     J      V   2 ат

Изотермы превращаются в сложные кривые, которые, однако, можно легко построить численными расчётами. Но нас интересуют размеры оплавленной зоны прежде всего в горизонтальном и вертикальном направлениях. Вдоль оси z угол 0 = 90 ° и cos 0 = 0, поэтому

T ( r ,т ) = Т о +

qn 2nXvr

• exp

z + 1

4 ат _y

Проведя в (10) дифференцирование по 0, получим выражения, аналогичные (2) и (3), но с за меной r2 на z2 +12. Выражение (4) при z = 5 примет вид

( 5 ² + 1 2 ) 12

= 2,108 •Ю^{- 4} •

V V (^Т пл — T O ) )

= 11,0 мм,

откуда 5 = 711,0 2 - 6,5 2 = 8,9 мм.

Размер оплавленной зоны в горизонтальном направлении при 0 = 0 определяется удвоенной величиной радиуса r = x , при которой температура равна Т пл = 1572 °C. Для такого направления

Т ( x ,т ) = Т 0 +

qn

4nXvT

exp

( x -1 )² '

4 ат  _у

+ exp

( x + 1 )² ' 4 ат  _у

Однако, как показали оценки, вторая экспонента вблизи x ~ 14 мм имеет ничтожно малое значение по сравнению с первой, поэтому оказывается применимой формула (7), и расчётная ширина шва

2 x_nn = 2 5 _1/2 + 2 1 = 28,5 мм (14) оказывается равной действительному значению. Таким образом, модель двух линейных источников гораздо точнее описывает размеры и форму сварной ванны, чем модель одного источника [12].

Для практических целей важно знать распределение температуры и скоростей охлаждения вдоль оси z. Эту информацию можно получить, использовав выражение (11) и его производную по т. Но по мере увеличения координаты z и приближения к другой стороне пластины, где z = b (b – толщина трубы или пластины), мы сталкиваемся с другой проблемой. Формула (11) справедлива для полубесконечного вдоль z тела. Это означает, что при z = b температура будет убывать так, как если бы тепловой поток продолжал перемещаться вдоль z. Между тем, как показано в [12], теплообмен с окружающей средой на внешних поверхностях пренебрежимо мал, то есть противоположная поверхность является почти теплоизолированной. Ликвидировать этот недостаток метода можно следующим образом. Допустим, что мы увеличим в два раза толщину пластины, но с противоположной поверхности поместим дополнительно ещё два линейных источника тепла такой же мощности, расположив их точно под двумя первыми источниками. Все источники должны двигаться синхронно с одинаковой скоростью. Тепловые потоки от поверхностей z = 0 и z = 2b двигаются навстречу друг другу. На плоскости симметрии z = b потоки оказываются равными и противоположно направленными, так что на этой поверхности дТ)дz = 0, и по ток как бы отражается от этой поверхности. Область b < z < 2b является недействительной.

Вместо выражения (13) мы получим тогда более точное:

Т ( z ,т ) = Т ₀ + qⁿ 2 пЯvт

•

exp

22 z + 1

—

_V    4 ат

+ exp

Г   (2 b - z )² + 11

-

V

4 ат

которое позволяет найти распределение температуры вдоль оси z, являющейся осью симметрии сечения сварного шва. Изменение температуры в произвольной точке (r, 0) получается из выражения (10):

Т ( r ,т ) = Т +

4 плvт

•

exp

r ² + 1^г

—

_V   4 ат

+ exp

-

V

r ² cos² 0 + (2 b - r sin 0 )² + 1 ² 4 ат

х

Г r1               Г r1

exp I---- cos 0 1 + exp I-- cos 0

V 2 ат     )     V 2 ат

Физика

Для труб с толщиной стенки 30 мм нет необходимости использовать два точечных источника, так как глубина жидкой ванны б = 16,7 мм, рассчитанная по уравнению (5), примерно в 2

раза меньше ширины шва. В таком случае

T ( r ,т ) = Т о +

qn

2 Xvt

exp

(    2 Л

r

4 ат _;

⁺ exp

V

(2 b - r )² )

4 ат  _у

• 2.    Тестирование модели

• 3.    Результаты расчёта температурных полей при охлаждении сварных труб на воздухе

  Развитый выше метод моделирования тепловых полей был применен для расчетов термического цикла свариваемых труб при охлаждении на воздухе. При расчетах было использовано уравнение (15), а также следующие значения параметров: X = 29 Вт/(м²-К); а = 5,5•Ю ^{- 6} м²/с; v = 0,033 м/с (скорость движения трубы или электрода); 2 / = 13 •Ю ^{- 3} мм; n = 0,85; Т 0 = 22°C; Т пл = 1572 °C.

В экспериментальной работе [15] проводилось измерение температурного поля в толстом листе мягкой стали при сварке с использованием двухпроволочного электрода. Измеряющие термопары располагались на разной глубине заготовки по средней линии непосредственно под сварочной дугой, что соответствует формуле (11) нашей модели. Тогда сравнение результатов расчета с данными указанного эксперимента позволит получить представление о корректности модели. Для мягкой низкоуглеродистой стали характерные значения a = 6·10^–6 м²/с, λ = 60 Вт/(м·К). В табл. 1 приведены основные параметры нашей модели, соответствющие экспериментальной установке в работе [15], а также проведено сравнение экспериментальных и расчетных значений.

Таблица 1

Значения параметров в эксперименте [15] и сравнение полученных экспериментальных данных для максимальной температуры T ^max(z) и времени ее достижения t ^max на данной глубине z с расчетом по формуле (11)

Параметр глубина	l, мм	ν , см/мин	q , кВт	λ , Вт/(м·°С)	а, 10–6 м2/с	мах расчет	мах экспер.	t max , с расчет	t max, с экспер.
z = 5 мм	9	40	19,2	60	60	550	680	5	5
z = 7 мм						450	500	6	7
z = 9 мм						355	380	7	8

Видно, что согласие модели с данными эксперимента является вполне удовлетворительным.

• А) Охлаждение труб толщиной 12 мм

Электрическая мощность дуги при сварке труб толщиной b = 12 мм была принята равной q = 115 • 10³ Вт. Температурное поле в направлении толщины стенки, то есть радиуса трубы, было рассчитано для средней линии шва в определённых точках ( r = z ): z = 3; 6; 7,3; 9 и 11 мм. Точка z = 6 мм соответствует полутолщине, а точки z = 3 и 9 мм находятся на расстоянии 1/4 и 3/4 толщины от наружной поверхности. Рассматривается наружный шов.

Зависимость температуры в указанных точках от времени после прохождения дуги в данном сечении показаны на рис. 2. Они отражают термический цикл при сварке: нагрев, достижение максимальной температуры и охлаждение. Чем дальше от наружной поверхности расположена точка, тем ниже пик температуры и тем большее время необходимо для его достижения. С помощью кривых на рис. 2 можно легко оценить длительность кристаллизации, для чего следует провести горизонталь Т = Т пл = 1572 °C и найти её пересечения с кривыми термического цикла: первая точка пересечения есть начало, вторая - конец кристаллизации. В случае z 3 = 7,3 мм горизонталь T _пл касается максимума кривой; это означает, что эта точка является последней по глубине точкой оплавления, определяющей глубину жидкой ванны шва. Кристаллизация происходит примерно за 10 с.

Мирзаев Д.А., Окишев К.Ю., Простая аналитическая модель тепловых полей для разработки Мирзоев А.А. цифровых двойников процесса промышленной дуговой сварки

Очень интересным и важным является то обстоятельство, что после охлаждения длительностью 12 с температуры всех точек сварного шва оказываются очень близкими. Это означает, что вдоль средней линии шва температура почти постоянна: например, по прошествии 16 с она равна 1200 °C. Следовательно, металл внутреннего шва в этом месте нагревается выше температуры фазового перехода (A c3 ), и в стали возникает аустенит, который при дальнейшем охлаждении будет испытывать превращение. Увеличение длительности охлаждения, конечно, приводит к снижению температуры, но это снижение опять-таки оказывается почти одинаковым для всех точек средней линии шва.

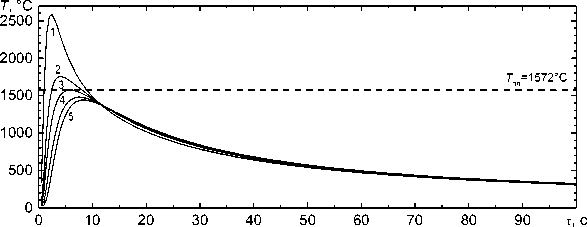
Рис. 2. Зависимость температуры в различных точках по толщине от времени после сварки для трубы толщиной 12 мм: 1 - z = 3 ; 2 - z = 6 ; 3 - z = 7,3 ; 4 - z = 9 ; 5 - z = 11 мм

На рис. 3 представлена зависимость скорости охлаждения у _охл = - dT(tt от времени. Самые большие скорости охлаждения наблюдаются при малых выдержках (менее 15 с), а затем они уменьшаются с течением времени, причём в разных точках средней линии сечения шва скорости охлаждения оказываются примерно одинаковыми.

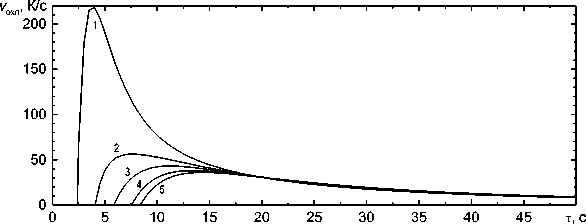
Рис. 3. Зависимость скоростей охлаждения для различных точек по сечению трубы толщиной 12 мм от времени охлаждения: 1 - z = 3 ; 2 - z = 6 ; 3 - z = 7,3 ; 4 - z = 9 ; 5 - z = 11 мм

На рис. 4 показано, как зависит скорость охлаждения в рассматриваемых точках от температуры, что очень важно для понимания характера превращения аустенита. Он может распадаться в интервале температур 800…500 °C на феррит и некоторое количество цементита в составе перлитной структуры, между 500 и 400 °C возможно превращение аустенита в бейнит, а ниже 400 °C возможна закалка, в ходе которой происходит образование высокопрочного мартенсита. У низкоуглеродистых трубных сталей, например 13ГС, для подавления реакции образования феррита нужны скорости охлаждения порядка 80 К/с, а для полной закалки – 150 К/с [4]. При охлаждении шва на воздухе в районе 600 °C скорость охлаждения составляет порядка 10 К/с (рис. 4; табл. 2), поэтому закалка невозможна.

Таблица 2

Зависимость скорости охлаждения сварного шва (К/с) от толщины трубы и температуры шва

Текущая температура, °C	Толщина трубы, мм
	12	16,5	30
650	12	8,4	3,6
500	7,0	4,9	2,2
400	4,4	3,1	1,4

Физика

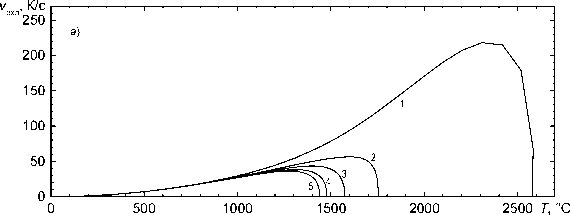
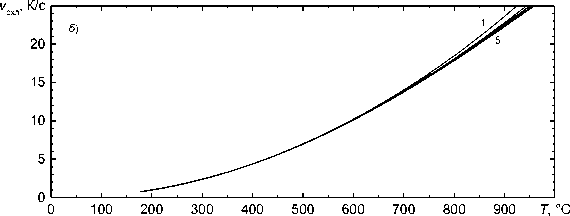
Рис. 4. Зависимость скорости охлаждения после сварки от температуры для различных точек по сечению трубы толщиной 12 мм:

1 - z = 3 ; 2 - z = 6 ; 3 - z = 7,3 ; 4 - z = 9 ; 5 - z = 11 мм;

а — во всей области температур; б — в области температур ниже 1000 °C

Б) Охлаждение труб толщиной 16,5 и 30 мм

Качественно соответствующие кривые изменения температуры для труб разной толщины оказываются сходными. Поэтому на рис. 5, 6 и 7 приведены кривые зависимости температуры и скорости охлаждения от времени, а также скорости охлаждения от температуры для труб толщиной 30 мм. Для труб толщиной 16,5 мм зависимости оказываются промежуточными между рис. 2, 3, 4 и рис. 5, 6 и 7. При расчётах принималось, что электрическая мощность дуги q = 163 - 10 3 Вт для толщины b = 16,5 мм и q = 378 - 10 3 Вт для толщины b = 30 мм.

Несмотря на качественное сходство, количественное различие между ними значительно. Например, при толщине 30 мм кристаллизация расплавленного металла на глубине 7,5 мм проходит за 30 с. Скорости охлаждения также существенно уменьшаются с увеличением толщины при фиксированной температуре и со снижением температуры при фиксированной толщине (см. табл. 2).

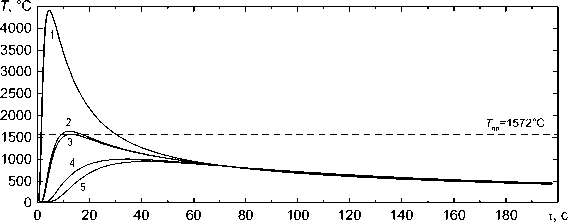
Рис. 5. Зависимость температуры в различных точках по толщине от времени после сварки для трубы толщиной 30 мм:

1 - z = 7,5 ; 2 - z = 15 ; 3 - z = 15,4 ; 4 - z = 22,5 ; 5 - z = 27 мм

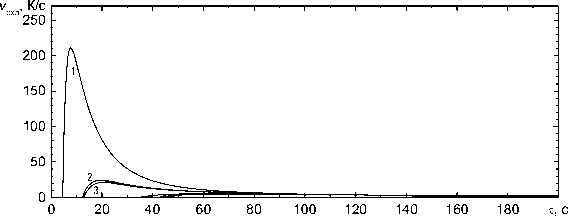
Рис. 6. Зависимость скоростей охлаждения для различных точек по сечению трубы толщиной 30 мм от времени охлаждения:

1 - z = 7,5 ; 2 - z = 15 ; 3 - z = 15,4 ; 4 - z = 22,5 ; 5 - z = 27 мм

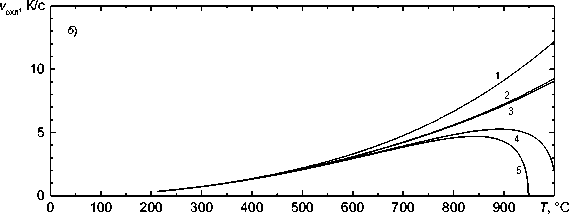
Рис. 7. Зависимость скорости охлаждения после сварки от температуры для различных точек по сечению трубы толщиной 30 мм:

1 - z = 7,5 ; 2 - z = 15 ; 3 - z = 15,4 ; 4 - z = 22,5 ; 5 - z = 27 мм;

а – во всей области температур; б – в области температур ниже 1000 °C

Заключение

Предложен достаточно точный аналитический метод моделирования тепловых полей в процессе технической сварки, учитывающий ряд реальных физических особенностей процесса, а именно конечный, а не точечный размер сварного электрода и ограниченную толщину свариваемого объекта. Этого удалось добиться путем использования модели с двумя точечными источниками тепла, разнесенными на величину порядка диаметра электрода. Показано, что новый расчетный метод гораздо лучше описывает температурное поле в области сварного шва, размер и форму сварочной ванны, чем модель одиночного источника [12]. Предлагаемая модель удовлетворяет как требованиям достоверности, так и вычислительной быстроты, необходимым для использовании в качестве элемента при разработке цифровых двойников процесса промышленной сварки. Показано, что использование данной аналитической модели позволяет легко проанализировать зависимость скорости охлаждения от температуры в различных точках стали вблизи трубных швов. Такая информация очень важна для понимания характера превращения аустенита и возможности закалки области сварного шва.

Финансирование

Исследование выполнено при финансовой поддержке Министерства науки и высшего образования Российской Федерации (государственное задание на выполнение фундаментальных научных исследований № FENU-2023-0011 (2023011ГЗ)).

Физика