Простой и универсальный метод принятия решений в пространстве критериев "стоимость-эффективность"

Понятийный аппарат, используемый в онтологии принятия оптимальных решений, непрерывно растёт. Это вызвано увеличением сложности решаемых практических задач и связанным с этим расширением фронта теоретических исследований. В дополнение к введённым нами в [1] и [2] понятиям расширенной Парето-оптимальности, прогрессивных решений, уровня прогрессивности решений и уверенных суждений лица, принимающего решение (ЛПР) в настоящей статье предлагается новое понятие шансов оптимальности многокритериальных альтернатив . Это понятие, по мнению автора, имеет прозрачный смысл, доступный пониманию ЛПР с любым уровнем математической подготовки. В то же время оно позволяет уверенно решать слабо формализованные задачи многокритериального выбора при полном отсутствии дополнительно вводимой информации. Понятие применимо в задачах любой размерности и степени неопределённости, однако в настоящей статье оно иллюстрируется на простой и потому наглядной задаче двухкритериального выбора, что позволяет показать его ценность.

1    Постановка задачи

Пусть задано m вариантов решений, характеризуемых количественными значениями двух критериев: стоимости и эффективности. Обозначим через i = 1,..., m номер варианта решения, а через ci, ei - значения для него количественных критериев стоимости и эффективности. Учитывая, что содержательный характер вариантов решения в данной постановке не имеет значения, будем для краткости называть вариантом решения вектор его критериев эффективности.

Поставим задачу разработать простой, универсальный, максимально обоснованный метод, который позволяет ЛПР, не привлекая никакой дополнительной информации, получить объективную скалярную количественную оценку степени оптимальности каждого варианта решения; при этом, при желании, ЛПР может уточнять постановку задачи своими «расплывчатыми» суждениями типа «лучше» или «важнее».

2    Описание метода

Благодаря простоте применения, предлагаемый метод может быть использован «вручную» любыми лицами, заинтересованными в объективной сравнительной оценке различных вариантов решений по критериям «стоимость–эффективность», даже если они владеют только элементарной математикой.

• 2.1    Выбор наилучшего из нескольких вариантов решения

Пусть требуется выбрать наилучшее решение из шести возможных решений, представленных в таблице 1. Содержательный смысл решений может быть любой (это различные проекты танков или варианты городов, в которых планируется провести отпуск и т.д.), существенны лишь две характеристики каждого решения, представленные во втором и третьем столбцах таблицы 1: стоимость (затраты на его реализацию) и эффект, который будет при этом получен.

Таблица 1 – Исходные данные примера

Вариант решения	Стоимость (у.е.)	Эффективность (у.е.)	Нормированная стоимость	Нормированный дефект (потери)
1	2	3	4	5
А	100	16	0	1
Б	165	20	0,65	0,6
В	120	17	0,2	0,9
Г	200	26	1	0
Д	175	23	0,75	0,3
Е	150	18	0,5	0,8
min	100	16	0	0
max	200	26	1	1

Сложность выбора наилучшего решения для заинтересованного в этом человека или организации (ЛПР) состоит в том, что не существует единственного «объективного» способа сравнения между собой двух вариантов решений, один из которых, например, по стоимости лучше, а по эффективности хуже другого. Таких способов, в одинаковой степени разумных, бесконечно много. Разные способы будут приводить к разным результатам выбора.

Идея предлагаемого нами метода состоит в том, чтобы перебрать (теоретически) все «разумные» способы сравнения, при каждом из них определить наилучшее решение и окончательно принять за наилучшее решение то, за которое «проголосует» большинство перебираемых способов. Реализовать эту идею удалось весьма простым алгоритмом, который изложим по шагам.

Шаг 1. Исключение заведомо неоптимальных вариантов решений. Проверим, что в таблицу 1 не включён ни один заведомо неоптимальный вариант решения, т.е. такой, который по обоим показателям уступает каким-либо другим вариантам решений из таблицы.

Шаг 2. Нормализация исходных данных. Найдём в каждом из столбцов 2 и 3 таблицы 1 наибольшее и наименьшее значения ( min и max ), а затем рассчитаем для каждого варианта решения две новые характеристики, по каждой из которых ЛПР стремится к минимуму : нормированную стоимость и нормированный дефект (потери), отражающие относительные значения стоимости и эффективности.

Нормированная стоимость i =

(стоимость i - минимальная стоимость) /

(максимальная стоимость – минимальная стоимость)

Нормированный дефект i =

1 - (эффективность i - минимальная эффективность) /

(максимальная эффективность – минимальная эффективность)

Результаты расчёта показаны в 4-м и 5-м столбцах таблицы 1.

Шаг 3. Расчёт индексов стоимости и дефекта. Построим таблицу 2, расположив в ней результаты расчётов в порядке возрастания нормированной стоимости и перенумеровав их в этом порядке (при этом значения нормированного дефекта автоматически расположатся в порядке убывания).

Таблица 2 – Нормализованные исходные данные и расчётные параметры примера

Номер варианта решения	Нормированная стоимость (с)	Нормированный дефект (d)	Индекс стоимости	Индекс дефекта 1/индекс стоимости	Интервалы индексов	Шанс оптимальности варианта решения
1	2	3	4	5	6	7
1 (А)	0	1	0,2	5	0,2	10
2 (В)	0,2	0,9	0,555	1,8	0,355	18
3 (Е)	0,5	0,8	0,812	1,231	0,257	13
4 (Б)	0,65	0,6	1,25	0,8	0,388	19
5 (Д)	0,75	0,3	3,333	0,3	0,5	25
6 (Г)	1	0		0	0,3	15

Полученная задача принятия решения показана на рисунке 1. По каждому из критериев ЛПР стремится к минимизации.

Заполним столбец с названием «Индекс стоимости». В первую его строчку занесем частное от деления нормированной стоимости варианта решения 2 на нормированные потери предшествующего варианта решения (с номером 1) и так далее вплоть до предпоследней клетки столбца, как показано линиями на таблице 2.

В ячейки столбца «Индекс дефекта» таблицы 2 внесем результаты деления единицы на числа, стоящие в тех же строках столбца «Индекс стоимости». В последнюю клетку столбца «Индекс дефекта» внесем нуль.

Шаг 4. Расчёт шансов оптимальности вариантов решений. Сначала заполним столбец 6 таблицы 2, для удобства прежде выделив в столбцах 4 и 5 числа, не большие единицы.

В первую строку столбца 6 занесем число из первой строки индекса стоимости. Затем, идя от первой строки столбца 6 вниз, будем вносить в очередную ячейку разность отмеченных подчеркиванием индексов стоимости, стоящих в текущей и последующей (с большим номером) клетках индекса стоимости (столбец 4). Так, во вторую строку занесем число 0,355 как разность между 0,555 и 0,2. Продолжаем этот процесс, пока не закончатся отмеченные подчёркиванием числа.

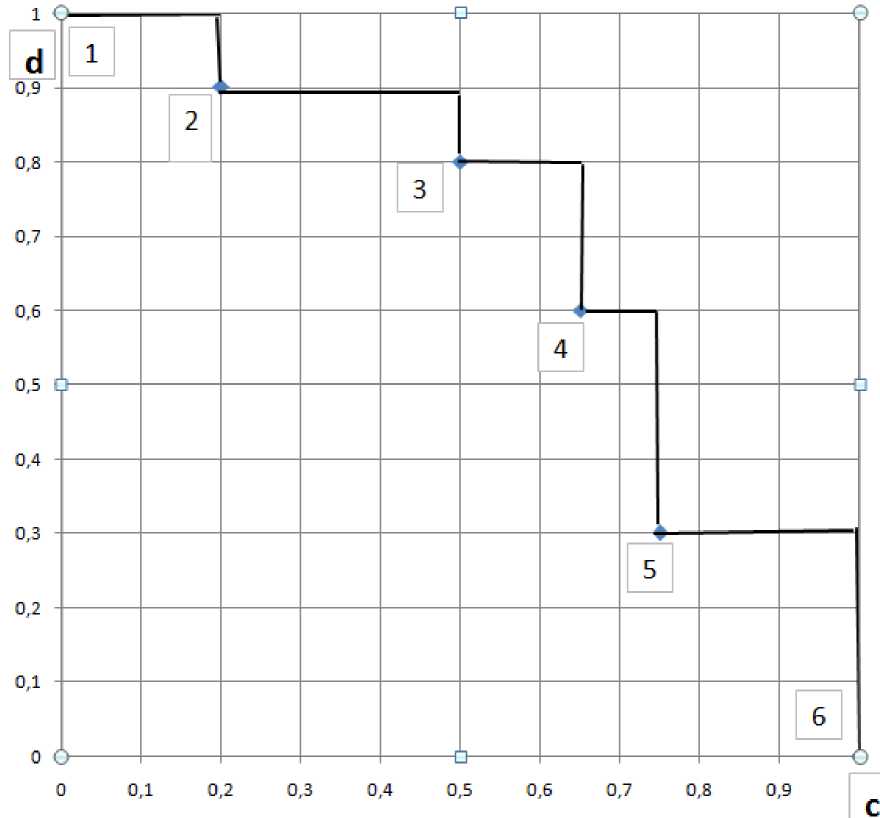
Рисунок 1 – Пример задачи выбора решений (варианты 1–6) в критериях «нормированная стоимость–нормированный дефект (эффективность)»

Аналогично, идя от последней строки столбца 6 вверх , будем вносить в очередную ячейку разность отмеченных подчеркиванием индексов дефекта, стоящих в предыдущей (с меньшим номером) и текущей ячейках индекса дефекта (столбец 5). Так, в последнюю строку занесём число 0,3 как разность между 0,3 и 0. Продолжаем этот процесс, пока не закончатся отмеченные подчёркиванием числа.

В редких случаях процесс завершится полным заполнением всех клеток столбца 6, тогда в ячейке, в которой «встретились» оба процесса заполнения (сверху и снизу), окажется единица. Как правило же, одна клетка окажется незаполненной. В нее нужно внести число, которое дополняет сумму всех чисел столбца 6 до числа 2. В нашем примере это число равно 2–0,2–0,355–0,257–0,5–0,3 = 0,388.

Теперь заполним последний столбец таблицы 2 (столбец 7), перенеся в него числа столбца 6, умноженные на 50 (рекомендуется округлить их до ближайших целых чисел так, чтобы сумма всех чисел в столбце 7 составила 100).

Числа, стоящие в столбце 7 таблицы 2, характеризуют целесообразность выбора соответствующих им решений в качестве оптимальных. В рассматриваемом примере, таким образом, наилучшим решением является решение 5 (Д).

• 2.2    Выбор наилучшего решения, когда один показатель «важнее» другого

• 2.3    Графическое решение

Возможно, ЛПР может с уверенностью уточнить свое понимание ситуации выбора, считая, что один из показателей «важнее» другого, например, стоимость решения для него имеет большее значение, чем эффективность (при этом не требуется пытаться определить, «насколько» важнее, это никогда невозможно с уверенностью сделать).

В этом случае в столбце «Интервалы индексов» следует оставить лишь те числа, которые получены в результате «регулярной вниз/вверх» работы с выделенными подчеркиванием числами в столбце индексов « важнейшего » показателя (поэтому, когда эффективность «важнее», подчёркнутое значение 0,8 в столбце «Индекс дефекта» не будет оставлено). Затем следует вычислить сумму этих чисел и записать разность единицы и этой суммы в ячейке, ближайшей к оставленным числам этого столбца. В остальные ячейки столбца вписать нули. Окончательно в столбец «Шанс оптимальности вариантов решений» вписать числа из столбца «Интервалы индексов», умноженные на 100. Как показано в таблицах 3 и 4, если стоимость важнее эффективности, наилучшим оказывается решение 2 (В), а если эффективность «важнее» стоимости – по-прежнему, решение 5 (Д), но шансы его признания оптимальным вдвое возрастает по сравнению со случаем, когда показатели представлялись ЛПР эквивалентными (50% против 25%).

Таблица 3 – Вычисление шансов оптимальности решений в примере, если стоимость «важнее» эффективности

Номер варианта решения	Интервалы индексов	Шанс оптимальности варианта решения
1 (А)	0,2	20
2 (В)	0,355	36
3 (Е)	0,257	26
4 (Б)	0,188	19
5 (Д)	0	0
6 (Г)	0	0

Таблица 4 – Вычисление шансов оптимальности решений в примере, если эффективность «важнее» стоимости

Номер варианта решения	Интервалы индексов	Шанс оптимальности варианта решения
1 (А)	0	0
2 (В)	0	0
3 (Е)	0	0
4 (Б)	0,2	20
5 (Д)	0,5	50
6 (Г)	0,3	30

Содержание описанного алгоритма удобно изобразить в графической форме, показанной на рисунке 2.

Построим квадрат ABCD со стороной, равной единице. Сторону BC назовем линией стоимости, а сторону DC – линией дефекта.

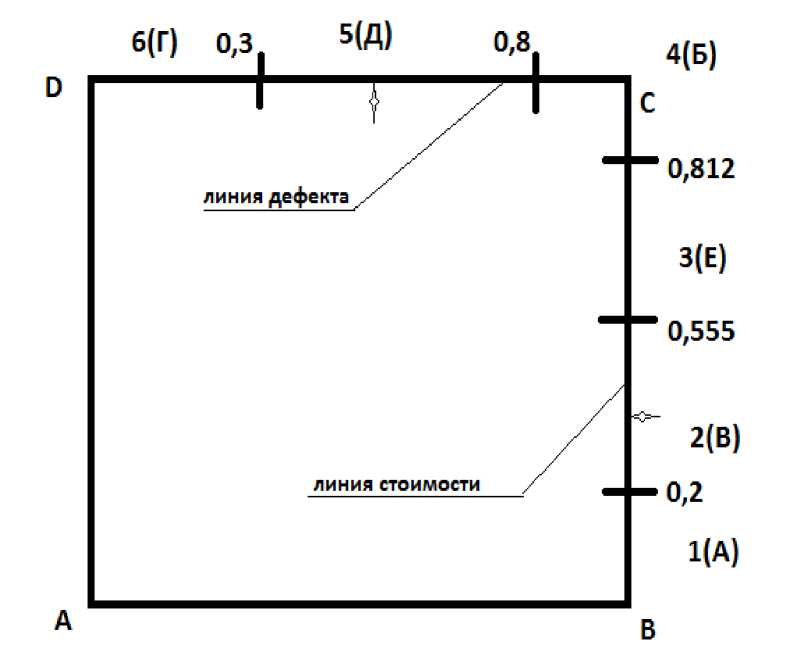
Рисунок 2 - Графический метод расчёта шансов оптимальности для вариантов решений

На линии стоимости, начиная от точки B , отложим значения индекса стоимости, выделенные подчеркиванием в столбце 4 таблицы 2. На линии дефекта, начиная от точки D , отложим значения индекса дефекта, выделенные подчеркиванием в столбце 5 таблицы 2. Пронумеруем получившиеся интервалы последовательно цифрами от 1 до 6 (очевидно, это номера сравниваемых решений), передвигаясь от точки B к точке D через точку С.

Если ЛПР не считает один из критериев более важным, чем другой, то длины пронумерованных интервалов, умноженные на 50, равны шансам соответствующих вариантов решений быть оптимальными.

Если же ЛПР считает, например, что критерий «стоимость» важнее критерия «эффективность», то линия менее важного критерия исключается из рассмотрения. Варианты решений, интервалы которых попадают на оставшуюся в рассмотрении линию, имеют шансы быть оптимальными. Эти шансы равны длинам интервалов, умноженным на 100.

В нашем примере, если стоимость «важнее» эффективности, то шансы быть оптимальным для варианта решения 1 (А) равны 20, для варианта 2 (В) равны 35,5, для варианта 3 (Е) равны 25,7 (т.е. вдвое больше, чем в случае равноважных критериев); шансы оптимальности варианта решения 4 (Б) равны 100 • (1 - 0,812) = 18,8. Варианты 5 (Д) и 6 (Г) вообще не могут быть признаны оптимальными.

Если же более «важным» признан критерий эффективности, то шансы оптимальности варианта решения 4 (Б) равны 100 • (1 - 0,8) = 20, варианта 5 (Д) - 50, варианта 6 (Г) - 30; нулевые шансы оптимальности у вариантов решений 1 (А), 2 (В), 3 (Е).

• 2.4    Выбор наилучшего решения, когда ЛПР может уверенно указать, что какой-то вариант решения для него лучше какого-то другого

Возможно, в некоторых случаях ЛПР может уменьшить неопределённость, имеющуюся в задаче принятия решений, указав два не обязательно реальных варианта решений, из которых, по его уверенному суждению, один заведомо лучше другого. Обозначим нормированные стоимость и дефект лучшего решения ( good) через c g и d g , а нормированные стоимость и дефект худшего решения ( bad) через c b и d b . Чтобы эта информация не была тривиальной или противоречивой соотношение значений показателей должно быть разнонаправленным, т.е., если c g >  c b , то d g <  d b (случай А ), а если c g <  c b , то d g >  d b (случай Б ) .

В случае А отложим на линии стоимости от вершины B отметку c b / d g , а на линии дефекта - от вершины D отметку d b / c g . Допустимыми следует считать точки этих линий, расположенные соответственно между этими отметками и углами квадрата соответственно B и D .

В случае Б отложим на линии стоимости от вершины B отметку c g / d b , а на линии дефекта - от вершины D отметку d g / c b . Допустимыми следует считать точки этих линий, расположенные соответственно между этими отметками и углами квадрата соответственно B и D . Если величина отметки равна или превышает единицу, допустимыми остаются все стороны квадрата ABCD (рисунок 2).

Например, пусть ЛПР уверенно считает, что вариант решения (0,3; 0,1) лучше, чем вариант решения (0,2; 0,9). Это соответствует случаю А , и на линии стоимости следует отложить отметку 0,3 / 0,9 = 0,333, а на линии дефекта - отметку 0,1 / 0,2 = 0,5. Длина интервалов, содержащих допустимые точки соответствующих им вариантов решения, составляет теперь: • для 1 (А) - 0,2;

• •    для 2 (В) -0,333 -0,2 = 0,133;

• •    для 6 (Г) - 0,3;

• •    для 5 (Д) - 0,5 - 0,3 = 0,2.

Разделив каждую длину на сумму этих длин и умножив на 100, получим шансы оптимальности соответствующих вариантов решений:

• •    для 1 (А) - 24,

• •    для 2 (В) -16,

• •    для 6 (Г) - 36,

• •    для 5 (Д) - 24.

Шансы оптимальности других вариантов решений равны нулю.

В итоге приводим сводную таблицу 5, отражающую изменение шансов оптимальности различных вариантов решений в зависимости от различных суждений ЛПР.

Таблица 5 - Сводная таблица расчётов шансов оптимальности при различных уверенных суждениях ЛПР

Вариант решения	Стоимость (у.е.)	Эффективность (у.е.)	Эквивалентная значимость критериев	Стоимость «важнее» эффективности	Эффективность «важнее» стоимости	(0,3;0,1) лучше, чем (0,2; 0,9)
1	2	3	4	5	6	7
А (1)	100	16	10	20	0	24
Б (4)	165	20	19	19	20
В (2)	120	17	18	36	0	16
Г (6)	200	26	15	0	30	36
Д (5)	175	23	25	0	50	24
Е (3)	150	18	13	26	0

3    Обоснование метода 3.1    Оценочная функция

Не уменьшая общности, будем считать, что среди вариантов решений нет неэффективных по Парето, и что номера вариантов решений следуют в порядке возрастания их стоимости. Нормируем значения критериев от минимального, принятого за нуль, до максимального, принятого за единицу, и перейдем от нормированной эффективности к нормированному дефекту d , дополняющему нормированную эффективность до единицы.

Тогда

• (1)          c i >  c i -1 , i = 2,..., m , с 1 = 0, C m = 1; d i <  d i -1 , i = 2,..., m , d 1 = 1, d m = 0.

Примем следующую гипотезу о принципиальном существовании оценочной функции .

Положим, что теоретически может существовать неизвестная оценочная функция, аргументами которой являются нормированные частные критерии. Она позволяет по значениям стоимости и эффективности любого варианта решения найти некоторую его скалярную оценку. Такая функция позволила бы легко решить проблему принятия многокритериального решения - лучшим был бы тот вариант решения, который имел бы наибольшее (наименьшее) значение такой оценки. Большинство существующих методов принятия многокритериальных решений направлено именно на отыскание такой функции. При этом её структура задаётся универсальной, а задача ЛПР сводится к тому, чтобы определить значение настроечных параметров этой функции, наиболее адекватных специфике конкретной решаемой задачи.

Часто в качестве оценочной функции используют линейную свёртку критериев. При этом настроечными параметрами являются коэффициенты, с которыми критерии входят в эту свёртку. Если используются нормированные значения критериев, то настроечные «весовые коэффициенты» отражают как бы сравнительную важность различных критериев с позиций ЛПР. Такая простая интерпретация привлекает пользователей, хотя показано (например, [7]), что подобная структура может «не замечать» даже некоторые Парето-оптимальные решения.

Предъявим к оценочной функции следующие требования:

• 1)    она должна иметь универсальную структуру, т.е. описываться универсальными математическими средствами, а для отражения специфики решаемой задачи включать лишь один свободный числовой параметр;

• 2)    она должна быть непрерывна и определена на квадрате [0, 1] х [0, 1];

• 3)    функция должна быть монотонна по своим аргументам, т.е. б о льшим значениям пар аргументов должно отвечать б о льшее (точнее, не меньшее) значение функции;

• 4)    любая Парето-оптимальная точка любой совокупности Парето-оптимальных точек на этом квадрате может рассматриваться как точка минимума этой функции при некотором значении параметра.

Покажем, что такая оценочная функция может иметь один-единственный вид (свёртка Гермейера [3]):

• (2)                 F = max ( x c • c , x d • d ), где max ( x c , x d ) = 1, x c >  0, x d >  0.

В соотношении (2) присутствуют два параметра x c , и x d , однако они функционально связаны и потому эквиваленты одному свободному параметру.

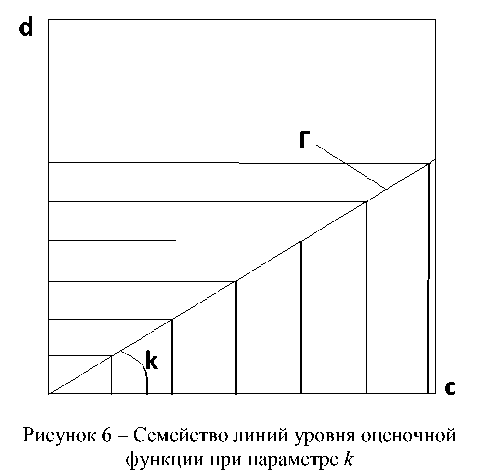
Действительно, рассмотрим, какой вид должны иметь семейства линий уровня оценочной функции. При любом значении входящего в функцию параметра её линии уровня должны заполнять весь квадрат [0, 1] х [0, 1], не пересекаться, являться монотонно убывающими, а их пометки (значение функции на линии уровня) должны возрастать от начала координат к периферии квадрата (рисунок 3).

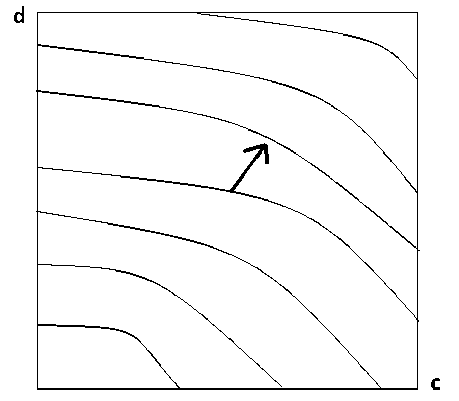
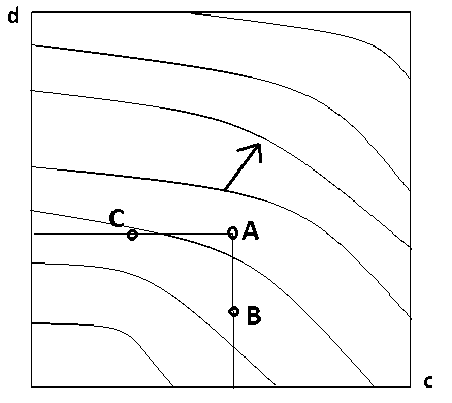
Рисунок 3 - Семейство линий уровня оценочной       Рисунок 4 - Система трех Парето-оптимальных функции при некотором значении параметра                           точек

Рассмотрим на квадрате [0,1] х [0, 1] множество, состоящее из трёх Парето-оптимальных точек A, B и C, построенное следующим образом: А - любая точка квадрата, В и С - также две любые точки, из которых первая имеет значение абсциссы, на бесконечно малую величину большее, чем значение абсциссы точки А, а вторая - значение ординаты, на бесконечно малую величину большее, чем значение ординаты точки А. Значения же соответственно ординат и абсцисс точек В и С меньше соответствующих координат точки А на конечную величину. Рисунок 4 иллюстрирует ситуацию, когда наименьшее значение оценочная функция принимает в точке В, поэтому при значении параметра, отвечающем изображенному на это м р юунке семейству линий уровня, эта точка определяется как Парето-оптимальная во множестве точек А, В и С. Легко представить себе, причём различным образом, семейство линий уровня, при котором линия с меньшей пометкой проходит через точку С, определяя её в качестве Парето-оптимальной. А вот линия уровня, определяющая в качестве Парето-оптимальной точку А, и потому имеющая пометку не больше пометок линий уровня, проходящих через точки В и С, может выглядеть лишь единственным образом, как показано на рисунке 5 (линия Г1). Действительно, при ином виде этой линии уровня, например Г2, через точки С (например, линия Г3) и В будут проходить линии уровня с меньшими пометками, чем пометка линии Г1.

Поскольку все три точки А, В и С являются текущими, отсюда следует, что семейство линий уровня оценочной функции при любом значении параметра должно иметь структуру, показанную на рисунке 6. А такой структурой обладает свёртка Гермейера (2). Параметром семейства линий уровня является коэффициент наклона k направляющей прямой Г . На этой прямой

Х с - с , = X d - d , или

• (3)                                       d / c = x_c / x_d .

Отметим, что аналогичные соображения относительно оценочной функции имеют место и в общей задаче принятия решений при любом конечном числе критериев f , j = 1,..., p :

• (4)            F = max j = i,_, _p ( X - f^j ), где max j = i,_, p ( X) = 1, X >  0, j = 1,..., p .

  

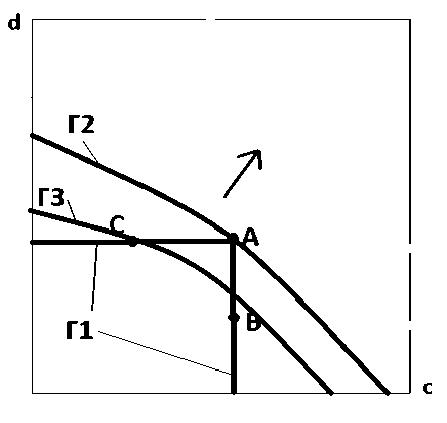
  Рисунок 5 - Иллюстрация особенности линии уровня Г1

  
  
  
  
  

• 3.2    Основные соотношения

Принятая гипотеза о принципиальном существовании оценочной функции делает задачу принятия многокритериальных решений математически замкнутой. Расплывчатое понимание необходимости сопоставления в ней «сравнительного влияния» различных разнокачественных критериев (в рамках настоящей статьи это стоимость и эффективность) на выбор «наилучшего решения» отображается введением в рассмотрение неопределённых коэффициентов x c , x d , удовлетворяющих наложенным в (2) ограничениям. Эти коэффициенты определяют наклон направляющей прямой Г (рисунок 6).

Если взглянуть на поставленную таким образом задачу принятия решения, то традиционный подход заключается в том, чтобы выявить конкретное значение этих коэффициентов, которое адекватно конкретно решаемой задаче. Мы считаем такой подход неверным теоретически и вредным практически, поскольку:

• ■    во-первых, объективно невозможно формализовать специфику конкретной задачи в виде единственного числа (в случае двухкритериальной задачи) или p - 1 чисел в случае использования p частных критериев;

• ■    во-вторых, стремление выявить это несуществующее число с помощью экспертных процедур или хитрых опросных процедур неоправданно усложняет и затягивает процесс принятия решения, а, кроме того, может подменять действительное понимание конкретики задачи ЛПРом, уполномоченным на это своим статусом, мнением определённых лоббистских групп.

Возможность внесения в решаемую задачу дополнительной информации, безусловно, должна быть сохранена, однако она должна сводиться к внесению органичных для ЛПР расплывчатых суждений типа «лучше-хуже», «более важно-менее важно», причем она не должна быть направлена на выявление, в конечном счете, конкретного значения параметра (набора параметров при более чем двух критериях) оценочной функции.

В [1] нами был обоснован учитывающий сказанное Метод уверенных суждений ЛПР (метод МУС), дающий простой, универсальный, максимально объективный, наиболее экономный и понятный для ЛПР способ решения задачи наилучшего выбора. Он состоит в том, чтобы в качестве комплексной оценки варианта решения рассматривать шансы его опти- мальности - меру множества допустимых значений параметра оценочной функции, при которых эта функция принимает на нём оптимальное значение по сравнению со значениями на всех других допустимых варианта решения. В [2] разработан метод определения шансов оптимальности вариантов решений в общей задаче многокритериальной оптимизации. В задаче, рассматриваемой в данной статье, учитывая наличие в ней всего двух критериев, этот метод принимает наиболее простой и наглядный вид. На рисунке 7 показаны точки, отображающие m вариантов решений, пронумерованных от 1 до m. Проведенные на рисунке прямые ограничивают наклон направляющих линий оценочной функции, между которыми решения оказываются оптимальными.

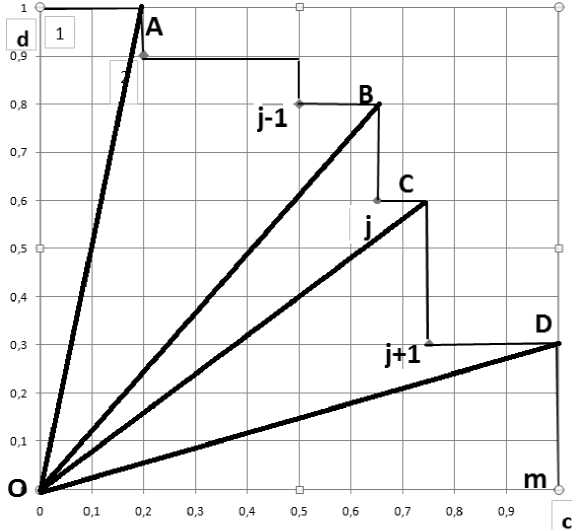
Рисунок 7 - Направляющие линии оценочной функции при расчёте шансов оптимальности вариантов решений

Для «внутреннего» варианта решения с номером j , j = 1,..., m наклон направляющих прямых ограничен линиями ОС , ОВ .

Это выразится неравенством

• (5)                                d i / c i ₊ 1 <  d / c = x_c / x d <  d i . 1 / c i

С учётом ограничений, наложенных в (2) на коэффициенты оценочной функции, неравенство (5) распадется на два неравенства:

• •    если x_c = 1, то d i / c i _{+ 1} <  1 / x d <  d i . 1 / c i , откуда c i / d i . 1 <  x d <  c i _{+ 1} / d i ;

• •    если x_d = 1, то d i / c i ₊ 1 <  x_c <  d i . 1 / c i .

Для оптимальности варианта решения с номером 1 направляющая прямая Г должна находиться между прямой ОА и осью ординат на рисунке 7. Аналогично рассуждениям, проведенным для «внутреннего» варианта решения, легко показать, что этому отвечают условия

X c = 1, 0 <  X d <  c 2 .

Заметим, что в данном случае неравенство (5) в предположении x_d = 1 приводит к условию x_c >  1 / c 2 , что возможно лишь в вырожденном случае c ₂ = 1.

Для оптимальности варианта решения с номером m направляющая прямая Г должна находиться между прямой OD и осью абсцисс на рисунке 7. Аналогично предыдущим рассуждениям, легко показать, что этому отвечают условия xd 1, 0 — xc — dm - 1 •

Соотношения, полученные в настоящем пункте, обосновывают все результаты, приведенные в разделе 2 статьи.

4    Выбор наилучшего из трёх решений

Особенно простые результаты в виде конечных формул получаются в задаче, в которой сравниваются всего три варианта решения. Как легко видеть из подраздела 3.2, в этом случае шансы оптимальности решений таковы:

Для решения, отображенного точкой 1, F 1 = c 2 /2, для решения, отвечающего точке 2, F г = 1 - ( c ₂ + d ₂ ) /2, а для решения, отвечающего точке 3, F ₃ = d ₂ / 2.

На рисунке 8 показаны зоны оптимальности каждого из трех вариантов решений. Его нужно понимать следующим образом. Если точка 2 расположена в некоторой точке изображенного на рисунке квадрата, то зона, в которую эта точка попала, показывает, какое из трёх решений будет иметь наибольшее значение шанса оптимальности. Рисунок полезен тем, что показывает, насколько должно отличаться от аналогов (точек 1 и 3) решение (точка 2), для того, чтобы оно было конкурентоспособно по сравнению с ними.

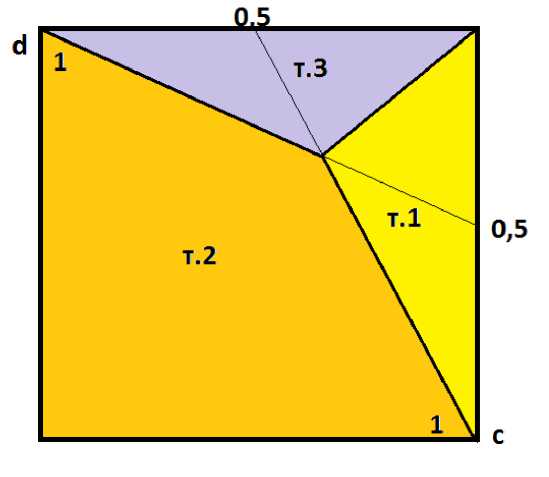
Рисунок 8 - Зоны оптимальности трёх вариантов решений

Заключение

Задаче выбора многокритериальных альтернатив присуща органическая неопределённость. Плодотворный путь в решении таких задач состоит не в том, чтобы пытаться получить от ЛПР в принципе неформализуемую дополнительную информацию о конкретной задаче, якобы устраняющую эту неопределённость, а в том, чтобы признать её органический характер и перейти к расчёту шансов каждого варианта решения оказаться оптимальным с учётом всего множества неопределённостей. Этот путь, реализация которого была начата нами сорок лет назад [4] и продолжена разработкой метода ПРИНН [5-7], продемонстрировал свои широкие возможности, предложив простое, универсальное и максимально объективное решение задачи выбора решений в критериальном пространстве «стоимость-эффективность».