Пространственная селективность четырехволнового преобразователя излучения с учетом термодиффузионного и электрострикционного механизмов нелинейности

Многокомпонентные среды, в которых, как правило, одновременно реализуется несколько механизмов нелинейности (тепловой, концентрационный, электрострикционный и т. д.), традиционно используются для получения с помощью четырехволнового преобразования волны с обращенным волновым фронтом в реальном масштабе времени [1–3]. Четырехволновой преобразователь излучения осуществляет преобразование комплексной амплитуды падающей на него волны с определенной точностью, которая и определяет качество восстановления волнового фронта в оптической системе: неоднородная среда – четырехволновой преобразователь – неоднородная среда [4–5].

С использованием метода функции размытия точки достаточно подробно проанализировано качество обращения волнового фронта при четырехволновом взаимодействии в средах с керровской, тепловой, резонансной нелинейностями с учетом структуры волн накачки, коэффициента отражения, углового и частотного сдвига [6–7].

Представляет практический интерес анализ пространственной селективности четырехволнового преобразователя в многокомпонентной среде с учетом как термодиффузионного, так и электрострикционного механизмов нелинейности.

1. Вывод выражений, описывающих пространственную селективность четырехволнового преобразователя излучения

Рассмотрим плоский слой нелинейной среды толщиной / , в котором распространяются две

волны накачки с комплексными амплитудами A ₁ и A ₂, сигнальная волна – с амплитудой A ₃. В результате вырожденного четырехволнового взаимодействия to + to - to = to генерируется объектная волна с комплексной амплитудой A ₄.

Исходное скалярное волновое уравнение, описывающее четырехволновое взаимодействие в нелинейной среде, есть

—2  7 2   2k dn

V² + k ² +--—

х

n ₀ dT

. Г da "1) 5T-2ik a + dC5C

-17

х

х ( a + A * ) — 0.

Здесь A = E A j , 5 T и 5 C — изменения температуры и концентрации; а — коэффициент поглощения; k – волновое число; n ₀ – среднее значение

показателя преломления.

Уравнение (1) дополняется системой балансных (материальных) уравнений для концентрации и температуры [8]:

~ д5 T c р = -divJ + 2аI, p д t             1        ’ д5 с

---— — div ( J + J^ д t           х 2 3

) ,

где

J 1 = - О ц grad 5 T - D 12 grad 5 C ,

J 2 = - D 21 grad 5 T - D 22 grad 5 C,                (3)

J 3 = -YgradI .

Здесь I = AA *; D^ — коэффициент теплопроводности; D ₂₂ – коэффициент диффузии; D ₁₂ – коэффициент термодиффузии; D ₂₁ – коэффициент, описывающий эффект Дюфура; у — коэффициент электрострикции; c _p – теплоемкость; р — плотность вещества. Уравнения (2)—(3) описывают среду с термодиффузионной и электро-

С учетом изменения интенсивности волн в не-

линейной среде волновое уравнение (1) примет

вид

Г            «1.2

V² + к ² + 2 k --(5 Т _о +5 Т ₃ J

I             n _о dT^ ^о

- 2 ik

d а

а +--

dC

( 5 С о +5 С 31 )

Z ^Aj = ^о .

j = 1

стрикционной нелинейностями.

Для установившегося режима

55 Т    д5С

----- = о,---- д t       д t

Пусть волны накачки плоские:

A1,2 (r) = A1,2 (z)exP (-ik1,2r), где /q 2 — волновые векторы волн накачки; r (ж, y, z ) — радиус-вектор.

Сигнальную и объектную волны разложим по

плоским волнам:

подставив (3) в (2), получим

D 11 V 2 5 Т + D ₁₂V²5 С = -2а I , D ₂₁V²5 Т + D ₂₂V²5 С + yV² I = 0.

ю

A j ( r ) = J A j ( к j , z ) exp ( - i К j P - ik jz z ) d к j ,

-ю

j = 3,4.

Из системы уравнений (4) получим однотип ные уравнения для 5T и 5C вида

DV25Т = -2аI + D2 V21,(5)

1                   D22

D2V25С =-2аI + 1D2 V21,(6)

• 2                  D21

где

D 12

D1 = D11 - D21

D 22

D2 = D12 - D22.

D 21

Будем рассматривать четырехволновое взаимодействие при следующих условиях:

• 1)    справедливо приближение заданного поля по волнам накачки | A 1 2]>> | A 3 4 1;

• 2)    коэффициент отражения мал A 4] <<  A 3I;

• 3)    учитывается решетка, возникающая при интерференции первой волны накачки и сигнальной волны.

Интенсивность излучения, распространяющегося в нелинейной среде, можно записать следующим образом:

I = I о + A i A 3 + A ? A 3 .

Здесь I о = A i A ? + A 2 A 2 * .

Тогда изменения температуры и концентрации можно представить в виде суммы быстро (5 T 31 , 5 C 31 ) и медленно (5 Т о , 5 С о ) меняющихся в зависимости от координат составляющих:

5 Т = 5 Т о +5 Т 31 +5 Т ? 1 ,

5 С = 5 С _о + 5 С ₃₁ + 5 С 31 .

Быстро меняющиеся составляющие температу- ры и концентрации разложим по гармоническим решеткам:

ю

5 T 31 ( r ) = J

5 T 31 ( к т , z ) exp ( - i к т p ) d к t ,

-ю

ю

5 С 31 ( r ) = J

5 < С 31 ( к с , z ) exp ( - i к С P ) d к С .

-ю

Здесь A _j – пространственный спектр j -й волны; p ( ж , y ) — поперечная составляющая радиус-вектора; 5 C T 31 и 5( С 31 — пространственные спектры тепловой и концентрационной решеток; к j — поперечные составляющие волновых векторов k _j ; к т и к с — волновые векторы тепловой и концентрационной решеток.

С учетом приближения медленно меняющихся амплитуд уравнение (7) распадается на систе- му уравнений вида

^* dA+ dz " iz / n о dn 5 T dT 0 dа +5 Сл dC 0 + а ^A1 = о, ^* d^A 2 - dz ". k _г По dn ST dT 0 + d^ 8C dC 0 1 +а J Av 2 = о, dA1) 3+ dz ik L n о dn 5 To dT 0 + d^ 5 C dC 0 1 +а J A 3 = о, (8) dAV 4 -dz . k i L по dn 5 T dT 0 + d^ 5 C dC 0 1 +а J AA4 + + . k dn - i-- _ nо dT 5 ^^31 + dа,р " 5 Cq dC 31J A 2 х х exp [-i (k2z - k4z )z J = о.

Уравнения (8) записаны при условии, что

—*         —*         —*       —*        —*       —*

к C = К T = ^К 1 ^{- к} 3 = ^к 4 - ^к 2 .

Решение первых трех уравнений системы (8)

есть

« 1 = 2а -Y D ¹² ( в² - к Т )

D 22

^в = 2^а + i ^—z ^{- —}z ) ;

^A1 ( ^z ) = ^A 10 ^ex p [- P ( ^z ) ] ,

A 3 ( ^K 3 , ^z ) = A 30 ( ^K 3 ) exp ^[- P ( ^z ) ] ,

A 2 ( ^z ) = A 20 exp ^[- P ( ^£ ) ⁺ P ( ^z ) ] .

Здесь

^A 10 = ^A 1 ^{( z} = ^{0 )} ,

^K T = |^K t| ; ^K 3 = |^K3I

Уравнение (10) записано при условии

d а

а >> —

dC

5 C 0 .

A A 30 ^(K 3 ) = A A 3 ^(K 3 , ^z = ^{0 )} ,

С учетом неизменности температуры на гранях нелинейного слоя ( 5 Т ( z = 0 ) = 5 Т ( z = £ ) = 0 ) решение уравнения (10) есть

A 20 = A 2 ^{( z} = ^£ ) ,

⁵ ^ T 31 ^(к Т , ^z ) =

z

P ( Z ) = J i 0 ^L

k dn n0 dT

5 T ( z i ) +а + ^5 C

^а 1 " A 10 AA 30 ^(к 3 ) _x D 1 ( ^в 2 ^{- к} Т )

dz ₁ .

Сделаем замену

A 4 ( z ) = A 4 exp [ P ( z ) ] .

Тогда уравнение, описывающее изменение пространственного спектра объектной волны,

f 1

xi-;----;

[ sh к т £

[exp ( -в £ ) sh к tz -

^- sh ( ^K t ( ^{z - £} ) ) ] ^- exp ( ^{-в z} )

примет вид

•w d^A ‘ [ . k dn - d а - 1 4+ i       5 T^i +    5 Ct A20 x dz [ n0 dT 31 dC 31 ] x exp [-P (£)] exp [-i (—z - k4z )z] = 0.

Проводя аналогичные рассуждения, из уравнения (6) получим уравнение для пространственного спектра концентраций частиц

С учетом граничного условия

A 4 ( K 4 , z = £ ) = 0

пространственный спектр объектной волны на передней грани нелинейного слоя есть

Av 4 ( K 4 , z = 0 ) = - A 20 exp [- P ( £ ) ] x

J n dT 31V ’ dC 31V ’ x exp [-i (—2z - k 4z ) z ] dz.

f <72        )

-k C 5 C31 +

( dz ²      J

+ 0 2 .A ¹⁰ v i 3 0 ^(K 3 ) exp ( -в z ) = 0,

D ₂

где

0 2 = 2а -y D ¹¹ ( в² -k C ) к c =|K c| .

D 21

Для нахождения решения уравнения (12) будем использовать граничное условие отсутствия потока концентрации частиц через грани [9] не-

Пространственный спектр объектной волны полностью определяется пространственными спектрами тепловой решетки и решетки концентраций.

Для нахождения пространственного спектра тепловой решетки рассмотрим уравнение (5). Оно распадается на два уравнения:

линейного слоя

d 5 C 31	d 5 C 31		= 0 z = £
dz	z = 0	dz

С учетом граничного условия (13) решение уравнения (12) есть

⁵ C C 31 ( ^K C , ^z ) =

^а 2" A 10 " A 30 ^{( k} 3 ) _x ^D2 ( ^в 2 ^{- K} C )

V 2 5 T ₀

+ M = 0, D 1

f-L [к c sh к c £

[exp ( -в £ ) ch к c z -

f d

₄ dz ²

-

^*

^K T ^{5 T} 31 ⁺

^{- ch} ( ^K C ( ^{z - £} ) ) ] ⁺ exp ( ^{-в z} )

+ а1

^A 10 AA 30 ^{( k} 3 )

D 1

, exp (-вz)=0

где

Зная выражения для пространственных спектров тепловой и концентрационной решеток (11), (14), используя уравнение (9), найдем пространственный спектр объектной волны на передней грани нелинейного слоя:

A 4 ( ^к 4 , z - 0 ) ^- A 4 т 1 ( к, z ^- 0 ) + A 4 T 2 ( к, z + " A 4 С 1 ( ^к, z ^- 0 ) + " A 4 C 2 ( ^к, z ^- 0 ) .

-0 ) +

Здесь

Av 4 T 1 ( к, z - 0 ) - 2a A 4 t ( к, z - 0 ) ,

A 4 т 2 ( ^к, ^{z -} 0 ) ^- -YА² ( ^p2 - ^к 2 ) A 4 т ( ^к, ^{z -} 0 ) , D 22

A 4 С 1 ( к, z - 0 ) - 2a A 4 С ( к, z - 0 ) ,

A 4 C 2 ( ^к, z ^- 0 ) ^{- -}Y D ¹ ( ^p 2 ^{- к} 2 ) A 4 С ( ^к, z ^- 0 ) .

D ₂₁

*

A ( к, z - 0 ) - - ikdn A ¹⁰ A ²⁰ A ^{30 (} к ) x ⁴ T ⁽ ,      ) П 0 dT D 1 ( p²-к² )

exp [- P ( / ) ]

^x 2             2       { exp^{(- 2 a / )x}

I к² + ( k 2 _z - k 4 _z ) I sk к /

x[к ch к / + i ( k 2 _z - k 4 _z ) sh к / ] - к exp ( -p / )

-

-к exp ( - i ( k 2 z - k 4 z ) / ) - i ( k 2 z - k 4 z ) sh к / + + к ch к / + ( 2a ) ¹ [к² + ( k _{2 z} - k _{4 z} ) ² ] x x sh к / [exp ( -2a / ) - 1] } ,

2      - d ^{a P} "A ¹⁰ A 20" A 30 ^(к) x

A4С (к,z - 0)-                      x dC D2 (p2 -к2 )

•w

A 4 C 1 ^-

•w

^A 4 c 2 ^-

x

exp [- P ( / ) ]

^[к 2 ^{+ ( k}2 z ^{- k} 4 z ) ]

{ exp ( -2a / ) x к sh к /

-

-

^k 4 z ) ^exp ( ^- i ( ^k 2 z ^{- k} 4 z ) ^/ ) ⁺ к sh к / +

-

^k 4 z ) 2 ]^x

к 2

2 k

-

.

трострикционной нелинейностей определяется выражениями вида

^ 1 -	А 4 т 1	D 22
	A 4 ' T 2	2ay D 12

	^A 4 С 1	D 21
^ 2	•V
	^A 4 С 2	2aY D 11

Меняя параметры нелинейной среды, можно изменять относительный вклад в объектную волну волн, связанных с термодиффузионной и электрострикционной нелинейностями.

На рисунке для сигнальной волны от точечного источника, расположенного на передней грани нелинейного слоя (AAЗ0 (к)- 1)^ приведены характерные графики зависимости от нормированной пространственной частоты к' - ^]//2k модулей нормированных спектров объектных волн:

^A 4 T 1 D 1         | i k dn

2a^ 4 -10^ A 20 exp [- P ( / ) ] ( n dT

2 A 4 т 2 D 22 D 1        J • k dn

Y D 12 A 10 A 20 exp ^{[- P} ( ^/ ) ]l ⁿ 0 ^dT

A 4 C 1 D 2        J d a I^-1

2a iA₁₀ ^A 20 exp [^{- P} ( ^/ ) ]l ^dC J

_______ AA 4 C 2 D 21 D 2 _______ J ^{d a} 'J ¹ Y ^D 11 AA 10 AA 20 exp [^{- P} ( ^/ ) ] V ^dC J

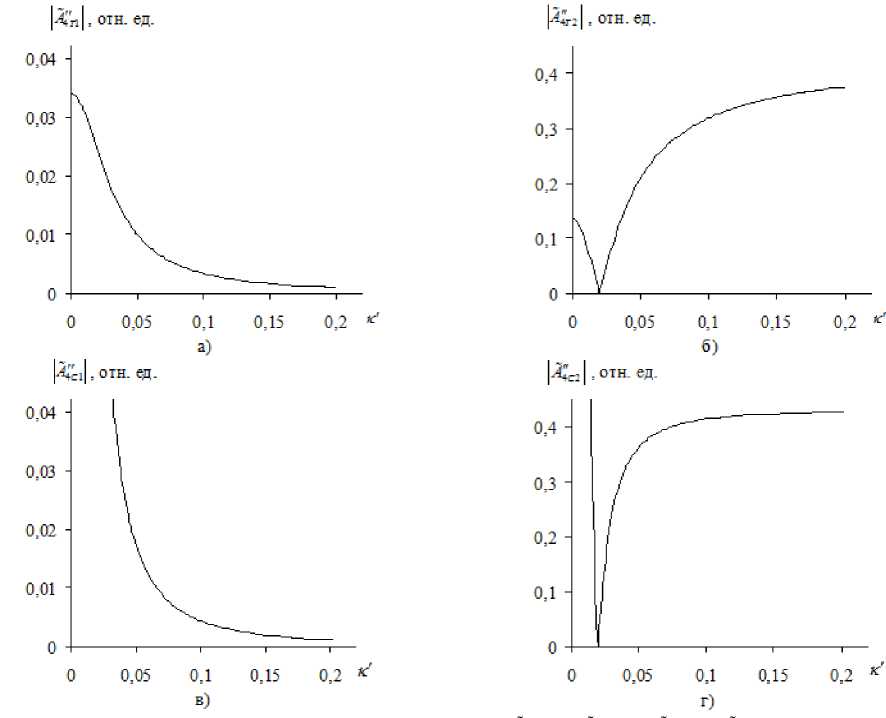
При наличии только термодиффузионной нелинейности (у - 0) модули спектров объектной волны с увеличением к' монотонно уменьшаются (рис., а, в). Ширина полосы пространственных частот волн, измеряемая по уровню 1 2 от максимального значения (для волны AA4T1) или по уровню пространственной частоты, в пределах которой сосредоточена основная энергия преобразованного изображения (для волны AA4С1) [10], определяет пространственную селективность четырехволнового преобразователя излучения.

Учет электрострикционной нелинейности при- водит к возникновению в среде двух дополнительных динамических (тепловой и концентрационной) решеток и, как следствие, двух дополнительных объектных волн AA4т2 и AA4с2. На малых пространственных частотах фазы этих дополнительных волн сдвинуты по отношению к фазам волн AA4T1 и AA4С1 на п, поэтому их наличие ослабляет суммарную объектную волну. Существует пространственная частота, определяемая в основном коэффициентом поглощения к ® 2a, при которой коэффициент отражения объектных волн, связанных с наличием электрострик-ционной нелинейности, равен нулю. На больших пространственных частотах к > 2a наличие дополнительных волн, связанных с электрострик-

Рис. Зависимости модулей нормированных амплитуд объектных волн A 4 т 1 ( а ), A 4 т 2 ( б ), A 4 с 1 ( в ), A 4с 2 ( г ) от пространственной частоты при 2к / = 10 4 , а / = 1

ционной нелинейностью, усиливает суммарную объектную волну. В предельном случае к ^ » значение модулей амплитуд волн A 4 т 2 и A 4 с 2 определяется величиной [1 - exp ( -2а / ) ] ( 2а / ) ¹.

Фазы объектных волн в параксиальной области ( к/ к <<  1 ) в зависимости от пространственной частоты меняются незначительно.

Характер зависимости амплитуд объектных волн, связанных с наличием электрострикцион-ной нелинейности (рис., б , г ), можно представить в виде суммы зависимостей:

A 4 T 2 = ^{[ 1} - ^exp ( ^{- 2 а /} ) ] ( ^{2 а /} ) ^{- f}T ( ^к ) ,

A 4 C 2 = ^{[ 1} - ^exp ( ^{- 2 а /} ) ] ( ^{2 а /} ) - f c ( ^к ) .

Здесь fT (к) и fc (к) — функции, имеющие максимум при к = 0 и стремящиеся к нулю при к ^ ». При ^12 << 1 объектную волну можно представить в виде суммы идеальной волны, амплитуда которой прямо пропорциональна комплексносопряженной амплитуде сигнальной волны, и волн, несущих частично искаженную информацию, с амплитудами -fT (к) и -fc (к). Характер зависимости ширины полосы пространственных частот объектной волны с амплитудой -fT (к) от параметров нелинейной среды качественно совпадает с аналогичной зависимостью для объектной волны с амплитудой A4т 1 [6].

Заключение

• 1.    Для вырожденного четырехволнового преобразователя излучения с учетом термодиффузионной и электрострикционной нелинейностей получено аналитическое выражение, связывающее пространственные спектры объектной и сигнальной волн.

• 2.    Показано, что учет электрострикционной нелинейности приводит к возникновению двух дополнительных динамических решеток и, как следствие, двух дополнительных составляющих объектной волны. Модули пространственных спектров этих волн с увеличением пространственной частоты выходят на постоянное значение, определяемое коэффициентом поглощения и толщиной среды. Существует пространственная частота к ® 2а, при которой коэффициент отражения объектных волн, связанных с наличием электрострикционной нелинейности, равен нулю.