Пространственная селективность четырехволнового преобразователя излучения в поглощающей двухкомпонентной среде при больших коэффициентах отражения

Одним из важных элементов, используемых в системах нелинейной адаптивной оптики, является многоволновой, в частности, четырехволновой преобразователь излучения, который осуществляет обращение волнового фронта падающей (сигнальной) волны и может быть реализован с использованием сред с различными механизмами нелинейности, ответственными за изменение в среде под действием излучения комплексной диэлектрической проницаемости [1–2].

Как правило, в средах одновременно реализуются два и более механизмов нелинейности. Так, в средах с резонансной нелинейностью на параметры четырехволнового преобразователя излучения может существенно влиять тепловой нагрев среды в результате поглощения лазерного излучения [3–7], в обратимой фотохромной среде на параметры четырехволнового преобразователя излучения влияет диффузия фотохромных частиц [8–9] и т. д. Учет нескольких механизмов нелинейности даже при малом коэффициенте отражения часто не приводит к аддитивному сложению амплитуд объектных волн, возникающих при четырехволновом взаимодействии на отдельных механизмах нелинейности [10]. Задача определения пространственных характеристик четырехволнового преобразователя излучения при наличии нескольких механизмов нелинейности существенно усложняется при больших коэффициентах отражения, когда амплитуда объектной волны сравнима или превышает амплитуду сигнальной волны [11–13].

В работах [14–16] в приближениях как малых, так и больших коэффициентов отражения (преобразования) рассмотрены пространственные характеристики четырехволнового преобразователя излучения в прозрачных двухкомпонентных средах с учетом направлений распространения, расходимости волн накачки. Однако в реальных многокомпонентных средах всегда присутствует поглощение на частотах взаимодействующих волн. В поглощающих двухкомпонентных средах, наряду с электрострикционным механизмом нелинейности, эффектами Дюфура, Соре реализуется тепловой механизм нелинейности, увеличивается число динамических решеток, формирующих волну с обращенным волновым фронтом.

Целью настоящей работы является исследование пространственной селективности четырехволнового преобразователя излучения в поглощающей двухкомпонентной среде с учетом больших коэффициентов отражения .

• 1.    Модель четырехволнового взаимодействия

Рассмотрим плоский слой поглощающей двухкомпонентной среды, заключенной между плоскостями z = 0 и z = £ (рис. 1) и состоящей из жидкости и растворенных в ней микро- или наночастиц (суспензии, эмульсии, коллоидные растворы и т. д.). В среде распространяются навстречу друг другу две плоские волны накачки с комплексными амплитудами A 1 - ( r ) = = A V I - ( z ) exp ( — ik 1 - r ) ( / - — волновые вектора волн накачки, r { р ( x , y ) , z } — радиус-вектор) и сигнальная волна с комплексной амплитудой A ₃. Зависимость интенсивности излучения, распространяющегося в среде, от пространственных координат приводит, вследствие явления электрострикции и термодиффузионного эффекта Соре, к пространственному изменению концентрации частиц 5 С , а учет поглощения излучения и эффекта Дюфура – к пространственному изменению температуры среды 5 T . В результате записывается решетка показателя преломления.

Вследствие вырожденного четырехволнового взаимодействия в нелинейной среде генерируется объектная волна с комплексной амплитудой A ₄ , распространяющаяся навстречу сигнальной волне.

Уравнение Гельмгольца, описывающее вырож- денное четырехволновое взаимодействие в глощающей нелинейной среде, имеет вид [2;

по-

V² + k ²

V

Здесь 4

+ — dn 5 T - 2 ik a

n ₀ dT

( A + A *) = 0.

A = ^ A j ; k = to n о c 1 ;

to

–

j = 1

циклическая частота;

n ₀ – среднее значе-

ние показателя преломления dn рость света в вакууме;

среды; c

–

ско-

термооптический

–

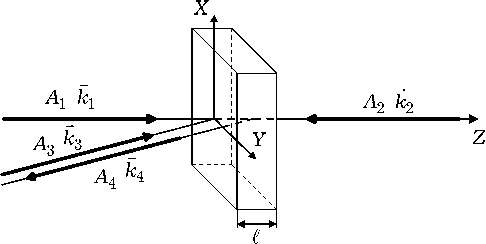
Рис. 1. Схема четырехволнового взаимодействия со встречными волнами накачки

коэффициент; a — амплитудный коэффициент поглощения среды.

Уравнение Гельмгольца записано при условии, что вкладом изменения концентрации частиц в изменение комплексного показателя преломления можно пренебречь. Для типичных двухкомпонентных сред, используемых в работах по исследованию четырехволнового взаимодействия, это условие реализуется при концен- 12     - 3

трациях частиц менее 10 см [17–19].

Дополним уравнение (1) стационарным материальным уравнением, описывающим изменение температуры [20]

• D. v ² 5 T = -2a I + ^ D ¹² V² 1 .                    (2)

• ¹                 D 22

• 2.    Четырехволновое взаимодействие с учетом температурной решетки, возникающей при интерференции первой волны накачки и сигнальной волны

  в

  
  

Здесь D 1 = D_n - D 12 D 21 D —¹ ; D_n и D— — коэффициенты теплопроводности и диффузии; D ₁₂, D ₂₁ и у — коэффициенты, характеризующие эффекты Дюфура, Соре и явление электрострикции соответственно; I = AA * — интенсивность излучения.

Рассмотрим четырехволновое взаимодействие приближении заданного поля по волнам на- качки

(|A12I >> A3 41) и малого коэффициента отражения (|A4 << A31). Тогда выражение для интенсивности излучения, распространяющегося в нелинейной среде, включает в себя сумму интенсивностей волн накачки (I12 = A12 Ay 2) и слагаемые, отвечающие за интерференцию первой волны накачки и сигнальной волны

I = I 1 + 1 2 + A 1 A 3 + A i A 3 . (3)

Представим изменение температуры в виде суммы быстро ( 5 T 31 ( р, z ) ) и медленно ( ⁵ T 0 ( z ) ) меняющихся в зависимости от поперечных координат составляющих. Сигнальную и объектную волны разложим по плоским волнам, быстро меняющуюся составляющую температуры – по гармоническим решеткам.

В приближении медленно меняющихся амплитуд при квазиколлинеарной геометрии взаимодействия волн с учетом граничного условия A4 (р, z = £) = 0 пространственный спектр объектной волны AA4 (к4, z) на передней грани нелинейного слоя связан с пространственным спек- тром температурной решетки 5T31 (кт1, z) следующим образом [16]

• -             — dn -

• A4 (к4, z - 0) - -i   — A20 х

n0 dT г                                                           (4)

х 1 5 T 31 ( к T 1 , z ) exp [- i ( — 2z - — 4 z ) z ] dz .

Здесь

A 4 ( к₄, z ) - A ₄ ( к₄, z ) exp [ P ( г ) - P ( z ) ];

P ( z ) ^- a z + i — dn f⁵ T 0 ( z 1 ) ^dz 1 ;

n ₀ dT ₀

A 20 ^- A 2 ( ^{z - г} ) ^{; к} T 1 ^{- к} 1 ^{- к} 3 ^{; к} 4 ^{- к} T 1 ^{+ к} 2 ^;

кj — поперечная составляющая волнового вектора kj; кт 1 — волновой вектор температурной решетки; k2z и k4z – продольные составляющие волновых векторов второй волны накачки и объ- ектной волны; j - 1 ^ 4.

Для нахождения пространственного спектра температурной решетки воспользуемся вытекающим из (2) уравнением, связывающим 5 T 31 ( к т 1 , z ) и пространственный спектр сигнальной волны на передней грани нелинейного слоя A з ( к з , z - 0 ) , вида [20]

f d. I dz²

-

)

^к T 1 ⁵ T 31 ^(к T 1 , ^{z ) +}

+ 71 A 10 A 30 ( ^к 3 ) ^ex P ( ^- V 1 ^z ) ^- 0,

D ₁

где кT1 - |кT1 ; A10 - A1 (z - 0) ;

A 30 ^(к 3 ) ^- A 3 ^(к 3 , ^{z - 0 ) ;}

P 1 ^{- 2 a-}Y- 12. 0 ^-к T 1 );

D ₂₂

V 1 ^{- 2 a} + i ( ^k 1 z ^{- —} 3 z ) ^;

k1z и k3z – продольные составляющие волновых векторов первой волны накачки и сигнальной волны.

Решение уравнения (5) с учетом неизменности температуры на гранях нелинейного слоя ( 5 T 31 ( к t 1 , z - 0 ) - 5 T 31 ( к t 1 , z - г ) ) имеет вид

5 T 31 ( к т 1 , z ) -

-    / ^ ₂ x A 10 A 3 0 ( ^к 3 ) vAz х

D 1 ( v 2 -к Т 1 )              [ sh ( ^к T 1 ^г )

х { exp ( -у₄ г ) sh ( к т 1 z ) - sh [к т 1 ( z - г ) ] } - ^- exp ( ^- V 1 ^z ) ].

Подставив выражение для пространственного спектра температурной решетки (6) в (4) и проинтегрировав по координате z, получим пространственный спектр объектной волны на передней грани нелинейного слоя

A 4 ( к 4 , z - 0 ) -

• .        к В 1          dn           3 / — х

• ^- - i      / 2 2Ч     A 10 A 20 A 30 ^(к 3 ) ^х

• П 0 D 1 ( v i - к² т 1 ) ^dT

^х I 9 eh Г¹ А { ^[ exp ^(- ^ 1 ^г ) ^- exp ^(-к Т 1 ^{г )} ] ^х

• 2 Sh I к Т 1 г I

exp { [к т 1 - i ( — 2 z - — 4 z ) ] г } - 1

• ^к T 1 ^- i ⁽ k 2 z ^{- к} 4 z )

+ [exp (-у4г) - exp (ктр^)] х х exp {-[кт 1 + i (—2z - k4z )] г}- 1 +

• ^к T 1 ⁺ i ^{( k} 2 z ^{- к} 4 z )

  
  

exp ^[-(a + i А ) ^г ] ^{- 1}'

+------------7-------- .

• a + i А        J

Здесь А - —1 z + —2z - —3z - —4z — проекция волно- вой расстройки на ось Z.

Введем коэффициенты отражения на высоких ( R 1 ) и низких ( R 2 ) пространственных частотах

^A 4 (|к₄| ^ 0.1 — , z - 0 )

R 1 -

^*

.A

R 2 -

x A 4 (|к4| ^ 0, z - 0 )

А * A 30

Из (7) следует, что

R 1 -

R 2 -

G Y D 12 exp ( ^{- 2 а г} ) ^{- 1}

D 22      2а г

G I D 12.1 D 22-- 1 |х

D22 V 2аУD12   J х/1 [1 + exp (-2«г)1+ exp 2"" 1)

[ 2^{[         v      7]}         2а г

Здесь G ²

^- G 1 G 2 , G 1,2 ^-

—г dn n0D1 dT

I 1,2 .

При а ^ 0 коэффициент отражения R1 полностью определяет эффективность четырехволнового преобразователя излучения в прозрачной двухкомпонентной среде [15]. Коэффициент отражения R2 при у ^ 0 определяет эффективность четырехволнового преобразователя на те- пловой нелинейности [11].

Из выражения (10) следует, что коэффициент отражения на низких пространственных частотах R2 равен нулю: 1) для прозрачной нелинейной среды; 2) для поглощающей среды при выполнении условия у - D22/(2aD12).

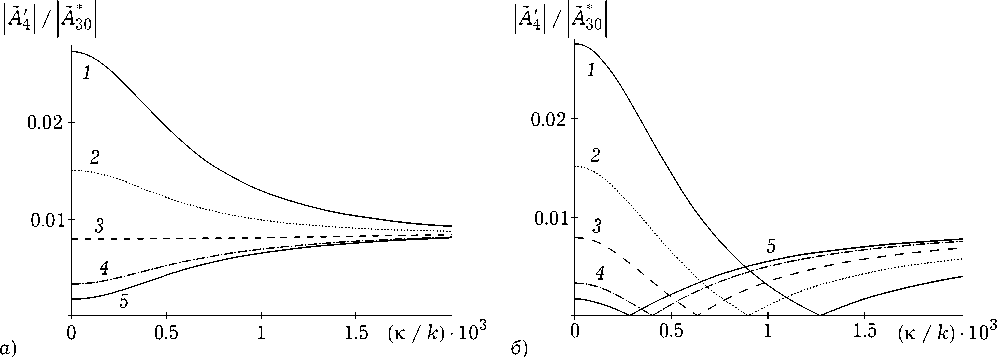
Рис. 2. Пространственные спектры объектной волны при k t = 5 ■ 10 3 , G = 1, у D ^/( D 22 I ) = 10 2 ( а ), - 10 ² ( б ), a t = 2 ■ 10 ¹ ( 1 ), 10 ^{- 1} ( 2 ), 5 ■ 10 ^{- 2} ( 3 ), 2 ■ 10 ^{- 2} ( 4 ), 10 ^{- 2} ( 5 )

В случае слабопоглощающей среды ( a t << 1 ) отношение коэффициентов отражения на низких и высоких пространственных частотах прямо пропорционально отношению коэффициентов поглощения и электрострикции

R 2 = D 22 t ²a

R 1     6 D 12 I y|

Выражение (11) позволяет оценить, при каких толщинах нелинейного слоя, параметрах нелинейной среды пространственный спектр объектной волны обусловлен как тепловой нелинейностью, так и электрострикцией, эффектами Дюфура и Соре

ственном спектре объектной волны наблюдается «провал» на пространственной частоте К 0 , значение которой меняется пропорционально

² D 22 ^aKD 12 ^{k 2} l^Yl).

Для характеристики пространственной селективности четырехволнового преобразователя излучения в поглощающей двухкомпонентной среде с отрицательным коэффициентом электрострикции введем три параметра: полуширину

0.2 <

D ^A <  5 6 D 12 |y      .

На рис. 2 для волн накачки, распространяющихся строго вдоль оси Z ( k 1 _z = - k 2_z = k ) , для сигнальной волны от точечного источника ( AV 30 ( к з ) = 1 ) представлены характерные графики амплитуд пространственных спектров объектной волны при различных значениях коэффициента поглощения. Как при положительных (рис. 2, а ), так и при отрицательных значениях коэффициента электрострикции (рис. 2, б ) амплитуды пространственных спектров с ростом пространственной частоты ( к = |к 4 |) выходят на постоянное значение, определяемое выражением (9).

При положительном значении коэффициента электрострикции выход на постоянное значение амплитуды пространственного спектра объектной волны происходит либо при ее монотонном убывании с отклонением не более 5%, либо при ее монотонном возрастании (рис. 2, а ).

При отрицательном значении коэффициента электрострикции (рис. 2, б ) в простран-

полосы пространственных частот, вырезаемых четырехволновым преобразователем излучения ( Ак = К 1 ) ; полуширину полосы пространственных частот, эффективно преобразуемых в области низких пространственных частот ( Ак ) ; ширину «провала» ( АК 2 = к - К 2 ) , определяемые из уравнений

I A 4 ( К 1,2 , z = 0 )| = 1 A 4 ( к ^ 0.1 k , z = 0)|,       (12)

|A 4 ( Ак 1 , z = 0)| = 1 A 4 ( к ^ 0, z = 0)|.          (13)

Здесь к 1 > К .

При условии R 1 / R 2 > 1 пространственная селективность четырехволнового преобразователя

излучения характеризуется параметром Ак, а при условии R 1 / R < 1 — параметрами Ак и Ак 2 .

На рис. 3 приведены характерные графики зависимости Ак, Ак и Ак 2 от коэффициента поглощения при фиксированном значении

у. Указанные зависимости приведены для Ак в

диапазоне a <6 D 12

a> 6 D 12 |у|/ ( D 22t² ) .

I Y^ ( D 22 ^{t 2} )

, для Ак и Ак 2 —

Значение a =

6 D 12 |y|/( D 22 t ² )

соответствует равенству коэффициентов отра-

жения на высоких и низких пространственных

частотах.

С ростом a наблюдается монотонное увеличение всех трех величин. Характер указанных

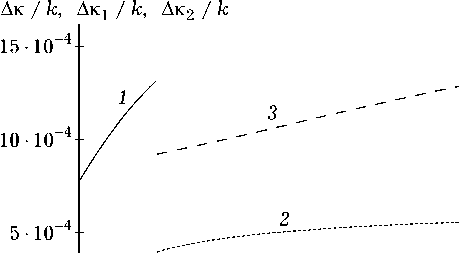
В выражение для интенсивности распространяющегося в нелинейной среде излучения (6) добавляются слагаемые A2A4 + A244, а в изменение температуры – еще одна быстро меняющаяся от поперечных координат составляющая 5T42 (р, z) , которая так же раскладывается по гармониче- ским решеткам.

При квазиколлинерном распространении взаимодействующих волн уравнения, описывающие

-I--------------------------------------------------1--------------------------------------------------1--------------------------------------------------H

0              0.1             0.2              0.3

Рис. 3. Зависимости полуширин полос вырезанных ( 1 ), эффективно преобразуемых пространственных частот ( 2 ), ширины «провала» ( 3 ) от коэффициента поглощения при k / = 5 ■ 10 3 , у D ₁₂/ ( D ₂₂^ ) = - 10-²

зависимостей в области значений а/ < 3 ■ 10 1 хо- рошо аппроксимируется следующими выражениями

Ак = B 1 3 D 12 М к N D 22/

+ а / ,

AS k = B 1 ln² ( В ₂а / + 1 ) ,

^Ак 2 = B ₃ + B 4 а/,

k

где B , B ₁, B ₂, B ₃ , B ₄ – константы, равные при к / = 5 ■ 10³, у D 12/( D 22 / ) =-10 ^{- 2} соответственно B * 4.32 ■ 10 ^{- 3}, B 1 * 9 ■ 10 ^{- 6}, B ₂ * 10 4 , B ₃ * 8.2 ■ 10 ^{- 4}, B 4 * 1.55 ■ 10 ^{- 3}.

изменения пространственных спектров сигнальной и объектной волн, имеют вид [11]

dA 3 • к dn ( г m*

• —    + i       1 ⁵ T 31 + ⁵ T 42 I A 10 x

dz    n0 dT x exp [-i (k1 z - кзz) z] = 0, dA4 . к dn / ~      ~*

• —--i        I ⁵ 7 31 + ⁵ T 42 ) 2A 20 ^x

3. Четырехволновое взаимодействие с учетом температурных решеток, возникающих при интерференции волн накачки с сигнальной и объектной волнами, самодифракции волн накачки

dz    n0 dT x exp [-i (кz - к4z) z J = 0.

Здесь A 3 ( к з , z ) = A 3 ( к з , z ) exp [ P ( z ) ], ⁵ T 42 ( k t 2 , z ) и к t 2 — пространственный спектр и волновой вектор решетки, возникающей при интерференции второй волны накачки и объектной волны.

Учет самодифракции волн накачки приводит к появлению в системе уравнений (15) слагаемых, **

прямо пропорциональных 5 T 31 A 1 и 5 T 42 A 2 . Сла-га-емые, пропорциональные 5 T 42. 4 1 и 5 T 31 AA 2 учитывают перекачку энергии из сигнальной волны в объектную, и наоборот.

Используя материальное уравнение (2), получим систему уравнений для пространственных

Рассмотрим четырехволновое взаимодействие при интенсивностях объектной волны сравнимых или даже превышающих интенсивность сигнальной волны (реализуется случай больших коэффициентов отражения). Тогда, наряду с температурной решеткой, возникающей при интерференции первой волны накачки и сигнальной волны, необходимо учитывать температурную решетку, возникающую при интерференции второй волны накачки и объектной волны. Существенное влияние на четырехволновое взаимодействие начинает оказывать самодифрак-ция волн накачки.

спектров температурных решеток

(dL dz1

-

^x I 2V 1

(dl dz 2

)

^к T 1 ⁵ ^ T 31 ^(к T 1 , ^z ) =

A

- yexP (-V1z) x

Y D 12 d

D ₂₂ dz

-

+ в 1 I A 3 * ( к з , z ) ,

2 о     i —      X кT2 5T42 (кT2, z) =

(16) ^A

^- D -exp (-V 2 z ) ^x

x 12^2 ^ D ¹²- d + ₽ 2 1 4A 4 * ( k 4 , z ) .

(     D 22 dz J

Здесь

₽ 2 = ^--уА² ( v i ^-k T 2 ) , D 22

^v 2 = ^{2 a +} i ( ^к2z ^{- к} 4 z ) , ^k T 2 = |^k T 21 = ^k T 1 .

Продифференцировав систему уравнений (15) дважды по координате z и учитывая (16), получим систему дифференциальных уравнений третьего порядка, связывающую пространственные спектры сигнальной и объектной волн

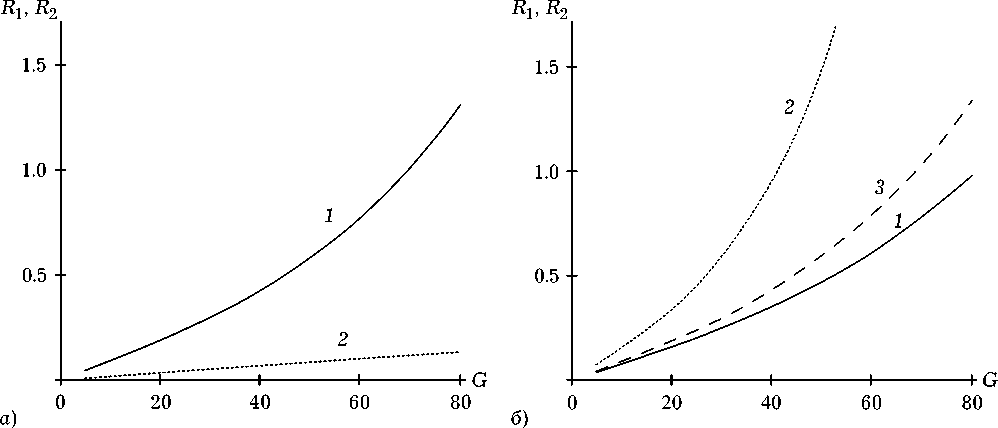
Рис. 4. Зависимости коэффициентов отражения на высоких ( 1 ), ( 3 ) и низких ( 2 ) пространственных частотах от интенсивности волн накачки при k £ = 5 ■ 10 3 , у D 12/ ( D 22 £ ) = - 10 ^{- 2}: а ) а £ = 10 2 ; б ) а £ = 10 ^{— 1} ( 1 , 2 ), 0 ( 3 )

d 3 A 3                d 2 A 3         Y D ₁₂ *

--- —+ 2 i ( к — ko_z ) 5— 2 iG     v x dz ³       ( ¹ z    ³ z ) dz ²    I ¹ D 22 ^

X exp ( —2а z ) + ^[ k T 1 + ( k z — к з z ) ² 4 d 3 —

• —    iGy — exp (—2аz) Av‘ = 2iG Y^12 v2 x £

dA’ x exp [2а (z — £) — iAz]

+ iG в2 exp [2а (z — £) — iAz] A4*, d3 A4            , .d2A4         YD12 *

— + 2 i ( k2 z — k 4 z )   2- + <2 iG 2

dz                  dz I

*w

^X exp [ ^{2 а} ( z ^{— £} ) ] ^— I ^k T 2 + ( k 2 z

+ iG 2 в 2- exp [2а ( z — £ ) ] . 4 4 =

= —2iG Y^12 V1 exp [— (2а + iA) z] -^3— D22£

• —    iG e ^ exp [— ( 2а + i A ) z ] A A 3* .

В предельных случаях при а ^ 0 и Y ^ 0 система уравнений (17) совпадает с аналогичными системами уравнений, связывающими пространственные спектры сигнальной и объектной волн при вырожденном четырехволновом взаимодействии в прозрачной двухкомпонентной среде [15] и в среде с тепловой нелинейностью [11] соответственно.

Численное решение системы уравнений (17) с учетом граничных условий на амплитуды пространственных спектров сигнальной и объектной волн и их производные на гранях нелинейного слоя

dA 3,4	dA 3,4	z = £
dz	dz z = 0

= 0,

вытекающие из неизменности температуры на гранях, позволяет проанализировать пространственную селективность вырожденного четырехволнового преобразователя излучения в поглощающей двухкомпонентной среде с учетом самодифракции волн накачки, перекачки энергии из сигнальной волны в объектную, и наоборот.

С ростом интенсивности волн накачки ( 1 1 = I 2 ) наблюдается монотонное увеличение коэффициентов отражения на высоких и низких пространственных частотах объектной волны (рис. 4). При условии D 22 £ ²аД6 D 12 |y|) < 1 скорость изменения коэффициента отражения на высоких простран

Г dR^)

ственных частотах меньше скорости из-[ dI J менения коэффициента отражения на высоких Г dRi)

пространственных частотах II (рис. 4, а), в ( dI J то время как при D22£2aД6D12 |y|) > 1 наблюдается обратная ситуация (рис. 4, б). Таким образом, с ростом интенсивности волн накачки разность коэффициентов отражения R1 и R2 увеличивается.

Учет поглощения излучения двухкомпонентной средой приводит к уменьшению скорости роста коэффициента отражения на высоких пространственных частотах (рис. 4, б , кривые 1 и 3), при этом скорость роста коэффициента отражения на низких пространственных частотах меняется незначительно (рис. 4, б , кривая 2).

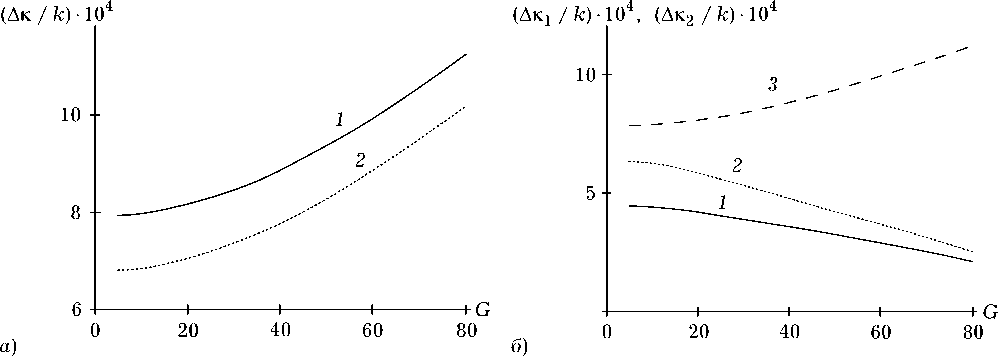
Рис. 5. Зависимости полуширин полос вырезанных ( а ), эффективно преобразуемых пространственных частот ( б , кривые 1 , 2 ), ширины «провала»» ( б , кривая 3 ) от интенсивности волн накачки при k t = 5 ■ 10 3 : а ) a t = 10 - ( 1 ), 0 ( 2 ), у D 12/( D 22 t ) = - 10 - 2 ; б ) a t = 10 ^{- 1}, y D ^/( D a t ) = - 10 ^{- 2} ( 1 , 3 ), 0 ( 2 )

При at = 10 1 относительная разность скоростей dR роста для четырехволновых преобразователей излучения в поглощающей двухкомпонентной среде и в среде с тепловой нелинейностью в диапазоне нормированных интенсивностей волн накачки G от 5 до 80 не превышает 10 %.

При отрицательных значениях коэффициента электрострикции увеличение интенсивности волн накачки не приводит к смещению положения «провала» κ0 в пространственном спектре объектной волны.

На рис. 5 приведены характерные зависимости полуширин полос пространственных частот, вырезанных четырехволновым преобразователем излучения, эффективно преобразуемых в области низких пространственных частот, ширины «провала» от интенсивности волн накачки.

Рост интенсивности волн накачки приводит к монотонному увеличению полуширины полосы вырезанных частот ∆κ (рис. 5, а ) и ширины «провала» ∆κ₂ (рис. 5, б , кривая 3) и уменьшению полуширины полосы наиболее эффективно преобразуемых частот ∆κ₁ (рис. 5, б , кривые 1 и 2). Для случая четырехволнового преобразователя излучения в прозрачной двухкомпонентной среде (α→0) зависимость полуширины полосы ∆κ от интенсивности волн накачки лежит ниже соответствующей зависимости для случая четырехволнового преобразователя в поглощающей двухкомпонентной среде.

По сравнению с четырехволновым преобразователем излучения в среде с тепловой нелинейностью (γ=0) у четырехволнового преобразователя в поглощающей двухкомпонентной среде скорость убывания полуширины полосы эффек- тивно преобразуемых пространственных частот ∆κ1 с увеличением интенсивности волн накачки оказывается меньше.

Приведем некоторые оценки. Для четырехволновых преобразователей излучения в поглощающей двухкомпонентной среде (у D 12 Д D 22 ® ) = = -10 ^{- 2}) и в среде с тепловой нелинейностью при k t = 5 ■ 10³, a t = 10 ^{- 1} изменение на порядок интенсивности волн накачки (от G = 8 до G = 80) увеличивает коэффициент отражения на низких пространственных частотах в 68.2 и 61 раз соответственно. При этом полуширина полосы эффективно преобразуемых пространственных частот уменьшается соответственно в 2.1 (от ∆κ₁ ≈ 4.4 ⋅ 10 ^{- 4} k до ∆κ₁ ≈ 2.1 ⋅ 10 ^{- 4} k ) и 2.5 раза (от ∆κ₁ ≈ 6.3⋅10 ^{- 4} k до ∆κ₁ ≈2.5 ⋅10 ^{- 4} k ).

Для четырехволновых преобразователей излучения в поглощающей (a t = 10 - ²) и прозрачной двухкомпонентных средах при k t = 5 ■ 10³, у D 12 /( В 22 £ ) = -10 ^{- 2} изменение интенсивности волн накачки в тех же пределах увеличивает коэффициент отражения на высоких пространственных частотах в 18.2 и 18.6 раз соответственно. При этом полуширина полосы вырезанных пространственных частот увеличивается соответственно в 1.4 (от ∆κ ≈ 8 ⋅ 10 ^{- 4} k до ∆κ ≈ 1.1 ⋅ 10 ^{- 3} k ) и 1.5 раза (от ∆κ ≈ 6.8 ⋅ 10 ^{- 4} k до ∆κ ≈ 10 ^{- 3} k ).

Заключение

Для вырожденного четырехволнового преобразователя излучения в поглощающей двухкомпонентной среде в приближении малых коэффициентов отражения получено аналитическое выражение, устанавливающее связь между про- странственными спектрами сигнальной и объектной волн. Показано, что знак коэффициента электрострикции определяет общий вид пространственного спектра объектной волны.

В случае отрицательного значения коэффициента электрострикции существует пространственная частота, на которой амплитуда пространственного спектра объектной волны равна нулю. Увеличение коэффициента поглощения приводит к росту полуширин полос вырезанных, эффективно преобразуемых пространственных частот, ширины «провала».

Соотношение между скоростями изменения коэффициентов отражения на высоких и низких пространственных частотах определяется величиной параметра D 22^2a/ ( 6 D 12 |у| ) . С ростом интенсивности волн накачки увеличиваются не только коэффициенты отражения R ₁ и R ₂, но и их разность.

Полуширина полосы вырезанных пространственных частот и ширина «провала» с увеличением интенсивности волн накачки возрастают, а полуширина полосы эффективно преобразуемых пространственных частот уменьшается.