Пространственная задача Римана для двоякокруговых областей

1. Введение. Интеграл типа Темлякова и некоторые его свойства

Определение 1 (см. [26, с. 349]). Областью D класса (Г) называется полная, ограниченная, выпуклая двоякокруговая область с центром в точке (0, 0) Е D, граница которой дважды непрерывно дифференцируема и аналитически выпукла извне.

Область D класса (Г) (D Е (Г)) допускает следующее параметрическое задание:

В = |J {(w,z) Е С² : |w| < п(т), |z| < г₂(т)} 0^т^1

= inter. P| {(w,г) E С² : с(т)\ w + с?(т)|г < 1}, 0^т^1

где с(т) = тгх 1(т), с/(т) = (1 — т)г2 ^т), Г1(т) и г2(т) — действительные, непрерывно дифференцируемые функции в интервале (0,1), удовлетворяющие условиям

п(0) = 0, 0 < г'^т) ^ п(т)т \                       (2)

т г2(т) = R2 exp

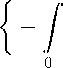
Т

1 — т

сНпг1

и}.

R₂ > 0 (_R₂ = const).

Граница области В Е (Т) имеет вид

ЭВ = {(w,z) Е С² : w < щ (т), z| < г₂(т), т Е [0,1] }

= | (w, г) Е С2 : w| = Г1(т)щ г = г2(т)г/е 'Г 0 < т < 1, 0 < t < 2тг, г/ = l|.

Рассмотрим функцию Ф(т, t, A, /z) (т и t — действительные переменные, А и /z — комплексные), которая суммируема в прямоугольнике R = {(т, t) Е JR² : 0 ^ т ^ 1, 0 ^ t < 2%} при любых А и (.I (|А < +оо, /z < +оо).

Определение 2. Интегралом типа Темлякова I рода будем называть интеграл вида

1 2тг

KW1 Z' = 4Aj

0       0     |^| = 1

где (w, г) E C² , u = c(t)w + d^ze^.

Функции Гх(т) и г2(т) определяются условиями (2) и (3), поэтому можно рассмотреть неаналитическую гиперповерхность

|w|=ti(t),   г|=г₂(т)  (0 <  т < 1),

являющуюся огибающей семейства гиперповерхностей

c(t)|w + с/(т)|г| = 1 (0 <  т < 1)

и расположенную под огибаемой в каждой точке. Из соотношения (1) видно, что областью, границей ЭВ которой является гиперповерхность (5), будет область В Е (Т). Поэтому интеграл (4) получил название интеграла типа Темлякова I рода с определяющей ограниченной областью В.

Известно (см., например, [20, с. 33]), что для функций представимых интегралом типа Темлякова I рода (4), в точках (w,^) Е С2 имеет место формула

( 2тг-у+1/,

J Ат I Ф⁺ (T,t,u,ue~^u) At

TiUT3 ^+v

Ф+ф\

P J Ат J Ф” (t, t, u, ue~^u) At j ,

T2UT3 ф-Т'

где

Ф(тП + 2тг,ц,це”г1) = Ф(т,1,г/,г/е"1*),

Ф+(т,1,и,ие-1*) = — v /L

Z1VL J        7] — u

Ы=1

для u < 1, а функция Ф” (т, t, u, ue~^lt) определяется по той же формуле, но для Ы > 1,

'ффо, г) = arg w — arg z,

{arccosafr, w|, z|),    а(т, w|, z|)< 1, о,               Hl HL H)> i,

7Г,                         a(T, |w|, 2:|)< -1,

«(т, H, И) = (i - c²(t)|w|² - d² (t^z^HMt^MWzW¹ ■

В = {т : c(t)|w + б?(т)И| < 1}, T₂ = {т : c(t)|w - с?(т)|г| > 1},

T₃ = {т : c(t)|w + Н^Т)И > !> Н^Т)Ы ” Н^Т)И ^ O-

Пусть образ границы ЭВ области В в абсолютной четверть-плоскости задается уравнением г = A"(|w|) (или г₂(т) = КфдффУ)- Обозначим через [адД] ф = 1,2,...,п) интервалы изменения параметра т такие, что функция г₂(т) = Кфдфтф линейна на отрезке [ri (аД гх(Д)] ф = 1, 2,... , п), где п(т) = тс”¹ (ц > 0), т Е [ад Д] ф = 1, 2,... , пф

Определение 3. Порядком границы w = ^(|г|) (т₂(т) = K^ti^t^ области В называется число интервалов линейности [т1(а^),Г1(Д)] функции г₂(т) = J^(ti(t)), принадлежащих отрезку [0, ri (1)].

Определение 4. Мы скажем, что функция Ф(т, t, г/, r/e”^lt) принадлежит классу а (Ф Е а), если Ф по г/ удовлетворяет условию Lipa (0 < а ^ 1), независимому от т и t, и ограничена по модулю для (т, t,i^ Е М = {(т, 1дф : (т, t) Е R, г/ = 1}.

Рассмотрим следующие функции:

/1(т, |wL kl) = И - W(t)|w + 7V(t)ti(t) - г₂(т),

№, |w|, |г|) = 2|z| - /i(t, |w|, |z|),

/з(т, |w|, к!) = 2И + ^(т)Г1(т) - Г2(т) - /1(т, |wLkl):

где N^t) = ^(т^г'^т))^-1, 0 < т < 1, причем a = lim N^t), b = lim МфУ t— >-0               t — >1

Используя заданные функции, рассмотрим в пространстве С2 области:

D^ = D= Q {(w^) G С² : ШИН <0},

0^т^1

£)+- = {(w,z) G С2 : /2(т, |wL к!) < °}:

D"⁺ = {(w,z) G С² : /₃(т, |wL kl) < °}:

D~~ = C2\D++ U D+- U D- + , множества

Bs,i = {(w,z) G C2 : w = (1 + s)(2ci) ^ z = (1 - з)(2ф) хщ r/ = 1, с^ > 0, ф > 0 s = ±1, i = 1,2,... , n}, а также следующие области:

• 1)    если cti ф 0, Зп ф 1 (1 <  п < +оо), то

9^{(w,z) G С2 :/1(ай |w|, z|) < 0, /2(1, |w|, z|) < 0, s = +1 или

/1 (А, И И) < °, /з(0, |w|, \ф) > 0, s = -1, г = 1,2,... ,п},

9/i{(w,z) G С² : /1(0, |w|,|z|) < °, ЫЗг, И И) < 0, s = +1 или

/1(1, Н, И) < 0, /₃(а^, |w|, |z|) > 0, s = -1, г = 1,2,... ,п}:

• 2)    если «1 = 0, pi = 1, то

9i+i = 9ti,i = D⁺⁺, qyi = D⁺", qZ_1;1 = D" ⁺ .

Семейство двумерных поверхностей, проходящих через точки окружностей BSii (s = ±1, г — фиксировано), обозначим через стзк^ = {(w’2) е ^2 : И = к^Ц - с^ т), argw - arg г = I

(argO = argwq — I, (wq,0) G В+1ф, s = 1 или г = fc|w + d”1, argw — arg г = I

(argO = argz₀ + 3 (О,г_о) G В_1ф, s = -1,

\k\ < +oc, Z <2%, Z = l,2,...,n|.

Л. А. Айзенберг установил (см., например, [26, с. 352]), что интеграл (4) является функцией голоморфной в областях D⁺⁺, D~⁺ и D^+-, а если Ф G а, то непрерывен во всем пространстве С², за исключением множеств B_Sii (s = ±1, г = 1,2,... ,п).

Определение 5. Множества B_s^ назовем окружностями особенностей интеграла типа Темлякова I рода.

Для интеграла типа Темлякова имеют место следующие утверждения:

Предложение 1 (см. [3]). Интеграл (4) на двумерном многообразии бесконечно удаленных точек С² обращается в нуль, причем, если точка (w,z) стремится к бесконечно удаленной точке вида (тоо,оо( (или (oo,Zq) ), то это стремление происходит произвольным способом; если же точка (w,z( стремится к точке вида (оо,оо), то это стремление должно происходить по пути, расположенному на гиперповерхности г = c^cZ™¹1 w| + b (Ь — произвольное вещественное число).

Предложение 2 (см. [21, с. 12-13]). Пусть граница области D Е (Т) имеет конечный порядок n (1 ^ п < оо), а плотность интеграла (4) функция Ф Е а. Тогда предельные значения интеграла типа Темлякова I рода (4) в точках окружностей особенностей В₈^ определяются по формуле:

1 2тг

f(w₀,z₀) = hm f(w,z)=T—^ dr dt -----------di]

(w,z)->(w_o,zo)e5_S]i               4л²г J J J i] — uq

О о

0г 2?Г

+ ± d1Ф(т,.,„„„„

—

^dt

^^^^^^^™

о

3,

Н = 1

H-VoW

Т U ^.t,W

«i     I — _Vo(k)

—

^dt,

где Ho = c(t)w₀ + d(r(z_oe ^lt, для т E [0,аД U (Д, 1],

г мо = exp -

(1 + s) argw0 + (1 + s)(arg20 + 1) , для т E [а^Д], (wq,Zo) G Bsy s = ±1; особый интеграл в формуле (7) понимается в смысле главного значения по Коши;

ToW = , , 1™ Т^т, |w|, |^|) Vu),z)^Vwo,zo)EB_S)i

' 0,                       (iu,z(

TV,                   (w,z)

arccos(-^)’

-----> (1U_O,Z_O( E B_8>il D++

----------> (1U_O,Z_O( E B_8>il

D+-,D-+

----> (w₀,z₀) G B_sv

D-

Определение 6. Функцию f(w,z( назовем функцией класса (Т) (/ Е (Т)), если она задана в пространстве С², кроме точек окружностей B₈^ (s = ±1, г = 1,2,... ,n\ и удовлетворяет следующим условиям:

• 1)    функция f(w,z( — непрерывна в <С?\В₈у, голоморфна в областях D^^, D D*^-, и обобщенно-аналитична в D ;

• 2)    функция f(w,z( имеет конечные пределы в точках B_s^ (s = ±1, i = 1,2,... , n) при стремлении точки (w, z) из областей D⁺⁺, (или D^{- +}, или D^+-\, имеет предельные значения в точках B_s^ (s = ±1, г = 1, 2,... , п) по путям, расположенным на двумерных поверхностях сГд^’^ (s = ±1, г = 1,2,...,п), если стремление точки (ги,г^ происходит из области D~~.

• 2.    Постановка и решение неоднородной краевой задачи линейного сопряжения функций из класса (Т) (задача Римана)

Из свойств интеграла типа Темлякова I рода с ограниченной определяющей об ластью D Е (Т) вытекает справедливость следующего утверждения

Утверждение 3 (см. [21, с. 13]). Всякая функция, представимая интегралом типа Темлякова I рода (4) с плотноствю из Ф класса а, принадлежит классу (Т).

Пусть в пространстве С² задана область D Е (Т), граница которой имеет конечный порядок п (1 ^ п < ос). Требуется найти функцию f(ji),z^ класса (Т), обращающуюся в нуль на двумерном многообразии бесконечно удаленных точек, удовлетворяющую в точках заданной окружности особенностей

B_Sii = {(w, г) : го = т^с”¹, z = О, r/o = 1, г = 1,2,... , п} (г — фиксировано)

краевому условию

Лф (г/офЛо) = G^o)f - (r/QC^^O) +g(r/o).                   (8)

Функции G(r/o) и g(r/o) заданы на окружности особенностей Byi (г — фиксировано) и удовлетворяют условию Гёльдера, причем G(r/o) ф 0 на окружности Вцп

Решение поставленной краевой задачи будем искать в виде интеграла типа Темлякова I рода с определяющей областью В. По условию В — область класса (Т), граница которой имеет конечный порядок п. Для фиксированного г рассмотрим интервал линейности [гДаДгДД)]. Тогда граница ЭВ области В Е (Т) имеет для этого отрезка вид Ci w + Д|г| = 1, т. е. п(т) = тс^¹, т₂(т) = Д-тЦ^-1 для т Е [а», Д], с^ > О, ф > 0. Рассмотрим сначала решение задачи для случая сц ф 0 и Д ф 1. Подставив формулы (7) предельных значений интеграла типа Темлякова в краевое условие (8), получим

2тг /                       0г                                                                                /

• 1    f             Г                ,   1-G(??o) f Д '^ф(^тД,и_о,и_ое ^dr

—   < (1 + G(i]0^ Ф(тД,ио,иое uJdr^--:--- —!с

4% J         J                  mJ       т] - и₀

0 ^v                  at                                                     7)1 = 1

1-ОЫ Г Г Ф(т,1,ио,иое-^)1

4--dr ------------------di] — 2g(r/₀) > dt = и.

m J J f/ - Mo

To 7)| = 1

где

То = [0, оф U (Д, 1],

[ exp {г arg ^}, ^U0 = < _T . 7)0    '

( 7’1 (t) Cj ’

т Е т Е

К, Д]

То.

Отсюда следует, что

[1 + G(7?O)]F[a.i|g.](f,7)o) + -

-сы Г ivi J 17)1 = 1

d - 1/0

di]

+ I K^^^o^FT^t,^ dT] = 2(дДо) +

0^,

| Г)| = 1

2тг где f y(t,r/o) dt = 0 и ф(1,г/0) — некоторая функция непрерывная по t G [0,2я] и о удовлетворяющая условию Lipa (0 < a ^ 1) независимому от t,

^[a.,/3.]

/3.

(Mo) = I

Ф(тД,и_о,и_ое ^г13<1т,

оц

К^тр^Е^,^ =

i - сы тгг

/

To

ф^лМоич^!!

1 п(т) Cj

At.

Полученное уравнение (9) есть полное особое интегральное уравнение с ядром Коши, общая теория решения которого хорошо разработана (см., например, [7, с. 185-195]).

Для некоторых частных случаев области D G (Т) уравнение (9) сводится к простейшему случаю особого интегрального уравнения — характеристическому уравнению, которое решается в замкнутой форме. Например, пусть а^ = 0 и Д = 1, тогда область D Е (Т) есть область типа А, а уравнение (9) принимает следующий вид:

[1 + G(77o)]K[O,i](t,r?o) = ---^^ [ ^^^-dTi = 2(д(ц0) + ф(Д7,0)), тгг J т] - з/о

Ы=1

т. е. характеристическое уравнение. Этот случай рассматривался нами ранее (см., например, [10, с. 14-15]), получено решение задачи в замкнутой форме.