Пространственное моделирование нестационарной стадии истечения вскипающей жидкости из камер высокого давления

Истечение двухфазных смесей из труб и сопел является элементом многих технологических процессов современной энергетики, нефтегазовой промышленности, ракетной техники и других отраслей [1, 2]. Струи жидкостей, возникающие в результате мгновенной разгерметизации сосудов высокого давления как элементов сложных конструкций и сооружений, приводят к серьезным промышленным авариям. Возрастающие требования к обеспечению безопасности производственных объектов определяют актуальность и необходимость теоретического исследования и пространственного численного моделирования нестационарных процессов взрывного истечения пароводяных смесей из сосудов высокого давления.

Изучению вопросов истечения двухфазных потоков посвящены работы А.И. Ивандаева, А.А. Губайдуллина [3], A.R. Edwards, T.P. O’Brien [4], Р.И. Нигматулина [5], В.Ш. Шагапова [6], G.A. Pinhasi, A. Ullmann, A. Dayan [7], О.Е. Ивашнева [8] и другие. Высокие значения температуры и давления в емкостях с водой при разгерметизации приводят к ее быстрому расширению и вскипанию. Начальная, нестационарная, стадия истечения вскипающей жидкости представляет особый интерес как в теоретическом, так и экспериментальном плане, поскольку характеризуется значительными метастабильными волновыми процессами. Подробно эта проблема на основе экспериментов [4] в одномерной постановке рассматривалась В.Ш. Шагаповым [6], О.Е. Ивашневым [8], Р.Х. Болотновой и другими [9]. В цитируемых работах изучались нестационарные процессы истечения вскипающей воды при разгерметизации трубы высокого давления, сопровождающиеся образованием быстрой волны разрежения и установлением режима истечения, когда длительное время поддерживается постоянное давление, соответствующее перегретому состоянию.

Численное моделирование процесса образования струи вскипающего теплоносителя с учетом неравновесности пароводяной смеси вблизи границы разрыва представлено в [10]. Для решения задачи

авторы прибегают к модели идеальной сжимаемой жидкости в квазистационарном приближении. В [11] анализируются эксперименты по взрывному вскипанию струй воды в результате истечения через тонкое цилиндрическое сопло из сосудов высокого давления. В зависимости от начальных параметров жидкости, близких к термодинамической критической точке, реализуются различные режимы истечения с углом распыла струи, зависящим от начальной температуры: от конической формы до ее полного «развала», когда струя захватывалась внешней поверхностью рабочей камеры и растекалась вдоль ее поверхности.

Целью настоящей работы является численное моделирование и изучение пространственной динамики нестационарной начальной стадии истечения двухфазного потока при внезапной разгерметизации сосудов высокого давления в условиях экспериментов [11] с последующим процессом образования дозвуковых и сверхзвуковых течений вскипающей пароводяной смеси и структуризацией формирующегося потока в зависимости от начальных условий. Использование в работе единого широкодиапазонного уравнения состояния воды и пара, полученного Р.И. Нигматулиным, Р.Х. Болотновой [12] в аналитической форме, описывающего экспериментальные данные на линии насыщения в области однофазных и метастабильных состояний, позволило осуществить исследования динамики истечения вскипающей жидкости в большом диапазоне изменения термодинамических параметров.

1.    Модельные уравнения

Запишем систему дифференциальных уравнений для газожидкостной смеси. Для газожидкостных смесей условия совместного деформирования фаз сводятся к уравнениям, определяющим объемное содержание фаз a i = VjV ( V i , V — удельные объемы фазы и смеси; i = g , l — индексы соответствуют газообразной ( g ) и жидкой ( l ) фазам), и можно предположить, что имеет место равенство как скоростей движения фаз, так и давлений в них [5].

Исходя из уравнений механики двухфазной смеси, в двумерном случае пространственной осевой симметрии (при этом x и y — соответственно осевая и радиальная эйлеровы координаты) система будет включать [13]:

– уравнения неразрывности фаз смеси:

• ^{d p}     Q ^{d a}^      Q

  J g ,

  
  

a, —- + p0 —- + a,p0div v = l dt ldt l l dpgо a ., + P dt

d a

—- + a dt

.g p ⁰ g div v = J g ;

– уравнения движения смеси:

dv_x  d p             dv y д p

p —- + —= 0,     p —- + —= 0, dt   dx              dt   8у где t — время; p0 — текущее значение плотности i-й фазы; p = p0 - a; + pg - ag и p0 — средняя текущая и начальная плотности смеси; p(p0, T) — давление, зависящее от текущего значения плотности p0 и температуры T ; v — вектор скорости движения фаз с проекциями vx, vy на соответствующие оси; Jlg — интенсивность переноса массы в единице объема смеси из фазы l в фазу g .

Используя условие аддитивности внутренней энергии смеси e ( p 0 , T ) по массе, выразим ее через внутренние энергии фаз e i [5]: p e = e l p 0 a _; + e_g p g a _g и представим закон сохранения энергии смеси для двумерного случая в виде:

de        de g

• ^{a 1} p i     ^+a g p g     ⁺ p ^{div v} = J g ⁽ e ' ^- e g ) ,

dt         dt

p ( р 0 , T ) = p ⁽ p Чр 0 ) + p ⁽ T ⁾( р 0 , T ),      e ( р 0 , T ) = e ⁽ p ) ( р 0 ) + e ^{( T )} ( T ) + e ⁽ ch ) .

Здесь e ^(c h ) — величина, необходимая для согласования внутренних энергий паровой и жидкой фаз.

Температура насыщения T_S ( p ), теплота парообразования l_S ( T ) и радиус пузырьков a ( x , y , t ) определяются аналогично работе [9] по следующим формулам:

T_s ( p ) = T

—

T .

In ( p_s^{( T} )/ p . ) ,

l_s ( T ) = h * . ( 1 — TT ) ⁰ ’ ³⁶⁷ ,

^{3 a} g ⁽ x , y , t ) a ( x , y , t ) = ³--------------- ,

\ 4 n n ( x , y , t )

где p , = 20,2 - 10⁹ Па; T , = 4200 K; T„ = 31K; h , = 30,7 - 10⁵ Дж/кг, n — число пузырьков; T_cr , h * — константы, определяющие теплоту парообразования [9].

Интенсивность фазового перехода вода-пар J_lg (кг/(м³с)) зависит от числа ( n ) и радиуса ( a ) пузырьков, температуры насыщения T_S ( p ), теплоты парообразования l_S ( T ) и коэффициента теплопроводности X l (кг м/(с³ K)) [9]:

J_lg ( x , y , t ) = 2 n a ( x , y , t ) n ( x , y , t ) Nu

X i ( T — T ( p ) ) l s ( T )

X l = 56,4 - 10 ^{— 2}.

Здесь Nu — число Нуссельта, для которого используется аппроксимация из [14], полученная на основе решения, взятого в [15]: Nu = ( 12Ja/п ) [ 1 + ( ^2 ) ( n/6Ja ) ^2/3 + n/6Ja ] , где Ja = c_pl р ⁰ ( T — T_S ( p ) )Д l_S(T ) р ^ ) — число Якоба; c, — удельная теплоемкость воды при постоянном давлении.

В настоящей работе предполагается, что фазовый переход в процессе кипения (2) осуществляется в условиях перегретого состояния, когда температура смеси превышает температуру насыщения: T — T_S ( p ) >А T , где A T = 10 K — перегрев жидкости. Долговременное нахождение жидкости в неравновесном перегретом состоянии объясняется капиллярными эффектами на межфазной границе (см. [9]), когда процесс кипения происходит при ограниченном радиусе пузырьков, а увеличение паросодержания связано с образованием новых пузырьков на неоднородных примесных частицах. На завершающей стадии процесс кипения становится равновесным ( A T = 0 K) и при постоянном числе пузырьков поддерживается за счет роста их радиуса [9].

2.    Методика численного решения

При численном решении задачи исследования осесимметричного движения пароводяной среды применялись подвижные (лагранжевы) сетки, а также метод сквозного счета, предложенный М.Л. Уилкинсом для решения задач динамики сплошной среды [16].

Лагранжевы сетки придают методу сквозного счета некоторые преимущества перед другими численными методами при решении задач динамики двухфазной газо- или парожидкостной среды. Используемая естественная аппроксимация производных по пространственной координате [16] позволяет численно решать задачу на деформирующейся во времени лагранжевой сетке. Кроме того, сетка, связанная со средой, дает возможность контролировать массу каждой ячейки двухфазной смеси, и вследствие этого упрощается расчет тепломассообменных процессов при фазовых превращениях.

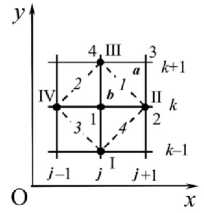
Рис. 1. Схема расчетной сетки

При разбиении расчетной области на элементы с помощью четырехугольной сетки, движущейся вместе со средой (Рис. 1), с узлами сетки 1, 2, 3, 4 соотносились начальные значения скоростей, а с центрами ячеек 1 , 2 , 3 , 4 — начальная плотность, температура, газосодержание. Обозначения j , к определяли местоположение узлов на расчетной сетке в координатной системе O xy : узел I имеет номер ( j , к — 1),

II — ( j + 1, к ), III — ( j , к + 1), IV — ( j — 1, к ).

В начальный момент времени массы фаз и общая масса смеси вычислялись для каждой ячейки в соответствии с [16]. Так, в элементе 1 масса фазы l составляла

Mi = ¹ ^ ° (( У 0 + У з° + У 4' ) A ° + ( У 0 + У г ' + У 4' ) А »’) ; относительный объем в момент времени t , то есть на 3 ^ V ' J               -⁴, a V¹                1„                                                         "

" -м шаге по времени, определялся согласно уравнению сохранения массы:

У = ¹ fl? 1 (( У "  + У "  + У " ) А П + ( у " + У "  + У 4 ⁿ ) A b ), ,                          (3)

3 ^ M J 1¹

где A " , A " — площади треугольников а и b : A " = ( x " ( у ₃ " - у " ) + x ₃ " ( у " - y " ) + x " ( y " - У П ) ) /2, A bi = ( x П ( У 4 - У п ) + x П ( У п - У П ) + х П ( У П - У П ) ) /2- При этом площадь четырехугольного элемента вида 1 в момент времени t_b составляла: A - = A "1 + A_b" , где п — номер шага по времени. Далее, с учетом выражения (3), находилась масса каждой фазы m 1 = р_и a l y - и m_gi = р _gi а _giV .

Уравнения движения (1) использовались для отыскания скоростей узлов расчетной области, которые центрировались в точке j , к и вычислялись, как и в [16], на половинном шаге по времени t " ^{+ V2} = t " + A t /2 :

n

• • и+1/7       • И —1/7       1—AV         И I И       И \       И I И        И \       И / И        Их       И I и       и \

xj , к  = xj , к  ⁺ ^Г " ^- [_ pi ( ^y II - ^y III ) ⁺ p2 ( ^y III - ^y IV ) ⁺ p3 ^{( y} IV - ^y I ) ⁺ p4 ( ^y I - ^y II )_ | ,

^{2 ф} j , к

n

+1/2     "IV At "  v"   v"      "п v" v" r>" v" v" -n" v" v"V\ yj, к     yj, к  + ~ I"  |_ pi ( x II   x III ) + p2 ( x III   x IV ) + p3 ( x IV   xI ) + p4 ( xI   x II )J ,

^{2 ф} j , к

1 4

fft A v

♦ П . к = V S

⁴ i = 1

Затем устанавливались координаты сетки на новом временном шаге: x" ^¹ = x" _fc + x "У2 A t" ^+1/2 , V " ⁺¹ = v " + v " ^+V2A " + ^{+V2 y} j . к    ^y j . к ^{+ y} j . к ^{A 1      -}

Далее, после получения на шаге t " _{+ 1} новых положений узлов лагранжевой сетки, методом поиска корня [17] в каждом элементе пересчитывались значения давления p и плотностей фаз р _g 1 , р l 1 согласно

Ро      а g 4р g 4 , а/ор/о             п п п уравнению сохранения массы смеси: — = —-—-—+--14 14 , где р/0, р 0, р0 — значения плотности р" рgi(p,Tg) р"i(p,T)                g4

жидкой, газовой фаз и смеси с шага, соответствующего времени t_n . Для вычисления величин давления и температуры для времени t " _{+ 1} применялся метод, разработанный В.Ф. Куропатенко [18]. Суть метода состоит в следующем: если разность скоростей в узлах текущей и соседней ячеек положительна, то в ячейке находится волна разрежения, и в этом случае температура и внутренняя энергия каждой фазы находится путем интегрирования условий адиабатичности [17]. При отрицательной разности скоростей состояние текущей ячейки соответствует состоянию области ударного сжатия; в таком случае используются соотношения Рэнкина-Гюгонио [17]. При решении задачи истечения пароводяной смеси с фазовыми переходами, как и в работе [9], также рассматривалась однотемпературная схема, когда для паровой составляющей принимается условие T_g = T l .

На следующем этапе расчетов определялись объемные содержания фаз:

"      -"

^р j , к    ^р l ( j , к ) )

^{( j , к} )     / "       _ "      \

^(Р g ( j , к )     ^Р l ( j , к ) )

^а I ( j , к )     ^{1    а} g ( j , к ) .

При учете парообразования проверялось наличие фазового перехода в перегретом состоянии и его интенсивность J_lg , в соответствии с (2), а также осуществлялся перерасчет массы каждой фазы, входящей в расчетную ячейку:

т "    = т11--l— \t ml (j,к) ml (j,к)      " A( ,

P j , к

"             "            lg— mg (j, к)    mg (j, к) +  " A t ,

P j , к

при этом общая масса смеси в ячейке оставалась с течением времени неизменной:

m jк = m ",к = m " (j,к ) ⁺ m g ( j , к ) .

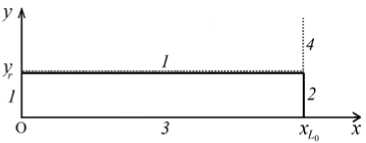
Рис. 2. Расчетная схема задачи: 1 , 4 – фиксированные границы, 2 – свободная граница, 3 – ось симметрии

При расчетах скорость вычислялась в узлах сетки; плотность, масса, объем и давление — в центрах ячеек. Для учета условий на свободных и фиксированных границах вводились «псевдоячейки» [16]. На оси Ox использовалось условие симметрии (Рис. 2). На границе x = 0 задавалось условие жесткой стенки, на границе x = xL^ — свободного вытекания, на боковой границе y = yr — условие скольжения. Для граничных ячеек, покидающих сосуд, то есть при x > xL^, принималось условие, что поверхность свободная. Для таких граничных ячеек, в зависимости от условий моделируемого эксперимента, дополнительно вводились внешние фиксированные границы.

В работе [19] была проведена проверка разработанной расчетной модели. Установлено удовлетворительное согласование численного решения тестовой задачи по двумерной осесимметричной модели в квазиодномерной постановке и аналитического автомодельного решения задачи исследования сильного взрыва газа в области цилиндрической конфигурации, полученного Л.И. Седовым [20]. Также был проведен сравнительный анализ численных решений на основе двухфазных моделей в двумерной осесимметричной постановке и решений аналогичных задач с использованием одномерных моделей в условиях плоской и цилиндрической симметрии.

3.    Постановка задачи и результаты численного моделирования

Численно моделировалась задача истечения вскипающей воды из цилиндрического сопла. Начальные и граничные условия формировались близкими к экспериментам, проведенным А.В. Решетниковым с соавторами [11]. В начальный момент времени вода в сосуде имела давление и температуру, соответствующие состоянию насыщения (Табл. 1). При удалении заслонки происходило вскипание и истечение пароводяной смеси из сопла радиусом y r = 0,0025 м и длиной x L^ = 0,15 м. Расчеты проводились на начальной нестационарной стадии процесса пространственного истечения. Начальное содержание паровой фазы принималось равным a g = 10 ^{- 5}.

Таблица 1. Экспериментальные [21] и вычисленные с использованием уравнения состояния [12] значения температур Т и плотностей воды рz и пара р g на линии насыщения и их относительные погрешности для начальных условий эксперимента [11]

p нэакссп , МПа	расчет    эксп 1 нас     ( p нас ) , K	эксп T нас  , K	8 Т , %	расчет    эксп Р l     ( p нас ) , кг/м3	эксп Р / , кг/м3	8 , , %	расчет    эксп р g    ( p нас ) , кг/м3	эксп p g , кг/м3	8 g , %
0,25	400,11	400	0,028	907,29	937,48	3,20	1,28	1,36	5,88
1,55	473,01	473	0,003	835,70	864,84	3,37	7,51	7,84	4,21
2,79	503,04	503	0,008	802,49	827,32	3,00	13,59	13,95	2,58
12,34	599,94	600	0,010	644,47	649,41	0,76	74,14	72,81	1,82

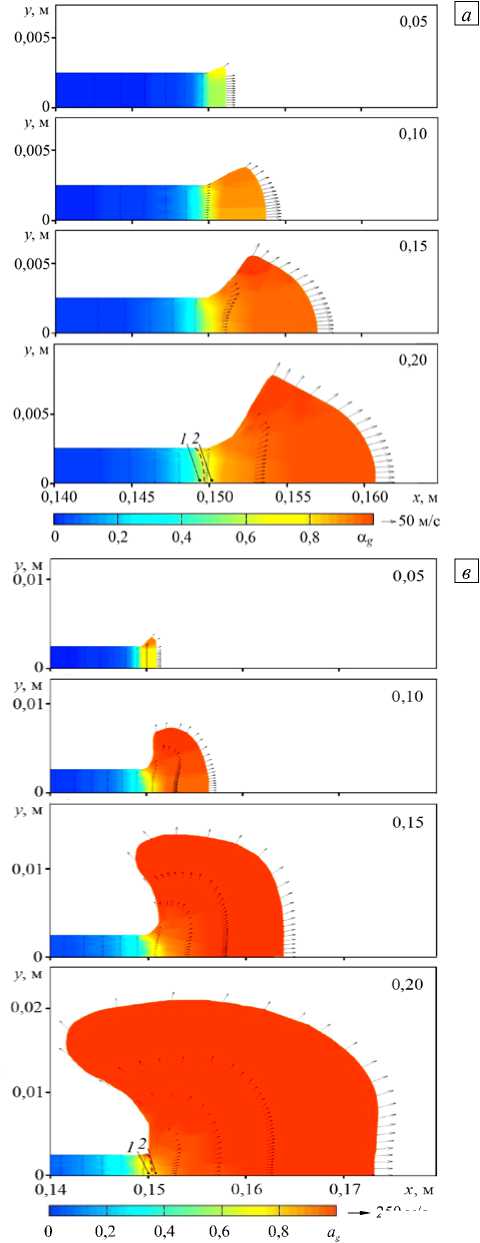
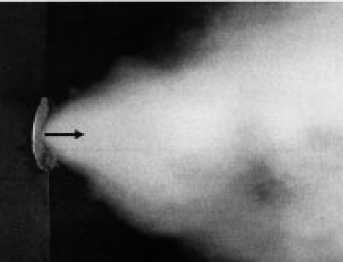
На рисунках 3, 4 для указанных в легендах моментов времени представлены результаты численного решения задачи в виде распределений объемного газосодержания a _g и полей скоростей v , полученные при различных начальных равновесных состояниях воды в сосуде (трубе) высокого давления (Табл. 1). Так, на рисунке 3 а решение соответствует начальному равновесному состоянию Т₀ = 400 K и p ₀ = 0,25 МПа . Вследствие разгерметизации внутрь трубы распространяется быстрая волна разгрузки, и начинается пространственное истечение вскипающего потока, в котором паросодержание a _g возрастает до 0,8. Наблюдается радиальное расширение струи за счет парообразования. С течением времени (см. фрагменты в моменты времени t = 0,1 + 0,2 мс) струя приобретает характерный конический вид. При увеличении начальной температуры и давления в состоянии насыщения до Т ₀ = 473 К и p ₀ = 1,55 МПа (Рис. 3 б ) струя вскипающей воды также имеет конический вид, а угол раскрытия, по сравнению с предыдущим вариантом (см. Рис. 3 а ), увеличивается от 40 до 80 градусов. На рисунке 3 г показана фотография струи вскипающей воды при рассматриваемой начальной температуре, полученная в экспериментах [11] при истечении из сосуда высокого давления через короткое цилиндрическое сопло с коническим углом распыла.

250 м/с

г

Рис. 3. Распределения объемного паросодержания a g и мгновенного поля скоростей v в процессе истечения в указанные моменты времени (мс) при различной начальной равновесной температуре T ₀ , K: 400 ( а ); 473 ( б ); 503 ( в ) и фотография из [11] струи вскипающей жидкости при Т о = 473 K ( г )

Расчеты показали, что дальнейшее повышение температуры до 480 К приводит к более интенсивному расширению паровой фазы и значительному увеличению скорости и дальности разлета частиц воды и пара формирующих струю, однако угол раскрытия струи не превышает 90 градусов. Этот результат согласуется с данными экспериментов из [11], в которых вплоть до указанных температур струя также имела конический вид с увеличением угла раскрытия при повышении начальной температуры. Дальнейшее повышение начальной равновесной температуры до То = 503 К, соответствующей давлению насыщения p0 = 2,79 МПа, в экспериментах [11] сопровождалось интенсивным вскипанием и расширением струи, приводящим к её развалу, с чем качественно согласуются данные расчетов для начальной стадии истечения, в которых струя закручивалась вдоль боковой поверхности трубы навстречу движению потока. На рисунке 3в, соответствующем начальным равновесным условиям Т0 = 503 K и p0 = 2,79 МПа, в моменты времени 0,15 и 0,2 мс видно начало закручивания струи.

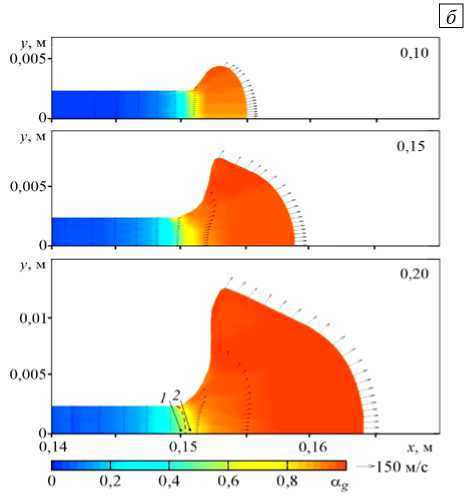
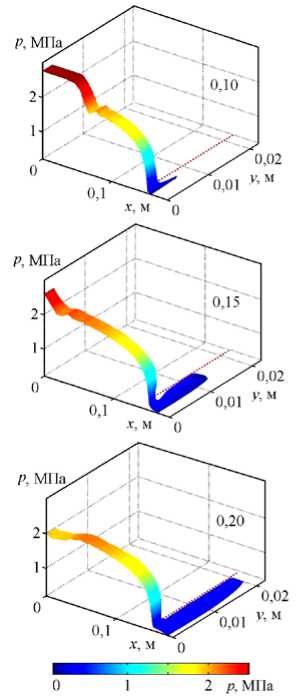
На рисунке 4 приведены результаты численного моделирования истечения вскипающей пароводяной смеси с учетом плоскости, перпендикулярной оси симметрии трубы и расположенной в плоскости среза выходного отверстия. Плоскость ограничивала движение формирующегося потока и растекание струи с углом раствора, равным 90 градусам, по аналогии с плоскостью за выходным срезом сопла

а

б

в

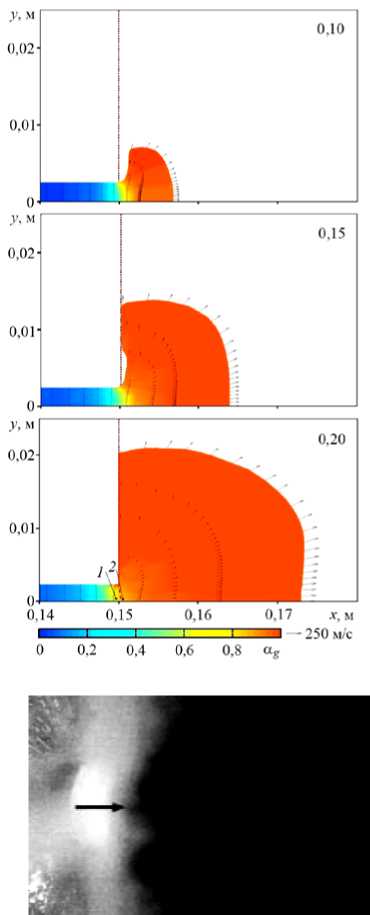
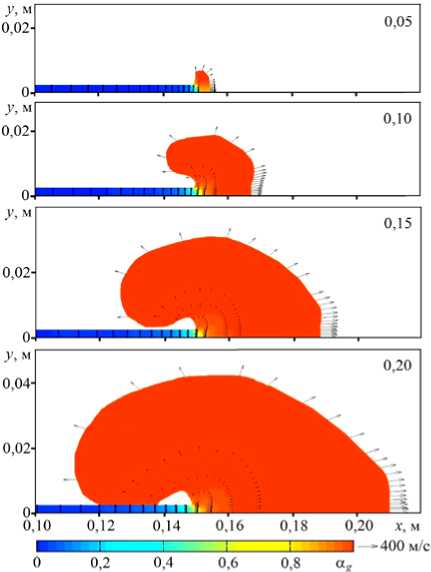
Рис. 4. Расчетные профили давления ( а ), распределения объемного паросодержания a _g и мгновенного поля скоростей v в процессе истечения в указанные моменты времени (мс) при начальной равновесной температуре Т о = 503 K ( а , б ) и Т о = 600 K ( в ); фотография струи вскипающей жидкости при Т = 503 K [11] ( г )

в экспериментах [11]. В расчетах роль плоскости выполняла внешняя фиксированная граница 4 (Рис. 2), на которой задавалось условие жесткой стенки. На фрагменте 4 б показаны распределения газосодержаний в обозначенные моменты времени. На фрагменте 4 а представлены расчетные профили давления для быстрой нестационарной стадии истечения моделируемого эксперимента ( Т₀ = 503 K, p ₀ = 2,79 МПа). После прохождения быстрой волны разгрузки, которая движется со скоростью около ~1000 м/с, внутри трубы устанавливается однородное давление ~ 2,1 МПа, что ниже значения, отвечающего состоянию насыщения. Из рисунка видно, что внутри трубы сохраняется одномерность течения, а в зоне свободной границы имеет место интенсивное высокоскоростное пространственное расширение струи за счет вскипания пароводяной смеси. На боковой границе трубы в зоне, прилежащей к свободной границе, в расчетах получено значение давления, более низкое по сравнению с осевым. На рисунке 4 г приведена взятая из работы [11] фотография экспериментальной струи вскипающей жидкости при начальной температуре насыщения Т ₀ = 503 K. Сравнительный анализ фотографии и результатов расчетов показывает их качественное согласование. Действительно, как в эксперименте, так и в расчетах на начальной нестационарной стадии истечения в присутствии плоскости, перпендикулярной оси сопла, наблюдается развал струи — растекание по боковой стенке с углом раскрытия 90 градусов.

При дальнейшем повышении начальной температуры до Т ₀ = 600 K, соответствующей условиям насыщения ( p ₀ = 12,57 МПа), в расчетах также получается развал струи (Рис. 4 в ), однако раскрытие струи происходит значительно быстрее, а именно в радиальном направлении смесь расширяется в два раза интенсивнее, чем в случае Т ₀ = 503 K (Рис. 4 г ). Рисунки свидетельствуют, что вскипающий поток формирует обширную паровую область, закручивающуюся навстречу его движению, и эта область, захватывая внешние границы трубы, растекается по ее поверхности (см. Рис. 4 в при t = 0,2 мс).

В настоящей работе исходя из значений числа Маха были выделены зоны дозвукового и сверхзвукового режимов начальной стадии истечения пароводяной смеси. Для определения местной скорости звука двухфазного потока в зависимости от газосодержания и давления использовалась методика, предложенная в работе [17].

На рисунке 3 в моменты времени t = 0,2 мс цифровые указатели 1 и 2 разграничивают области, соответственно, дозвуковых и сверхзвуковых режимов истечения вскипающей пароводяной смеси. В таблице 2 приведены значения скорости потока ( v x ), местной скорости звука ( c ), газосодержания ( a g ) и чисел Маха ( M ), найденные расчетным путем для начальных температур в областях течения, отмеченных соответствующими указателями 1 и 2 на рисунке 3.

Таблица 2. Значения чисел Маха ( M₁ ) и скоростей потока ( v ₁ ) внутри сосуда и на открытом участке ( M₂ , v ₂ ) при различных начальных температурах в момент времени t = 0,2 мс

T , К	v 1 , м/с	c 1 , м/с	a g 1	M1	v 2 , м/с	c 2 , м/с	a g 2	M2
400	12,35	33,20	0,36	0,37	33,40	33,00	0,83	1,01
473	15,40	36,12	0,38	0,43	35,60	33,80	0,84	1,05
503	26,11	41,23	0,42	0,64	48,40	39,80	0,86	1,20

Дозвуковой режим истечения реализуется внутри трубы (0 <  x <  x L^ ), где паросодержание потока не превышает a g <  0,45. Сверхзвуковое истечение формируется на открытом участке трубы ( x >  x L_o ), где a g >  0,5. При скорости потока, превышающей скорость волны разрежения, распространяющейся со скоростью звука, устанавливается режим «запирания», то есть вблизи оси симметрии трубы на участке истечения, непосредственно примыкающем к свободной границе, образуется и сохраняется высокий градиент давления (см. распределения объемного газосодержания на рисунках 3, 4), поддерживающийся интенсивным вскипанием и значительным ускорением движения вскипающей воды, вследствие чего волна разрежения сносится потоком и не попадает внутрь трубы. Дальнейшее увеличение паросодержания на рассматриваемом внешнем участке трубы соответствует завершающей стадии процесса истечения, когда скорость потока ослабевает, становится дозвуковой, и волна разрежения устремляется внутрь трубы. Более детальное исследование этой стадии процесса истечения вскипающей воды проведено в одномерном приближении в работе [9].

4.    Заключение

В настоящей работе предложено обобщение одномерной двухфазной модели парожидкостной смеси в условиях неравновесного вскипания [9] с использованием широкодиапазонного уравнения состояния воды и пара [12] на случай численного исследования задач, связанных с истечением вскипающей парожидкостной смеси при внезапной разгерметизации сосудов высокого давления в случае пространственной осевой симметрии задачи. Численная реализация модели проведена методом сквозного счета на основе подвижных лагранжевых сеток, модифицированным для расчета двухфазных парожидкостных смесей при наличии фазовых переходов.

Изучены особенности формирования струй вскипающей жидкости при различных равновесных начальных состояниях воды в сосуде высокого давления в условиях, приближенных к экспериментам, проведенным авторами [11]. Получены пространственные распределения давления, полей скоростей и паросодержания. Исследованы зоны образования дозвуковых и сверхзвуковых течений вскипающей пароводяной смеси. В расчетах установлено, что при начальных температурах состояния насыщения воды ниже 480 К струя имеет конический вид; дальнейшее повышение начальной температуры насыщения при приближении к критической точке приводит к закручиванию струи навстречу движению потока и формированию начальной стадии режима развала струи, что качественно согласуется с результатами экспериментов работы [11].

Работа выполнена при финансовой поддержке РФФИ (№ 14-01-97007-p_поволжье_а), Программы фонда фундаментальных исследований ОЭММПУ РАН (ОЭ-13) и Совета по грантам Президента РФ для ведущих научных школ (код проекта НШ-2669.2014.1).