Пространственные характеристики четырехволнового преобразователя излучения в многомодовом световоде с резонансной нелинейностью

Возможностью концентрации в световоде энергии взаимодействующих волн при одновременном увеличении длины взаимодействия позволяет значительно увеличить коэффициент отражения четырехволновых преобразователей излучения к> 1 + № 2 - № 3 = № 4 с использованием широкого класса лазерных источников, получить высокоэффективные малогабаритные нелинейные оптические устройства [1–5].

В экспериментах по изучению четырехволновых взаимодействий в световодах используются среды с различными механизмами нелинейности [6–8]. В средах с резонансным механизмом нелинейности за счет подбора частот взаимодействующих волн можно значительно увеличить нелинейную восприимчивость среды, а значит и коэффициент отражения четырехволновых преобразователей излучения [9–10]. Таким образом, для получения больших коэффициентов отражения практический интерес представляет изучение четырехволновых взаимодействий в световодах, заполненных средой с резонансной нелинейностью.

Кроме коэффициента отражения, еще одной важной характеристикой четырехволновых преобразователей излучения, используемых в системах обработки и распознавания образов, в системах адаптивной оптики, является качество преобразования, оцениваемое по соответствию комплексных амплитуд падающей (сигнальной) и отраженной (объектной) волн [11]. В приближении заданного поля по волнам накачки для определения качества преобразования при многоволновом взаимодействии широко используется метод функции размытия точки [12]. С использованием этого метода при малом коэффициенте отражения проанализированы пространственные и временные характеристики вырожденных четырехволновых преобразователей в световодах с керровской, тепловой нелинейностями [13–15].

В настоящей работе анализируется временная зависимость ФРТ четырехволнового преобразователя в многомодовом световоде с резонансной нелинейностью, исследуется влияние на вид ФРТ параметров световода, характеристик волн накачки. Считается, что сердцевина световода состоит из «матрицы» и ансамбля частиц, моделируемых трехуровневой системой энергетических уровней

1. Вывод выражения для амплитуды объектной волны

Пусть в двумерном световоде, расположенном между плоскостями z = 0 и z = L , распространя-

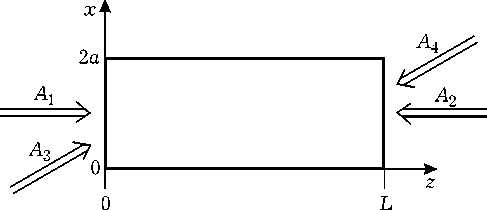
Рис. 1. Схема ЧВВ в световоде ются навстречу друг другу две волны накачки с комплексными амплитудами A1 и A2 и сигнальная волна с амплитудой A3 . В результате вырожденного четырехволнового взаимодействия to + to - to = to генерируется объектная волна с амплитудой A4 (рис. 1).

Исходное скалярное волновое уравнение, описывающее вырожденное четырехволновое взаимодействие, есть

[v² + к ² - 2 ik а] ( A + к . с . ) = 0.                   (1)

Здесь

A = S A j , к ^

j = 1

– волновое число, n ₀ – среднее значение показателя преломления, а — коэффициент поглощения, зависящий от интенсивности распространяющихся в среде волн.

Коэффициент поглощения излучения в световоде определяется коэффициентом поглощения «матрицы» ( а₀ ) и коэффициентом поглощения ансамбля частиц ( а 1 )

а = а о + а 1 .

Пусть один из энергетических уровней частицы является метастабильным. Метастабильное состояние, как правило, имеет триплетную природу. Кинетические уравнения, описывающие изменение заселенностей основного синглетного

( N 1 ) , возбужденных синглетного ( N 2 ) и триплетного ( N з ) уровней, имеют вид [16]

~1Т" = - N 1 1 ^ 12 + N 2 ⁽ I ^ 21 + § 21 ) + N 3 8 31 ,

‘ —Г = N 1 1^ст 12 ^- N 2 ⁽ I ° 21 ^{+ 8} 21 ^{+ 8} 23 ) ,          ⁽²⁾

N = N 1 + N ₂ + N 3 .

Здесь стij и 8ij — сечение поглощения (излучения) и вероятность безызлучательных переходов между i и j энергетическими уровнями, N – общая концентрация частиц. Коэффициент поглощения ансамбля частиц связан с заселенностями энергетических уровней выражением:

^а 1 = N 1 CT 12 ^- N 2 ^ст 21 .

В приближении заданного поля по первой волне накачки (| A 11 >>  A 2 3 4| ), при учете интерференции первой волны накачки и сигнальной волны распределение интенсивности можно записать следующим образом

I = AA * = I о + A 1 A 3 + A 1 * A 3 , (3) где I о = A 1 A p

Разложим комплексные амплитуды взаимодействующих волн по модам световода, не содержащего ансамбля частиц

N

A j = ^ a jn ( t , z ) f n ( x , z ) , j = 1 ^ ⁴ , (4) n = 0

где f n ( x , z ) = f n ( x ) exp ( - i P _n z ) — n -ая мода световода; P _n — постоянная распространения n -ой моды, N — число отсечки, a jn ( t , z ) — коэффициенты в разложении амплитуд волн по модам световода.

Учитывая изменение интенсивности (3), представим заселенности энергетических уровней в виде

N j ( x , z , t ) = N j о ( x , z , t ) +

^N                                                (5)

⁺ S ^N jP ( ^z , t ) ^f P ( ^x ) , j = ¹ " 3.

p = 0

Коэффициент поглощения ансамбля частиц можно представить в виде суммы быстро (а31 ) и медленно (аю ) меняющихся в зависимости от координат составляющих а1 = аю (x, z, t) + а31 (x, z, t).                      (6)

Здесь аю (x, z, t) = CT12 [N10 (x, z, t) - N20 (x, z, t)], (7) а31 (x, z, t) =

N

= ^CT 12 ^ [^ V 1 p ( ^z , t ) ^- NJ 2 p ( ^z , t ) ] ^f p ( ^x ) =           ⁽⁸⁾

P = 0

N

= ^ *аP ( z, t ) fP (x), p=0

NN 10 20 и аю — средние значения заселенностей энергетических уровней и коэффициента поглощения ансамбля частиц, N 1 p 2 p и (i p — коэффициенты в разложении заселенностей энергетических уровней и быстро осциллирующей в пространстве составляющей коэффициента поглощения ансамбля частиц по модам световода, (X p = ^ст 12 ( N 1 p ^— N 2 p ) .

С учетом (6) уравнение Гельмгольца (1) распадается на систему четырех уравнений	2. Определение коэффициентов в разложении по модам световода
[ ( v2 + k 2 - 2 ik a’ ) A m = 0, m = 1 ^ 3, f                                          (9) l ( v2 + k 2 - 2 ik a 0 ) A 4 - 2 ik a31 A 2 = 0,	быстро осциллирующей в пространстве составляющей коэффициента поглощения ансамбля частиц
где a 0 = a o + a^ В приближении медленно меняющихся амплитуд с учетом (3)–(5) система уравнений (9) примет вид da        da       da —n = 0, —2 m = 0, —— = 0, dz         dz        dz da 4 1 ( t , z ) _ < dz                                              (10) k N N = -Г Ё Ё a 2 m a P ( t ’ z )x P 1 m = 0 p = 0 xY mpl exP [- i ( P m -P 1 ) z ] -	Будем считать, что первая волна накачки одномодовая с номером моды n A 1 ( x , z , t ) = a 0 n ( t ) f n ( x ) exp ( - i в n z ) . После подстановки выражения для интенсивности (3) и заселенностей энергетических уровней (5) в систему уравнений (2) она распадается на две системы уравнений: для средних значений заселенности dN 10 ( x , z , t ) = dt = - N 10 ( x , z , t ) [ 1 0 ( x , z , t ) ” 12 +8 31 ] +
Здесь Y mpl = J f m ( x ) f p ( x ) f t ( x ) dx - интеграл перекрытия, определяющий эффективность взаимодействия трех мод световода. При выполнении граничных условий a 1 n ( t , z = 0 ) = a 0 n ( t ) , a 2 m ( t , z = L ) = a 0 m ( t ) ,                          (11) a 3 k ( t , z = 0 ) = a 0 k ( t ) , a 4 1 ( t , z = L ) = 0 найдем коэффициенты в разложении амплитуды объектной волны по модам световода на его передней грани a 4 1 ( t , z = 0 ) = k NN  L = -В" Ё! a 0 m J a p ( t , z ) x                (12) P1 m = 0 p = 0     0 x Y mp1 ex P [- i ( P m - P 1 ) z ] dz , а значит и амплитуду объектной волны A 4 ( x , z = 0, t ) = = - k ” 12 f x 1 = 0 e 1 NN   L                       (13) x ff a 2m J [ N 1 p ( z,t ) - N 2 p ( z,t ) ]x m = 0 p = 0     0 x Y mp1 ex P [- i ( P m - P 1 ) z ] dz - Амплитуда объектной волны однозначно определяется коэффициентами в разложении заселенностей энергетических уровней по мо-	< + N 20 ( x , z , t )[ I 0 ( x , z , t ) ” 21 + 8 21 - 8 31 ] + N 8 31 , dN n( x , z , t )         ,      x ,      x               (14) 1 = N 10 ( x , z , t ) I 0 ( x , z , t ) ” 12 dt -    N 20 ( x , z , t ) [ I 0 ( x , z , t ) ” 21 + 8 21 + 8 23 ] , _ N 10 + N 20 + N 30 = N , для коэффициентов в разложении заселенностей энергетических уровней по модам световода [ dN 1 p ( z , t ) dt      - N 1 p ( z , t )[ I np ( z , t ) ” 12 +8 31 ] + + NN 2 p ( z , t )[ I np ( z , t ) ” 21 + 8 21 - 8 31 ] + F p ( t , z ) , < dN „ ( z , t ) 2 dt      = 27 1 p ( z , t ) I np ( z , t ) ” 12 -             (15) -    NN 2 p ( z , t ) ( I np ( z ) ” 21 + 8 21 + 8 23 ) - F p ( t , z ) , _ N 1 p + N 2 p + N 3 p = 0- Здесь I 0 ( x , z , t ) = | a 0 n f u ( x ) f n ( x )e xp [- iz ( p n -P n ) ] , I np ( z , t ) = | a 1 n | Y nnpp exp [- iz ( p n - P n ) ] , Y nnpp = J I f n ( x )| I f p ( x )| dx , F p ( t , z ) = N = - f a 0 n ( t ) a0 k ( t ) ex P [- iz ( p n - P k ) ] x k = 0 x J a 10 ( x , z , t ) fu ( x ) f k ( x ) ~p ( x ) dx . Системы уравнений (14)–(15) дополняются на-

дам световода.

чальными условиями

N 10 ( x , Z , t = 0 ) = N ,

N 20 ( x , z , t = 0 ) = N 30 ( x , z , t = 0 ) = 0,

N 1 p ( z , t = 0 ) = N 2 p ( z , t = 0 ) =

= N 3 p ( z , t = 0 ) = 0.

D 1,2 p =

= ± ^X 2,1 ⁺ I np ^{( g} 12 ⁺ ° 21 ) ⁺ § 21 ⁺ § 23 ^X 1 ^{— X} 2

Решая систему уравнений (14) с учетом начальных условий (16), при неизменности во времени интенсивности первой волны накачки ( I о ( x , z , t ) = I о ( x , z ) ) , получим для средних значений заселенностей энергетических уровней следующие выражения

N 10 ( x , z , t )

^N § 31 [ I 0 ^CT 21 + § 21 + § 23 ] ^X 1 ^X 2

t x J Fp (t', z) exp (—X‘,21') dt'.

Выражение для X12 совпадает с выражением для X1 2 при замене Iо(x, z) на Inp(z)•

Подставив (18)–(19) в (7), а (20)–(21) в (8), найдем:

• среднее значение коэффициента поглощения ансамбля частиц

+

^{N [} I 0 « 12 + § 31 + ^X 2 ^](§ 31 + ^X 1 )

^X 1 ( ^X 2

^^^^^^B

X1)

exp ( X 1 t )

^^^^^^B

^{N [} I 0 « 12 +§ 31 ^{+ X} 1 ^](§ 31 ^{+ X} 2 )

^X 2 ^(X 2

^^^^^^B

X1 )

exp ( X 2 t ) ,

N 20 ( x,z,t ) = N § 31fei -^X 1 ^X 2

NI 0« 21( § 3r+^X1)

^X 1 ( ^X 2 ^{— X} 1 )

exp ( X 1 t )

+

• « 10 ( ^x , ^z , t ) = N ^y-⁺

• ^{1    + bI} 0

• ^N « 12 [ I 0 ⁽« 12 ⁺ « 21 ) ⁺ § 31 ^{+ X} 2 ]⁽§ 31 ^{+ X} 1 )

• +-----------------------------------------------x

• ^X 1 ( ^X 2 ^{— X} 1 )

x exp ( X 1 1 ) —                                     (22)

• _— ^N « 12 [ I 0 ⁽« 12 ⁺ « 21 ) ⁺ § 31 ^{+ X} 1 ]⁽§ 31 ^{+ X} 2 ) _x ^X 2 ( ^X 2 ^{— X} 1 )

x exp ( X 2 t ) ,

+ ^NI 0 « 21 ⁽§ 31 ^{+ X} 2 ) ^X 2 ^(X 2 ^{- X} 1 )

exp ( X 2 1 ) ,

• коэффициенты в разложении быстро осциллирующей в пространстве составляющей коэффициента поглощения ансамбля частиц по мо-

где

^X 1,2 ( ^x , ^z ) =

= [ I 0 ⁽« 12 ⁺ « 21 ) ⁺ § 21 ⁺ § 31 ⁺ § 23 ] ±

± [ [ I 0 ⁽« 12 ⁺ « 21 ) ⁺ § 21 ⁺ § 31 ⁺ § 23 ] _

" [                 4

^— I 0 ^[« 12 ⁽§ 23 ⁺ § 31 ) ⁺ « 21 § 31 ] ^—

—

§ 31 ⁽§ 21 ⁺ § 23 ) f .

дам световода

« p ( ^z , t ) =

N exp [^{— iz} ( ^e n ^— P k ) ]

^ = 0    ^X 1 ⁽ z ^{) —X} 2 ⁽ z )    ^x

t x J [B1 (z) exp {X1 (t — t')} +

+ B2 (z) exp {X2 (t — t')}] a0n (t') a3k (t') x x [ J «10 (x, z, t') fn (x) fk (x) fp (x) dx] dt'.

Зная средние значения заселенности энергетических уровней N ₁₀ и N ₂₀, можно, используя систему уравнений (15) и начальные условия (17), найти коэффициенты в разложении заселенности энергетических уровней по модам световода

NN 2 p ( ^z , t ) = D 1 p exp ( ^X 1 t ) ⁺ D 2 p exp ( ^X 2 t ) ,

^N 1 p ( z , t ) =

I np ^{( z} ) « 21 ⁺ § 21 ^— § 31

D 1 p exp ( ^X 1 t )

+

D 2 p exp ( X 2 1 ) ,

Здесь

B 1,2 ^{( z} ) =

= ±^[X 2,1 ^{( z} ) ⁺ I np ^{( z )(}« 12 ⁺ « 21 ) ⁺ § 21 ⁺ § 23 ] ^x

I       [ Inp (z) «21 + §21 — §31 ]«12 I x 1 «21 — t;—z x . т—rvz—t^— 1,

I         ^X 1,2 ^{( z} ) ⁺ I np ^{( z} ) « 12 ⁺ § 31

b = « 12 ⁽§ 23 ⁺ § 31 ) ⁺ « 21 § 31 § 31 ⁽§ 23 ⁺ § 21 )

Подставив (23) в (12), найдем коэффициенты в разложении амплитуды объектной волны по модам световода, а значит и саму амплитуду объектной волны на передней грани световода.

3. Функция размытия точки четырехволнового преобразователя излучения

Здесь

^S 1 ^{( z} ) ^—

f B l ^{( z} ) [X 1 ( z )

B 2 ( ^z ) I ^x 2 ( z ) J

Пусть сигнальная волна является волной от точечного источника, расположенного на передней грани световода,

A 3 ( t , x , z — 0 ) — 5 ( x - x о ) .

Функция размытия точки на передней грани четырехволнового преобразователя излучения в

x

N O 12 J

.f n ( ^x ) f l ( ^x ) . f p ( ^x ) dx 1 + bl 0 ( x , z )

световоде имеет вид

Г ( x , x о , z

-OtV-kyLlxl x

O, t k            x l—о в l

При записи (25) считали, что при совпадении номеров одномодовых волн накачки ( n — m ) каждой моде сигнальной волны соответствует мода объектной волны, номер которой совпадает с номером моды сигнальной волны ( k — l ) .

4. Обсуждение результатов

NNN

AAA f k ^{( x} 0 ) ^a 1n ^a 2m ^Y mpl ^x m — 0 k — 0 p — 0

x f exp ^{(- i A} "mk' z ) S ( z,t ) dz, 0 ^X 1 ⁽ z ^)-X 2 ⁽ z )

где

S ( z , t ) — J { B i ( z ) exp [X 1 ( t - t ' ) ] +

+ B2 (z) exp [X2 (t - t')]}x x [J «10 (x, z, t') fn (x) fk (x) fp (x) dx] dt,

Рассмотрим световод, ограниченный идеально проводящими поверхностями, параллельными оси Z и расположенными на расстоянии 2 а друг от друга. Будем считать, что « 0 >> « 1 , « 0 — const . Для такого световода

f n ( x ) — -z=sm q n x , a

в n — { k ² - 2 ik « 0 - q n } ²,

^A nmkl ^— P n ⁺ P m ^- P k ^- P l ^- волновая расстройка. Выражение (24) описывают временную динамику ФРТ четырехволнового преобразователя в световоде, заполненным ансамблем частиц, моделируемых трехуровневой схемой энергетических уровней.

В стационарном случае, когда обе волны на-

n( n + 1) где q n ^{—           [17]} .

2 a

Для мод, распространяющихся вблизи оси световода (приосевые моды k >>  q n ), постоянная распространения имеет вид

^в n ^— k ^- i ^a 0 ^- 2 k

П ( n + 1 ) ²

2 a

качки одномодовые с совпадающими номерами мод, выражение для ФРТ принимает вид

N f ,( x ) N_ .

Г1 (x, x0,z — 0) —-к^ —l    £ f (x0 )x l—0   в l   p—0

0 0_v    L ^{exp (-} i A nnll z )

^x a l n a 2 n ^Y npl                   s i ^{( z} ) ^dz .

0 Ы z ^)-^ 2 ^{( z} )

Характерный вид зависимости нормированного на наибольшее значение центрального максимума ( Г _max ) модуля ФРТ, расположенной на оси световода ( ^х 0 — а ) , от поперечной координаты, полученный при анализе выражения (25) с использованием (26)–(27), представлен на рис. 2. Зависимости, приведенные на этом и последующих рисунках, построены при условии, что в «длинном» световоде ( L Re ( A _nmkl ) >> 1 ) взаимодействуют волны с X — 0.53 мкм, среднее

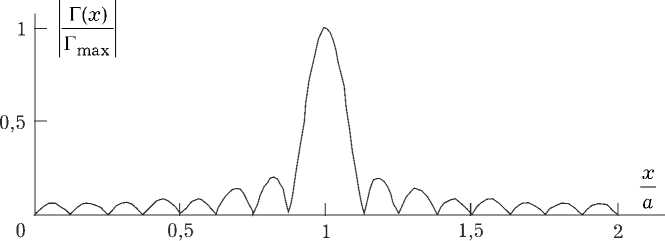
Рис. 2. Зависимость нормированного модуля ФРТ от поперечной координаты ( a — 10 мкм, N_c — 15, n — 0, bI_m — 4.64)

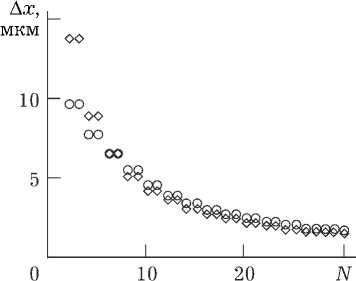
Рис. 3. Зависимость ширины центрального максимума ФРТ от числа приосевых мод ( a = 20 мкм, bI m = 0.185, n = 0 (ромбы), n = 4 (круги))

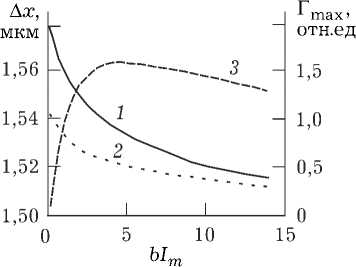
Рис. 5. Зависимость ширины 1 - 2 и величины центрального максимума 3 модуля ФРТ от нормированной интенсивности первой волны накачки ( n = 0; 1 — a = 10 мкм, N c = 15; 2 — a = 20 мкм, N c = 30)

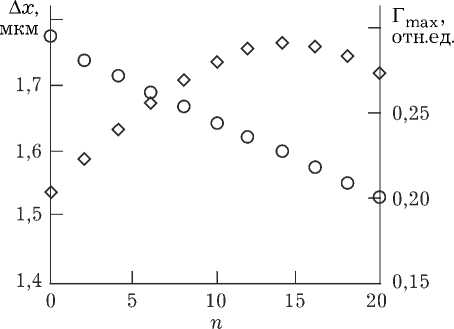
Рис. 4. Зависимость ширины центрального максимума модуля ФРТ (ромбы), наибольшего значения центрального максимума модуля ФРТ (круги) от четных номеров моды накачки ( a = 20 мкм, N_c = 30, bI m = 0.185)

значение показателя преломления сердцевины световода n o = 1.46, коэффициент поглощения «матрицы» а о = 0.1 см .

По мере увеличения поперечной координаты значение модуля ФРТ уменьшается, при этом наряду с центральным наблюдаются побочные максимумы, количество которых равно числу мод световода, участвующих в формировании амплитуды объектной волны.

Будем характеризовать качество преобразования излучения при четырехволновом взаимодействии в световоде шириной центрального максимума модуля ФРТ [13; 14]

A x = Х 2 - Х 1 , (28) где Х 1 и Х 2 определяются из условия Г( X 12 , x 0 , z = 0, t ) = 1 r m _ax( X o , t ). Ширина центрального максимума модуля ФРТ характеризует разрешающую способность четырехволнового преобразователя излучения.

Рассмотрим стационарный случай. Увеличение числа приосевых мод, дающих вклад в ФРТ, при фиксированной ширине световода приводит к уменьшению ширины центрального максиму- б)

\x, мкм

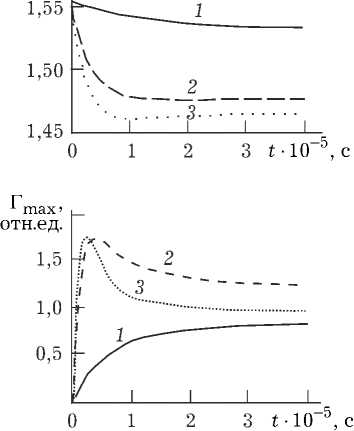
Рис. 6. Временная зависимость ширины центрального максимума ( а ) и наибольшего значения ( б ) центрального максимума модуля ФРТ ( n = 1, a = 5 мкм, N c = 7, 1 — bI m = 0.742;

2 — bI m = 11.28; 3 — bI m = 22.44)

ма модуля ФРТ с выходом на постоянное значение (рис. 3). Наибольшее значение центрального максимума модуля ФТР при этом возрастает. Таким образом, ширина модуля ФРТ полностью определяется приосевыми модами волновода, максимальное число которых находится из условия N _c — 0.1 N .

При условии n <  N _c /2 увеличение номера моды одномодовых волн накачки приводит к уменьшению по закону близкому к линейному наибольшего значения центрального максимума модуля ФРТ, при этом ширина центрального максимума модуля ФРТ вначале возрастает, а затем уменьшается (рис. 4).

С ростом интенсивности волны накачки ширина центрального максимума модуля ФРТ незначительно уменьшается (рис. 5), причем чем меньше ширина световода, тем это уменьшение заметнее. При этом наибольшее значение центрального максимума сначала резко возрастает, а затем медленно уменьшается, что является характерным для сред с резонансной нелинейностью [18–20]. Ширина световода не влияет на характер этой зависимости.

На рис. 6 приведены характерные графики временной зависимости ширины и наибольшего значения центрального максимума модуля ФРТ. При малых значениях интенсивности первой волны накачки (bI m <  1, I m — максимальное значение интенсивности волны накачки на передней грани световода) со временем ширина центрального максимума модуля ФРТ монотонно уменьшается, а наибольшее значение центрального максимума ФРТ монотонно увеличивается, выходя на постоянные значения. При значениях интенсивности bI m >  10 во временной зависимости ширины центрального максимума модуля ФРТ наблюдается минимум, а во временной зависимости наибольшего значения центрального максимума ФРТ – максимум, положения которых по мере роста интенсивности волны накачки сдвигаются в сторону меньших времен.

Заключение