Простые уроки сложности

* Физический факультет, Университет Иллинойса в Урбана-Шампейн, г. Урбана, США ** Физико-математический факультет, Университет Чикаго, Институт Джеймса Франка, г. Чикаго, США

Сложность мира контрастирует с простотой основных законов физики. В последние годы значительные исследования были посвящены системам, которые демонстрируют сложные результаты. Этот опыт не дал нам никаких новых законов физики, но вместо этого дал ряд уроков о приемлемых подходах к изучению сложных систем.

Обложка журнала Science (1999. V. 284, No. 5411), в котором опубликована статья

Найджела Гольденфельда и Льва Каданоффа.

Одним из самых ярких аспектов физики является простота её законов. Уравнения Максвелла, уравнение Шредингера и гамильтонова механика могут быть выражены несколькими строками. Идеи, которые составляют основу нашего мировосприятия, также очень просты: мир закономерен, и везде действуют одни и те

¹ Goldenfeld N.D., Kadanoff L.P. Simple lessons from complexity // Science. 1999. V. 284, No. 5411. P. 8789. (Пер. с англ. Г.С. Розенберга).

же основные законы. Все просто, аккуратно и описывается с точки зрения повседневной математики, либо дифференциальными уравнениями в частных производных, либо обыкновенными дифференциальными уравнениями.

Все просто и опрятно – кроме, конечно, самого мира (Everything is simple and neat – except, of course, the world).

В любом месте, где бы вы не находились – за пределами класса физики, – каждый видит мир удивительной сложности. Мир состоит из сложных «экологий» на всех уровнях, от огромных горных хребтов до тонких изгибов на поверхности песчаной дюны, от соленых брызг, порождающих волну, до взаимозависимостей финансовых рынков и до истинной экологии, созданной живыми организмами. Каждая ситуация высоко организована и своеобразна, а биологические системы образуют предельный случай исключительной сложности. Так почему же, если законы так просты, мир так сложен? Здесь мы попытаемся частично ответить на этот вопрос и суммировать, какие общие уроки можно извлечь из недавней работы над сложностью в физических системах.

Для нас сложность означает, что у нас есть структура с изменчивостью. Таким образом, живой организм является сложным, потому что он имеет много разных рабочих частей, каждая из которых образована вариациями в рамках одного и того же генетического кодирования. Один взгляд на океан или небо убеждает нас, что в физическом мире существует некоторая естественная тенденция к формированию структуры. Хаос также встречается очень и очень часто. Хаос – это весьма чувствительная зависимость конечного результата от начальных условий, которые его вызывают. В хаотическом мире трудно предсказать, какие измене-33

ния возникнут (произойдут) в данном месте и времени. На самом деле ошибки и неопределенности часто растут экспоненциально со временем. Сложный мир интересен, потому что он очень структурирован. Хаотичный мир интересен, потому что мы не знаем, что будет дальше. Но в мире есть и закономерности. Например, климат очень сложен, но зима следует за летом по достаточно предсказуемой схеме. Наш мир сложен и хаотичен. Далее следует элементарный урок:

Природа может создавать сложные структуры, даже в простых ситуациях, и некоторые простые законы, даже в сложных ситуациях .

СОЗДАНИЕ СЛОЖНОСТИ

Жидкости часто демонстрируют сложное поведение, которое может быть либо высокоорганизованным (например, торнадо), либо хаотичным (например, сильно турбулентный поток). То, что часто наблюдается, зависит от размера наблюдателя. Муха, попавшая в торнадо, с удивлением узнаёт, что он участвует в высоко структурированном потоке.

Уравнения, которые описывают, как скорость жидкости в одной точке пространства влияет на скорость в других точках пространства, базируются на трех основных идеях.

Первое: местонахождение ( локализация ). Жидкость содержит много движущихся частиц. На каждую частицу влияют только те другие частицы, которые находятся в её непосредственной близости.

Второе: сохранение . Некоторые вещи никогда не теряются, только перемещаются, такие как частицы и импульс.

Третье: симметрия . Жидкость изотропна и вращательно инвариантна.

Чтобы создать компьютерную модель жидкости [1], представим некий танец (кадриль – square dance), в котором частицы движутся, подчиняясь трем основным идеям. В простейшем случае танец выполняется на правильной гексагональной решетке. Смотрите верхнюю панель рис. 1. Каждая частица характеризуется положением решетки и одним из шести направлений движения. Эти стрелки являются векторами импульса. Кадриль начинается с выхода на PROMENADE, что означает один шаг в направлении вашей стрелки. Результат показан на средней панели рисунка. И тогда [на следующем шаге] один из партнеров начинает SWING YOUR PARTNER (раскручивать, вертеть своего партнера), на что указывают вам поворот всех стрелок на данном сайте на шестьдесят градусов, если они суммируют суммарный импульс до нуля; результат показан на нижней панели рисунка. И номер частицы, и импульс сохраняются на каждом шаге. Если взять тысячи частиц и сделать тысячи шагов (в среднем, это немного), то это позволит сгладить данные. Мы получим картину движения, идентичную движению жидкости. Кадриль в этом случае ведет себя как жидкость просто потому, что шаги танца подчиняются трем основным законам движения жидкости [2].

Постепенно, благодаря таким примерам, мы поняли, что очень простые «посылки» могут давать очень красивые, богатые и структурированные результаты. Таким образом, наши танцоры своими простыми проходами и вращениями создали прекрасный мир движущихся жидкостей. Чтобы простые элементарные события могли создавать шаблонные и сложные выходные данные, нам требуется много повторностей. Наш пример включал много событий, потому что у нас было много «танцоров» и много времени.

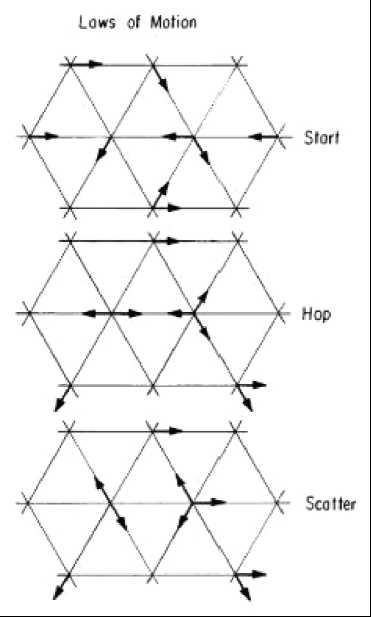
Рис. 1. Три этапа в алгоритме модели решеточного газа. Между верхней панелью и средней панелью каждая частица движется в направлении своей стрелки, чтобы попасть в ближайший соседний участок. Затем частицы «сталкиваются» всякий раз, когда суммарный импульс на сайте равен нулю. Эти столкновения происходят между средней и нижней панелями.

(Laws of Motion – законы движения, Start – начало, Hop – танец, Scatter – рассеивание).

Физиков восхищает, но не удивляет тот факт, что компьютер генерирует реалистичное плавное поведение, независимо от точных деталей того, как мы выполняем кодирование. Ибо, если бы это было не так, то мы были бы чрезвычайно чувствительны к микроскопическому моделированию – что можно условно назвать модельным хаосом – и физика, как наука не могла бы существовать: чтобы смоделировать бульдозер, нам нужно было бы осторожно моделировать составляющие его кварки! Природа оказалась настолько любезной, что предоставила нам удобное разделение масштабов длины, энергии и времени, что позволило вывести физические законы из четко определенных «слоев», даже если последствия этих законов очень сложны. Но нам не так повезло со сложностью в биологических или экономических ситуациях.

ПОНИМАНИЕ СЛОЖНОСТИ

Чтобы извлечь физические знания из сложной системы, нужно сосредоточиться на правильном уровне описания. Существует три способа исследования таких систем: экспериментальный, вычислительный и теоретический. Эксперимент лучше всего подходит для исследования, поскольку экспериментальные методы в сочетании с человеческим глазом могут очень эффективно сканировать большие диапазоны данных.

Компьютерное моделирование часто используется для проверки нашего понимания конкретного физического процесса или ситуации. В нашем примере с динамикой жидкости, крупномасштабная структура не зависит от подробного описания движения в малых масштабах. Мы можем использовать этот тип «универсальности», разработав наиболее удобную «минимальную модель». Например, большинство программ потока жидкости не должно моделироваться с помощью моделирования молекулярной динамики. Это моделирование настолько медленное, что, возможно, оно не сможет достичь режима, который позволит нам безопасно экстраполировать [результат] на большие системы. Таким образом, мы можем получить неправильный ответ. Вместо этого мы должны моделировать на макроуровне, использовать большие временные шаги, большие системы. Например, некоторые вычислительные биологи пытаются смоделировать динамику белка, следя за каждой маленькой частью молекулы. Результат: Большинство компьютерных циклов тратится на наблюдение за маленькими группами СН, шевелящимися взад и впе- ред. Ничего биологически значимого не происходит за то время моделирования, которое они могут себе позволить.

Используйте правильный уровень описания, чтобы «поймать» интересующие вас явления. Для описания бульдозера излишне использовать кварки.

Этот урок с равной силой применим к теоретической работе, направленной на понимание сложных систем. Моделирование сложных систем с помощью гибких схем замыкания или скрытых сложных теорий свободного поля не работает. Это может привести к успешному описанию мелкомасштабной структуры, но это описание, вероятно, не будет иметь отношения к крупномасштабным особенностям. Чтобы получить эти грубые признаки, чаще всего следует использовать более феноменологическое и агрегированное описание, направленное конкретно на более высокий уровень. Таким образом, финансовые рынки не должны моделироваться простым геометрическим броуновским движением, основанным на моделях, которые сегодня составляют основу современного подхода к производным рынкам. Эти модели были созданы, чтобы быть аналитически управляемыми и происходить из очень грубого феноменологического моделирования. Они не могут воспроизвести наблюдаемые сильно негауссовские распределения вероятностей на многих рынках, которые демонстрируют такую особенность, что у нее даже есть причудливое название – «толстые хвосты – fat tails». Вместо этого моделирование должно основываться на вопросе, какие простейшие нелинейности или нелокальности должны присутствовать, чтобы отделить функции универсального масштабирования от особенностей рынка. Включение слишком большого количества процессов и параметров затеняет желаемое качественное понимание.

Так что каждая хорошая модель начинается с вопроса. Разработчик должен выбрать правильный уровень детализации, чтобы ответить на поставленный вопрос.

СЛОЖНОСТЬ И СТАТИСТИКА

По мере движения жидкости она может нести некоторые «пассивные» элементы, которые сами по себе не влияют на поток. И энергия, и плотность примесей подвергаются такому движению, при котором они конвекционны (идут с потоком) и диффундируют (движутся случайно). Конвективное движение имеет тенденцию перемещать первоначально удаленные области жидкости близко друг к другу и, таким образом, создавать улучшенные градиенты.

Диффузия имеет тенденцию сглаживать градиенты.

Во многих ситуациях эти «пассивные скаляры» сопровождаются быстрым и турбулентным потоком, так что конвективное перемешивание имеет тенденцию доминировать над диффузией. Компьютерное моделирование и эксперименты показывают, что плотность скаляра вскоре формирует профиль, в котором есть много плоских областей, окруженных резкими скачками. Плоские области создаются комбинированными эффектами конвекции и диффузии в хорошо смешанных областях образца. Однако, поскольку плотность в целом должна следовать начальному градиенту, смешанные области должны быть разделены скачками.

Такое поведение, при котором в системе доминируют действительно большие события, называется прерывистостью . Перемежаемость, кажется, является повсеместной особенностью динамических систем. Погода внезапно становится штормовой. Есть ледниковые периоды. Обвал фондового рынка. Вспышки чумы. Самолет сталкивается с турбулентностью. В любом случае, поведение динамической системы имеет большой скачок, и этот скачок может иметь большие человеческие последствия.

Количественно оценивая эти вездесущие скачки, можно обнаружить, что они бывают разных размеров, причем, большие прыжки менее вероятны. Опытным путем размер скачков часто определяется распределением вероятностей, которое для больших скачков принимает вид:

1 I jump I

( jump ) =     exp( - ^jump ),    (1)

2σ     σ где σ – стандартное отклонение [3]. Сравним

(1) с обычной формулой Гаусса:

1           ( jump )²

P ( jump ) = (2 πσ ) 1/2 exp( - 2 σ 2 ), (2)

что является обычным предположением в статистических задачах со времен Гальтона. Хаотические и турбулентные системы часто демонстрируют экспоненциальное поведение, например (1). Невероятные (очень плохие!) события гораздо вероятнее с экспоненциальной формой, чем с гауссовой формой (2). Например, 6-секундное событие имеет вероятность 10-9 в гауссовском случае, в то время как с экспоненциальной вероятностью – 0,0025. Оценки, особенно оценки Гаусса, сформированные короткими временными рядами, дадут совершен- но неверную картину крупномасштабных колебаний. Эти соображения имеют важные последствия на финансовых рынках, как недавно подчеркнул Мандельброт [4]. Таким образом, мы подходим к очередному уроку:

Сложные системы образуют структуры, и эти структуры сильно различаются по размеру и продолжительности. Их вероятностные распределения редко бывают нормальными, так что исключительные события не так уж редки.

РАЗВИТИЕ СЛОЖНОСТИ

Давным-давно Качальский [5] и Пригожин [6] описали образование сложных структур в неравновесных системах. Их «диссипативные структуры» могут иметь некоторую сложность, которая может быстро расти со временем. Считается, что сравнительно сложные структуры не существуют в равновесии. А. Тьюринг [7] описал механизм, включающий уравнения диффузионной реакции, для развития организации в живых существах. Как мы видели из приведенных здесь примеров и многих других, в неравновесных ситуациях многоэлементные системы действительно могут быть очень сложными [8].

Вполне вероятно, что эта тенденция является основой жизни. Ограниченная версия этой идеи дана в «Самоорганизованной критичности» Бака, Тана и Визенфельда [9]. В эссе под названием «Больше – это другое», Андерсон [10] описал, как особенности организации могут появляться как «возникающее» свойство систем. Примером этой точки зрения является работа по сложным «фазовым переходам» и сопутствующие предположения о том, что различные аспекты биологических систем находятся в критической точке, между порядком и сложностью [11].

Следующие несколько лет, вероятно, приведут к дальнейшему изучению сложности в контексте статистической динамики с целью лучшего понимания физических, экономических, социальных и особенно биологических систем. Это будет захватывающее время. По мере того как наука «осваивает» сложность, нужно понимать, что сложность требует совершенно иных подходов, чем те, которые ранее были в физике. До сих пор физики искали фундаментальные законы, истинные для всех времен и мест. Но каждая сложная система отличается. По-видимому, нет общих законов для сложности. Вместо этого нужно найти «уроки», которые можно с пониманием усвоить в одной системе и применить к другой. Возможно, физика станет больше похожа на человеческий опыт.

NG подтверждает частичную поддержку Национального научного фонда через грант NSF-DMR-93-14938. LPK подтверждает частичную поддержку со стороны ASCI Flash Center в Чикагском университете по контракту DOE B341495 [12].