Простые возмущения базисов в пространствах кёте

Уже с давних пор вместе с классическими каноническими базисами функциональных пространств рассматривались «близкие», в некотором смысле, базисы типа Пинкерле и др. Построение таких «близких» систем (возмущений) использует либо спектральные свойства риссовских операторов, либо непосредственно ряд Неймана для обратного оператора.

Для решения важных задач структурной теории пространств К¨ете числовых последовательностей (например, решения проблемы единственности безусловных базисов) требуются оценки характеристик коэффициентных функционалов аналогичных возмущений базисов в этих пространствах.

Ниже, после некоторой модификации и обобщения известных результатов (см., например, [1–3]) о возмущениях базисных систем, внимание будет сосредоточено на конечномерных возмущениях p-абсолютных базисов пространств К¨ете в непосредственной связи с характеризацией всех базисов этих пространств.

1.    Возмущения базисов в пространствах последовательностей

Определение 1. Базис (e n ) счетно-нормированного пространства (E, ( | • | r ) Г =1 ) называют p-абсолютным (1 6 p <  го ), если система полунорм

∞                1p kekr = 1>0,(е)|рЫР   , r =1,2,...,

\ n=1            /

∞ где e = ^еП(е)еп, n=1

e G E, задает на E исходную топологию, т. е. системы полунорм ( | • | r ) Г =1 и ( к • k r ) Г =1 — эквивалентны.

В нормированных пространствах l p , 1 < p <  го , с p-абсолютным базисом ортов можно рассматривать операторы T : l p ^ l p , удовлетворяющие условию

∞

Е k Te n k q < + го , p + q = 1,

где en = (^in)^! — базис ортов. Вместо (en) можно брать и какой-нибудь другой p-абсолютный нормированный базис с тем же значением p. Такие операторы аналогичны операторам Гильберта — Шмидта и совпадают с ними при p = 2. При p = 1 можно рассматривать вместо (1) условие lim ||Tenk = 0, lim kTxnk = 0 n→∞           n→∞ kxn k для базиса (xn) с произвольными нормами элементов.

При выполнении каждого из этих условий в соответствующих пространствах проверяется без труда известный критерий предкомпактности образа единичного шара для банаховых пространств l p (p <  го ) числовых последовательностей. В самом деле, ограниченность образа T U единичного шара и равномерное убывание остатков показывается выкладкой с применением неравенства Гельдера (или непосредственно при p = 1)

T

∞

E n=N

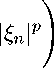
sup n ⁰ : k n ⁰ k lp = 1

1 ^p

∞ e n = N

ξ _n e _n

l p

sup n^lMllq = 1

∞

E ^П*(Te n )

n = N

∞

E

n = N

I n ⁰ (Te n ) | ^q

6 k ξ k l p

∞ kTenklqp n=N

для любых £ G l _p и N = 1, 2,... Согласно спектральной теории компактных операторов в банаховых пространствах, оператор I - T (I — тождественный) непрерывно обратим, если единица не является собственным числом оператора T , с описанным выше свойством (см., например, [4]).

Принимая во внимание эти факты, переходим к рассмотрению возмущений базисов в счетно-нормированных пространствах с p-абсолютными базисами.

Напомним, что пространством Кете,  определяемым матрицей  [a r (n)],

0 6 ar (n) 6 ar+i(n), r,n G N, называют пространство числовых последовательностей lp[ar(n)] = Ь = «n): I€|r = (i^ №(n) p \n=1          /

< + го , V r G N ,

где 1 6 p 6 го , и при p = го

|^|r = sup |£n|ar(n) < +го, Vr G N, n с топологией, определяемой монотонной системой полунорм (| • |r).

Базис ортов (e _n = (d _in ) i =₁ ) n =₁ пространства Кете, очевидно, является p-абсолютным базисом. В следующем утверждении речь пойдет о возмущениях базиса ортов, вместо которого можно брать и любой другой p-абсолютный базис этого пространства.

Предложение 1. Пусть последовательность элементов (g _n ) n =1 пространства Кете E = l p [a r (n)] (1 6 p <  го ) такова, что при любом r Е N для нее справедливо условие

Е ( l e n - g n i r V < . го ( lim '    '   = 0 при p =1 ) ,           (2)

П=1 V lenlr /               V" 'x lenlr                       / и нет нетривиальных разложений нуля по этой последовательности, т. е.

X Пп9п = 0 влечет Пп = 0, V n Е N, n то (gn )П=1 является p-абсолютным базисом пространства E, эквивалентным базису ортов, т. е. существует автоморфизм S пространства E, переводящий базис (en)n=1 в (gn)n=1.

C Определим сначала формально оператор S , полагая

∞∞

S€ = ^^ n g n для € = ^€ n e _n . n =1                n =1

Чтобы показать непрерывность S = (S — I ) + I , достаточно убедиться в непрерывности S - I . Для любого r ∈ N имеем

∞

| S^{€ —} £ | r = sup | ^€ 0 ⁽S^{€ — €)} | = sup X £ „ ^{€ 0 (}g n ^— e n ) l € 0 i r =1                      1С1 Г =1 n =1

6 (e ^c)) p _£s up, (e P0 () | q ) q 6    (e ( e ) q ) q .

n =1                  | s | r     \n=1                                 \n = 1

Применив те же рассуждения, что относились к операторам в банаховых пространствах l p и приведены выше, делаем заключение о компактности оператора A = S — I в каждом ассоциированном банаховом пространстве E _r , которое получается пополнением фактор-пространства E/N _r по норме | • | _r , где N r = { e Е E : | e | _r = 0 } .

Согласно условию предложения об отсутствии нетривиальных разложений нуля по системе (g _n ) П =1 , число 0 не является собственным значением оператора S. Поэтому оператор S = I + A имеет непрерывный обратный S ^-1 в каждом ассоциированном банаховом пространстве E r , r ∈ N (см., например, [4]).

Подставляя в определении S орты, т. е. полагая € = e _n , n = 1,2,..., видим, что

Se n = g n , а значит S ^{- 1} g _n = e n , n Е N. B

Замечание. При p = 1 вместо условия (2) в скобках можно использовать другое условие, обеспечивающее компактность описанного выше оператора A = S — I :

X sup ’ e n ^i e i l i < . го (Ae i = g i — e i ), V r Е N.

i      a. (i)

=

2.    Простые возмущения и вопросы единственности безусловных базисов в пространствах К¨ете

Напомним, что базис (e n ) n =₁ линейного топологического пространства E называют безусловным , если разложение каждого элемента сходится к этому элементу при любой перестановке членов.

В пространствах Кете E = l p [a r (n)] с p = 1, 2, го путем указания свойств определяющих матриц Кете [a r (n)] выделены классы, в каждом пространстве которых любой безусловный базис может быть получен из канонического (p-абсолютного) базиса ортов путем перестановки, умножения на числа, отличные от нуля, и автоморфизма пространства (см., например, [5, 6] и библ. в них). Если каждый безусловный базис данного пространства К¨ете E может быть получен из базиса ортов комбинацией указанных операций, то говорят о единственности безусловного базиса в E . Понятно, что в случае единственности безусловного базиса в E , любые два безусловных базиса переводятся друг в друга указанными операциями, и это называют свойством квазиэквивалентности всех безусловных базисов.

Согласно теореме Дынина — Митягина, в ядерном пространстве К¨ете — Фреше все базисы абсолютны (безусловны), а поэтому для указанных ядерных пространств ставилась проблема единственности базисов (свойства квазиэквивалентности всех базисов), которая решена пока только в частных случаях (см., например, [5, 6]).

В непосредственной связи с упомянутыми проблемами дадим для пары p-абсолютных базисов пространства Фреше достаточное условие их квазиэквивалентности в терминах свойств конечномерных возмущений специального вида.

Элемент f пространства Фреше (E, (| • |r)r=i) назовем выступающим (выступом) по отношению к данной системе полунорм (Hr)r=i, если существует непрерывный линейный функционал f0 Е E такой, что f0(fo) > 1 и |f0(e)||fo|r 6 |e|r+i, e Е E, r = 1, 2,...

Понятно, что для выступающего элемента f o соответствующий функционал f имеет оценки норм

| f 0 | r +i 6 Ж, r = 1, 2,...

В силу равностепенной непрерывности базисов в пространствах Фреше (см., например, [7]) для любого базиса или базиса дополняемого подпространства такого пространства можно выбрать систему полунорм ( | • | _r ) r =i , определяющую исходную топологию, таким образом, что каждый элемент базиса будет выступающим (выступом).

Можно показать для одиночного элемента пространства Фреше возможность выбора функционала и системы полунорм, задающей исходную топологию, таких, что этот элемент будет выступающим по отношению к выбранной системе полунорм.

Оценки норм функционала в определении выступающего элемента характеризуют геометрическое расположение (наклоны) этого элемента по отношению к некоторому гиперподпространству (множеству нулей соответствующего функционала).

Пусть теперь имеется в пространстве Кете — Фреше E = l p [a _r (n)] какой-нибудь базис (f m ) m ₌i (или базис дополняемого подпространства). Тогда только пользуясь равностепенной непрерывностью базиса (f m ) “ =i , путем разрежения системы полунорм пространства К¨ете E и умножения оставшихся полунорм на подходящие числа с изменением нумерации, можно добиться выполнения следующих условий:

• 1)    | e | r 6 r r | e | r +i , e Е E, r Е N;

• ²⁾    \ ^f m ^(e)||f m | r ^{6 |e|} r +i , e ^Е E, ^{r Е} N.

Лемма (ср. [5, 6]) . Пусть в пространстве Кете E = l _p [a _r (n)] (1 6 p 6 го ) система полунорм ( |^| _r ) , задающая топологию, удовлетворяет условиям 1) - 2) , и f 0 — выступающий элемент по отношению к этой системе полунорм с соответствующим функционалом f 0 .

Тогда существует натуральный индекс io G N такой, чтоei(o)(fo) = 0(f(ei(g)) = 0) и ar(i(0)) •Ifols    6 1

∀ r, s ∈ N.

^|f o | r +1 • a s +i (i(0)) 6 ’

C Рассмотрим случай p = 1, а остальные случаи рассматриваются аналогично как в [5].

В следующих неравенствах сначала используется условие 1), а затем тот факт, что f o (f o ) >  0 и справедливы соответствующие оценки определения выступающего элемента

∞   ∞∞

Е \ei(fo)l suP .     6 1 6 E If I If(ei)| 6 E КШ| inf + i=1         r f^1       i=1                  i=1         s |foI

Поэтому найдется натуральный индекс i(0) такой, что =i(fo) = 0, и ar(i(0))    . , as+1(i(0))

.

^suP Т7|--- 6 inf — --- r I f o I _r +1        s       I f o I _s

Можно считать одновременно f o (e i (o) ) = 0, так как в предыдущих оценках справа можно оценивать только члены числового ряда для f o (f o ), отличные от нуля. B

Отметим, что модификации рассуждений доказательства леммы использовались в [5, 6] (см. также [7]) для получения утверждений о единственности безусловных (p-абсолютных) базисов в широких классах пространств К¨ете. В доказательствах этих утверждений существенную роль играли комбинаторные соображения, известные как теоремы о системах различных представителей конечных или бесконечных наборов множеств [8]. Именно такой факт под названием теоремы Холла — К¨енига в исследовании вопроса о единственности безусловного базиса применялся в [9].

Поясним, о какой системе различных представителей идет речь.

Пусть в пространстве Кете E = l _p [a r (n)] рассматривается p-абсолютный базис (или p-абсолютный базис дополняемого подпространства) (f m ) ^ =_P Как уже отмечалось выше, систему полунорм, задающую топологию, всегда можно предполагать выбранной так, что выполняются неравенства

| e | r 6

∞

X

m =1

( I f m (e) ll f m l r ) p

= k e k r ⁶ 2 r ^|e| r +1 ,

e ∈ E, r ∈ N.

В случае, когда (f _m ) “ =1 — базис дополняемого подпространства F в E , выбирается непрерывный линейный проектор Q из E на F и система полунорм ( | • | _r ) Г =1 , задающая исходную топологию пространства E , строится таким образом, чтобы выполнялись неравенства

| Q^e| r ⁶ 2 r

∞                      ¹ p

Е Ifm,(Qe)|pIfmIP+1    6 227+11 = ^+2- m=1

e ∈ E, r ∈ N.

Тогда каждый элемент f _m будет выступающим по отношению к системе полунорм

( | • | _r ) Г =1 также, как и каждый элемент e _n .

Согласно утверждению леммы, для каждого элемента f _m

такой, что

найдется элемент e _n ( _m )

^|e n ( m ) | r ^|f m | s

^|e n ( m ) | s +1 ^|f m | r +1

6 1,

∀ r, s ∈ N.

Обозначив

λ _m

= inf s

| e n ( m ) | s +1 | f _m | _s

то же самое можно записать в виде двусторонних оценок полунорм элементов | e n ( m ) I r 6 ^ m I f m I r +1 6 | e n ( m ) | r +2 , V m,r G N, которые при дополнительном условии взаимной однозначности отображения m ^ n(m), m G N означают квазиэквивалентность p-абсолютного базиса (f _m ) “ =i части (e _n ( _m ) ) m =i базиса ортов. Зафиксируем некоторый натуральный индекс r(0) >  1 и для каждого m G N определим множество

| e _n | _r | f _m | _s

∀ r, s ∈ N .

^v r (0) ^(m) = n ^{G N :} I—I----- ^{6 1}

I              | e n | r + r (0) ^|f m | s + r (0)

Кроме того, v _r (o) (m) = 0, при любом m G N, так как r(0) >  1.

Если будет показано, что существует система различных представителей n(m) G v _r (o) (m), m = 1,2,..., n(m ₁ ) = n(m ₂ ), V m ₁ = m ₂ , то тем самым будет доказана квазиэквивалентность p-абсолютного базиса (f _m ) “ =i части базиса ортов. В этом случае при r(0) > 1 соответствующие двусторонние неравенства имеют вид

^|e n ( m ) | r ⁶ ^ m ^|f m | r + r (0) ^{6 |e} n ( m ) | r +2 r (0) , ^{V m} ,r ^{G N}-

Обозначим для произвольного конечного множества ^ = {mi, i = 1, 2,..., j} индексов базиса (fm)m=i множество j vr(0)(M) = IJ Vr(0)(mi) i=i индексов базиса ортов, и |A| ниже будет означать число элементов во множестве A, если оно конечно, и символ ∞, когда A бесконечно.

Простое необходимое и достаточное условие существования упомянутой выше системы различных представителей множеств v _r (0) (m) состоит в том, что для каждого конечного множества ^ = { m i , i = 1, 2,..., j } в соответствующем множестве v _r (0) (^) должно быть не менее j элементов, т. е.

Ы = j ^{6 |v} r (0) ⁽M^)|.

(Доказательство см., например, в [8] и применение — в [9]).

Легко привести крайние случаи «густых» и «разреженных» пространств К¨ете, когда условие (5) проверяется без труда.

Блочным пространством К¨ете называют пространство последовательностей векторов lp ([ar(n)],lk(n)) = {x = (xn), xn G lk(n), ^X kxnkppap(n)j = |x|r < +^, r G N^>, k(n) 6 to,   1 6 p 6 to (p = ro, |x|r = sup kxnk/^ar(n), r G N^ , a 6 ar(n) 6 ar+1 (n), r,n G N, с топологией, задаваемой системой преднорм (| • |r)Г=1.

Пространства Фреше, которые изоморфны пространствам К¨ете с определяющими матрицами Кете l _p [a _r (n)], имеющими следующее свойство: aa + ⁽^ П ) ^Р 0 при n Tro для любого r ∈ N, называют (правильными) пространствами К¨ете с правильным базисом ортов .

Матрицу [ar (n)] в этом случае называют правильной. Если пространство Фреше E изоморфно блочному пространству Кете lp ([ar(n)], lp(n)^ с правильной матрицей [ar(n)] и хотя бы для одного индекса n размерность k(n) бесконечна, то в этом случае будем говорить, что базис ортов этого пространства К¨ете упорядочиваемый, а E имеет упоря- дочиваемый p-абсолютный базис.

Легко показать проверкой (5), что если пространство Фреше E имеет представление

(1M ( n ) l p

) ) , где все размерности M (n)

в виде блочного пространства Кете вида lp I [ar (n)], блоков бесконечны, то любая p-абсолютная базисная последовательность, порождающая дополняемое подпространство в E , квазиэквивалентна части канонического базиса. Любые два p-абсолютных базиса такого пространства квазиэквивалентны [6].

Вопрос о квазиэквивалентности p-абсолютных базисов в случае пространств К¨ете — Фреше, имеющих p-абсолютный упорядочиваемый базис, до конца пока не исследован.

Свойство «густоты» базисов или самих пространств Фреше, имеющих представление в виде блочных пространств К¨ете со всеми бесконечными размерностями блоков или, в некоторых случаях, изоморфных своим декартовым квадратам, позволяет дать сравнительно просто положительный ответ на вопрос о квазиэквивалентности -абсолютных базисов дополняемых подпространств подходящим частям произвольного -абсолютного базиса всего пространства (см., например, [6]). Здесь, в частности, имеется в виду справедливость такого утверждения для пространств Фреше, имеющих правильный p- абсолютный базис и изоморфных своему декартову квадрату.

Аналогичные утверждения получаются и для в некотором смысле «разреженных» или лакунарных пространств степенных рядов [6]. Дадим абстрактное определение такого типа пространств без использования понятия правильного базиса.

Определение 2. Базис (e _n ), пространства Фреше Е назовем неоднородным , если из него нельзя выделить две подпоследовательности без общих элементов, которые были бы квазиэквивалентными.

Примерами неоднородных базисов могут служить базисы в ультраядерных пространствах К¨ете, рассматривавшихся ранее М. М. Драгилевым. Эти пространства называют теперь нестабильными .

Легко привести примеры декартовых произведений пространств лакунарных степенных рядов с неоднородными базисами, не являющимися правильными (см., например, [6]). Рассмотрим блочное расширение класса пространств К¨ете с неоднородными базисами ортов.

Определение 3. Будем говорить, что пространство Фреше — К¨ете E имеет блочно- неоднородное представление, если оно изоморфно блочному пространству К¨ете вида

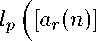
(lM ⁽ⁿ⁾))

, где (n) 6 го, n Е N, а матрица Кете [ar(n)] определяет неодно родный базис ортов в пространстве lp[ar(n)]. В последнем случае также будем говорить о неоднородности матрицы [ar(n)].

Условие неоднородности матрицы К¨ете имеет вид:

3 r(1) V r(2) 3 r(3) V r(4)

sup

{

^a r(3) ^{( n} k ^{) a} r(1) ^{( m} k )

a r(4) (m k )a r(2) (n k )

^a r(3) ^{( m} k ^{) a} r(1) ^{( n} k )

a r (4) Cn k )a r (2) (m k )

k Е n| =

∞ ,

для любых непересекающихся последовательностей (n k ), (m k ) натуральных чисел без повторений. Класс пространств Фреше — К¨ете, имеющих блочно-неоднородное представление, включает в себя в качестве собственных подмножеств классы ультраядерных

(нестабильных) пространств, различные обобщения пространств лакунарных степенных рядов, их декартовы произведения и «ручные» пространства степенных рядов бесконечного типа (подробнее см. [6]).

Теорема 1 (см., например, [6]) . Пусть пространство Фреше — К¨ете E имеет блочно неоднородное представление с p-абсолютным базисом ортов (e n ) , F — дополняемое подпространство в E и (f m ) — p-абсолютный базис в F. Тогда (f m ) квазиэквивалентен некоторой подпоследовательности базиса (e n ). Любые два p-абсолютных базиса такого пространства квазиэквивалентны.

Пусть в пространстве Кете E = l p [a r (n)] (p >  1) дополняемое подпространство F имеет p-абсолютный базис (f n ), т. е. изоморфно пространству Кете l _p [ | f n | r ]. Выбрав некоторый проектор Q из E на F будем считать, что система (полу)норм ( | • | r ) в E определена таким образом, чтобы выполнялись неравенства (3) и (4).

Выберем произвольно конечный набор элементов { f m ₁ , f m ₂ , . . . , f m _k } из базиса в F и обозначим F ^ = span(f m i ) k ₌₁ — линейную оболочку указанного набора элементов (ц = { m i , m 2 ,...,m k } ). Выделим теперь все элементы базиса ортов (e n ), для которых можно подобрать хотя бы один индекс m i с оценками норм соответствующих элементов

| e n | r | f m _i | s

| f m | r +6 | e n | s +6 6 ^{, ,} ^

Множество всех указанных ортов записываем в виде { e _n 1 , e _n 2 ,..., e _{n j} } , v(ц) = { n i } j =i , а порождаемое ими подпространство обозначим E _v(^) . Нас интересует здесь исключительно возможность случая конечных k > j . Этот случай заведомо не может иметь места, если сужение проектора

Pve = 'У еП(е)еп, e € E, n∈ν на Fµ инъективно. Поэтому основным вопросом является следующий: будет ли отображение Pv(^) : F^ ^ Ev(^) инъективно, т. е. будут ли различные векторы из F^ иметь различные проекции в Ev(^) ?

Покажем, что если дополнительно допустить, что все проекторы вида P ν и Q µ (v, ц С N) коммутируют, то случай k > j приводится к противоречию.

Следующее утверждение из [6] приведем для полноты изложения с доказательством, так как в нем содержится альтернативный подход к решению вопросов характеризации базисов по отношению к предлагаемому ниже с использованием простых возмущений базисов.

Теорема 2. Пусть F — дополняемое подпространство в пространстве Кете E = l _p [a r (n)] . Если F имеет p-абсолютный базис (f m ) и коммутируют все проекторы вида

Pve = Een(e)en’ Q^ = E fm(Qefm, e G E, n∈ν m∈µ где Q — некоторый проектор из E на F, v, ц С N, (en) — базис ортов в E, то базис (fm) квазиэквивалентен части базиса (en). В частности, если (fm) другой p-абсолютный базис в E, то при том же условии он квазиэквивалентен базису ортов (en).

<1 Будем предполагать системы полунорм (| • |r) и (k • kr) в E и F выбранными таким образом, чтобы выполнялись описанные выше неравенства (3),(4) с проектором Q. Для произвольного конечного набора ц индексов базиса (fm) рассмотрим определенный выше набор индексов v(ц) и убедимся, что случай k > j, где k — число элементов в ц, а j — число элементов в v(^), не может иметь места. В случае k > j непременно найдется элемент

k eo = Ef = 52 en(eo)en = o.

i=1            n / v ( ^ )

Если размерность подпространства F^o, порождаемого такими элементами, строго боль- ше 1, то уменьшая каждый раз число элементов в наборе {fm1 , .

. , f m _k } на единицу, мы

.

можем уменьшить число линейно независимых векторов в F ^ o не более чем на единицу. Поэтому таким уменьшением числа элементов в µ можно придти к рассмотрению новых наборов ^ i С ^ и v(^ 1 ) таких, что F ^ 1 o имеет размерность 1. Соотношение между числами элементов в ^ и v(^ 1 ) теперь не имеет значения и противоречие будет в том, что найдется индекс n £ N \ v(^ 1 ), для которого имеется индекс m i £ ^ 1 :

^|e n ^{| r lf m} i ^{| s}    6 1, V r,s £ N,

| f m i | r +6 | e n | s +6

но все такие индексы должны быть в v(^1). Итак, пусть элемент eo = 52 fm(eo)fm = 52 en(eo)en mE^1               n/v (^1)

порождает F_w o - Тогда в силу предположения о коммутирующих проекторах P _v ( ^ 1 ) и Q ^ 1 справедливо представление Q ^ 1 (I — P _v ( ^ 1 ) )Q ^ 1 e = e O (e)e o , e £ E и функционал e O удовлетворяет оценкам

| e 0 (e) l| e o | r 6 | e | r +3 , r £ N, e £ E.

Применяя утверждение леммы к разложению элемента e o по базису (f _m ), можно указать элемент f _m с m £ ^ 1 такой, что

^|e o |r ^|f m|s , v, _м ---.—.---⁶ 1, V ^{r,s £} N.

| f m | r +3 | e o | s +3

С другой стороны, применение утверждения той же леммы к разложению e o по базису (e n ) дает элемент e n с n £ v (^ 1 ):

'    '        6 1, V r,s £ N.

| e n | r +3 | e o | s +3

Но тогда найденному индексу m из ^ 1 соответствует индекс n из N \ v(^ 1 ), для которого

| e _n | _r | f _m | _s .---- 6 1 , ^{V r,} s Е N,

^|f m ^| r +6 ^|e n | s +6

а это противоречит тому, что в v(^) содержатся все такие индексы. B

Замечание. В общем случае некоммутирующих проекторов P _v , Q ^ по элементу e o из доказательства предложения можно определить и непрерывный линейный функционал e o такой, что e o (e o ) = 1, но пока не удается получить требуемых неравенств (6).

Немного иначе: можно ли для элемента e o = Q ^ (I — P _v ( ^ ) )Q ^ e o из приведенных рассуждений определить функционал e ⁰ _o : e ⁰ _o (e o ) = 1 и

^|e 0 ^{(e)| 6 inf} r

Q . I р . Q . '

^|e 0 | r

, e £ E ?

Приведенные в доказательстве предложения рассуждения можно повторить в ситуации, когда p-абсолютные базисы (e n ) и (f m ) определяют почти коммутирующие семейства проекторов в следующем смысле: для любых конечных наборов индексов µ и ν существует проектор R µ _ν :

R^ve = lim [Q^(I - Pv)QM]ne, n→∞ и семейство проекторов Rµν равностепенно непрерывно, т. е. для любого r существуют C(r) > 0, s(r) G N такие, что

|R^ve|r 6 C(r)|e|s(r), e G E, где C (r) и s(r) не зависят от числа элементов во множествах ^ и v .В этом случае базисы (en) и (fm) квазиэквивалентны, однако остается открытым вопрос описания множества пар базисов с указанным свойством.

Пусть снова ^ = {mi,...,mj'+i} и vr(g)(^) = {ni,... ,nj} — множества индексов базисов (fm)m=i и (en)n=i, соответственно, определенные выше, после леммы. Наше отрицание условий теоремы Холла — Кенига состоит в том, что размерность F^ = span(fmi )j=1 выше размерности Evr№(^) = span(eni)j=p Существование элемента fo = E fm(fo)fm =   E   en(fo)en mE^                 neN\vr(0)(^)

влечет существование хотя бы одного элемента f m _i(0) такого, что

|fmi(0) |r = kfmi(0) kr 6 k(I   Pv)fmi(0) Hr, для бесконечного числа значений r ∈ N.

Выбрав один такой элемент и считая его индекс равным m j +i , определим конечномерное возмущение базиса (f _m ) “ =i следующим образом: Sf m = f m , m = m i , i = 1, 2,..., j ; Sf m i = P v _r(0) ( ^ ) f m i + ae n i , i = 1, 2,..., j, где a выбрано так, что

2 I Pvr(0) (^)fmi | r 6 I Sfmi | r 6 21 Pvr(0) M fmi | r, i = 1, 2, • • • , j, и любого r ∈ N. Кроме того, ввиду конечномерности описанного возмущения I - S , можно всегда подобрать α, чтобы не существовало нетривиальных разложений нуля по системе (Sfm)“=i. Согласно сказанному в первой части заметки, это построение приводит к базису (Sfm)“=i, полученному из (fm)“=i автоморфизмом S.

Сравнивая базисы (en)n=i и (Sfm)“=i, предварительно выбрав систему полунорм, задающую топологию E таким образом, что элементы Sfm будут выступающими, применением соображений леммы устанавливаем, что в них элементу Sfmj+1 не может соответствовать ни один из элементов набора vr(o)(^), так как соответствующий элементу Sfmj+1 координатный функционал биортогональной последовательности обращается в ноль на всем подпространстве EVr№(^) по построению. Таким образом, существует элемент enj+1, nj+i / vr(o)M такой, что lenj+1lr|fmj+1ls

^|f m j₊1 | r +i ^|e n j₊i ^| s +i

6 C s ,   r, s ∈ N,

здесь константа C _s > 0 может зависеть не только от s, но и от ^, v _r (o) (^).

Поясним, что зависимость константы C s > 0 от указанных факторов проверяется, если проследить оценки норм оператора S и его обратного S ^-1 (особенно обратного). Привести к противоречию наше отрицание условий теоремы Холла — К¨енига пока не удается, но если бы удалось показать, что возмущение S всегда можно устраивать так, что нормы S и S ^-1 не зависят от выбора множеств ^ и v r (o) (^), то необходимое противоречие было бы получено и тем самым доказана квазиэквивалентность всех p-абсолютных базисов в пространствах К¨ете.

Заметим, что аналогичные соображения можно проводить и используя конечномерные возмущения базиса (f m ) „ =1 вида I - S, где Sf m = f m - P v _r(0) ( _p ) f m + h m , m/^ \{ f m _{j +1} } , Sf m = f m , m E V r (o)O ), где h m E ( I - P v _r(0) ( ^ ) )E (например, вида h m = ^ae a ( m ) , ^^{(m) / v} r (0) M).

Однако и здесь вопрос о равностепенной непрерывности всей совокупности удаляемых из множеств µ элементов остается открытым. Как и в предыдущем случае, этот вопрос сводится к вопросу возможности выбора возмущений I - S с равномерными оценками норм S и S ^-1 .

Можно сделать предположение, что развитие этого подхода с использованием конечномерных, а затем риссовских возмущений базисов позволит установить справедливость условий следующего предложения (или доказать их отсутствие).

Предложение 2. Пусть в пространстве Кете — Фреше E = l _p [a _r (n)] дан p-абсолютный базис (f _m )m_- =₁ некоторого дополняемого подпространства F и системы полунорм ( | • | _r ) Г =1 , ( k • ||_r ) Г =1 заданы, как в условии леммы, так что все элементы базиса ортов (е _п ) П =1 и базисной последовательности (f _m ) ^ =1 выступающие. Тогда, если существуют r(0) / N , k / N такие, что выполнено условие

М 6 k(o)MI, V д С N \{1,...,k}, то базисная последовательность (fm) квазиэквивалентна части базиса ортов (en).

Это утверждение следует из результатов [6, 9], леммы и того факта, что конечный набор элементов одного базиса всегда квазиэквивалентен набору такого же количества элементов другого базиса.

Условие предложения 2 — запись условия теоремы Холла — К¨енига существования системы различных представителей совокупности множеств v _r (o) (m), m > k. Эти условия легко проверяются с применением леммы в следующей теореме.

Теорема 3. Пусть в пространстве Кёте l _p [a r (n)] , 1 6 p <  го , p-абсолютная базисная последовательность (f _m ) „ =1 порождает дополняемое подпространство и удовлетворяет следующему условию: существует натуральный индекс r(0) >  1 такой, что при любом выборе конечных наборов ^ = { m 1 ,m ₂ ,... ,m j } и v _r (o) k) = { n 1 , n ₂ ,..., n } , k < j, описанных выше, конечномерные возмущения базиса (f m ) ^ =1 вида I — S, где Sf m = P v _{r (0)} (p) f m + ah m , m = m 1 , m 2 ,..., m _k , P v _{r (0)} (_p) — естественный проектор из E на E (v r (o)M ) = span(e n i ) ^к =1 , h m E E (v^M) , Sf m = f m , m = m i , i = 1, 2,..., k,... , могут быть выбраны так, что оценки норм координатных функционалов возмущенных базисных последовательностей относительно каждой непрерывной нормы не зависят от выбора ^ и v _r (o) (^) . Тогда (f _m ) „ =1 квазиэквивалентен части базиса ортов.

В [9] показано, что если бы удалось доказать условие предложения 2, то это дало бы положительное решение трех основных проблем структурной теории пространств К¨ете: проблемы единственности p -абсолютных базисов, проблемы изоморфной классификации (существования квазидиагональных изоморфизмов изоморфных пространств) и проблемы описания дополняемых подпространств, имеющих p -абсолютные базисы.

Для положительного решения упомянутых проблем необходимо привести к противоречию при сделанных выше (в лемме и предложении 2) предположениях следующее допущение

V (M k E N) ^ ₌₁ (M k ^ro ) 3 (_№ ^ ^ k C N \{ 1,...,M k } ,

| ^ k| >  | ^v k ⁽ ^ k ) h     ^k — 1, 2, . . .

Конструкции со счетным числом простых возмущений (риссовские операторы), возможно пригодных для этой цели, будут рассмотрены в следующих публикациях.