Проведение инженерного расчета теплового воздействия элементов электронных плат

емся только рассмотрением теплового состояния печатной платы, а процессы одновременного воздействия температуры и вибрации будут рассмотрены позднее.

Итак, интересует распределение температуры по элементам печатной платы, по самой печатной плате, направление движения потоков воздуха при естественной конвективной теплоотдаче. Тепловые процессы описываются следующими уравнениями.

• 1.    Плотность теплового потока в изотропной среде с теплопроводностью λ :

• 2.    Поток теплового поля:

q = —Л grad t .             (2)

• P = — Л J_s grad T dT .         (3)

• 3.    Производительность внутренних источников тепла в зависимости от удельной объемной теплопроизводительности внутренних источников q :

• 4.    Температурное поле (уравнение Пуассона): k²T = - ¹ .                (5)

div p — q .                  (4)

a где σ – вектор теплового потока.

Для проведения инженерного анализа и определения температур радиооэлементов платы с заданной мощностью и самих плат выбрана современная CAE-система Ansys с подключаемым модулем IcePak. Данный модуль как раз ориентирован на проведение тепловых расчетов различных печатных плат с учетом естественной или вынужденной конвекции.

На первом этапе требуется загрузка цифровой модели модуля коммутации в модуль Geometry и последующее выполнение процедур по упро- щению геометрии. Из-за особенностей модуля IcePak работы со сложными геометрическими телами, операцией Simplify удаляются все отверстия в печатной плате (см. рис. 1).

Загрузка печатных дорожек печатной платы производится на этапе переноса трехмерной модели в модуль IcePak. При загрузке имеется возможность указать толщину слоев (дорожек и диэлектрика между ними), а также материал, из которого они изготовлены.

В результате импорта дорожек было получено 19 слоев (см. рис. 2) с толщинами 0.017 и 0.16 мм из материалов Cu-Pure (медь), FR-4 (диэлектрик)

и кремний см. таблица 1. Общая толщина платы с печатными слоями составляет 1.61 мм, общий вид платы приведен на рис. 3.

При постановке задачи исходили из реальных условий испытаний изделий – задана фиксированная температура на стенках термокамеры, а само изделие располагается на подставке в нижней части камеры. В модуле IcePak термокамера имеет определяется как закрытая область (Cabinet), на стенках которой устанавливается постоянная температура. Расстояние между стенками области и платой составляет от 10 (в верхней и по боковым направлениям)

Рис. 1. Общий вид упрощенной геометрии

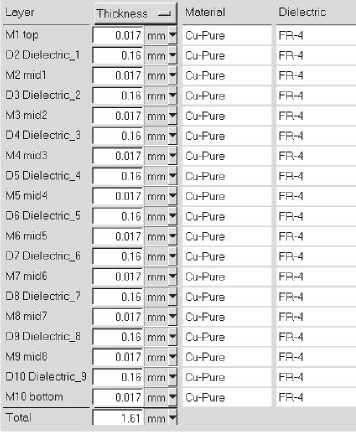
Рис. 2. Характеристики слоев печатной платы

Таблица 1. Материалы и их свойства

Материал	Плотность, м 3	Теплопроводность, M L
Медь (дорожки)	8933	387
FR-4 (диэлектрик)	1250	0,35
Кремний	2330	180

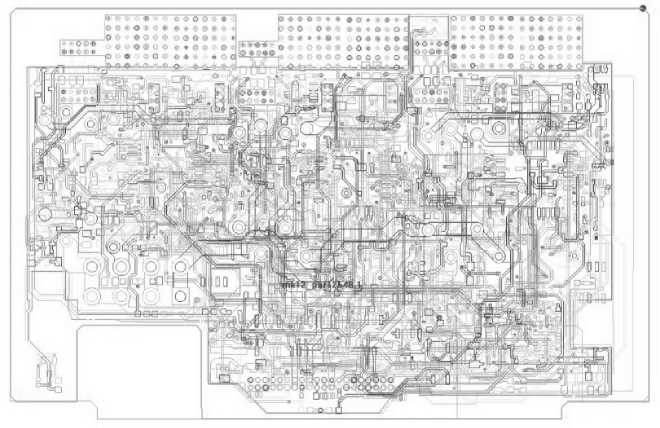
Рис. 3. Общий вид платы с печатными дорожками

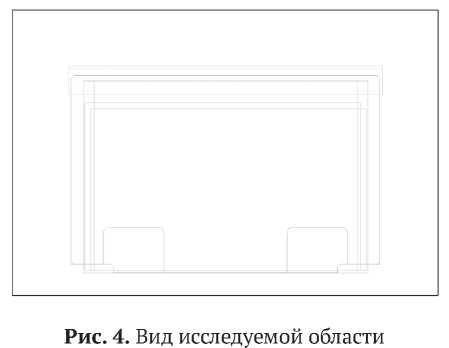
до 5 (в нижнем направлении) сантиметров. Размеры области были определены с учетом максимальных технических возможностей расчетной машины и допуска программного продукта на конечные элементы, см. рисунок 4, хотя в действительности термокамера намного больше. Были проведены дополнительные исследования по влиянию размеров термокамеры на получаемые результаты в виде распределения температуры, выявлено, что при размерах термокамеры более 5 характерных размеров исследуемого объекта результаты практически не меняются. Сразу отметим, что подобные расчеты с большим объемом термокамеры для рассматриваемой печатной платы не проводились в силу значительных затрат вычислительных ресурсов.

Далее на рис. 5 показаны фрагменты окон с заданием граничных условий на стенках закрытой области – условие непроницаемости (т.е. стенка) и фиксированная температура, которая эммулирует работу температуру внутри печи. Кроме того, для моделирования процессов естественного конвективного теплообмена задан вектор гравитации.

В результате проделанных действий была определена и параметризована исследуемая область, в которой размещено рассматриваемое

изделие с двумя печатными платами и установленными на этих печатных платах радиоэлементами. Платы при этом имеют соответствующие печатные слои с заданными толщинами и свойствами материалов. Обе печатные платы являются полностью идентичными, соответственно в дальнейшем указание мощности для радиоэлементов и изображение будут сделаны для одной из них. После подготовки окружающей области и разбиения плат на слои были заданы параметры для наиболее нагруженных радиоэлементов согласно табл. 2.

Расчет проводился при температуре стенок

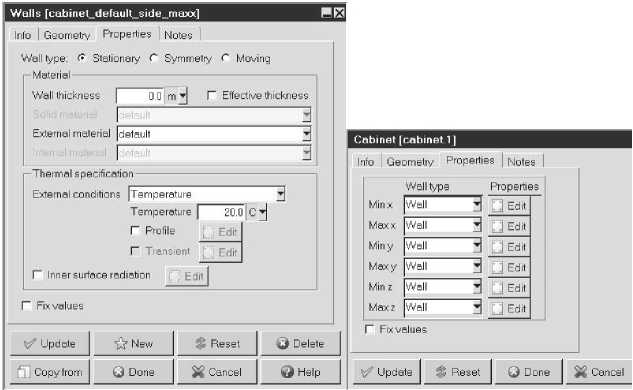
Рис. 5. Тип стенок исследуемой области и граничные условия

Таблица 2. Информация о радиокомпонентах и их мощности

Радиокомпонент	Обозначение	Рассеиваемая мощность, В
Микросхема	D4	0,148
Микросхема	D21	0,148
Микросхема	D38	0,148
Транзистор	V14	0,021
Транзистор	V15	0,021
Транзистор	V54	0,021
Транзистор	V55	0,021

Транзистор	V94	0,021
Транзистор	V95	0,021
Микросхема	Д13	0,13
Микросхема	Д14	0,13
Микросхема	D30	0,13
Микросхема	D31	0,13
Микросхема	D47	0,13
Микросхема	D48	0,13

20°С и 70°С, при этом не учитывался теплообмен посредство излучения (радиации), а также указывается ламинарный поток для движения воздуха.

В рассматриваемом модуле IcePak сетка конечных объемов генерируется путем равномерного разбиения исследуемой области в декартовой прямоугольной системе координат по трем направлениям. Отметим, что в каждом конечном объеме затем и будут производится расчеты дифференциальных уравнений, приведенных ранее. От размеров этих конечных объемов существенно зависит погрешность моделирования, так по толщине зазора рекомендуется не менее четырех конечных объемов, не говоря уже про различные пограничные слои, где желательно доводить число конечных объемов до 15-20. Однако, это уже вопрос отдельных исследований влияния количества конечных объемов на получаемые результаты и затраченные вычислительные ресурсы.

В рассматриваемой задаче минимальный размер конечного объема составляет порядка 0.001 и 0.09 мм, а максимальный – порядка 1.6 и 4.7 мм. В результате разбиения было получено 23 094 189 элементов и 23 377 514 узлов, в которых будет проводиться расчет дифференциальных уравнений.

В результате решения поставленной задачи было получено распределение температуры по печатной плате при температуре окружающей среды 20°С и 70°С, а также направление движения воздушного потока во время работы электронной платы и радиоэлементов в соответствующей окружающей области. Максимальная величина теплопроводности печатной платы составляет 387 Вт/м·К, см. рис. 6, а в целом на данном рисунке приведена эквивалентная теплопроводность печатной платы с учетом толщины проводников и диэлектриков между слоями. Максимальная температура нагретого воздуха при 20°С составляет 62°С, при 70°С – 112°С, т.е. получен приблизительно одинаковый градиент температур, равный 42°С. Максимальная температура достигается на микросхемах D4, D21, D38, см. рис. 7.

Направление движения и температура воздушного потока, создаваемого в результате нагрева радиоэлементов печатной платы, показаны на рис. 8.

Температурные поля внутри исследуемой области представлены на рис. 9.

В ходе расчетов были получены температуры исследуемых радиоэлементов для двух случаев температур окружающей среды (20°С и 70°С), результаты приведены в табл. 3.

В результате математического моделирования теплового процесса получено распределение температур по платам рассматриваемого изделия. При температуре окружающего воздуха +20 o C максимальная температура составила 62 ^oC, наиболее нагретые элементы D4, D21, D38 (с мощностью равной 0.148 Вт). При температуре окружающего воздуха +70 ^oC максимальная температура составила 112 ^oC, а наиболее нагретыми

Рис. 6. Величина теплопроводности печатной платы

Рис. 7. Распределение температуры по печатной плате при температуре окружающей среды 20°С

Рис. 8. Направление движения воздушного потока

Рис. 9. Распределение температурного поля внутри исследуемой области

Таблица 3. Температурные значения радиоэлементов

Радиокомпонент	Обозначение	Рассеиваемая мощность, Вт	Средняя температура, °С, при окружающей температуре 20°С,q	Средняя температура, °С,при окружающей температуре 70°С,q
Микросхема	D4	0,148	61	112
Микросхема	D21	0,148	62	112
Микросхема	D38	0,148	61	112
Транзистор	V14	0,021	42	106
Транзистор	V15	0,021	42	108
Транзистор	V54	0,021	43	111
Транзистор	V55	0,021	43	110

Транзистор V94 0,021 43 111 Транзистор V95 0,021 42 108 Микросхема Д13 0,13 58 93 Микросхема Д14 0,13 60 93 Микросхема D30 0,13 60 93 Микросхема D31 0,13 61 93 Микросхема D47 0,13 61 93 Микросхема D48 0,13 58 93 элементами остались те же D4, D21, D38. Температура самих печатных плат достигла значений порядка 61.7 oC и 111.8 oC в местах контакта с радиокомпонентами.

Расчет проводился при помощи CAE-системы Ansys с подключаемым модулем IcePak. Для расчета была построена сетка конечных объемов с 23 млн. элементов и 23.3 млн. узлов. Весь расчет с двумя вариантами температуры окружающей среды проведен в течение 51 часа от начала подготовки цифровой модели до получения конечного результата. Расчет проводился на вычислительной машине с 64 процессорами и 128 Гб оперативной памяти.