Проверка численной модели течения конвективной струи вблизи бокового колпака

В производственных зданиях одной из наиболее часто встречающихся вредностей, выделяющихся в результате различных производственных процессов, является тепло. При отклонении уровня нормальной для человека температуры воздуха 23–25 С (производительность при такой температуре принимается 100%, а физическое состояние оценивается как норма) производительность и самочувствие человека, находящегося в помещении, снижается.

Для наиболее эффективной работы системы вентиляции в помещениях с теплоизбытками совместно с общеобменной используется местная вытяжная вентиляция [1]-[3]. Авторами Сотниковым А.Г и Боровицким А.А. [1] проведен анализ основных типов и конструкций местных вытяжных устройств, а также предложен аналитический метод обобщения исследуемой эффективности [2]. В работе [3] исследовано изменение воздействия сварочного дыма в отсутствии и при наличии местной вытяжной вентиляции при реконструкции цеха медного комбината. .

Для определения наиболее эффективной местной системы вентиляции важно знать характеристики вредных веществ, распространяющихся в помещении в результате производственного процесса. Так, в работах, в которых исследуются характеристики свободной плоской [4]-[6] и осесимметричной [7] конвективной струи, возникающей у вертикальной пластины и у горизонтального теплоисточника. В работе [4] авторы исследовали конвекцию над горизонтальным источником, заделанным заподлицо при использовании разных вариантов моделей турбулентности. Посохин В.Н, Зиганшин А.М., Романов С.В. [5] численно исследовали естественную конвекцию у горизонтального заглубленного источника. Как изменяется эффективность теплоотдачи от вертикальной стенки, обдуваемой воздухом было рассмотрено в работе [6]. Авторы работы получили зависимости критерия Нуссельта от скорости воздуха, обдувающего нагретую пластину.

Известны работы, в которых рассматриваются эффективность улавливания пылевых частиц [8] и конвективного тепла [9] местными боковыми отсосами-раструбами. В данных статьях авторы изучали вихревые зоны у местных отсосов и их влияние на эффективность улавливания. Сравнение эффективности боковых отсосов при улавливании газовых и тепловых выбросов приведено в статье [10]. Представлена эффективность работы системы местной вытяжной вентиляции при наличии паров и дыма, а также предложены рекомендации по улучшению работы системы [11].

На эффективность работы местной вытяжной вентиляции также оказывает влияние воздушный поток, направляющий вредные выделения в сторону вытяжного отверстия [12]. В работах [12]-[14] рассматривается численное моделирование работы местных вытяжных устройств при совместной работе с приточными струями. При этом получено, что существует максимальное значение расхода приточного, увеличение которого не приводит к увеличению эффективности работы местного отсоса [13].

Для получения адекватных результатов численного решения необходимо выбрать наиболее подходящую комбинацию модели турбулентности и пристеночных функций – математическую модель. В программном комплексе Fluent существует ряд моделей турбулентности, каждая из которых имеет свои разновидности, и, кроме этого, ряд пристеночных функций.

Данным исследованиям посвящено много работ [15]-[22]. Одной из самой часто используемой модели турбулентности является модель k- ε в сочетании с пристеночной функцией Standard Wall Function (SWF) [16]. Эта модель турбулентности используется для расчётов вблизи стенок, рядом с которыми возникают вихревые зоны и отрыв струи. Автор статьи, сравнивая модели k- ε SWF, k-ω «стандартная» k-ω Standard и k-ω SST с результатами физического эксперимента, говорит, что k-ε SWF не только имеет наименьшие отклонения от результатов эксперимента, но и то, что это самый быстрый способ расчёта. Автор следующей статьи, сравнивал между собой модели турбулентности «стандартная» k-ε Standard, k-ε RNG и k-ε Realizable [18]. Модель RNG лучше модели Standard так как, она имеет дополнительный член в уравнении диссипации, который в свою очередь улучшает точность вычислений. Но также RNG не стоит выбирать для решения задачи, если скорость потока большая, так как, это приводит к существенным погрешностям. Модель турбулентности k-ε Realizable лучше использовать для круглых сечений, в противном случае результаты получаются неудовлетворительными [18]. Также, стоит учитывать, что пристеночные функции RNG и Realizable очень похожи в начале пути, но по мере удаления от истечения, линии тока рознятся [19]. Сравнивая k-ε SWF, k-ε N-EWF, k-ω SST с результатами физического эксперимента, учёные следующей статьи, пришли к выводам, что модель k-ω SST даёт сильные погрешности в начале истечения струи воздуха, все остальные значения имеют допустимые погрешности [20]. Изучая значения КМС, полученных при разных моделях турбулентности, а именно k-ε SWF, k-ε EWT, RSM SWF, RSM EWT, k-ω и далее сравнивая результаты со значениями из известного источника - справочник Идельчика и зарубежных статей, пришли к выводу, что RSM SWF и k-ε EWT это лучшие модели, так как при них получились значения более близкие к экспериментальным. Но модель RSM SWF имеет нехарактерную форму в области замыкания вихревой зоны, поэтому авторы рекомендуют использовать в расчётах модель k-ε EWT [21], [22].

Большое количество моделей турбулентности с различным числом дифференциальных уравнений приводит к отсутствию единого мнения о том, какая из комбинаций более точно описывает тот или иной процесс. Таким образом необходимо при решении конкретных задач подтверждать их достоверность.

Целью исследования, представленного в статье, является выбор модели численного решения, наиболее адекватно описывающей развитие свободной конвективной струи над плоским теплоисточником и конвективной струи около бокового отсоса, расположенного на некоторой высоте над теплоисточником. Для достижения поставленной цели задача решается в два этапа:

• -    исследование влияния комплекса моделей турбулентности и пристеночных функций на характеристики свободной конвективной струи;

• -    исследование влияния пристеночных функций на характеристики конвективной струи, развивающейся около бокового отсоса.

• 2    Materials and Methods

Задача решается численно с помощью программного комплекса Fluent.

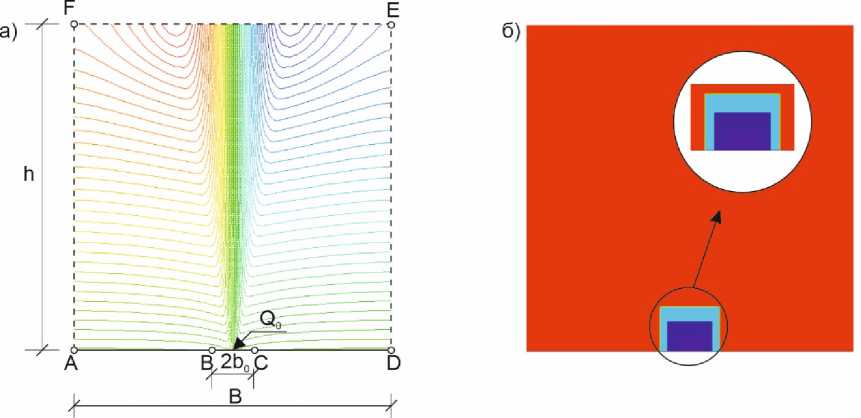
Рис.1 а) свободная конвективная струя: геометрия и линии тока; б) схема измельчения сетки области

Fig. 1a) free convective jet: geometry and streamline; b) area mesh refinement scheme

Рассматривается задача о естественной конвекции около теплоисточника, заделанного заподлицо (рис.1). Размер теплоисточника 2b 0 =0.2м, мощность Q 0 =400 Вт, размер исследуемой области: ширина - 2B=2.2 м; высота - H=2.2 м.

Для получения наиболее адекватных результатов в процессе решения необходимо добиться достаточного разрешения расчетной сетки, то есть исследовать задачу на сеточную зависимость. В качестве контролируемого параметра была принята осредненная температура на теплоисточнике - ВС.

На первом этапе было выполнено измельчение сетки на всей области исследуемой геометрии. Далее область измельчения уменьшалась. Наибольшее внимание было уделено измельчению сетки у теплоисточника. В этой области происходят ключевые процессы, наиболее заметно влияющие на конечный результат. Стратегия адаптации представлена на рисунке 1а и ниже в таблице 1.

Таблица 1. Стратегия адаптации сетки

Table 1. Mesh adaptation strategy

№ адаптации	Область адаптации
	(x 0 ;y 0 )        \	(x 1 ;y 1 )
1	Исходная сетка
2	(0;0)	(2.2;2.2)
3	(0.9;0)	(1.3;0.3)
4	(0;0)	(2.2;2.2)
5	(0;0)	(2.2;2.2)
6	(0.95;0)	(1.25;0.2)
7	(1;0)	(1.2;0.1)

В задаче рассматривается влияние использования разных моделей турбулентности, представленных в программном комплексе Fluent на характеристики струи –скорость и избыточную температуру на оси конвективной струи. Для замыкания уравнений Навье-Стокса осредненных по Рейнольдсу используются уравнения моделей турбулентности: с одним уравнением (модель Спаларта-Аллмареса), с двумя уравнениям («стандартная» k-ε (KES), RNG k-ε, k-ε realizable и «Рейнольдсовых напряжений» RSM).

На втором этапе исследований рассматривается боковой отсос шириной 2h=0.2м с постоянной скоростью всасывания u 0 =0.7 м/с, (рис. 2), расположенный на высоте h 1 =0.75м. Геометрия исследуемой области такая же как и в задаче 1. Средняя скорость всасывания определена, исходя из условий представленных в [25]:

1/3

U av = 0.032 1 ^ I     1 + 1.58 1 ¹ - 0.2 I ,                                           (1)

I b J v < b J где Qc - конвективная составляющая тепловыделения.

Исследуется изменение характеристик течения при использовании разных пристеночных функций. Вычислительный комплекс Fluent имеет в своем распоряжении две основных модели – использование пристеночных функций («стандартные» – Standard Wall Functions (SWF) и «неравновесные» – Non-equilibrium Wall Functions (NWF) и «расширенное пристеночное моделирование» (Enhanced Wall Treatment – EWT). При использовании пристеночных функций в области вблизи твердых стенок решаются специальные полуэмпирические уравнения для связывания значений на стенке и в ядре течения, получаемые при решении уравнений движения Рейнольдса.

F                             E

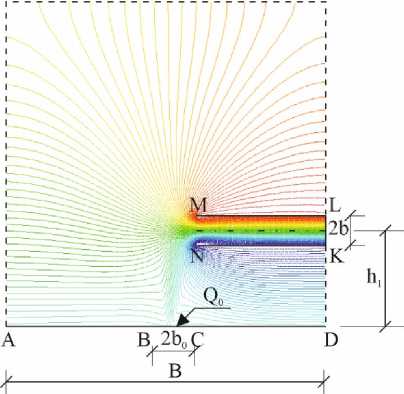
Рис. 2 Боковой отсос у теплоисточника: геометрия и линии тока Fig. 2 Side hood at the heat source: geometry and streamlines

Граничные условия, принятые в исследовании:

• -    LK (вытяжное отверстие) – Velocity inlet: равномерный профиль скорости, скорость направлена по нормали к границе: u 0 = const; k = 0; ԑ = 0;

• -    AB, CD, AF, FE, ED (свободные границы теч е ния) – Pressure Outlet: избыточное давление △ p=0; скорость направлена по нормали к границе - u = u n , dk/dn=0, dc/dn=0;

• -    BC, ML и LK (непроницаемые стенки) Wall: u = 0, (du n )/dn=0; здесь d/dn – производные по нормали к границе.

В результате решения получены изменение осевых параметров конвективной струи. Результаты представлены в безразмерном виде:

Для выбора наиболее адекватной модели численного решения, полученные результаты сравнивались с известными теоретическими данными для свободной конвективной струи [26], [27].

• 3    Results and Discussion

Линии тока течения, полученные при использовании разных вариантов моделей турбулентности, показывают схожий качественный характер течения свободной конвективной струи, возникающей у теплоисточника (рис.1а). Исключение составляет k-w модель, в случае которой происходит искривление струи, что говорит о неадекватности модели и невозможности ее использования для решения задач о естественной конвекции (рис.3).

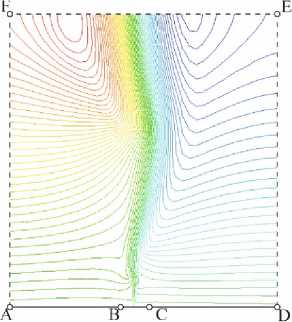
Рис. 3 Линии тока свободного конвективного течения, модель k-w Fig. 3 Streamlines of free convective flow, model k-w

При проведении верификации построены значения средней температуры на теплоисточнике, найденные на каждом этапе измельчения сетки и для каждого из исследованных сочетаний моделей. Были исследованы следующие сочетания моделей турбулентности и пристеночных функций: k- ε standard SWF/NEWF/EWT; k- ε RNG SWF/NEWF/EWT; k- ε realizable SWF/NEWF/EWT; k- ω standard/SST; RSM linear SWF/NEWF; RSM low-re.

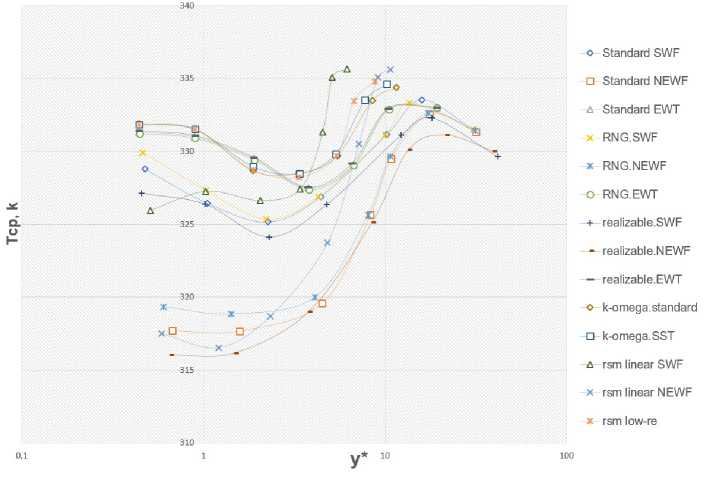
Рис.4 Изменение средней температуры на поверхности теплоисточника от y+

Fig.4 Change in the average temperature on the surface of the heat source from y+

На рисунке 4 видно, что относительно стабильный характер поведения скорости при измельчении сетки наблюдается для сочетаний: SKE NEWF, RNGKE EWT, RSM low-re, realizable NEWF и realizable EWT. Для этих моделей максимальный разброс значений на последних адаптациях сетки (при y+<5) не превышает. 0.1%. Остальные модели показывают разброс от 0.5% до 1%, что можно также считать допустимым.

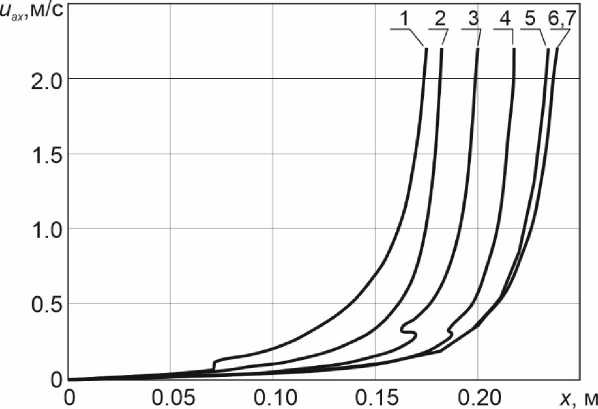
Рис. 5. Изменение осевой скорости свободной конвективной струи при разных адаптациях Fig. 5 Variation of the Axial Velocity of a Free Convective Jet with Different Adaptations

На рисунке 5 представлен график зависимости осевой скорости по высоте конвективной струи при сочетании стандартной k- ε модели турбулентности с неравновесными пристеночными функциями (NEWF) для разной степени измельчения сетки. Видно, как на первых адаптациях происходит изменение параметров относительно друг друга. Так, к примеру максимальное различие значений осевой скорости между первой и второй адаптацией 16.7%, когда между 5 и 7 адаптацией максимальное отклонение не превышает 1.67%, а значение при 6 и 7 адаптациях совпадают, что говорит о достаточном разрешении сетки и возможности дальнейшего ее использования.

Результаты, полученные численно сравнивались с результатами, вычисленными по формуле для определения осевой скорости (2), представленной в [24] и формуле (3) [25]:

u y

u y

( g^Q PP, ^Td )

1 + Pr —1/3 = 3----- ^Ly

4Pr t

erf I

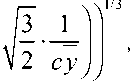
uy             0,065 Qc ^1/3

uy = rp~ --— = ^—--ТГ , Ц ( g^Qc/^c P T , ) у ( g^Q. cp P , T , )

где: u y - безразмерная осевая скорость; с p – теплоемкость воздуха, ρ ∞ - плотность воздуха на бескон е чности при температуре окружающего воздуха Т ∞ , Pr t – турбулентное число Прандтля (0.85), у = у / ь 0 - безразмерная координата.

Численное решение показало, что при использовании разных моделей турбулентности получаются разные значения конвективной и радиационной составляющей тепловыделений (таблица 1). Конвективная составляющая Q_c далее использовалась в расчетах (формулы 2 и 3).

Таблица. Радиационная и конвективная составляющие

Модель турбулентности	k-ɛ стандартная	k-ɛ realizable	k-ɛ RNG	RSM	SA
Q rad	51.82	45.27	53.35	43.7	54. 13
Q конв	28.18	34.73	26.65	36.3	25. 87

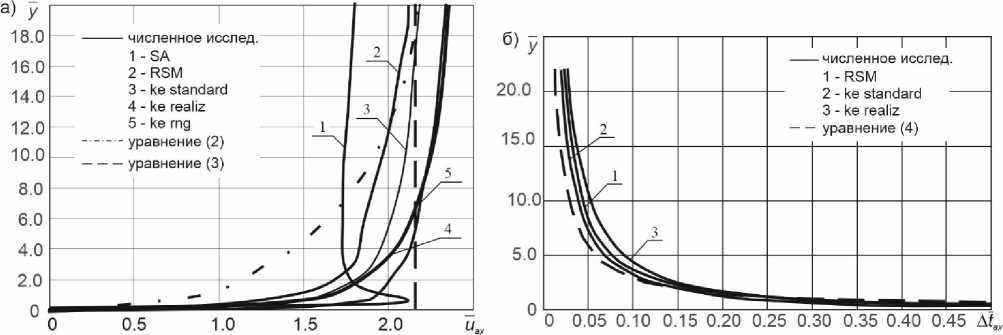
Рис.6 а) изменение осевой скорости по высоте струи при использовании разных моделей турбулентности; б) изменение избыточной температуры по высоте струи при использовании разных моделей турбулентности

Fig.6 а) change in axial velocity along the height of the jet when using different turbulence models; b) change in excess temperature along the height of the jet when using different turbulence models

На рисунке 6а представлено изменение осевой скорости в струе при использовании различных моделей турбулентности. Там же показаны линии, полученные по формулам (2) и (3).

На расстоянии примерно 12b 0 струя имеет начальный участок. В этом случае формула (3) не имеет смысла, так как пригодна только для основного участка струи. На основном участке наиболее адекватные результаты получаются при использовании моделей k- ε стандартная и RSM.

На рисунке 6б представлены изменения безразмерной избыточной температуры по длине струи, полученные численно и по формуле (4) [25].

∆ t y

0, 064 Q c ^2/3 y ^{- 1}

,

∞

где: ∆ t y - безразмерная избыточная температура на оси струи.

Результаты, полученные численно близки друг другу. Наиболее близкое значение к теоретическим данным дает использование стандартной k- ε модели.

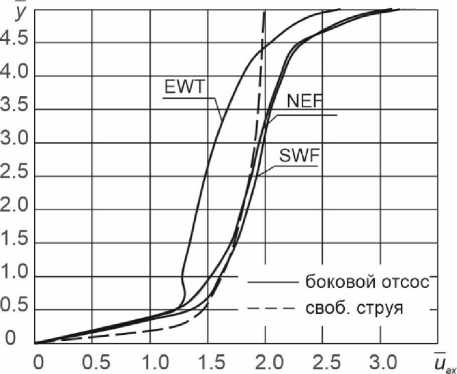
Рис.7 Изменение осевой скорости по высоте струи при использовании разных пристеночных функций

Fig.7 Variation of the axial velocity along the jet height when using different near-wall functions

Как и ранее определена осевая скорость конвективной струи (максимальная скорость в сечениях), развивающейся около бокового отсоса. Рисунок 7 показывает, как влияет использование разных пристеночных функций на изменение скорости струи. Для сравнения полученных результатов на рисунке приведена линия, показывающая изменения осевой скорости в свободной конвективной струе. Наиболее близкие результаты дают использование стандартных пристеночных функций и неравновесных.

• 4    Conclusions

В результате численного исследования рассмотрены все варианты комбинаций модели турбулентности с пристеночными функциями для свободной конвективной струи. Результаты показали, что наиболее близкие результаты к теоретическим исследованиям дает использование стандартной k- ε модели совместно со стандартными пристеночными функциями.

Данная модель численного решения будет использована в дальнейшем при исследовании разных вариантов использования бокового отсоса около теплоисточника.