Проверка гипотезы нормальности числа падения овсяной муки по малым выборкам

При проведении прямых измерений требуется статистическая обработка их результатов с установлением принадлежности получаемого эмпирического распределения теоретическому распределению. Условием проверки гипотезы нормальности по совокупности малых независимых выборок является наличие их достаточно большого числа при одном и том же объеме. В таком случае можно проверить «…гипотезу нормальности генеральных совокупностей, из которых были взяты изучаемые выборки при допущении, что параметры этих совокупностей имеют разные значения» [1]. К изучению принимается относительное отклонение, равное xik   xk

S k

где x ik – i -й элемент k -й выборки; x , S . – среднее и среднеквадратичное отклонение k -й выборки.

Следует учитывать, что распределение величины τ не зависит от параметров генеральной совокупности: количества выборок и величины стандартного отклонения, а зависит только от объема выборки. Плотность вероятности величины τ выражается следующим образом:

f ^(т )

П 4 f + 1

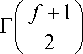
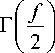
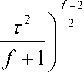
при | Т <  4 f + 1;

0 при IT>4f + 1, где f – число степеней свободы, определяемое как уменьшенный на два объем выборки (число измеряемых определений). При прогнозировании расхождения эмпирического распределения с теоретическим полагают, что уже «…при четырех повторностях измерений в малой выборке относительные отклонения в отдельных выборках в изучаемой совокупности могут подчиняться равномерному распределению, если исходные совокупности нормальны» [1]. Если число выборок достаточно велико, то данное условие позволит выполнить проверку гипотезы нормальности. Обычно при проверке гипотезы нормальности по большому числу малых выборок из каждой выборки случайным образом отбирается по одному значению только первых, вторых и т. д. измерений, допуская, тем самым, упрощение и случайный отбор данных. Например, при объеме выборки в четыре измерения плотность вероятности величины τ приобретает вид:

f^{(т ) =} 213 при ^Т * <  ^3.       ⁽³⁾

В рекомендациях [2] изложены правила проверки опытного распределения с теоретическим при проверке простых и сложных гипотез путем применения критериев согласия Колмогорова, Смирнова и ω2 Мизерса. Вначале определяются со сложностью проверяемой гипотезы, а в самом процессе проверки согласия по выборке вычисляют значение статистики используемого критерия. Считается, что «…распределения статистик непараметрических критериев как при простых, так и сложных гипотезах очень быстро сходятся к предельным законам», не допуская ошибок при анализе данных с числом малых выборок более 15÷20. Малый объем выборок также позволяет «…успешно различать близкие гипотезы», что представляется удобным при разработке выборочного плана.

Объектом данного исследования являются малые выборки числа падения овсяной муки, используемой в хлебопекарном производстве при выработке хлебопекарной продукции повышенной пищевой ценности [3], в том числе при составлении композитных смесей с различными видами муки [4, 5]. Как показывают исследования, «…овсяная мука, как и другие виды муки из крупных культур, отличается от традиционной хлебопекарной муки специфическими технологическими свойствами, в том числе отсутствием способности образовывать клейковину. Автолитическая активность подобного сырья в силу специальной технологии получения крупы и удаления анатомических частей определяется не столь активностью амилолитических ферментов, расщепляющих крахмал до низкомолекулярных декстринов и олигосахаридов, сколько степенью автолиза крахмала и накоплением водорастворимых веществ при прогреве водномучных суспензий. Качество крупяной продукции может определяться на основе инструментальной оценки проб муки стандартным методом числа падения, реализуемым в условиях внутризаводского контроля. В качестве улучшителей амилолитической активности муки из крупяных культур следует рассматривать зерновые продукты и их композиции, определяющие получение феноменологической модели прогнозирования варочных свойств готового продукта» [6].

Целью данной работы явилась проверка гипотезы нормальности числа падения овсяной муки по малым выборкам эксперимента с использованием непараметрического критерия согласия ω2 Мизерса, поскольку, в отличие от широко применяемого критерия χ2 Пирсона, рассматриваемый критерий «…основывается на непосредственно полученных в эксперименте несгруппированных значениях случайной величины» [1].

Shmal’ko N.A. et al. Proceedings of VSUET, 2023, vol. 85, no. 1, pp. 118-126 Материалы и методы

Материалом исследования являлся образец овсяной муки, соответствующий требованиям

СТО 53548590–019–2013 (ООО «ХЛЕБЗЕРНО-ПРОДУКТ», г. Таганрог, Ростовская область). Число падения овсяной муки определяли по стандартному методу ГОСТ 27676–88 [7]: «…сущность которого заключается в определении времени свободного падения шток-мешалки в клейстеризованной водно-мучной суспензии». За окончательный результат числа падения принимают среднее арифметическое результатов параллельного определения двух навесок, допускаемое расхождение между которыми не должно превышать 10% от их средней арифметической величины. При превышении допускаемого расхождения определение повторяют. Вычисления проводят до первого десятичного знака с последующим округлением результата до целого числа.

В данном стандарте приводятся правила округления повторных результатов измерений, производимых двухканальной измерительной системой прибора типа ПЧП. Так, в примере 1 результат определения по первой навеске составляет 150 с, по второй – 160 с. Среднее арифметическое значение – 155 с. Допускаемое расхождение от этого среднего арифметического значения составляет 15,5 с. Фактическое расхождение между результатами параллельного определения двух навесок составляет 10 с, что не превышает допускаемого расхождения между ними. Среднее арифметическое значение (155 с) принимают за окончательный результат определения числа падения.

При контрольном (повторном) определении числа падения допускаемое расхождение между контрольным (повторным) и первоначальным определением не должно превышать 10% от их средней арифметической величины. При контрольном (повторном) определении за окончательный результат принимают результат первоначального определения, если расхождение между результатами контрольного (повторного) и первоначального определений не превышает допускаемого значения; если расхождение превышает допускаемое значение, за окончательный результат принимают результат контрольного (повторного) определения.

В примере 2 результат первоначального определения составляет 150 с, контрольного (повторного) – 170 с. Среднее арифметическое значение – 160 с. Допускаемое расхождение от этого среднего значения составляет 16 с. Фактическое расхождение составляет 16 с.

Фактическое расхождение между результатами первоначального и контрольного (повторного) определений составляет 20 с, что превышает допускаемое расхождение. За окончательный результат определения числа падения принимают результат контрольного (повторного) определения – 170 с.

В примере 3 результат первоначального определения составляет 150 с, контрольного (повторного) – 160 с. Среднее арифметическое значение – 155 с. Допускаемое расхождение составляет 15,5 с. Фактическое расхождение между результатами первоначального и контрольного (повторного) определений составляет 10 с, что не превышает допускаемого расхождения. За окончательный результат принимают результат первоначального определения – 150 с.

Округление результатов определения проводят следующим образом: если первая из отбрасываемых цифр равна или больше 5, то последнюю сохраняемую цифру увеличивают на единицу; если меньше 5, то ее оставляют без изменения [7].

Очевидно, что при таком подходе проведение многократных (повторных) измерений для серии опытов и соблюдение правил округления приводит к получению ожидаемых одинаковых (и / или) повторных результатов от одного определения к другому, случайный характер которых либо исключается, либо носит характер равномерного распределения. В связи с этим, для изучения числа падения как случайной величины была получена совокупность малых выборок для проверки гипотезы о том, что функция распределения такой случайной величины есть F(x), для чего необходимо было построить эмпирическую функцию распределения Fn(x) для сравнения с нею путем применения непараметрического критерия согласия ω2 Мизерса от

Ю 2 = J[ Fn (x)- F (x )]25F (x) (4) -от предполагая наличие у F(x) производной, т. е. плотности вероятности, имеем выражение

dF (x ) = F'(x )dx = f (x )5x (5)

Алгоритм применения непараметрического критерия согласия ω² Мизерса при проверке гипотезы нормальности по совокупности малых выборок заключался в следующем. Вначале выборки преобразовывали в вариационный ряд x 1 <  x 2 <  x 3 <… <  x n и разбивали всю область интегрирования на интервалы (–∞, x 1 ), ( x 1 , x 2 )…, ( x n-1 , x n ), ( x n , +∞).

Принимая во внимание выражение получали

(4),

x ₁

to2

x 1                                    n -1 x k +1 Г i

"H ⁰" ^F ( x ) ]S ^F + Zj -

-^                                   k -1 -.-.   _ n

- O

+ O

+ J [ 1- F ( x ) ] ² 5 F .

xn

k - ¹ x k

k

- F ( x )   d F +

x ₁

j F ² ( x ) d F =

-O

^{F 3} ( x )

x ₁

_ F ³ ( x , )

- O

;

x k +1 ■

1k+1    k f - - F (x)  dF -

J n

^{F (} x ) ^- n

^{x -} x k + 1

xk

F ( x - + 1 ) - - _

+ O

Ш" ^F ( x ) ] 2 5 ^F =

^{F (} x - ) ^- 1.

xn

После преобразования выражение имело вид

to ² - F 3 ( x l) +£

3      t^1

F ( x - + 1 ) - ^k n

n -1

- ZL

k - 1

^{F (} x k ) - n ]

+

Объединив члены, с данными k = 1, 2…, n , суммах (8), получили

зависящие от F ( x k ) находящиеся в двух

в области больших значений ω2, существенных для вероятностной оценки.

Результаты

Выборки опытных данных числа падения овсяной муки сведены в таблицу 2. На первом этапе исследования выбирали из результатов четырех параллельных определений первое значение показателя числа падения x 1 и вычисляли для каждого из 12 выборок величину относительного отклонения τ по формуле (1), результаты расчетов приведены в таблице 3. Далее следовала проверка гипотезы нормальности распределения выборок при помощи непараметрического критерия согласия ω² Мизерса, для чего расположили полученные значения τ в вариационный ряд, и для каждого элемента ряда определяли значения эмпирической функции распределения Fn ( τ ) по формуле

Fn ( t ) - 2^k-T          (10)

где n = 12, k = 1, 2…, n и значения теоретической функции F ( τ ) по формуле (3).

Результаты расчета теоретической и эмпирической функций распределения для первого определения выборки сведены в таблице 4, где значения τ расположены в порядке возрастания.

Таблица 2.

Выборки опытных данных числа падения овсяной муки

Table 2.

to ² - ---- +

12 n ²

n

1 Z F ( x - ) - n k - 1 [

2 k -1 1 ²

2 n

Равенство (9) показывает, каким образом критерий ω² Мизерса зависит от отдельных членов вариационного ряда. Критические значения для величины n ω², т. е. квантили ( n ω²) 1-р приведены в таблице 1.

Таблица 1.

Sampling of experimental data of the falling number of oatmeal

№.	x 1	x 2	x 3	x 4
1	336	342	345	336
2	342	340	334	340
3	336	341	341	342
4	332	343	332	351
5	342	346	339	348
6	347	348	342	349
7	332	333	336	334
8	335	341	336	334
9	347	353	339	335
10	337	340	333	333
11	338	335	330	331
12	342	334	332	339

Таблица 3.

Расчет относительного отклонения для первого определения выборки

Table 3.

Calculation of the relative deviation for the first

Квантили распределения n ω ² [1]

Table 1.

Quantiles of the distribution n ω ² [1]

p	(nω2) 1-р	p	(nω2) 1-р
0,5	0,1184	0,05	0,4614
0,4	0,1467	0,03	0,5489
0,3	0,1843	0,02	0,6198
0,2	0,2412	0,01	0,7435
0,1	0,3473	0,001	1,1679

Если вычисленное значение n ω² меньше табличного ( n ω²) 1-р , то гипотеза о совпадении теоретического закона распределения F ( x ) c эмпирическим (выборочным) Fn ( x ) не отвергается, но при n ω² больше табличного ( n ω²) 1-р гипотеза отклоняется. Отмечается, что распределение n ω² значительно быстрее, чем χ² сходится к предельному закону, особенно

sample definition

№	x	S k	x 1 – x	τ 1
1	339,75	3,897	– 3,75	– 0,962
2	339,00	3,000	+ 3,00	+ 1,000
3	340,00	2,345	– 4,00	– 1,706
4	339,50	8,016	– 7,50	– 0,936
5	343,75	3,491	– 1,75	– 0,501
6	346,50	2,693	+ 0,50	+ 0,186
7	333,75	1,479	– 1,75	– 1,183
8	336,50	2,693	– 1,50	– 0,557
9	343,50	6,982	+ 3,50	+ 0,501
10	335,75	2,947	+ 1,25	+ 0,424
11	333,50	3,202	+ 4,50	+ 1,405
12	336,75	3,961	+ 5,25	+ 1,325

Таблица 4.

Расчет теоретической и эмпирической функций распределения для первого определения выборки

Table 4.

Вычисления производили, принимая во внимание, что f ( τ ) = 0 при τ < –  3 , отсюда имеем

F (т )= i ^5r=

–3²³                  (11)

T k + 73 ) , k = 1,2..., n

Отсюда, при τ 1 = -1,706

F (-1,706) =-1,7062 ^3 = —1,706 +1,732 = 0,0087.

2V3(

^{V       7}      2^3          2 - 1,732

Значение эмпирической функции определяли по формуле (10), при τ = τ 1 получили

Fn ( t ) = 2^-1 ^{v 17}    2 x 12

Расчет статистики упрощенной формуле

= 0,0417.

n ω² производили по

Для уровня значимости р = 0,05 табличное значение ( n ω²) 1-р = 0,4614, а вычисленное значение n ω² (0,03051) меньше табличного.

Следовательно, гипотеза нормального распределения малых выборок по первому определению числа падения овсяной муки не отклоняется. Для проверки данного утверждения в отношении второго, третьего и четвертого определений произвели дополнительные этапы расчетов, результаты которых приведены в таблицах 5–10.

Таблица 5. Расчет относительного отклонения для второго определения выборки

Table 5.

Calculation of the relative deviation for the second

n

nml = 12n + gLF(Tk )

—

2 k — 1 1 2

2 n

Подставив значение n = 12 и полученную из таблицы 4 сумму L F ( t ) Fn ( t ) ] получили значение статистики n ω²

n ® ² =---- + 0,023565 =

12 x 2

= 0,03051 ( для первого определения ) .

sample definition

№ выборки | Sample No.	x	S k	x 3 – x	τ 3
1	339,75	3,897	+ 2,25	+ 0,577
2	339,00	3,000	+ 1,00	+ 0,333
3	340,00	2,345	+ 1,00	+ 0,426
4	339,50	8,016	+ 3,50	+ 0,437
5	343,75	3,491	+ 2,25	+ 0,645
6	346,50	2,693	+ 1,50	+ 0,557
7	333,75	1,479	‒ 0,75	‒ 0,507
8	336,50	2,693	+ 4,50	+ 1,671
9	343,50	6,982	+ 9,50	+ 1,361
10	335,75	2,947	+ 4,25	+ 1,442
11	333,50	3,202	‒ 0,50	‒ 0,156
12	336,75	3,961	‒ 2,75	‒ 0,694

Таблица 6.

Calculation of theoretical and empirical distribution functions for the first determination of the sample

№	τ 1	F ( τ 1 )	Fn ( τ 1 )	F ( τ 1 ) – Fn ( τ 1 )	2 F ( T 1 ) - Fn ( T 1 )
1	– 0,962	+ 0,0087	+ 0,0417	– 0,0330	0,001089
2	+ 1,000	+ 0,1830	+ 0,1250	+ 0,0580	0,003364
3	– 1,706	+ 0,2567	+ 0,2083	+ 0,0484	0,002343
4	– 0,936	+ 0,2654	+ 0,2917	– 0,0263	0,000692
5	– 0,501	+ 0,3917	+ 0,3750	+ 0,0167	0,000279
6	+ 0,186	+ 0,3554	+ 0,4583	– 0,1029	0,010588
7	– 1,183	+ 0,5537	+ 0,5417	+ 0,0120	0,000144
8	– 0,557	+ 0,6224	+ 0,6250	– 0,0026	0,000007
9	+ 0,501	+ 0,6446	+ 0,7083	– 0,0637	0,004058
10	+ 0,424	+ 0,7887	+ 0,7917	– 0,0030	0,000009
11	+ 1,405	+ 0,8825	+ 0,8750	+ 0,0075	0,000056
12	+ 1,325	+ 0,8750	+ 0,9056	– 0,0306	0,000936
Σ					0,023565

Расчет теоретической и эмпирической функций распределения для второго определения выборки

Table 6.

Calculation of theoretical and empirical distribution functions for the second determination of the sample

№ выборки | Sample No.	τ 3	F ( τ 3 )	Fn ( τ 3 )	F ( τ 3 ) – Fn ( τ 3 )	F ( t 3 ) -Fn ( t 3 )
1	‒ 0,694	+ 0,2997	+ 0,0417	+ 0,2580	0,066564
2	‒ 0,507	+ 0,3536	+ 0,1250	+ 0,2286	0,052258
3	‒ 0,156	+ 0,4550	+ 0,2083	+ 0,2467	0,060861
4	+ 0,333	+ 0,5961	+ 0,2917	+ 0,3044	0,092659
5	+ 0,426	+ 0,6230	+ 0,3750	+ 0,2480	0,061504
6	+ 0,437	+ 0,6262	+ 0,4583	+ 0,1679	0,028224
7	+ 0,557	+ 0,6608	+ 0,5417	+ 0,1191	0,014161
8	+ 0,557	+ 0,6666	+ 0,6250	+ 0,0416	0,001731
9	+ 0,645	+ 0,6862	+ 0,7083	‒ 0,0221	0,000488
10	+ 1,361	+ 0,8929	+ 0,7917	+ 0,1012	0,010241
11	+ 1,442	+ 0,9163	+ 0,8750	+ 0,0413	0,001706
12	+ 1,671	+ 0,9824	+ 0,9056	+ 0,0768	0,005898
Σ					0,396295

_       1по2 = —- + 0,396295

= 0,4032 (для второго определения).

Для уровня значимости р = 0,05 табличное значение ( n ω²) 1-р = 0,4614, а вычисленное

Расчет относительного отклонения значение nω2 (0,4032), так же, как и для первого определения, меньше табличного. Отсюда, гипотеза нормального распределения малых выборок по второму определению числа падения овсяной муки не отклоняется.

Таблица 7 для третьего определения выборки

Table 7

Calculation of the relative deviation for the third sample definition

№ выборки | Sample No.	X	S k	X 3 - X	τ 3
1	339,75	3,897	+ 5,25	+ 1,347
2	339,00	3,000	‒ 5,00	‒ 1,667
3	340,00	2,345	+ 1,00	+ 0,426
4	339,50	8,016	‒ 7,50	‒ 0,936
5	343,75	3,491	‒ 4,75	‒ 1,361
6	346,50	2,693	‒ 4,50	‒ 1,671
7	333,75	1,479	+ 2,25	+ 1,521
8	336,50	2,693	‒ 0,50	‒ 0,186
9	343,50	6,982	‒ 4,50	‒ 0,645
10	335,75	2,947	‒ 2,75	‒ 0,933
11	333,50	3,202	‒ 3,50	‒ 1,093
12	336,75	3,961	‒ 4,75	‒ 1,199

Таблица 8.

Расчет теоретической и эмпирической функций распределения для третьего определения выборки

Table 8.

Calculation of theoretical and empirical distribution functions for the third determination of the sample

№ выборки | Sample No.	τ 3	F ( τ 3 )	Fn ( τ 3 )	F ( τ 3 ) ‒ Fn ( τ 3 )	№) - Fn^)]2
1	‒ 1,671	+ 0,0176	+ 0,0417	‒ 0,0241	0,000581
2	‒ 1,677	+ 0,0188	+ 0,1250	‒ 0,1062	0,011278
3	‒ 1,361	+ 0,1071	+ 0,2083	‒ 0,1012	0,010241
4	‒ 1,199	+ 0,1539	+ 0,2917	‒ 0,1378	0,018989
5	‒ 1,093	+ 0,1845	+ 0,3750	‒ 0,1905	0,036290
6	‒ 0,936	+ 0,2298	+ 0,4583	‒ 0,2285	0,052212
7	‒ 0,933	+ 0,2307	+ 0,5417	‒ 0,3110	0,096721
8	‒ 0,645	+ 0,3138	+ 0,6250	‒ 0,3112	0,096845
9	‒ 0,186	+ 0,4463	+ 0,7083	‒ 0,2620	0,068644
10	+ 0,426	+ 0,6230	+ 0,7917	‒ 0,1687	0,028460
11	+ 1,347	+ 0,8889	+ 0,8750	+ 0,0139	0,000193
12	+ 1,521	+ 0,9391	+ 0,9056	+ 0,0335	0,001122
Σ					0,421576

Таблица 9.

Расчет относительного отклонения для четвертого определения выборки

1 по2 =^—j^ +0,421576 = 0,4285 (для третьего определения).

Для уровня значимости р = 0,05 табличное значение ( n ω²) 1-р = 0,4614, а вычисленное значение n ω² (0,4285), так же, как и для первого и второго определений, меньше табличного. Отсюда, гипотеза нормального распределения малых выборок по третьему определению числа падения овсяной муки также не отклоняется.

Table 9.

Calculation of the relative deviation for the fourth sample definition

№ выборки | Sample No.	x	S k	x 4 – x	τ 4
1	339,75	3,897	– 3,75	– 0,962
2	339,00	3,000	+ 1,00	+ 0,333
3	340,00	2,345	+ 2,00	+ 0,853
4	339,50	8,016	+ 11,50	+ 1,435
5	343,75	3,491	+ 4,25	+ 1,217
6	346,50	2,693	+ 2,50	+ 0,928
7	333,75	1,479	+ 0,25	+ 0,169
8	336,50	2,693	– 2,50	– 0,928
9	343,50	6,982	+ 8,50	+ 1,217
10	335,75	2,947	– 2,75	– 0,933
11	333,50	3,202	– 2,50	– 0,781
12	336,75	3,961	+ 2,25	+ 0,568

Таблица 10.

Расчет теоретической и эмпирической функций распределения для четвертого определения выборки

Table 10.

Calculation of theoretical and empirical distribution functions for the fourth determination of the sample

№ выборки | Sample No.	τ 3	F ( τ 3 )	Fn ( τ 3 )	F ( τ 3 ) – Fn ( τ 3 )	F ( т 3 ) -Fn ( т 3 )
1	– 0,962	+ 0,2223	+ 0,0417	+ 0,1806	0,032616
2	– 0,933	+ 0,2307	+ 0,1250	+ 0,1057	0,011173
3	– 0,928	+ 0,2321	+ 0,2083	+ 0,0238	0,000566
4	– 0,781	+ 0,2745	+ 0,2917	– 0,0172	0,000296
5	+ 0,169	+ 0,5488	+ 0,3750	+ 0,1738	0,030206
6	+ 0,333	+ 0,5961	+ 0,4583	+ 0,1378	0,018989
7	+ 0,568	+ 0,6640	+ 0,5417	+ 0,1223	0,014957
8	+ 0,853	+ 0,7462	+ 0,6250	+ 0,1213	0,014714
9	+ 0,928	+ 0,7679	+ 0,7083	+ 0,0596	0,003552
10	+ 1,217	+ 0,8513	+ 0,7917	+ 0,0596	0,003552
11	+ 1,217	+ 0,8513	+ 0,8750	– 0,0237	0,000562
12	+ 1,435	+ 0,9143	+ 0,9056	+ 0,0087	0,000076
Σ					0,131259

па2 = — + 0,131259 =

12^12

0,1382 (для четвертого определения).

Для уровня значимости р = 0,05 табличное значение ( n ω²) 1-р = 0,4614, а вычисленное значение n ω² (0,1382), так же как и для всех предыдущих определений, меньше табличного. Отсюда, гипотеза нормального распределения малых выборок по четвертому определению числа падения овсяной муки также не отклоняется.

В пользу полученных результатов свидетельствует формулировка другого критерия – критерия на отклонение от нормального распределения, служащего для проверки отклонения распределения вероятностей от нормального распределения. В стандарте ГОСТ Р ИСО 5479–2002 [8] «…критерий на отклонение от нормального распределения имеет нулевую гипотезу в том случае, когда выборка из n независимых наблюдений подчиняется одному и тому же нормальному распределению». Но такой критерий для проверки гипотезы используется преимущественно при необходимости сопоставления x выборочного с x теоретическим, полученным при помощи t -критерия, т. е. параметрического критерия. В противном случае, проверке подлежит простая гипотеза с задаваемой функцией распределения, с которой наблюдают согласие с наблюдаемой выборкой.

Обсуждение

Полученные в работе результаты согласуются с общепринятыми классическими представлениями о проверке статистической гипотезы о нормальном распределении выборок. Указанные в литературе методы синтеза новых статистических критериев для проверки гипотез малых выборок с помощью аналитических и нейросетевых подходов не лишены ряда недостатков. Например, в работе [9] приводится решение задачи по поверке гипотезы нормального распределения исследуемых данных на выборках объемом от 16 до 25 опытов, адаптированных для осуществления многокритериального анализа. Однако, параллельно с ростом числа объединяемых статистических критериев (до 210) растут взаимные корреляционные связи между новыми синтезированными критериями, что ограничивает возможности указанного метода. Снижение корреляционной сцепленности искусственных нейронов добиваются объединением классических критериев не более трех с настройкой квантователей давать равные вероятности ошибок первого и второго рода [10]. В следующей работе [11] показана возможность оптимизации проверки гипотез нормальности или равномерности распределений малых выборок путем перехода от применения бинарных искусственных нейронов к троичным нейронам при совместном использовании пяти классических статистических критериев. Однако ограничением данного подхода служит использование синтетических статистических критериев при малых выборках в 16 опытов. Другой подход статистического анализа малых выборок путем синтеза новых статистических критериев включает операцию дифференцирования случайных данных малой выборки. Вероятность появления ошибок первого и второго родов снижается до 0,075, что допускается только для ряда приложений нейросетевой биометрии [12]. В данной работе вычисления произведены при р = 0,05, что обеспечивает достаточную точность изучаемого показателя (числа падения) в технических системах и не требует проведения синтеза статистического критерия для проверки гипотезы нормальности малых выборок.

Заключение

При проверке гипотезы нормальности малых выборок полагались на мнение специалистов, что уже при четырех повторностях измерений в малой выборке относительные отклонения в отдельных выборках в изучаемой совокупности могут подчиняться равномерному распределению, если исходные совокупности нормальны. Если число выборок достаточно для анализа, то данное условие позволит выполнить проверку гипотезы нормальности. Как правило, при проверке гипотезы нормальности по большому числу малых выборок из каждой выборки случайным образом отбирается по одному значению только первых, вторых и т. д. измерений, допуская, тем самым, упрощение и случайный отбор данных. Отсюда, целью исследования явилась проверка гипотезы нормальности малых выборок каждого из четырех определений числа падения, поскольку округление значений прямых измерений исключает случайный характер величины или ее нормальное распределение в пользу равномерного. В данном случае, проверке подлежала простая гипотеза с задаваемой функцией распределения, с которой наблюдают согласие с наблюдаемой выборкой при использовании непараметрического критерия согласия ω2 Мизерса. При уровне значимости р = 0,05 табличное значение (nω2)1-р больше вычисленного значения nω2 для всех четырех определений. Поэтому гипотеза нормального распределения малых выборок для всех четырех определений (как случайных величин) числа падения овсяной муки не отклоняется.

Исследования выполнялись с использованием оборудования ЦПК «Исследовательский центр пищевых и химических технологий» КубГТУ (СКР_3111), развитие которого поддерживается Министерством науки и высшего образования РФ (Соглашение № 075–15–2021–679).