Проводимость двухслойной графеновой наноленты с учетом внешнего электрического поля

Электрические свойства графитов и графитизированного углерода могут сильно изменяться в зависимости от степени кристаллического упорядочения. В случае высококачественного монокристалла графита сопротивление быстро падает с падением температуры. Такое падение происходит главным образом из-за уменьшения фононного рассеяния на низких температурах. С другой стороны, более разупорядоченные углероды могут проявлять подъем сопротивления, когда температура падает. Это является следствием уменьшения плотности носителей при низких температурах, которая доминирует в определяющем сопротивлении таких углеродов.

Что касается углеродных волокон, то экспериментальные исследования показывают, что они также весьма различны по своим электронным свойствам [7]. Так, высокосовершенные волокна имеют кривые сопротивления, приближающиеся к кривой монокристаллического графита, тогда как менее совершенные проявляют поведение, подобное для разупорядоченных углеродов.

Кроме этого, на транспортные свойства углеродных наноструктур сильное влияние могут оказывать различные внешние электрические и магнитные поля.

• 1.    Проводимость бислоя графена во внешнем электрическом поле

Для моделирования электронной структуры бислоя графена целесообразно использовать модель Хюккеля – Хаббарда в рамках метода вторичного квантования, которая учитывает энергию переноса электрона между соседними узлами кристаллической решетки, кулоновское отталкивание двух электронов с противоположными спинами, находящихся на одном узле решетки, межслоевое взаимодействие, а также взаимодействие электронов с внешним электрическим полем [3; 4]. Модель хорошо соответствует представлению об электронах в проводниках, как о Ферми-жидкости.

Внешнее электрическое поле относительно плоскости графена может быть представлено в виде суммы его нормальной ( E_n ) и тангенциальной ( E _τ ) комполент (см. рис. 1).

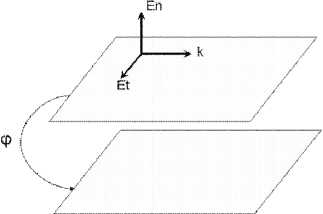
Рис. 1. Схема приложенного электрического поля

Нормальная компонента поля приводит к дополнительному слагаемому в гамильтониане (1):

H = - £ t A ^{( a} 0*7 +A a ⁺ a ⁺ +Aa ^a j a ^{) -} ^ £ a 'a a a ⁺ U £ a a a j a a j -a a j -a j A a                                          J A ct                 J

• —    >t c C⁺ C ■ . + С ⁺ . C ■ I— Ц c 7 С ⁺ C ■ + U 7 С ⁺ C ■ C ⁺ C — Z—T a c jac j +A a cj +A acja P Д^ cjacja 2-1 c jacja cJ -ac j -a

J Aa                                      J Aa                J

• - £ 4 ^{( a} J a c J + a ^{+ c} j+l;a a j a ^{) - вф} £ ^Cj a ^C j a =

a                                 J Aa

• -    У t a ( a t a + a a. )- и ° У a t a .+ и У a t a. a ⁺ a. - Д^ ^A J ^a j ^{jA a}      j ^{jA a} J^a)       Д-, J ^a J ^a Д^ J ^a J ^a j ^{- a} j ^{- a}

  
  

j A a                                          j A a                   j

• ^- £ t A ^{( c j} a ^C j +A a ^{j c +}j JA a c j a H ^ ⁺ eT ) £ ^{C j}a ^C j a ^{j U} £ ^{C j}a ^C j a ^cj- a ^C j- a ^- j Aa                                              j Aa                 j

• - £ t^ ^{( a} J a ^c J + a ^{+ C} j+a ^a j a ⁾ j ξσ

что, в свою очередь, приводит к изменению химического потенциала одного из слоев биграфена на величину вф, где ф - приложенная между слоями разность потенциалов; t _A - интеграл перескока электрона; µ – химический потенциал; U – энергия кулоновского взаимодействия электронов на одном узле, a j _a , a_{j a} , c j _a , c_{j a} - Ферми-операторы рождения и уничтожения электрона со спином о в зонах А и С импульсного пространства соответственно.

Влияние тангенциальной компоненты поля на проводимость образца учитывается через изменение зонной структуры объекта.

Для расчетов использовались следующие значения параметров: U = 10 эВ [6]; E n = 0 ^ 0,3 В/мкм; Е _т = 0 ^ 100 В/мкм.

Из курса статистической физики тензор удельной проводимости в терминах функций Грина [3; 4] определяется формулой Кубо и имеет вид [1; 5]:

σ

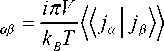
где j α j β – запаздывающая функция Грина для плотностей токов.

Выражая плотности токов через операторы рождения и уничтожения электронов, записывая и решая уравнения движения на двухчастичные функции Грина в представлении Гейзинберга, получаем выражение для удельной проводимости двухслойной наноленты [2]:

a ae = inv £ £ k ( q ) v e ( ^k ) F i + v a ( q ) v e ( k ) F 2 + kT V q , λ k , σ

I                  ch I E ¹ 1+ 1

,

+ ( v a c q ) v c ( k ) + v c ( q■>“„ ( k ) ) F I FL + E i na™-- v ^kT J

^4) ^                 2     £(k)ac    I e a v ’ sh\ — I

V                  v kT J J где k – константа Больцмана; Т – температура; V – объем системы; nac – населенности на разных слоях графена:

n

nca

δε σλ

ac

■JE0 + 4 s ac 2

—

I E i L exp l —1- 1 + 1

V kT J

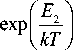
+ 1

Фурье-образы функций Грина, входящие в формулу (3), определяются следующими выражениями:

F 1

= 2

v e^kT + 1

1     "

E ekT +1J

1 1 2 * ( k ) a ) . ch — 1 + 1

kT

sh

2 ε ( k ) ^a

kT V J

F 2

= 2

E ^~ 1 ^c

v e ^kT + 1

1     1

EL ekT +1J

и I 2 ^£ ( k ) c Li ch l---------1 + 1

V kT J

sh

2 ε ( k ) ^c

kT V J

E ,,2 =±V E 22 + 4 s ( k ) ac ² ,

где ε ( k ) ^a , ε ( k ) ^c – дисперсионное соотношение для переходов вдоль слоев, а ε ( k ) ^ac – дисперсионные соотношения для переходов между слоями.

Из рисунка 2 видно, что включение перпендикулярного поля приводит к резкому падению проводимости в области низких температур. Дополнительное приложение тангенциальной компоненты поля приводит к небольшому росту проводимости во всем температурном диапазоне. Однако рисунок 2, б показывает, что в области низких температур (менее 50 К) этот рост более значителен, что приводит к локальному минимуму в температурной зависимости. Дальнейшее увеличение тангенциальной компоненты поля возвращает систему в исходное состояние.

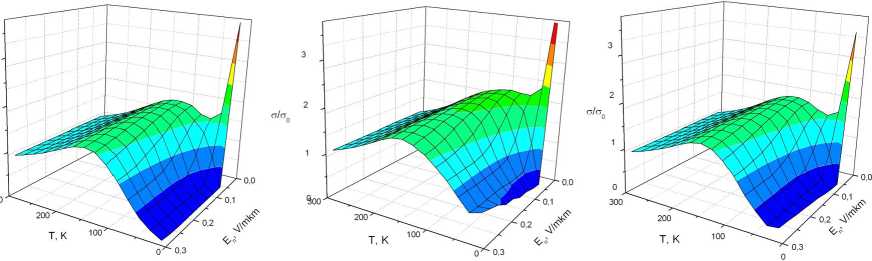
а)                               б)                                   в)

Рис. 2. Зависимость удельной проводимости двухслойной графеновой наноленты шириной N = 5 гексагонов от температуры и нормальной компоненты электрического поля при значениях тангенциальной компоненты:

• а) E _t = 0 В/мкм; б) E _t = 55,2 В/мкм; в) E _t = 101,2 В/мкм

  Периодическое изменение проводимости под влиянием тангенциальной компоненты поля (см. рис. 3 и 4) объясняется изменениями в зонной структуре объекта. С увеличением поля меняется ширина запрещенной зоны по периодическому закону. При нулевой ширине запрещенной зоны наблюдаются максимальные значения проводимости. Период колебаний составляет приблизительно E _τ = 46 В/мкм, а амплитуда порядка σ ₀ = 0,094253 См/м (проводимость для ширины N = 1 гексагон, при температуре 300 К). Таким образом, меняя величину тангенциальной компо-

• ненты электрического поля, можно управлять проводящими свойствами материала, что может быть

использовано при создании новых элементов для микро- и наноэлектроники.

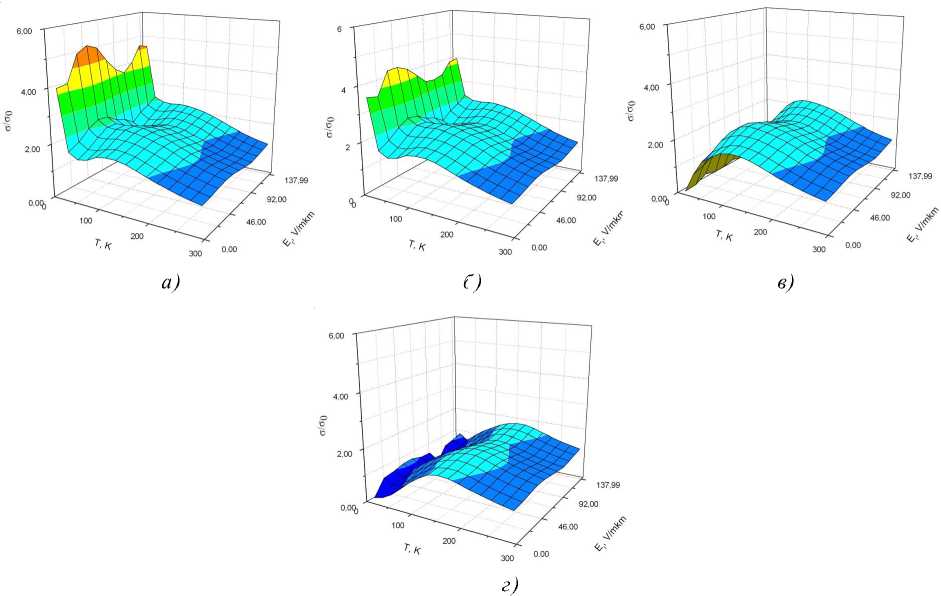
б)

Рис. 3. Зависимость удельной проводимости двухслойной графеновой наноленты шириной N = 5 гексагонов от температуры и тангенциальной компоненты электрического поля при значениях нормальной компоненты:

а) E_n = 0 В/мкм; б) E_n = 0,003 В/мкм; в) E_n = 0,03 В/мкм; г) E_n = 0,3 В/мкм

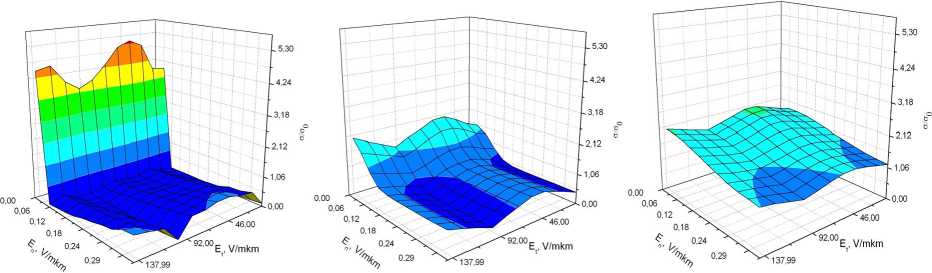
а)                                   б)                                 в)

Рис. 4. Удельная проводимость двухслойной графеновой наноленты шириной N = 5 гексагонов, с учетом внешнего электрического поля при температуре:

а) T = 10 K; б) T = 50 K; в) T = 100 K

Влияние нормальной компоненты электрического поля выражается в сдвиге уровня Ферми в зону проводимости, в результате чего увеличивается количество дважды заполненных состояний, следовательно, уменьшается число носителей заряда в зоне проводимости, что приводит к уменьшению проводимости.

Дальнейший рост проводимости с увеличением перпендикулярной составляющей электрического поля является результатом накопления ошибки округления, при численном расчете проводимости, и не имеет физического обоснования.

Новый эффект выключения электропроводимости двухслойного графена при низких температурах под влиянием внешнего электрического поля дает возможность использовать его как основу для создания нанотранзистора.

С увеличением ширины ленты влияние полей на проводящие свойства ослабевает, и температурная зависимость проводимости стремится к виду, характерному для графита.

Заключение

Влияние нормальной компоненты электрического поля выражается в сдвиге уровня Ферми в зону проводимости, что, в свою очередь, приводит к резкому падению электропроводности в области низких температур (менее 100 К). Полученный эффект может быть использован для создания нанотранзистора на основе двухслойного графена. Влияние тангенциальной компоненты электрического поля в приближении времени релаксации приводит к периодическому изменению проводимости, что объясняется изменениями в зонной структуре объекта. Выявленная закономерность дает возможность создания элементов микро- и наноэлектроники с переменными электронными характеристиками.

ПРИМЕЧАНИЕ

• ¹    Работа проведена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 гг. (Государственный контракт № П892).