Пуринергическая регуляция синаптической передачи фазных и тонических мышц позвоночных

А1 типа, напрямую сопряженных с калиевыми каналами А типа [5]. Эффект аденозина не опосредуется изменением активности Са-каналов, он не снижает амплитуду Са-токов. Ранее мы выявили активность Р 2 Y рецепторов АТФ на пресинапсе озерных лягушек, сопряженных через G i/o подтип ГТФ-белка с системой вторичных посредников, включающих: фосфолипазу С (расщепляет фосфолипиды мембраны), диацилглицерол, протеинкиназу С (встраивает фосфолипазу А2 из цитоплазмы в мембрану), фосфолипазу А2 (фосфорилирует фосфолипиды мембраны), арахидоновую кислоту (расщепляется циклооксигеназой на простагландины Е 2 ) [6].

Методы. Рабочим инструментом явился пакет прикладного компьютерного математического моделирования «Mathcad Professional 2000». Результаты моделирования сравнивались с усредненными экспериментальными данными, полученными в электрофизиологических экспериментах.

• 1.    Моделирование ингибиторного действия АТФ и аденозина в синапсах фазных мышц. АТФ оказывает ингибирующее действие на амплитуду ТКП в синапсах фазной мышцы лягушки (рис. 1). Рассмотрим кинетику действия агонистов на синаптический выброс:

k1              k2k3 m3

P Y + ATP ⇔ P YATP ⇔ ÄÀÃ ⇔ ÏÊÑ ⇒ ÂÂ ↓

• 2                  l1 2              l2l3

k1              k2         k3         k4           k5 k6m6

P Y + ATP ⇔ P YATP ⇔ ÄÀÃ ⇔ ÏÊÑ ⇔ ÔËÀ ⇔ ÀÊ ⇔ ÏÃÅ ⇒ ÂÂ ↓

• ²                  l1 ²              l2            l3             l4            ² l5 l6 ²

k7m7

PY ′+ Adenosine ⇔ PYAdenosine ⇒ ÂÂ ↑

• 1l7

k8k9 m8

PY + Adenosine ⇔ PY ′ Adenosine ⇔ K ⁺ ⇒ ÂÂ ↓

• 1                                l8 1l9

Система кинетических уравнений будет выглядеть следующим образом:

• ^{d [P2YATP]} = k 1 ⋅ a ( t ) ⋅ (1 - [P YATP]) -l1 ⋅ [P YATP]

dt                            22

• ^{d [ДАГ]} = k 2 ⋅ [PYATP] ⋅ (0.5 - [ДАГ]) -l2 ⋅ [ДАГ]

dt

• ^{d [ПКС]} = k 3 ⋅ [ДАГ] ⋅ (0.5 - [ПКС]) -l3 ⋅ [ПКС]

dt

• ^{d [ФЛА2]} = k 4 ⋅ [ПКС] ⋅ (0.5 - [ФЛА ])-l4 ⋅ [ФЛА ]

dt                                       22

• ^{d [АК]} = k 5 ⋅ [ФЛА ] ⋅ (0.5 - [АК])-l5 ⋅ [АК]

dt

• ^{d [ПГЕ]} = k 6 ⋅ [АК] ⋅ (0.5 - [ПГЕ ])-l6 ⋅ [ПГЕ ]

dt                                  22

d [P YAdenosine]

• ¹              = k 7 ⋅ b ( t ) ⋅ (1 - [P YAdenosine]) -l7 ⋅ [P YAdenosine]

dt                                     11

d [P Y ′ Adenosine]

• ¹                = k 8 ⋅ b ( t ) ⋅ (1 - [P Y ′ Adenosine]) -l8 ⋅ [P Y ′ Adenosine]

dt                                     11

• ^{d [K + ]} = k 9 ⋅ [PY ′ Adenosine] ⋅ (0.5 - [K ⁺ ]) -l9 ⋅ [K ⁺ ]

dt ¹

• d[В[В =-m3⋅[ПКС]-m6⋅[ПКС]+m7⋅[PYAdenosine]-m8⋅[K+]+kk⋅(1-[ВВВ dt

• 2. Моделирование облегчающего действия АТФ в синапсах тонических мыщц. В синапсах тонических мышц теплокровных и

• холоднокровных АТФ, в отличие от сохраняющего свой ингибиторный эффект конечного продукта своего распада – аденозина, потенцирует амплитуду вызванных постсинаптических потенциалов – ПСП [2]. Так, при аппликации АТФ в концентрации 100 мкМ амплитуда ПСП мышцы круралис озерной лягушки возрастала до 127±5% (n=6) относительно контроля, в то время как аденозин в той же концентрации снижал амплитуду ПСП до 70±6 (n=6). Неселективный антагонист Р2 рецепторов сурамин и блокатор протеинеиназы С хелеритрин устраняли потенцирующий эффект АТФ на амплитуду постсинаптических ответов синапсов тонических мышц.

Система уравнений решалась методом Рунге-Кутта с фиксированным шагом. Проведенное нами математическое моделирование показало, что наиболее точное воспроизведение амплитудных и временных характеристик опытных данных наблюдается при следующих значениях равновесных констант: k1=0,9; l1=0,5; k2=0,8; l2=0,5; k3=0,7; l3=0,55; k4=0,7; l4=0,75; k5=0,65; l5=0,7; k6=0,5; l6=0,4; k7=0,9; l7=0,87; k8=0,58; l8=0,9; k9=1; l9=1; m3=3; m6=10; m7=0,2; m8=4; kk=1.

Аденозин действует непосредственно на синаптический выброс (А2) или же через активацию калиевых каналов (А1), что отражается на амплитудно-временной характеристике более резким ингибированием выброса, нежели при введении АТФ, влияние которого осуществляется через систему посредников, включающей целый каскад реакций. Хотя каждая реакция эффективно катализируется, в совокупности они приводят к запаздывающему действию агониста.

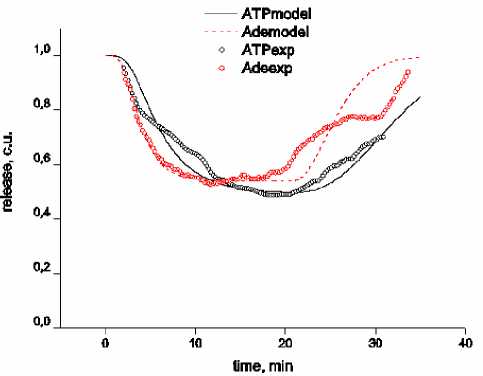
Рис. 1. Кривые действия АТФ и аденозина в концентрации 100 мкМ на амплитуду токов концевой пластинки, полученные в результате эксперимента (exp) и моделирования (model)

Рассмотрим кинетику облегчающего действия АТФ на синаптический выброс, задействующего пресинаптические Р2 рецепторы и протеинкиназу С, в синапсах тонических мышц. По экспериментальным данным изменения амплитуды постсинаптических ответов проведена полиномиальная аппроксимация методом наименьших квадратов. По заданным в дискретные моменты времени ti значениям функции yi(i=1,2,…,n) требуется определить коэффициенты полинома y(t)=a0 +a1t +a2t2 +…+amtm степени m≤n так, чтобы сумма квадратов отклонений экспериментально измеренных значений yi от значений функции y(t) в заданных точках ti была минимальной, т.е. чтобы величина среднеквадратического отклонения

n

• 5 2 = Z( У ( t J - y i )² i = 1

достигала минимального значения. Коэффициенты полинома a0,a1,a2, ,am доставляющие величине δ2 наименьшее значение, находятся из решения системы линейных алгебраических уравнений n    n      nn a 0 ' n + a 1 'Z ti + a 2 'Z ti2 + ... + am 'Z tm = Z Vi i=1                  i=1                            i=1

n    n    nnn a о 'Z ti + a 1 'Z tf + a 2 'Z t3 + ... + am 'Z tm+1 = Z У. ' ti i=1                 i=1                   i=1                            i=1

n    n     nnn m              +1            *m + 2              V^.2 mV''

ti + a 1 'Z ti   + a 2 'Z ti   + ... + am 'Z ti  =Z yi' i=1                   i=1                       i=1                                i=1

На рис. 2 приведены результаты математического моделирования аппроксимации динамики действия АТФ полиномом седьмой степени. Значения коэффициентов аппроксимирующего полинома приведены в таблице 1.

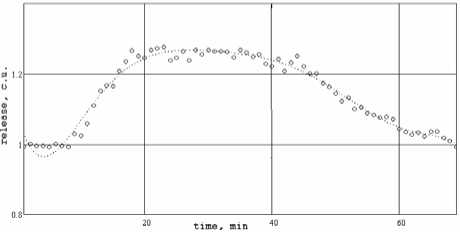
Рис. 2. Точками отмечены экспериментально измеренные значения амплитуды постсинаптических ответов под действием АТФ в синапсах тонических мышц озерной лягушки, непрерывная кривая – аппроксимирующий полином седьмой степени

Выводы: результирующие кривые математического моделирования в общем повторяют экспериментальные данные. Были получены конкретные значения коэффициентов полинома и значения равновесных констант. Поддержано грантом РФФИ.