Путь между двумя пиками ресурса в математической модели миграции животных

Массовые перемещения животных, или миграция, давно привлекают внимание исследователей. Перемещения на различные расстояния обеспечивают животным выживание, рост популяции за счет потребления новых ресурсов. Возникают вопросы, чем объяснить, что в данной среде обитания разные виды показывают различное поведение: одни виды остаются на месте, а другие передвигаются на большие расстояния? Только ли различие в физиологии объясняет мобильность одних и инертность других? Как влияют на миграционные процессы различия в экологии? Является ли экологическая разнородность главной причиной качественного различия в поведении траекторий математической модели популяции?

В статье [1] предпринята попытка ответить на последний вопрос. Предложенная модель описывает миграцию в среде, не зависящей от плотности популяции, где передвижение особей основано на потреблении одного ресурса, который изменяется в пространстве и времени.

Под миграцией понимается крупномасштабное перемещение групп организмов, которое, скорее всего, является откликом на сезонные циклы экологического изменения среды. Математических исследований, посвященных миграции животных, существует достаточно много (см., например, [2]). Но большинство из исследований относятся к стационарной среде. Предлагаемая модель разработана для нестационарной среды, т. е. среды, изменяющейся и в пространстве, и во времени. Известно, что даже простые нелинейные системы с внешним воздействием, такие, как уравнение Дюффинга, могут проявлять хаотическое поведение. Пространственное изменение воздействия еще более усложняет ситуацию.

1.    Математическая модель

Модель, предложенная в [1], используется для исследования влияния сезонных изменений на стратегии пространственных перемещений животных. В этой модели среда обитания содер- жит не истощаемый, не зависящий от плотности популяции ресурс, который по-разному распределен в пространстве и времени. Распределение ресурса не случайно, а периодично по времени. Популяция животных однородна, питается одним и тем же кормом и имеет одни и те же требования к энергетическим затратам при передвижении.

Пусть 0(x, t) - расходресурсана единицу популяции, t - время, x(t) - позиция. Расход ресурса меняется периодически, т. е. 0(x, t) = 0(x, t + T). Пусть также y(x) есть темп использова-dx ния ресурса (затратная функция), зависящий от текущей скорости движения x(t) = —. Предпо-dt лагается, что затраты на движение зависят только от скорости, а не, к примеру, направления, или количества съеденного ресурса.

В математической модели используется эволюционная теория в комбинации с концепцией природных ландшафтов для исследования эволюции. Пригодность (физическая форма) индивидуума после пройденного пути x(t) задается безразмерным числом от

Rd = f [ 0 ( x ( t), t ) - y ( x ( t )) ] e ^{-5 t}dt ,                        (1)

где 5 - относительная значимость краткосрочного прироста ресурса по сравнению с долгосрочным. Наиболее быстрое увеличение показателя R_d обеспечивают стратегии, максимизирующие величину (1).

Каждая особь популяции в любом заданном месте и в любое заданное время «выбирает» начальное условие x(0) и движется согласно скорости x = u(t), где u(t) - выбранная скорость из множества стратегий движения. Оптимальная стратегия u* (t) максимизирует ожидаемую при- годность от

u * = argmax j [0 ( x , t ) - у ( u ( t ) ) ] e - ^{5 t}dt .

u ₀

Ясно, что любое пропорциональное увеличение затрат на движение y (u(t)) может быть компенсировано пропорциональным увеличением расхода ресурса 0(x, t). Для упрощения математических выкладок предполагается, что пространство одномерно, т. е. x(t) и u(t) – ска- лярные переменные.

Гамильтониан текущих затрат имеет вид

H = 0 ( x , t ) - y ( u ( t ) ) + X ( t ) u ( t ),                        (3)

где X(t) вспомогательная функция. Тогда, согласно принципу максимума Понтрягина, для ка- ждого t оптимальная пригодность должна удовлетв орять необходимому условию

u * ( t ) = arg max H = arg max ( X ( t ) u ( t ) - y ( u ( t ) ) ) ,              (4)

uu при условиях

5X (t ) - X ( t ) = , x = u *. d x

В предположении, что y(u) и H(x, X, u) дифференцируемы, из уравнения (4) можно полу- чить

" ( u •) = ^X - y'( u •) = o.

Пока y ( u ) строго выпукла и X мало, будет существовать единственное решение u * уравнения

• (6) . Тогда уравнения (5) можно переписать в виде

  / ( X ),

  
  

  7      ⁵⁰

  X = 5X--

  
  

  d x

  
  

или как равносильное уравнение второго порядка

Y (. x ) x = 5y (. x )--.

5 x

Чтобы определить лучшую стратегию перемещения мы должны задать граничные условия (также известные как условия трансверсальности). Прежде всего, будут отыскиваться случаи, где путь является периодическим с периодом T так, чтобы для каждого решения выполнялись усл овия

x (0) = x ( T ), x (0) = x(T ).                         (8)

Таким образом, математическая модель оптимальной стратегии миграции животных состоит из условия (4), системы (5) (или уравнения (7)) и граничных условий (8).

• 2.    Первичный анализ модели

Если предположить, что функция распределения ресурса может быть представлена как сумма постоянной и периодической компонент

0( x, t) = у (x) + о( x, t),(9)

то можно дать следующую интерпретацию уравнению (7) (см. [1])

( dt J          5x

Это означает, что имеется четыре компоненты, которые характеризуют природу оптимальных стратегий движения:

• •    амплитуда пространственных изменений, которая делится на амплитуду среднего уровня ресурса у и амплитуду сезонного изменения ресурса о ;

• •    коэффициент полезности движения у' ;

• •    относительная значимость краткосрочного прироста ресурса по сравнению с долгосрочным 5 .

Из наблюдений известно, что если пространственные и временные вариации являются независимыми и разделяемыми, то сезонность не влияет на оптимальное перемещение. Также известно, что коэффициент полезности / ' ( x ) (единица стоимости/единица интервала) указывает, что потенциальный масштаб пространственного перемещения ограничен эффективностью перемещения.

С учетом указанных обстоятельств, оптимальные стратегии перемещения могут быть разделены на шесть режимов. Мы приводим схему режимов на рисунке 1.

Долгосрочное планирование (6 - малое)

Краткосрочное планирование (5 - большое)

Сидим на месте

О । рани ченная область Обитания

Факу: 1 ьт аг 11в н ая мн । рация

Дороте движение

1leceзонное

Среднее

Короткие

МИ I ран ИИ

Длинные мшрации

С езонное

'Эффективное движение

'ОТ

Рис. 1

Если передвижение оказывается неэффективным по сравнению с размахом пространственного изменения ресурса, то нет никакой выгоды для перемещения, поэтому особи будут находиться на прежних местах без скоплений (режим 1).

Если затраты на движение малы, то возможность миграций может оказаться реальной. Если при этом сезонное изменение ресурса в пространстве велико по сравнению с его изменением в определенном местообитании, то оптимальная стратегия заключается в следовании за сезонными изменениями ресурса.

Если краткосрочная выгода оказывается важнее долгосрочной (коэффициент 5 достаточно велик), то оптимальная стратегия следует за градиентом ресурса, причем здесь может быть множество региональных непересекающихся миграций, разделенных пустотами ресурса (режим 3).

Если долгосрочная выгода важнее, то существует единственный оптимальный миграционный путь, который может пересекать пустоты ресурса (режим 2).

Если передвижение эффективно и сезонное изменение ресурса мало по сравнению со стационарным, то оптимальная стратегия состоит в передвижении к локальному пику (максимуму) ресурса.

Если значимость краткосрочной выгоды выше долгосрочной, то лучшая стратегия - забраться на самый близкий локальный максимум (режим 5).

Чем меньше коэффициент 5 , тем больше значимость долгосрочной выгоды, и тогда лучше продвигаться к глобальному пику, даже если приходится пересекать пустоты ресурса (режим 4).

Когда сезонные изменения ресурса близки по величине к среднему по пространству изменению ресурса, то структура оптимальных решений может быть очень сложной и нет простых периодических движений, которые обеспечивали бы максимум эффективности (режим 6).

3.    Гетероклиническая траектория

Мы рассматриваем здесь один из возможных типов затратной функции, а именно, квадратичную функцию

Y ( x ) = Y ( u ) = gU- .

Тогда / ' ( u ) = gu , / "( u ) = g и система (5) примет вид

Перепишем (12) как уравнение второго порядка

x = 5 x--

g

’ d x ’

или, после параметризации затрат и распределения ресурса, как

50 x = 5 x - —.                        (14)

d x

Уравнение (14) служит необходимым условием оптимальности.

Будем предполагать, что сезонные изменения ресурса слабы ( ю ( x , t ) ^ 1 ) . Тогда распределение ресурса близко к своей стационарной части ^ (x )

0 ( x , t ) = го ( x , t ) + y ( x ).

Интуиция подсказывает, что оптимальные стратегии должны соответствовать проживанию на пиках ресурса. Если o ( x , t ) мало, или отсутствует, то 0 ( x , t ) ~0 ( x ) не зависит явно от времени и уравнение (14) будет автономным. Его свойства могут быть изучены на фазовой плоскости.

Однако, не все так просто. Во-первых, условие (14) является лишь необходимым, но не достаточным. Это значит, что любой оптимальный путь движения удовлетворяет (14), но не наоборот. Причем, в некоторых случаях оптимального решения может не быть вообще.

Во-вторых, если коэффициент 5 велик, то оптимальная стратегия «следует за градиентом», а если 5 мал, то возникает неоднозначность в выборе лучшего действия в окрестности точки экстремума.

Наиболее интересны случаи, когда функция распределения ресурса имеет два пика. Именно такую ситуацию мы здесь рассматриваем.

Пусть

(x) = a0 - a2x2 (b2x2 + b1 x + b0), где a0, a2,b0,b1,b2 – некоторые заданные числа. Для упрощения вынесем b2 за скобки и пе- реобозначим коэффициенты

• V (x ) = a 0 - a ₂ x ²( x ² + b 1 x + b 0 ).

  
  

Тогда уравнение (14) примет вид x = 5x + 4 a 2 x3 + 3 a 2 b1 x2 + 2 a 2 b0 x.

Сводя его к системе для анализа качественного поведения, получаем

У xc = y y = 2 a 2 b0 x + 3 a 2 b1 x2 + 4 a 2 x3 + 5 y

Здесь может быть одна неподвижная точка, две неподвижные точки, или три неподвижные точки в зависимости от значений параметров. Начало координат всегда является неподвижной точкой, две другие (если существуют) лежат на оси Ox фазовой плоскости xOy и имеют коор- динаты [- 3 b1 + 179b2 -V 8     8

. Можно показать, что при b ₀ <  0 неподвижная точка (0,0)

лежит между двумя другими неподвижными точками. Причем, при a 2 >  0 точки

- ³ b l + 179 b l ² - 32 b 0 ; 0

являются локальными максимумами функции распределения ресурса

v ( x ).

Локальные максимумы имеют, вообще говоря, различные значения и каждый имеет свой бассейн притяжения, характеристики которых управляются коэффициентом 5 . Не всегда существует оптимальный путь от меньшего максимума к большему, он появляется, когда формируется гетероклиническая орбита.

На плоскости параметров b, Ob0 в точках, лежащих ниже параболы b0 = "^b- локальные максимумы соответствуют неподвижным точкам типа седло, в точках выше параболы неподвижная точка лишь одна – начало координат (единственный максимум ресурса). На самой па- раболе b0 = ^bi при каждом фиксированном b, и изменяющимся b0 происходит бифуркация седло-узел, а при b, = 0 - вильчатая бифуркация.

Нас интересует существование гетероклинической орбиты, соединяющей два локальных максимума. Если такая орбита существует, то существует и путь от меньшего максимума к большему. Легко убедиться, что «левый» максимум буд ет больше «правого», если выполнено условие b , >  0. Разность между большим и меньшим максимумами выражается формулой b l ( 9 b ² - 32 b 0 ) ³ .

Численные расчеты показывают, что:

• •    существуют гетероклинические орбиты между двумя максимумами ресурса при b 0 <  0, соответствующие пути от меньшего максимума к большему;

• •    не существует путей, соединяющих локальные максимумы при 0 <  b < - b , ,

• •    управляющий параметр 5 является возрастающей функцией от b , ;

• •    гетероклиническая траектория симметрично отображается относительно оси Ox фазовой плоскости при смене знака b ₁ .

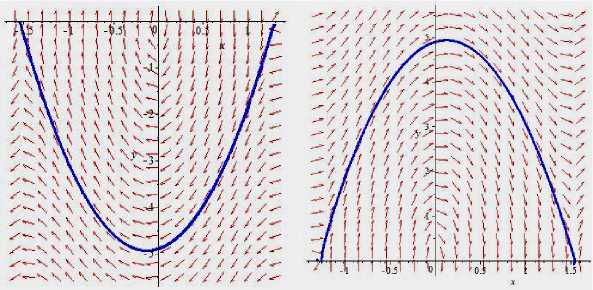
На рис. 2 при 5 = 0,612 представлены две гетероклинические траектории.

Рис. 2. (а) а, = 3, b, = -, b =- 4; (б) а, = 3, b, =- -, b = - 4

2          1 3 0                    2          1        3 0

Заключение

В исследовании путем построения численного решения показано существование гетероклинической траектории между двумя пиками ресурса в модели миграции животных с затратной функцией параболического типа. Определены условия, при которых путь от одного максимума ресурса к другому может осуществиться.