Пути совершенствования методов радиолокационного сопровождения целей

Построение фильтров РЛ сопровождения целей основывается на теории оценивания и фильтрации. При этом в первую очередь принимается во внимание то, как и с помощью каких моделей описываются неизвестные параметры x и их измерения z , а также какая имеется априорная информация о модели вектора x . В радиолокации составляющими вектора x могут являться истинные координаты обнаруженных целей в различных системах координат, а z соответственно их измерения, полученные с помощью РЛС.

Учитывая модели описания неизвестных параметров и их измерений, можно представить следующую классификацию [1]:

• 1)    x – неизвестный детерминированный вектор, z – некоторая известная функция x , причем обращение этой функции невозможно;

• 2)    x – неизвестный детерминированный вектор, z – известная функция x , искаженная шумом измерений;

• 3)    x и z – случайные векторы, имеющие совместное распределение;

• 4)    x – вектор состояния динамической системы, находящийся под воздействием случайного шума, z – вектор выходных сигналов, искаженный шумом измерений.

В зависимости от имеющейся априорной информации о модели вектора x перечислим в порядке увеличения полноты информации функции и параметры, которые могут быть использованы [1]:

• –    функция, описывающая зависимость между векторами x и z ;

• –    дисперсия шума измерений;

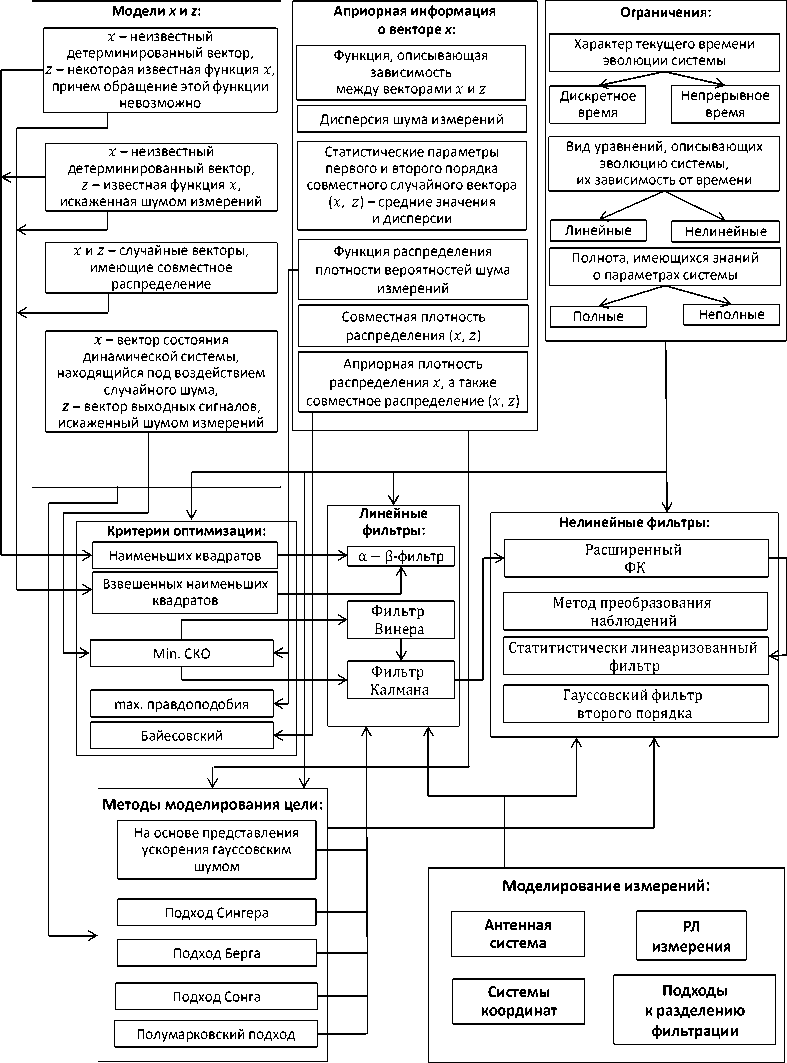
Рис. 1. Схема формирования базового фильтра РЛ сопровождения

• -    статистические параметры первого и второго порядка совместного случайного вектора ( x , z ) - средние значения и дисперсии;

• -    функция распределения плотности вероятностей шума измерений;

• -    совместная плотность распределения ( x , z );

• -    априорная плотность распределения x , а также совместное распределение ( x , z).

Зная априорную информацию о модели цели, а также модели описания неизвестных параметров и их измерений, можно определиться с выбором критерия оптимизации . Приведем их в порядке увеличения полноты информации, с одной стороны, и порядке усложнения оценивателя, с другой стороны [1]:

• -    наименьших квадратов;

• -    взвешенных наименьших квадратов;

• -    минимальной средней квадратической ошибки;

• -    максимального правдоподобия;

• -    максимума апостериорной информации (байесовский).

К примеру, критерии наименьших квадратов и взвешенных наименьших квадратов используются в тех случаях, когда невозможно задать распределение x и z , и имеется весьма ограниченная информация об ошибке измерения. Критерий минимальной средней квадратической ошибки применяется в тех случаях, когда x и z - совместно распределенные случайные векторы. Оценка по критерию максимального правдоподобия формируется только на основании знаний о распределении вероятностей ошибки измерений, и ее значение не зависит от функции плотности распределения вероятностей x , а байесовский критерий может быть использован, если x - случайный вектор с априорно заданной плотностью распределения вероятностей [1].

Также при построении фильтра необходимо учитывать имеющиеся ограничения по таким признакам, как [2]:

• -    характер текущего времени эволюции системы (дискретное или непрерывное время);

• -    вид уравнений, описывающих эволюцию системы (линейные или нелинейные уравнения), а также их зависимость от времени;

• -    полнота имеющихся знаний о параметрах системы (полные или неполные знания).

Наибольшую важность среди указанных ограничений представляет вид уравнения модели движения цели.

Физически адекватные модели движения фрагментов БО - это имитаторы входных данных для разработчиков алгоритмов функционирования информационных средств и их моделей, они является неотъемлемой составляющей общих комплекс -ных моделей космических систем, с использованием которых производятся оценки эффективности информационных систем в различных вариантах их применения [3]. При этом всегда стремятся упростить моделирующие уравнения с минимальным ухудшением точности модели, а следовательно, качество сопровождения [1]. Траектория движения объекта описывается векторной функцией, которая зависит от ряда факторов: типа объекта, его маневренных возможностей, скорости и т.д. На траекторию объекта также влияют случайные факторы: неконтролируемые изменения характеристик среды, в которой происходит движение, различного рода ошибки, возникающие в процессе управления движения объекта, и др. [4].

Теория оптимальной линейной фильтрации основана на гипотезе о точном соответствии моделей динамики состояний системы и измерений исследуемым физическим процессам. Такая априорная информация действительно необходима для создания оценивателя с минимальной дисперсией, поскольку и структура фильтра, и его параметры должны быть строго «настроены» на ожидаемое состояние. Однако на практике столь полными знаниями о модели располагают довольно редко; чаще имеются лишь оценки (с некоторой неопределенностью) статистических характерис- тик шума и начального состояния системы. Кроме того, линейная модель часто является лишь приближенным описанием реальных динамических систем и наблюдаемых процессов. В частности, применительно к проблемам цифровой обработки радиолокационной информации наиболее важным источником неопределенности о движении цели являются непредсказуемые маневры. Как правило, параметры цели (момент начала маневра, его продолжительность и интенсивность) неизвестны. Ускорение обычно учитывается в виде стационарного входного воздействия, хотя такая модель процесса неточно отражает физическую сущность явления. Неопределенность в этом случае заключается в том, что зависимость от времени среднего значения и ковариации процесса ускорения неизвестны. Другим источником неопределенности является наличие нескольких целей или ложных отметок вблизи экстраполированного положения цели. Задача состоит в том, чтобы определить, какая из отметок является истинной, т.е. информация о какой отметке должна объединяться с экстраполированными данными для получения отфильтрованной оценки. Неопределенность здесь связана не со значением неизвестного параметра, а с правдоподобием альтернативных гипотез.

Главной характеристикой маневра являются ускорения. Они бывают двух типов: продольные (приводящие к изменению скорости) и поперечные (изменяющие направление движения).

Независимо от типа используемой системы координат математическая модель движения цели в одном физическом измерении может быть представлена в виде следующих разностных уравнений:

хк+1 = xk + x kT + 0,5 ax/2; (1) xk+1 = xk + ax, kT• где xk, xk - положение и скорость цели при к-м цикле обзора; axk - ускорение цели; Т - период обзора РЛС. Следовательно, при одношаговой экстраполяции траектория цели моделируется с использованием полинома второй степени (по времени) для положения и первой степени - для скорости. Следующим шагом является описание характера ускорения цели. В первом приближении можно принять, что ускорение представляет собой стационарную случайную нормально распределенную переменную с нулевым средним значением и заданной дисперсией. Предполагается также, что ускорение в данный момент времени не зависит от ускорений, имевших место в другие моменты времени [1].

Следует обратить внимание на то, что принятие гипотез о гауссовском распределении и белом спектре ускорений цели обеспечивает непосредственное использование линейного алгоритма. Однако если гипотеза о гауссовском распределении не принята, то соответствующий оптимальный фильтр должен быть нелинейным. Далее, если ускорения коррелированы во времени, то необходимо применять «отбеливающие» процедуры и дополнять вектор состояния. Если процесс ускорения нестационарен, то следует применять более сложные модели цели и соответствующие алгоритмы фильтрации [1].

Кроме моделирования ускорения цели гауссовским белым или коррелированным стационарным случайным процессом используется усовершенствованная модель цели без использования гипотезы о стационарности. В основе предлагаемого подхода лежит полумарковская модель описания маневра цели с дискретизацией возможных ускорений летательных аппаратов. Маневры цели моделируются с помощью полумарковского процесса, т.е. случайного процесса с конечным числом состояний, которые выбираются в соответствии с вероятностями перехода марковского процесса. Полумарковский процесс отличается от марковского тем, что время его нахождения в одном состоянии до перехода в другое само является случайной величиной [1].

ВЕСТНИК РОСНОУ. Серия «Сложные системы…»

В настоящее время используются модели ускорения Сингера, Берга и Сонга:

A cp = Т A ⁺ A m ⁺ w ,                          (²)

где A - истинное ускорение цели; т - интервал корреляции; w - белый шум с нулевым математическим ожиданием; A c m - средняя скорость изменения ускорения.

Эта модель получила дальнейшее развитие и пригодна при описании координированного разворота. Предполагается, что истинное ускорение цели в инерциальной системе координат включает среднее ускорение, обусловленное координированным разворотом, и шум с ограниченной шириной спектра:

1                                A = A c m + v ,                                (3)

где v = + w .

τ

Для построения фильтра также необходимо рассмотреть особенности, составляющие основу для подходов и методов моделирования РЛ измерений (рис. 2.). К таким особенностям относятся:

• -    используемый тип антенной системы;

• -    применяемые в обработке системы координат (СК);

• -    измерительные возможности РЛС;

• -    подходы к разделению фильтрации.

Рис. 2. Особенности моделирования измерений фильтра сопровождения

Используемый тип антенной системы определяет возможности РЛС по адаптивному управлению темпом обновления траектории и сопровождения нескольких целей с использованием перекрывающихся последовательностей импульсов [1]. Различаются:

• –    однопозиционная ФАР;

• –    бистатическая ФАР ;

• –    многопозиционная ФАР.

Сравнение результатов фильтрации в зависимости от указанных антенных систем представлено в [5; 6].

Применяемые в обработке СК имеют свои достоинства и недостатки. Выбор системы координат влияет на точность сопровождения вследствие наличия нелинейностей в уравнениях, описывающих движение цели и датчик измерений. Однако может быть выбрана такая система координат, в которой нелинейности отсутствуют и соответствующее смещение в оценке траектории может быть устранено. Нелинейности тесно связаны с фиктивными ускорениями, которые наблюдаются в некоторых системах координат даже тогда, когда цель движется с постоянной скоростью по прямолинейной траектории [1]. Применяя СК в совокупности или по отдельности, можно добиться упрощения обработки и избавления от возникающих неопределенностей. К тому же выбор СК определяет дальнейшие подходы на этапах функционирования, к примеру методы формирования корреляционных стробов, и подходы к разделению фильтрации, представленные снизу. Самые распространенные в использовании СК:

• –    полярная;

• –    декартова;

• –    смешанная;

• –    ориентированная по курсу цели;

• –    декартова СК, связанная с линией визирования цели;

• –    декартова СК, связанная с РЛС.

На процесс сопровождения цели оказывают существенное влияние способности РЛС по измерениям параметра цели. К широко распространенным дальности, азимуту, углу места дополнительными источниками являются амплитуда принимаемого сигнала и, в особенности, радиальная скорость. Знание радиальной скорости уменьшает время завязки траектории, поскольку для приближенной оценки скорости цели достаточно одной отметки, тогда как при оценивании скорости по измеренным координатам необходимо иметь не менее двух [1]. Информация о радиальной скорости может служить для повышения эффективности алгоритмов сопровождения в случаях завязки траектории, оценивания параметров траектории и в привязывании отметок к траектории [7; 8].

Также для дальнейшего построения фильтра необходимо определиться с подходом по разделению фильтрации (рис. 1). Здесь выбор осуществляется из двух вариантов: или декомпозиция фильтра на три более простых фильтра (по осям координат), или фильтр совместной обработки. Декомпозиция фильтра позволяет упростить обработку, однако такой подход не всегда возможен без снижения точности сопровождения [1; 9].

В зависимости от имеющихся данных, выбранного на их основе критерия оптимизации оценивателя, моделей движения цели и измерений, а также принятых ограничений строится структура фильтра. Наиболее распространенными являются:

• α    – β- фильтр – основывается на критериях наименьших квадратов и взвешенных наименьших квадратов; он обеспечивает как сглаживание, так и экстраполяцию; относится к алгоритмам рекурсивного типа;

фильтр Винера и фильтр Калмана – основываются на критерии минимальной средней квадратической ошибки; первый используется, если процессы не зависят от времени, последовательность поступающих данных не ограничена, а фильтры стационарны и работают в установившемся режиме; это приводит к формированию фильтра с постоянными параметрами. При втором, калмановском, подходе могут решаться нестационарные задачи при конечном интервале наблюдений; такой подход приводит к синтезу нестационарного фильтра, при этом выражения для оценки сигнала и ее ковариации имеют форму рекурсивных разностных или дифференциальных уравнений в зависимости от дискретного или непрерывного характера исследуемых вопросов [2; 10].

Линейная модель часто является лишь приближенным описанием реальных динамических систем и наблюдаемых процессов, в то время как нелинейная более адекватно отображает реальные процессы [11]. Развитие нелинейной фильтрации весьма важно для формирования РЛ алгоритмов сопровождения, поскольку во многих случаях зависимость между данными измерений и динамическими параметрами цели имеет нелинейный характер. Задача оценивания состояния нелинейной системы может рассматриваться как распространение среднего квадратического способа на динамический случай. Все существующие нелинейные оцениватели имеют субоптимальный характер.

Расширенный фильтр Калмана. Представляет собой нелинейный субоптимальный алгоритм, основанный на том, что нелинейные функции перехода состояний системы, то есть перехода состояний в результате воздействия входных сигналов и отображения состояний системы в результаты наблюдений, до статочно гладкие, такие функции могут быть разложены в ряд Тейлора и аппроксимированы членами ряда невысоких порядков.

Метод преобразования наблюдений. Он основан на задании процесса линейным уравнением, а связи процесса с наблюдениями – нелинейным. В этом случае формируется фильтр, состоящий из нелинейного процессора без памяти, за которым следует обычный калмановский фильтр.

Статистически линеаризованный фильтр. Применяется, когда аппроксимация с помощью ряда Тейлора невозможна. Применение статистической линеаризации приводит к формированию нелинейного субоптимального фильтра, имеющего структуру, определяемую калмановским фильтром для линеаризованной модели.

Гауссовский фильтр второго порядка. При этом подходе в разложении нелинейностей в ряд Тейлора учитываются первые и вторые производные. При линейном уравнении измерений этот фильтр преобразуется в обычный калмановский фильтр, а при отбрасывании производных второго порядка – в расширенный калмановский фильтр.

Рассмотренные алгоритмы в соответствии с их сложностью и эффективностью можно представить в следующем порядке: расширенный калмановский фильтр реализует простейший алгоритм и дает хорошие результаты при умеренных нелинейностях и невысоком уровне шума; гауссовский фильтр второго порядка обеспечивает более высокое качество фильтрации за счет усложнения алгоритма; наконец, метод статистической линеаризации позволяет добиться хороших результатов в различных случаях применения, однако требует больших вычислительных затрат. На практике для выбора наиболее подходящего алгоритма для конкретного применения необходимо проведение сравнительного анализа по критерию «стоимость – эффективность» [1].

Эффективность применения рассмотренных подходов, методов и алгоритмов фильтрации в значительной степени определяется особенностями конкретной решаемой задачи.

Заключение

Рассмотрев кратко изложенные принципы, методы построения фильтров РЛ сопровождения, нетрудно заметить, что на современном этапе широко используются субоптимальные фильтры, разработанные для выполнения прикладных задач, причем строгие решения на практике не реализуемы. Пути совершенствования методов РЛ сопровождения связаны с синтезом различных подходов, с разработкой методов получения дополнительной информации о наблюдаемых системах, моделей взаимосвязи этих систем и результатов их измерений, сужения или расширения имеющихся ограничений, разработкой новых или усовершенствованием имеющихся критериев оптимизации оценивателей и построением на основе новых исходных данных базовых фильтров сопровождения. Далека от завершения и теория адаптивной фильтрации, пути совершенствования которой представляются в синтезе различных подходов адаптации, а также в разработке алгоритмов последовательного и параллельного применения различных подходов и построения на этих основах новых адаптивных фильтров.