Qualitative and Quantitative Evaluation of EEG Signals in Epileptic Seizure Recognition

Published Online May 2013 in MECS

• I.    Introduction

  Epilepsy is a brain disorder that is characterized by sudden and recurrent seizures. Epilepsy can cause abnormal electrical activity in the brain and may alter consciousness, perception, sensation, behavior and body movement. Patients experience varied symptoms during seizures depending on the location and extent of the affected brain tissue. Most seizures are very brief and is rarely life threatening. Depending on the extent of the involvement of brain areas during the epilepsy, it can be divided into two main types that according to the International League Against Epilepsy (ILAE), in 1981, includes: 1- Generalized seizures that involve almost the entire brain, 2- Partial (or focal) seizures that originate from a circumscribed area of the brain and remain restricted to that area [1]. Generalized seizures

can be divided into several main types, such as Absence, Atypical Absence, Myoclonic, Clonic, Tonic, Tonic-clonic, and Atonic seizures. In addition, Partial seizures can be divided into three main types such as Simple partial, Complex partial, and Secondarily generalized seizures.

Due to a large number of patients in intensive care units (ICU) and the need for continuous observation of such conditions, several methods for epileptic seizure recognition have been developed in the past. Several quantitative system approaches incorporating statistical techniques, dynamical systems and optimization for brain disorders [2]. In assessment of epilepsy, brain activity plays a central role. Electroencephalography (EEG) is a technique, which contains much information about the patient’s psycho-physiological state [3]. Therefore, EEG has become the premier diagnostic method for epilepsy recognition. EEG can be recorded in two essential ways: The first and most common is non-invasive recording known as scalp recording. The second is invasive recording that often is known as inter-cranial EEG. Frequency bands of EEG signals are interesting to be interpreted such as delta (1 -4 Hz), theta (4-8 Hz), alpha (8-13 Hz), beta (13-30 Hz) and gamma (> 30 Hz).

In principle, there are two different scenarios of how a seizure could evolve. It could be caused by a sudden and abrupt transition, in which case it would not be preceded by detectable dynamical changes in the EEG. Such a scenario would be conceivable for the initiation of seizures in primary generalized epilepsy. Alternatively, this transition could be a gradual change in dynamics, which could in theory, is detectable. This type of transition could be more likely in focal epilepsies. About dynamical states of epileptic EEG signals, there are some main classic states of inter-ictal, pre-ictal, ictal, and post-ictal; but clinical and laboratory experiments leave little doubt that a pre-seizure period exists in temporal lobe and perhaps other forms of epilepsy. Its existence, however, raises fundamental questions about what constitutes a seizure, what brain regions are involved in seizure generation, and whether discrete inter-ictal, pre-ictal, ictal, and post-ictal physiologies exist, or blend together in a continuous process [4].

A lot of research has been undertaken in assessment of epilepsy over the last few years. Gotman [5] presented a computerized system for recognizing a variety of seizures, in year 1982. Murro et al. [6] developed a seizure recognition system based on the discriminant analysis of the EEG signal recorded from the intracranial electrodes. Choosing suitable features is important for seizure recognition. Many features have been investigated based on time domain and frequency domain [7,8], wavelet transformation [9,10], Fourier Transformation [11], energy distribution in timefrequency plane [12], and chaotic features [13-17]. Subasi [9] used a method for analysis of EEG signals using discrete wavelet transform (DWT) and classification using an ANFIS. Non-linear features of EEG signals have also often explained complex structure of epilepsy [18,19]. Kannathal et al. [16] have shown the importance of various entropies for recognition of epilepsy. Adeli et al. [20] presented a wavelet-chaos methodology for analysis of EEGs and delta, theta, alpha, beta, and gamma sub-bands of EEGs for recognition of seizure. Ghosh-Dastidar et al. [21] presented a wavelet-chaos-neural network methodology for classification of EEGs into healthy, ictal, and inter-ictal EEGs.

From studies reported in the literature, EEG signals can be considered chaotic. In this research, an approach based on Adaptive Neuro-Fuzzy Inference System (ANFIS) was presented for the seizure recognition. The main aim of this research is to produce a multi-aspect combination of chaos and ANFIS for epileptic seizure recognition using EEG signals.

• II.    Methods and Materials2.1    Database

  For studying epilepsy, the subjects that are used are either human o animal. EEG signals used for this research are obtained from Bonn University, Germany, which is available in public domain [22]. The complete datasets consists of five sets of data (denoted A – E ), each containing 100 single-channel EEG segments. Each segment has N =4096 sampling points over 23.6 seconds. All EEG signals were recorded with the same 128-channel amplifier system and 12 bit A / D resolution, which the sampling rate of the data was 173.61 Hz, which it have the spectral bandwidth of the acquisition system is between 0.5 to 85 Hz. These segments were selected and cut out from continuous multi-channel EEG recordings after visual inspection for artifacts such as muscle activity, eye movements etc. Sets A and B have been recorded from external surface EEG recordings of five healthy volunteers in the wake state with eyes open and eyes closed, respectively. Sets C , D and E have been recorded from depth electrodes EEG recordings from five patients. Sets A and B have been recorded during normal state. Set D were recorded from within the epileptogenic zone (Inter-ictal period), and those in set C from the hippocampal formation of the opposite hemisphere of the brain (Inter-ictal period). Set E has been recorded during seizure activity (Ictal). Figure 1 shows the sample recordings of EEG signals obtained from five sets A - E . For a more detailed description of the data, please refer to the [22].

• 2.2    Features Extraction

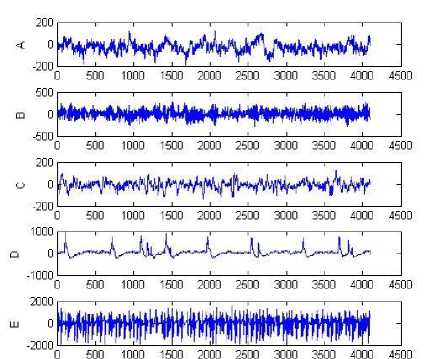
Fig. 1: Sample recordings of A , B , C , D and E dataset from top to bottom

Choice of the methods and measures for discriminating dynamical changes of epileptic signals highly depends on the characteristics of epileptic EEG signals, on the other hand, regarding type of seizure, specifications of individuals who data are recorded from them etc, are important parameters that have significant effect on results of recognition and classifying of epileptic EEG signals.

In this research to concentrate on the recognition of dynamic changes of EEG signals recording, a short epoch of data is selected. The time series of data are divided into 2 seconds epochs with an overlap of 1 second.

Non-linear and chaotic measures have received the most attention in comparison with the measures mentioned before such as time domain, frequency domain, time-frequency etc.

• 1)    Hurst exponent

  The name Hurst exponent (H) derives from Harold Edwin Hurst in 1951 [23]. The Hurst exponent is

directly related to the Fractal dimension. a small Hurst exponent has a higher fractal dimension and vice versa. Brownian walks can be generated from a defined Hurst exponent. H has a value between 0 and 1 (0 ≤ H ≤ 1). If a value H in the range 0.5 <  H < 1, the random walk will be a long-term memory process (or positive correlated time series or persistent). A value H in the range 0 <  H < 0.5 can indicate anti-correlated time series (anti-persistent). A value of H = 0.5 can indicate a completely uncorrelated time series.

Hurst exponent are shown in Figures 2, 3 and 4 corresponding to the A , C and E data, respectively.

g :^ ж ®

о

|   9 H is the slope of th^ linear fit ~ 0.3967 |

„15________________i________________i________________i________________i________________i________________i________________i

' 0          1          2         3         4         5         G          7

°9И

Fig. 2: Hurst exponent of the EEG signal corresponding to normal time series ( A ).

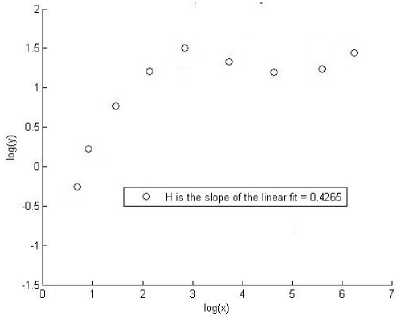
Fig. 3: Hurst exponent of the EEG signal corresponding to inter-ictal time series ( C ).

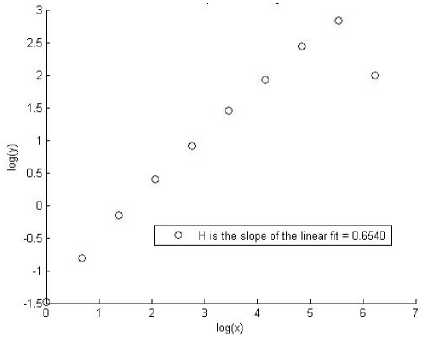
Fig. 4: Hurst exponent of the EEG signal corresponding to ictal time series ( E ).

From the above Figures 2, 3 and 4 it is clear that the value of Hurst exponent for non-epileptic signal sets A , B is less than epileptic signal set E .

• 2)    Lyapunov exponent

• 2.3 Classification

  The Adaptive Neuro-Fuzzy Inference System, first introduced by Jang in 1993 [24,25]. The ANFIS is a fuzzy Sugeno model put in the framework of adaptive systems to facilitate learning and adaptation [24]. Jang showed that even if human expertise is not available it is possible to intuitively set up practical membership function and employs the neural training process to generate a  set of  fuzzy IF-THEN  rules that

The lyapunov exponents have been proven the useful dynamical quantity for the chaotic system analysis [25]. Lyapunov exponents define the average exponential rates of divergence or convergence of the nearby orbits in the phase space and can be estimated using largest lyapunov exponent (λ).

A negative lyapunov exponent indicates that, the orbit attracts to a stable fixed point (or stable periodic orbit). A lyapunov exponent of zero indicates that, the orbit is a neutral fixed point (or an eventually fixed point). A positive lyapunov exponent indicates that, the orbit is unstable and chaotic. Lyapunov exponent is shown in Figure 5 corresponding to the A , C and E data, respectively.

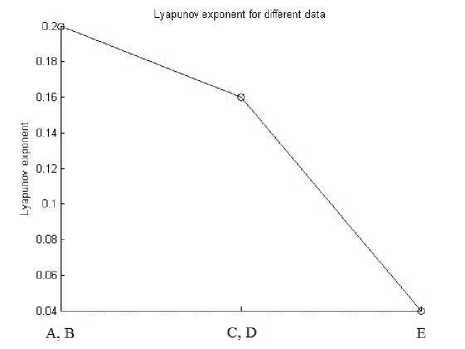
Fig. 5: Plot of λ values for EEG signals between three different classes.

From the above Figure, it is clear that the value of Lyapunov exponent for epileptic signal set E , is less than non-epileptic signal sets A , B .

Approximate a desired data set [24]. In this structure, there are five layers in the overall network framework, including the fuzzification layer, product layer, normalization layer, defuzzification layer and the total output layer.

• III.    Computation Results and Analysis

The process of EEG analysis consists of two states: first the qualitative analysis and second the quantitative analysis of EEG signals.

The qualitative results are presented in this section. The value of Hurst exponent for non-epileptic signal sets A , B is less than epileptic signal set E . In addition, the value of Lyapunov exponent for epileptic signal set E , is less than non-epileptic signal sets A , B . The reduce in λ value , and the increase in H value to mean the reduction in brain system complexity for subjects with seizure state, therefore the number of the necessary dynamic equations for the description of the brain state in the seizure state decreases.

The quantitative results and comparison with the other researchers presented in this section. As shown in Table. 1, we designed three experiments to test the ability of our classifier to separate: 1- Normal EEG (sets A and B ) vs. inter-ictal EEG (sets C and D ) 2- Normal EEG (sets A and B ) vs. ictal EEG (set E ) 3- Inter-ictal EEG (sets C and D ) vs. ictal EEG (set E )

Table 1: The classification accuracy for three experiments

Number	Experiment	Classification accuracy (%)
1	Normal vs. inter-ictal	97.4
2	Normal vs. ictal	96.9
3	Inter-ictal vs. ictal	96.5

The classifier is validated using 4-fold cross validation on 400, 300 and 300 samples, respectively, in experiments 1, 2 and 3.

In experiment 1, the accuracy using inter-ictal EEG for epileptic recognition reaches 97.4%. In experiment 2, the accuracy using ictal data reaches 96.9%. In experiment 3, 96.5% accuracy shows our system can distinguish ictal vs. inter-ictal EEG.

For A - E or A , B - E classification, the result obtained from our method is better than [16] and [9]

researches with 7.4% and 3.4% difference to discriminate EEGs, respectively. For A , B , C , D - E classification, the accuracy obtained from [1] is better than [12] with 0.04% difference.

• IV.    Conclusion

This research has presented the analysis of the EEG signals for the characterization of the epileptic behavior of the brain activity. We investigated the chaotic dynamics underlying the EEG in patients with Epilepsy’s disease by non-linear analysis to understand the role of chaos in brain function. Therefore, presents a novel method for epileptic seizure recognition using chaotic features and ANFIS classifier. We calculated the hurst exponent and largest lyapunov exponent for non-linear analysis of EEG signals. The process of EEG analysis consists of two states: first the qualitative analysis and second the quantitative analysis of EEG signals. The reduce in λ value and the increase in H value to mean the reduction in brain system complexity for subjects with seizure state, therefore the number of the necessary dynamic equations for the description of the brain state in the seizure state decreases. Therefore, chaotic features could be helpful to distinguishing between epileptic EEG and normal EEG. This method is evaluated using a benchmark EEG dataset, and qualitative and quantitative results are presented. Our inter-ictal EEG based diagnostic approach achieves 97.4% accuracy in 4-fold cross validation. Diagnosis based on ictal data is also tested in ANFIS classifier, reaching 96.9% accuracy. Therefore, our method can be successfully applied to both inter-ictal and ictal data. We show that non-linear analysis can provide a promising tool for detecting relative changes in the complexity of brain dynamics, which may not be detected by conventional linear analysis. The testing performance of the model diagnostic system is found to be satisfactory and we think that this system can be used in clinical studies in the future after it is developed.

Acknowledgments

The authors would like to acknowledge Dr. R.G. Andrzejak of Bonn University, Germany, for providing permission to use the EEG signals available in the public domain.