Quantum algorithmic gates: nanotechnology design and application in intelligent control

КВАНТОВЫЕ АЛГОРИТМИЧЕСКИЕ ЯЧЕЙКИ: ПРИМЕНЕНИЯ В ПРОЕКТИРОВАНИИ В НАНОТЕХНОЛОГИЯХ И В ИНТЕЛЛЕКТУАЛЬНОМ УПРАВЛЕНИИ

Бархатова Ирина Александровна1, Фукуда Тошио2, Джиованни дели Антонио3, Хагивара Тахико4, Ризотто Джиани5, Порто Массимо6, Ямафуджи Кадзуо7, Ульянов Сергей Викторович8

• ¹Аспирант;

ГБОУ ВО «Международный Университет природы, общества и человека «Дубна»,

Институт системного анализа и управления;

141980, Московская обл., г. Дубна, ул. Университетская, 19;

• ²Доктор наук, профессор;

Факультет микросистем, механики и информатики;

Нагоя университет;

Япония, Нагоя, Фуро-чо, Чикуса-ку;

• ³Доктор наук, профессор;

Поло дидаттико, Крема, факультет информационных технологий;

Виа Браманте, 65-26013, Крема, Италия;

• ⁴Доктор наук, профессор;

Yamaha Motor Europe N.V.;

Поло дидаттико, Крема, факультет информационных технологий;

Италия, Виа, Крема, Браманте, 65-26013.

• ⁵Доктор наук, профессор;

ST Microelectronics;

Италия, 20041 Agrate Brianza, Via C. Olivetti, 2;

• ⁶Доктор наук, профессор;

ST Microelectronics;

20041, Италия, Agrate Brianza, Via C. Olivetti, 2.

• ⁷Доктор наук, профессор;

Факультет механики и технической кибернетики (интеллектуальные системы),

Университет передачи информации;

1-5-1, Япония, Токио, Chofu, Chofugaoka ,182;

• ⁸Доктор физико-математических наук, профессор;

ГБОУ ВО «Международный Университет природы, общества и человека «Дубна»,

Институт системного анализа и управления;

141980, Московская обл., г. Дубна, ул. Университетская, 19;

Many of the most popular models of quantum computation are direct quantum generalizations of well known classical constructs [1 – 3]. This includes quantum Turing machine, gate arrays and walks. These models use unitary evolution as the basic mechanism of information processing and only at the end do we make measurements, converting quantum information into classical information in order to read out classical answer. In the more familiar gate array model computational steps are unitary operations, developing a large entangled state prior to some final measurements for the output.

Just two ideas from quantum computing (and some algorithmic ingenuity) are considered. The first of two ideas is amplitude amplification. The second idea is that any classical (either deterministic or probabilistic) computation can be simulated on a quantum computer. More precisely, (i) in the circuit a classical model, a classical circuit with N gates can be simulated by a quantum circuit with O ( N ) gates; (ii) if the query model (when only the number of queries is counted), a classical computation with queries can be simulated by a quantum computation with N queries.

Thus, this greatly simplifies description of quantum algorithms. Instead of describing a quantum algorithm, we can describe a classical algorithm that succeeds with some small probability e . Then, we can transform the classical algorithm to a quantum algorithm and apply the amplitude amplification to the quantum algorithm. The result is a quantum algorithm with the running time or the number of queries that is times the one for the classical algorithm with which we started. A similar reasoning can be applied, if instead of a purely classical algorithm, we started with a classical algorithm that involves quantum subroutines. Such algorithms can also be transformed into quantum algorithms with the same complexity.

Another approach in quantum computing consists in the formalism of the measurement based on quantum computation. In this case we start with a given fixed entangled state of many q-bits and perform computation by applying a sequence of measurements to designated q-bits in designated bases. The choice of basis for later measurement may depend on earlier measurement outcomes and the final result of the computation is determined from the classical data of all the measurement outcomes.

In contrast to unitary evolution, measurements are irreversibly destructive, involving much loss of potential information about a quantum state’s identity. Thus it is interesting, and at first sight surprising, that we can perform universal quantum computation using only measurements as computation steps.

Two principle schemes of measurement based on computation are teleportation quantum computation and so-called cluster model of one-way quantum computer. From another standpoint, the appeal of hidden variable theories is that they provide one possible solution to the measurement problem. For example, even if an observer is placed in coherent superposition that observer would still have a sequence of definite experiences, and the probability of any such sequence could be calculated. For this case hidden variable theory is simply a way to convert a unitary matrix that maps one quantum state to another into a stochastic matrix that maps the initial probability distribution to the final one in some fixed basis.

A hidden variable theory can be based on networks flows: if we examine the entire history of a hidden variable, then we could efficiently solve problems that are believed to be intractable even for quantum computers. By sampling histories one could, for example, search an unordered database of N items for a single

«marked item» using only O N ³

database queries. By comparison, Grover’s quantum search algorithm requires 0

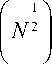
queries, while classical algorithms require 0 ( N ) queries.

Remark. The readers unfamiliar with asymptotic notation, O ( f ( N ) ) means «at most order f ( N ) », Q ( f ( N ) ) means «at least order f ( N ) » and 0 ( f ( N ) ) means «exactly order f ( N ) ».

The results are surprising is that, given a hidden variable, the distribution over its possible values at any single time is governed by standard quantum mechanics and is therefore can be efficiently simulated on a quantum computer. So when examining the variable’s history confers any extra computation power, then it can only be because of correlations between the variable’s values at different times. Quantum computation explores the possibilities of applying quantum mechanics to computer science.

If built quantum computers would provide speed-ups over conventional computers for a variety of problems. The two most famous results in this area which are Shor’s quantum algorithms for factoring and finding discrete logarithms and Grover’s quantum search algorithm show that quantum computers can solve certain computation problems significantly faster than any classical computers. Shor’s and Grover’s algorithms have been followed by a lot of other results.

Each of these algorithms has been generalized and applied to several other problems. New algorithms and new algorithmic paradigms (such as adiabatic computing which is the quantum counterpart of simulated annealing) have been discovered. We can explore several aspects adiabatic quantum-computational model and use a way that directly maps any arbitrary circuit in the standard quantum-computing model to an adiabatic algorithm of the same depth.

Many quantum algorithms are developed for the so-called oracle model in which the input is given as an oracle so that the only knowledge we can gain about the input is in raising queries to the oracle. As our measure of complexity we use the query complexity. The query complexity of an algorithm A computing a function F is the number of queries used by A . The query complexity of F is the minimum query complexity of any algorithm computing F . We are interested in proving lower bounds of the query complexity of specific functions and consider methods of computing such lower bounds.

The two most successful methods for proving lower bounds on quantum computations are the following: the adversary method and the polynomial method. An alternative measure of complexity would be to use the time (temporal) complexity which counts the number of basic operations used by an algorithm. The temporal complexity is always at least as large as the query complexity since each query takes one unit step, and thus a lower bound on the query complexity is also a lower bound on the temporal complexity.

For the most of existing quantum algorithms the temporal complexity is within poly-logarithmic factors of the query complexity. One barrier to better understanding of the quantum query model is the lack of simple mathematical representations of quantum computations. While classical query complexity (both deterministic and randomized) has a natural intuitive description in terms of decision trees, there is no such easy description of quantum query complexity.

The main difference between the classical and quantum case is that classical computations branch into non-interacting sub computations (as represented by the tree) while in quantum computations, because of the possibility of destructive interference between sub-computations, there is no obvious analog of branching. The bounded-error model is both relevant to understanding powerful explicit non-query quantum algorithms (such as Shor’s factoring algorithm) and theoretically important as the quantum analog of the classical decision tree model.

We are interested in studying classical and quantum complexities because an oracle sometimes gives a separation between them. For example, there was shown one problem where we needed exponentially many queries in the bounded error classical case, but only a single query is needed in the quantum case. Another occasion to study a query complexity is when a temporal complexity is hard. In such case the number of queries we make gives a lower bound for the temporal complexity.

In fact, currently there is no lower bound method for quantum temporal complexity that gives superlinear bounding, and by studying quantum query complexity, we get lower bounds heuristic on quantum temporal complexity.

One of the powers of quantum computation comes from the fact that we can query in superposition. That is, if we are given a set of n elements from 1 to n , we can query an oracle in parallel once to obtain a superposition of f ( 1 ) through f ( n ) . However, we can in a sense only learn one of the f ( i ) 's from such a query. The real power of quantum computation comes from interference. It means that the information in the state, e.g., f ( i ) ’s, can be combined by means of unitary quantum gates in non-trivial way and we can extract a global property of the input.

We present results of different approaches for solution of the partial problems of QA simulation in the Table below.

The core of any QA is a set of unitary quantum operators or quantum gates. In practical representation quantum gate is a unitary matrix with particular structure. The size of this matrix grows exponentially with the number of inputs, making it impossible to simulate QAs with more than 30–35 inputs on classical computer with von Neumann architecture.

Table. Effectiveness of different approaches of QA simulation

Approaches	Hardware implementation	Maximum qubit number	Time requirements for one step, sec
Based on decomposed parallel computations (Niwa, Matsumoto and Imai, 2002)	Sun Enterprise 4500, В 400Mhz processors, 10GB memory, 64 bit OS	29+1	395,81
Software approach based on matrix concatenation (Hsu, 2002)	PIV1.7GZ, 1Gb, Linux, Matlab	22+1	44,6
QuIDD1 based approach (quantjDh/0208003)	Dual AthlonMP 1.2GHZ.1GB, C++	19+1	<1
Hardware approach (YMC-ST, 2001)	Analog circuit	3	«1
Hardware approach (YMC-ST.2002)	Analog circuit. Surface Mount Devices	6	«1, on the way
Software approach with operator matrices (YMC.2000)	PHI, 800MHz, 512MB, Matlab, Windows 2000	11+1	1500
Software approach with vectorized algorithms (YMC.2002)	Pill, 1GHz, 512MB, Matlab, Windows 2000	23+1	50

1 — QuIDD — Quantum Information Decision Diagram

We present four practical approaches to design fast algorithms to simulate most of known QAs on classical computers:

• -    Matrix based approach;

• -    Algorithmic based approach, when matrix elements are calculated on «demand»;

• -    Problem-oriented approach, where we succeeded to run Grover’s algorithm with up to 64 and more q-bits with Shannon entropy calculation (up to 1024 without termination condition);

• -    Quantum algorithms with reduced number of operators.

The first approach is based on the direct representation of the quantum operators. This approach is more stable and precise, but as a drawback it requires allocation of operator’s matrices in the computer’s memory. Since size of the operators grows exponentially, practically this approach is applicable for simulation of QAs with small number of input q-bits (no more than 11 on PC). Using this approach it is relatively simple to simulate excitations on QA and to perform fidelity of analysis.

The second approach, we call it also fast quantum algorithm simulation, is more advantageous. It doesn’t require the allocation of operator matrices in PC memory, but it calculates each component when it is required. In this case the number of inputs with this approach has two bounds: (i) the first bound is due to exponential grow of operations required to calculate the result of the matrix product; and (ii) the second bound is that state vector is still must be allocated in computer memory.

Using this approach it is possible to simulate up to 19 q-bits on PC and even more on a system with vector architecture [Imai et al, 2002] (see the Table). This and other approaches are described.

Furthermore, due to particularities of the memory addressing and access processes in the PC, when number of q-bits is relatively small, this approach is faster than approach with direct matrix allocation. The main difficulty of this approach is a requirement of the advanced study of the quantum operators, and of their structure. Also with this approach it is more difficult to simulate external excitations and to perform fidelity analysis of the simulated algorithm.

The third is a problem-oriented approach is a result of the advanced study of the concrete QA structure and state vector behavior. For example in Grove’s QSA, the state vector always has only two different values: (i) one value corresponds to the probability amplitude of the answer; and (ii) the second one corresponds to the probability amplitude of the rest of the state vector. Using this assumption it is possible to apply the algorithm only to these two numbers, and simulate its behavior. In this case the only limit is a representation of the floating-point numbers, necessary to simulate actual values of the probability amplitudes.

Remark. Note that after superposition operation, these probability amplitudes are very small ( ^ ). We succeeded to run Grover’s QSA with this approach simulating 1024 q-bits without termination condition calculation and up to 64 q-bits with termination condition estimation based on Shannon’s entropy.

For other QAs maximum number of input q-bits will be smaller, since probability amplitudes have more complicated distribution. Also introduction of an external excitation will decrease the possible number of q-bits to the same range with second approach.

The fourth approach is applicable to the control QAs, where in one embodiment, entanglement and interference operators could be bypassed (or simplified), and result is computed based only on superposition of the initial states (and deconstructive interference of final output patterns) representing the state of the designed schedule of control gains.

Another example is a particular case of Deutsch-Jozsa’s and Simon’s algorithms when entanglement is absent by using of pseudo-pure quantum states.

Since acceleration of the QA calculation is a very important computer science problem one of the parts of this book is dedicated to basic concepts of quantum computing and quantum algorithms comparative analysis of the temporal complexity of the known QAs. Another part gives the introduction of the generalized approach in QA simulation and information analysis of quantum operators. The third part describes the structure of representation of the QAs applicable to low level programming on classical computer (PC). The forth part is a generalization of the approaches and introduction of the general QA simulation tool based on algorithmic representation of quantum operators for fast problem-oriented QAs. The fifth part is an introduction to fast quantum algorithms design. The sixth part reports a general software/hardware approach in acceleration of QC and classically efficient quantum algorithm simulation and a general comparison of the developed approaches in QA simulation.

Fig. 1 summarizes the known approaches to QA design and simulation.

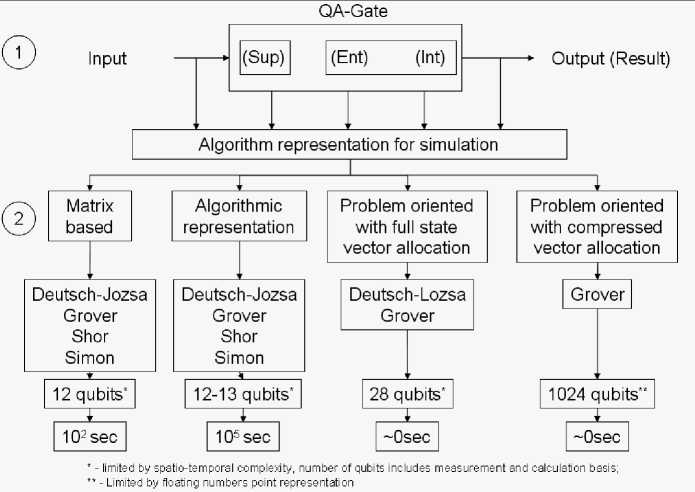
Figure 1. Different approaches for QA simulation (sup – superposition, ent – entanglement, int – interference operators)

The high level structure of the quantum algorithms can be represented as a combination of different superposition entanglement and interference operators. Then depending on algorithm, one can choose corresponding model and algorithm structure for simulation. Depending on the current problem, one can choose (if it is available) one of the simulation approaches, and depending on approach one can simulate different orders of quantum systems.

For computer science the problems of error correction codes and visual cryptography are introduced. As Benchmarks of intelligent control engineering the problem of robust control of essentially nonlinear control objects as autonomous robots in unpredicted control situations are presented.

In present paper we are concentrating our attention on the description of the classically efficient simulation of QAG based on fast quantum algorithms, its physical limits and information bounds and trade-offs. Software and hardware implementations of the developed fast quantum algorithms are described.

Recently, the interest to the design of quantum algorithmic gates started to grow rapidly. According to the Science Citation Index , by the beginning of this century more than 500 papers were published annually in the cited journals. The reader can judge the state-of-the-art in this area by the papers published in the collected translations and collected articles cited in References. Studies on the quantum computers represent one of the important applications.

Applications of QAGs design and simulation to study of Benchmarks in AI, computer science and control engineering problems are considered from effective simulation on classical computer. In AI as Benchmark the problems of knowledge self-organization for intelligent control are discussed in following papers of this journal.