Quantum defect and common fractions

Quantum defect and common fractions

The common fractions N1/N2, where N1 and N2 – the small integers, quite often are used at the quantum-mechanical consideration of microcosm objects (for example, fractional charges of quarks and some quantum characteristics, such as particles spin).

Recently the fractional quantum Hall effect was discovered, and common fractions have considerably expanded their presence in microcosm physics.

The theory of the fractional quantum Hall effect has appeared nontrivial, so the Nobel Prize on physics in 1998 was awarded not only for discovery of the effect in 1982 (Daniel Tsui and Horst St ӧ rmer) but also for the theory creation in 1983 (Robert Laughlin).

And now one more sensational discovery: common fractions were «detected» at the analysis of experimental characteristics of hydrogen-like atoms and ions (with only one electron on an outer shell). It has appeared, that the effective main quantum number of outer shell electron, that is, subject to quantum defect (Rydberg correction), can be expressed in common fractions.

The main quantum number n of hydrogen atom can be defined directly from the formula for electron energy [1]

E =

me4 1

2 h ² n ^2.

However hydrogen-like atoms with only one external electron have very complex spectra. In particular, in [1] (§68) we find the following reasoning:

«Other atoms have states reminding hydrogen. It is a question of highly excited states in which one electron possesses greater main quantum number and consequently is at essentially greater distance from the atomic core. Such electron movement can be considered, in some approach, as movement in Coulomb field of the atomic core with unit effective charge. Values of energy levels, however, appear too inexact, and it is necessary to make the correction taking into account a deviation of a real field at small distances from ideal Coulomb field».

«… we can conclude that the expression for energy levels is to be changed by replacement of the radial, that is, of the main quantum number n on (n + Δ_i) , where Δ_i - is some constant (so-called Rydberg correction):

4 л

„ me 1

E =----у •

2h2 (n + AJ2

Rydberg correction does not depend (by the definition) on n , but is, certainly, the function of azimuthal quantum number l of electron (which we attribute to Δ in the form of an index), and also depends on moments L and S of atom as a whole. When L and S are fixed, Δ_i rapidly decreases with increase of l . The more is l , the less is the time which electron spends near atomic core and that is why levels of energy should come nearer and nearer to hydrogen».

Rydberg correction (quantum defect) is determined empirically, while its theoretical calculation meets with great difficulties.

However in the last few years the analysis of the experimental data stored during previous decades has shown [2], that effective main quantum numbers of external electron n* = (n + Δ _i) , that is, subject to quantum defect, appear close to values of common fractions n* ≈ N₁/N₂ , where N₁ and N₂ – the small integers.

Let's consider in detail this experimental law using characteristics of atoms and ions with only one external electron in not excited state. In this case external electron is most close to the atomic core and its influence on electron movement is particularly great.

Actual (effective) number n* of hydrogen-like atoms, proceeding from (2), can be expressed in terms of ionization potentials:

n* =

/ X 1/2

113,61

к Vi 7

•

Here φ_i - ionization potential of considered atom, 13,6 eV – ionization potential of hydrogen atom.

In more general case of hydrogen-like ion with the charge of

atomic core ze formula (3) takes the form:

n* =

(13,6z2 )1/2

к Vi 7

•

Formula (3) evaluation (using the known experimental data φ_i [3]) is shown in table 1. Common fractions most close to n* are shown Ibid:

N 1

N 2

Where N₁, N₂ – the small integers got by trial-and-error procedure.

As it was stated above, the table 1 presents characteristics of not excited state of the single external electron of atoms.

Table 1

Atom	Li	Na	K	Cs	Rb	Ag	Pt	Nb	Fr
φ i , eV	5,39	5,138	4,339	3,893	4,176	7,574	8,96	6,88	3,98
n*	1,588	1,627	1,770	1,869	1,805	1,340	1,232	1,406	1,849
n* ≈	19/12	13/8	23/13	15/8	9/5	4/3	16/13	7/5	24/13
N 1 /N 2	(1,583)	(1,625)	(1,769)	(1,875)	(1,80)	(1,333)	(1,231)	(1,40)	(1,846)

For selection of concrete values of the numerator and the denominator of common fractions (5) it is convenient to use auxiliary table 2.

In the table N₂ limitation up to 13 inclusive was accepted.

Under each value of denominator N₂ (from 2 up to 13) in columns there are values of fractions N₁/N₂ within the limits from 1 to 2, used to determine common fraction nearest to each concrete experimental value of the main quantum number.

As an example in table 2 red color marks out values of common fractions most close to values of effective main quantum numbers n * , presented in tab. 1.

Similar characteristics of hydrogen-like ions with the core charge equal to two and three electron charges ( z=2, z=3) , calculated in accordance with the formula (4), are presented in tables 3 and 4.

In spite of the fact that some values n* in tables 3 and 4 exceed 2, auxiliary table 2 also can be used, as at increase in numerator N₁ , obviously, there is a periodic increase of fraction N₁/N₂ by unit, so that corresponding decimal digits are repeating itself.

Table 2. Values of common fractions n=N 1 /N 2 within the limits 1≤n≤2 , when N₂ ≤13 .

2	3	4	5	6	7	8	9	10	11	12	13
1	1	1	1	1	1	1	1	1	1	1	1
1,5	1,333333	1,25	1,2	1,166667	1,142857	1,125	1,111111	1,1	1,090909	1,083333	1,076923
2	1,666667	1,5	1,4	1,333333	1,285714	1,25	1,222222	1,2	1,181818	1,166667	1,153846
	2	1,75	1,6	1,5	1,428571	1,375	1,333333	1,3	1,272727	1,25	1,230769
		2	1,8	1,666667	1,571429	1,5	1,444444	1,4	1,363636	1,333333	1,307692
			2	1,833333	1,714286	1,625	1,555556	1,5	1,454545	1,416667	1,384615
				2	1,857143	1,75	1,666667	1,6	1,545455	1,5	1,461538
					2	1,875	1,777778	1,7	1,636364	1,583333	1,538462
						2	1,888889	1,8	1,727273	1,666667	1,615385
							2	1,9	1,818182	1,75	1,692308
								2	1,909091	1,833333	1,769231
									2	1,916667	1,846154
										2	1,923077
											2

Table 3

Ion (z=2)	Be+	Mg+	Ca+	Sr+	Ba+	Cd+	Ra+	Fe+	La+
φ i , eV	18,21	15,03	11,87	11,026	10	16,904	10,144	16,18	11,43
n*	1,728	1,902	2,141	2,221	2,332	1,794	2,316	1,834	2,182
n* ≈	19/11	19/10	15/7	20/9	7/3	9/5	30/13	11/6	24/11
N 1 /N 2	(1,727)	(1,9)	(2,143)	2,222	(2,333)	(1,8)	(2,308)	(1,833)	(2,182)

Table 4

Ion (z=3)	B++	Al++	Sc++	Y++	In++
φ i , eV	37,92	28,44	24,75	20,5	28
n*	1,797	2,075	2,224	2,444	2,091
n* ≈ N 1 /N 2	9/5 (1,8)	27/13 (2,077)	20/9 (2,222)	22/9 (2,444)	23/11 (2,091)

But then quite natural question arises: whether the numbers presented in table 2 locate too densely on a number axis and consequently whether we deal here with random coincidence of fractional numbers with corresponding experimental values n* ?

To check up this assumption, all the set of fractional numbers of table 2 was sorted in ascending order. Further, this sequence of numbers was presented in the form of a rising curve with the markers corresponding to these numbers, and experimental values of the main quantum numbers were represented in the form of the horizontal lines crossing this curve.

In fig. 1 such visual representation of characteristics of atoms with the only one external electron in nonexcited state, recited in tab.1, is shown.

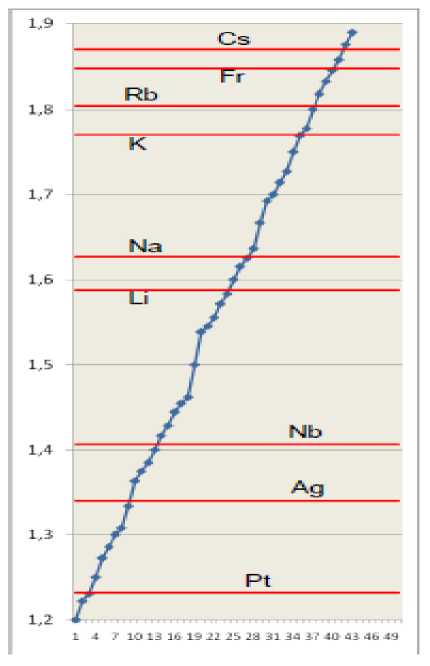
Fig.1. Effective main quantum numbers of hydrogen-like atoms (tab. 1) are shown as horizontal lines. Common fractions ( N₂ ≤ 13) are represented as markers on a rising curve (tab. 2).

Visual data representation, really, has appeared an effective tool to prove a nonrandom character of the discovered experimental law.

On the other hand, it became clear, that limitation N₂ < 13 is quite sufficient for such analysis.

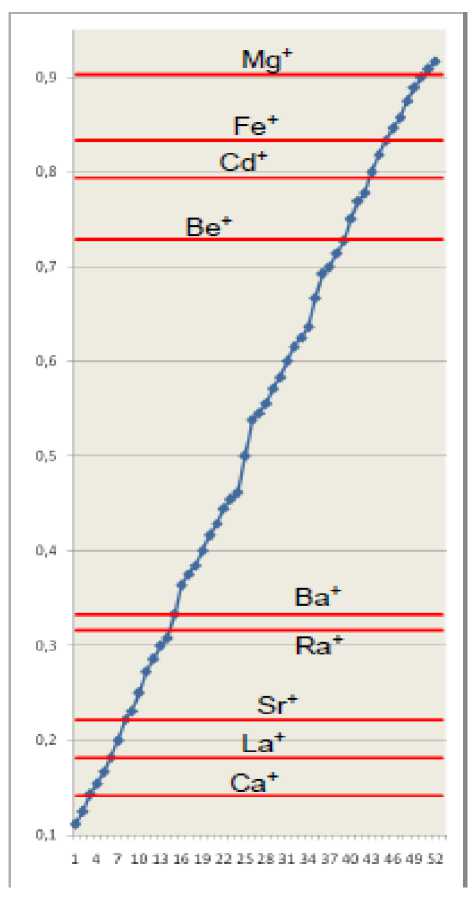
Fig.2. Effective main quantum numbers of hydrogen-like ions ( z=2, tab. 3 ) are shown as horizontal lines. Values of common fractions ( N₂ < 13) are represented as markers on a rising curve. Integer parts of numbers are omitted.

As limitation on denominator N₂ determines the density of distribution of fractions values on a numerical axis, and increase of N 1 just periodically increases value of N 1 /N 2 by unit, so on fig. 2 and subsequent figures only fractional parts of numbers are shown (the whole parts of numbers are omitted).

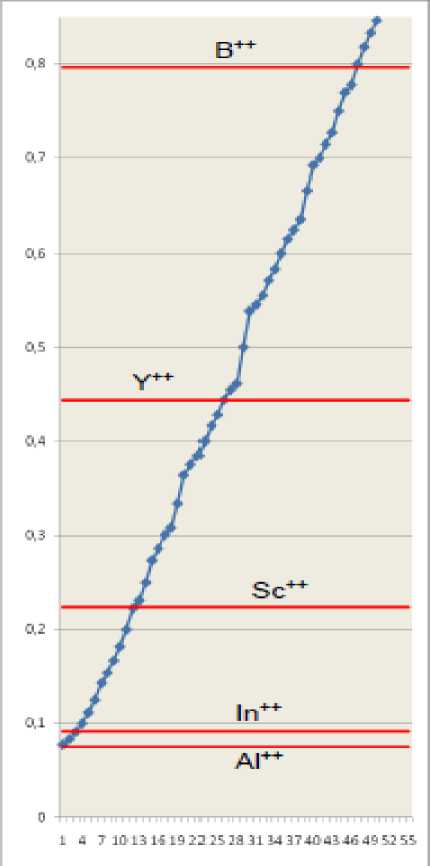
Fig.3. Effective main quantum numbers of hydrogen-like ions ( Z=3, tab. 4 ) are shown as horizontal lines. Values of common fractions ( N₂ < 13) are represented as markers on a rising curve. Integer parts of numbers are omitted.

Let's notice that visual data representation and use of auxiliary tab. 2 has given an opportunity to correct some common fractions correlated in earlier work [2] with effective main quantum numbers of «hydrogen-like states».

For additional check of the discovered experimental law characteristics of some others hydrogen-like ions, including ions with great degree of ionization, have been analyzed.

Results of these calculations are presented in tab. 5, 6 and fig. 4, 5.

Table 5

Ion	Si+++	P++++	S+++++	Cl++++++	J++++++	Ar+++++++
z	4	5	6	7	7	8
φ i , eV	45,13	65,01	88	114,2	104	143,4
n*	2,196	2,287	2,359	2,416	2,531	2,464
n* ≈ N 1 /N 2	11/5 (2,2)	16/7 (2,286)	26/11 (2,364)	29/12 2,417	33/13 (2,538)	32/13 (2,462)

Table 6

Ion	Hg+	Sn +++	Pb+++	Sb ++++	Bi++++	Te +++++	Po+++++	Xe +++++++
z	2	4	4	5	5	6	6	8
φ i , eV	18,751	46,4	39	63,8	56	83	73	126
n*	1,703	2,166	2,362	2,308	2,464	2,429	2,59	2,628
n* ≈ N 1 /N 2	17/10 (1,7)	13/6 (2,167)	26/11 (2,364)	30/13 (2,308)	32/13 (2,462)	17/7 (2,429)	31/12 (2,583)	21/8 (2,625)

As it was before, characteristics of hydrogen-like ions with most different degrees of ionization confirm the affinity of effective main quantum numbers of the single external electron to values of common fractions N₁/N₂ with rather small denominator ( N₂ ≤ 13).

Visual representation of these ions characteristics against the background of common fractions sequence with all evidence has confirmed not random character of experimental law under study.

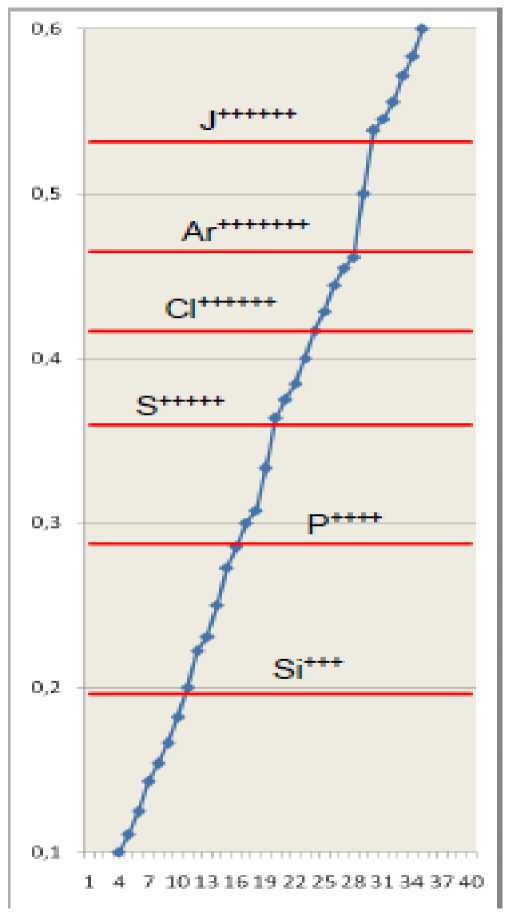
Fig.4. Effective main quantum numbers of hydrogen-like ions (tab. 5) with most different degrees of ionization are shown as horizontal lines. Values of common fractions ( N₂ ≤ 13) are represented by markers on a rising curve. Integer parts of numbers are omitted.

It is necessary to emphasize especially, that as well as any law of nature, the discovered property of «hydrogen-like states» can have exceptions (as it, for example, takes place in Mendeleev periodic table), and in addition various degree of accuracy at experimental check turns up. But such «deviations» do not cancel the law; on the contrary, it stimulates further researches as it actually always was in physics progress over the last decades.

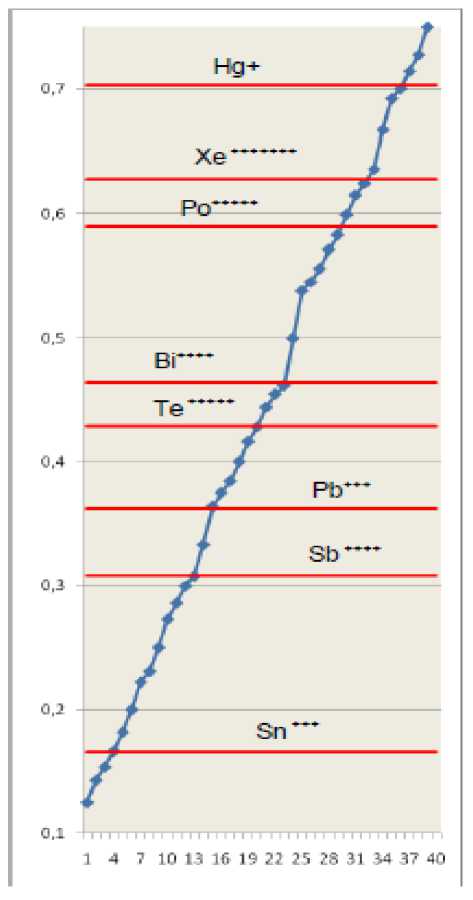
Fig. 5. Effective main quantum numbers of hydrogen-like ions (tab. 6) with a different degree of ionization are shown as horizontal lines. Values of common fractions ( N₂ ≤ 13) are represented by markers on a rising curve. Integer parts of numbers are omitted.

The discovered experimental law has caused many assumptions in regard to its physical nature and provoked discussion on possible atom theory progress.

We intentionally do not mention here any considerations about the possible physical mechanism of the described phenomenon and consequences for the theory development; we limit us only to the analysis of experimental data so that not to distract the reader from the subject in fact.

However the discovery of the not known before atoms and ions property, connected with features of interaction of external electron with the core, undoubtedly, is one of the most important events in the modern atom physics.