Quantum-dot Controlled Electronic Block Triggering a Quantum Computation Procedure

Published Online April 2020 in MECS

Quantum computers are physical devices performing logic operations with quantum states by unitary transformations, which do not break quantum superpositions during computations. Quantum computer operates with states. A system with two probable states is the simplest and closest analog of the classical bit-based system. The term “q-bit” (qubit – quantum bit of information) was suggested to denote the state of such quantum two-level system. A search for physical processes occurring at both atomic and molecular levels, which would eventually provide performing of logic operations similar to those in classical computers, is a fundamental stage on the way to quantum computer creation. Thus, the progress in quantum computer development depends upon our knowledge on the structure and dynamics of multielectron quantum systems (atomic and molecular).

The idea of quantum computers has been first put forward by R. Feynman in his works published in the middle eighties of the twenty century [1, 2]. It was based on a conclusion that memory and operating speed of classical computers are insufficient to solve quantum tasks. This fact can be illustrated by the following example. An n -particle system with two states with halfinteger spins has 2ⁿ basic states. While solving the particular problem one should write to the computer memory 2ⁿ of these states amplitudes as well as carry out the corresponding computations. Since n can be arbitrarily large the number of states to be operated on may also be very large. As a result the computations will face insuperable obstacles. Reasoning from this negative result Feynmann assumed that quantum computers would probably possess some features enabling quantum problems to be solved. In addition to the aforesaid it is pertinent to add that the creation of quantum computers is tightly connected with the problem of existence noncalculated functions and the related problem of algorithmically unsolvable tasks. These problems have been thoroughly investigated in the works of Yu. Manin [3].

We should stress here that at the present time the application of quantum computers (if they were created) could be effective not only for the solution of quantum physics problems. The last fifty years of the development of natural sciences were marked by appearance of new braches of knowledge, such as nonlinear optics, open system physics, and quantum information. We must also mention here a new branch of science being originated at the border of several disciplines. It deals with the field of knowledge studying the structure and dynamics of molecules. In a broad sense one can speak about the investigations of matter on molecular level. The aim of such investigations is electron and spatial structure of multielectron (molecular) systems as well as the nature of processes and phenomena occurring with these systems participation. Appearance of new fields of investigations has promoted to the formulation of new tasks which solution required new computational devices. Among these tasks there are tasks of quantum chemistry.

The work has the following structure. The second section of the manuscript is devoted to justification of visualization of states associated with a system of information quantum bits (q-bits). Such visualization or materialization allows each of the 2n quantum states to be associated with a specific element of an electronic device. In our case, this element should be a nano-trigger formed from two-dimensional graphene material. Then these elements are combined into an appropriate scheme capable of performing the computation process. In this section, a non-linear process that can control the operation of such an electronic device is also described. To this end, it is proposed to employ a special device created on the basis of a quantum dot and operating according to the principle of self-organization. A quantum dot formed from a compound, the molecules of which are characterized by intramolecular rearrangement, so-called valence tautomerism. This section also deals with creation of a reversible logic block (Toffoli gate) capable of performing logical operations. The third section entitled “A block-diagram of a quantum device based on a visualized massif of q-bit states” is devoted to the description of a specific block-diagram that can ensure quantum computation using graphene nanotriggers. In this case, emphasis is placed on the description of Toffoli three-q-ubit gate composed of three nanotriggers, one of which should play the role of a q-bit of a target state or computation output. The paper ends with a conclusion and list of references.

• II.    The Historical Aspect of the Problem of Quantum Computer Creation

Just after R. Feynman's pioneer works highlighting urgency of the quantum computer creation as well as after publication of Yu.P. Manin’s monograph, in which a problem of noncomuptable functions and the related algorithmically insoluble tasks is discussed in detail , a number of theoretical works on the specified topic has been performed. They resulted in numerous publications including reviews and monographs (see, for example, reviews [4-7] and the literature cited therein). Theoretical breakthrough in the solution of a problem of quantum computers was based on ideas about physical processes, which would ensure the realization of the logical operations similar to those occurring in classical computers. It was supposed that employment of specifics of quantum objects will allow improving the computation procedure, but will not change essentially its essence. It seemed that the necessary conditions, which should provide successful experimental realization of R. Feynman’s ideas, were eventually found. Moreover, the landmark Shor's work [8] has specified the scope of real tasks, which could be solved only with employment of quantum computers. Conviction in fast creation of quantum computers was strengthened in 1998 when it was reported on realization of elementary quantum algorithm based on two q-bits using nuclear magnetic resonance (NMR) phenomenon. In one work, nuclear spins of hydrogen atoms (protons) were used, and in other paper hydrogen and carbon nuclear spins were studied [9, 10]. Within the next few years a series of works aimed at the increase of the number of NMR qubits in the elementary quantum processor has been performed. For example, in 2001 it has been reported on quantum NMR processor containing seven qubits. This processor made in possible to realize (only in elementary variant) the Shor algorithm. The processor performs logic operations with seven spins: two carbons (13C) and five fluorine (19F) atoms. The molecule of perfluorobutadienyl iron complex acted as an elementary processor [11]. We should also note here a series of works performed by J.A.Jones and his team dedicated to experimental methods of realization of the operations with NMR-qubits, including such operations as NMR quantum cloning [5].

To illustrate the performance potential of a quantum computer it is reasonable to refer to the well-known scheme of the classical computer operation which can be represented as a sequence of three operations: 1) input of the initial data into the computer register; 2) performance of computations; 3) output of the results. The first stage of the classical computer operation could be compared with preparation of the initial state of the quantum computer. This means creation of a devise (similar to the register of the classical computer) containing quite large number of quantum objects which are located in the entangled states [4, 6].

According to the laws of quantum physics, if the system consists of n two-level q-bits, its state generally represents a superposition of 2n basic state, i.e. (the standard designations are used here [6]):

n - 1

ψ = ∑ _{i = 1} a i ψi ) (1)

If to use rather small number (n = 102) of q-bits, it is possible to receive rather large

2N = 2100 ≈ 1030

mathematical information resource of the quantum computer. From here follow the main advantages of the quantum computer. Really, in the course of recording a number containing n figures, the amount of cells occupied from the total number equaling 1030, will be just n figures. Other (unoccupied) cells can be used for performing the parallel computations.

Here it should be stressed that these cells are not specific elements of schemes or magnetic sites (domains), which are used for recording the necessary information. They are referred to eigenvalues of the operator of the physical characteristics describing the system of q-bits which, according to the laws of quantum mechanics, can be determined with a probability. In certain sense it is a question of a big set of virtual (in terms of availability) cells, the application of which is far from to be obvious. This is one of fundamental problems. Further, after the information (for example, digital) will be entered into these cells, they need to be operated somehow to perform the computation operations. And, at last, it is necessary to find a way to output the result after finishing the computations. This creates fundamental difficulties, which should be overcome in the course of quantum computer design.

The most of the researches performed so far involve the search for suitable individual quantum objects. At the same time it is assumed that an opportunity of creating the computing quantum schemes on the basis of such object is an obvious fact. Figuratively speaking, what is meant here is the trying to find a solution following "bottom to up ideology ". Very impressive results have been obtained in this area (see, for example, works [1219] and the references given therein). Consequently, the problem of quantum computer creation has been theoretically studied in detail. Moreover, some researchers believe that this problem can become a routine in essence. The main criteria, to which should satisfy the devices capable of quantum computations, have been found [20]. But the quantum computer is a macroobject, which should operate in a macroworld. Therefore an alternative approach, "top to down", becomes possible. According to this approach, creation of devices, suitable for quantum computations, is based on application of initial systems of many particles. Note that over the last forty – fifty years, the huge amount of new compounds with the most diverse spatial and electronic structure, and, therefore, with the most various physical and chemical properties has been synthesized and investigated.

Ensuring the corresponding functioning of q-bits is not the end in itself. The main thing in creation of the quantum computer relates to application of quantum states of q-bits in the organization of the computation procedure. But if it so, then taking into account the existing difficulties in selection of q-bits, it is reasonable to create a priory system from necessary amount of quantum objects (quantum dots or islets) accounting also entangled quantum states, which would visualize all states equaling to 2n.

From the aforementioned follows the first and, perhaps, the most important problem in the creation of the quantum computer. This is visualization or materialization of the above states. Only after reaching this goal, one can speak about the first stage of the quantum computer operation, i.e. about entering (recording) digital information into the register of the classical computer. Also, it must be kept in mind that visualization should not change reality, i.e. q-bits should remain quantum character of their states.

In conclusion of the analysis of publications on the problem of creating a quantum computer, we can only ascertain the achievement of certain experimental successes in the implementation of the idea of R.

Feynman. However, the possibility of real quantum computations in practice is still to be proved.

• III.    Visualization of Q-bit State Massif

At this stage, the real quantum computer represents an additional block, which is built in already existing modern computers. In such a device, the computing process is performed according to the laws of quantum physics. It is clear that the corresponding peripheral devices are not mandatory in the quantum processor, which performs directly mathematical operations. Selection of q-bits system and ensuring their operation is not the end in itself. The main thing in creation of the quantum computer relates, eventually, to application of quantum states of the q-bit massif in the organization of the computing procedure. As to implementation of quantum computation procedure, the process, when each materialized (visualized) Shor's cell would correspond to an element of the electronic scheme is supposed to be the most natural. Then such elements are united in the corresponding scheme capable of performing the computation procedure. Both elements of this scheme and the scheme itself should operate according to the laws of quantum physics. Being a real quantum system, such a device performs real computation procedures similar to classical computer, but at the level of microworld. It is appropriate to emphasize that the proposed here is an electronic device is not a true quantum state computer option in the literal sense of the word. The possibility of its creation – a reflection of the progress in the study of micro-and nanoworld, which achieved over the past twenty years, i.e. after justification of the idea of the quantum computer.

It is a common knowledge that the main element of the modern (classical) computer is the processor, which actually ensures functioning of the computer, i.e. the procedure of computation and its control. The processor operates on the basis of electronic schemes, which main element is the trigger. The latter can play a role of the binary place holder. A set of the united triggers allows creating blocks (registers), necessary for successful operation of the processor. The amount of the created triggers is set generally by number n from expression 2, which, in turn, is defined by tasks to be solved. Thus, such devise can be, in principle, planned with all that it implies.

The following explanation is appropriate here. Graphene became the first representative of a new class of materials, two-dimensional crystals. Uniqueness of graphene electronic properties is caused by the fact that its charge carriers are similar to zero-mass relativistic fermions and are described by relativistic Dirac equation, but not by the Schrödinger equation. Thus, it is possible, in particular, to investigate all nuances and variety of quantum electrodynamics in solid phase. Graphene is of fundamental interest owing to its unique electronic properties. Near the Fermi level, electrons in graphene possess linear dispersion, and the energy band gap between valence and conductivity zones is absent.

Therefore, electrons can be described by the twodimensional Dirac equation for zero-mass particles.

A possibility of the Dirac equation application for this purpose has been proved Wallace in 1947. But only after separate graphene layers were successfully isolated, it became clear that graphene can be used for study of new type of the particles, zero-less charged quasi-particles. Such properties of these particles as two-dimensionality, spinor nature, zero mass and absence of the gap in the spectrum lead to a number of the electronic phenomena, which do not have analogs in other physical systems. As for the application issue, graphene is of special interest for design of nanoelectronic devices. Two-dimensional structure of graphene warrants an absolute limit of miniaturization, at least, in one dimension that ideally matches to modern planar technologies for the creation of integrated circuits. Nanolithographic technique allows cutting out arbitrary shaped fragments from graphene for installation of contact and contactless electrodes. Besides, from graphene sheet various structures with the superperiod can be formed (for example, depositing the ordered layer of adatoms on grapheme sheet or making periodically located holes), which can have interesting properties. Mobility of charge carriers in pure samples of graphene reaches record high values and almost does not depend on concentration that also is valuable to possible applications [21].

On a basis of the above-stated one can assume that the trigger is created from graphene ribbons of 10 nm wide [22]. In this case, it will occupy the area of about 5•10-14 m-2. Therefore, about 1010 nanotriggers can be placed on one square centimeter. These are those quantum objects, which should play a role of q-bits, i.e. bits of the quantum computation. The principal moment in application of the graphene nanotrigger for implementation of the elementary computing procedure is that this trigger should operate according to the laws of a microworld, i.e. the laws of quantum physics. This goal can be reached using self-organization approach. Here the following explanation should be done.

Such a possibility could be evaluated as follows. Let the dependence of deviation amplitude f ( x ) on the initial state x is defined by the expression:

f(x) = ax — bx ” ,              (3)

where a and b are constant positive coefficients, n > 2 . If x « 1, then bx ” « ax, therefore

f(x) « ax.                  (4)

Thus, in the case of ( 4 ), f ( x ) grows linearly with growth of x. If x value is comparable with 1 , it would be impossible to neglect the bx n member, since for the description of the system behavior one should use the initial Equation ( 3 ). Hence, the growth of function deviation at the expense of ax member will cause nonlinear limitation owing to the deduction of bx n value. Under several x values, the f ( x ) function will be close again to zero and all starts from the beginning.

The system will automatically regulate itself, as its properties depend on a current state (in this case―from x value). Therefore, it is reasonable to conclude that by somehow changing the given molecular system, it is possible to achieve (in principle) the necessary values for the corresponding parameter (or parameters). Obviously, such changes could be carried out by three ways:

• 1)    the introduction of new atoms to molecular structure;

• 2)    the external action (for example, applying an electromagnetic field);

• 3)    the combination of these two ways.

The fundamental problem is to understand what molecular objects can be suitable for similar manipulations. Based on the most general ideas, one can assume that here one should deal with the compounds where characteristic intramolecular interactions will ensure the realization of the required (from a position of a problem discussed here) quantum states. These are the compounds containing atoms with unfilled 3 d - , 4 f - and 5 f - shells. In solids, such atoms retain localized magnetic moments completely or partially. The strong interaction of electrons of these groups with each other or with collective electrons of outer shells represent a peculiarity imparting the unique properties to a variety of the compounds containing atoms of transition and rare-earth elements. The investigations carried out over the last fifteen – twenty years have shown that for these compounds the diverse physical phenomena are possible. Among them are phase transitions resulting in the magnet-ordered phases and superconductivity, dielectric and metal states; transitions with appearance and disappearance of the localized magnetic moments. The specified properties are the consequence of strong interactions of electronic and magnetic degrees of freedom. The systems with strong interaction of electrons are referred to as the strong-correlated systems [23] .

Among fundamental processes, the intramolecular rearrangements involving delocalization of unpaired electrons from ligands to metal (e.g., cobalt) ion changing valency of the latter are of special importance. Such rearrangements are commonly referred to as valency tautomerism. Relative to compounds of the first transition group, the specified intramolecular processes lead to the population of metal 3d-tal orbitals with unpaired electrons. The investigations have shown that magnetic properties of compounds can change dramatically in the course of transition of molecules from state A to state B and back. It has been illustrated, in particular, on the example of spin phase transitions in nanosized structures of transition metals using the Co(SQ) 2 (2-2´-dipyridine) complex [24].

A Co¹¹¹ ( SQ )₂ ( 2 - 2 '- dipyridine )

B   Co¹¹ ( SQ )₂ ( 2 - 2 '- dipyridine )

Without discussing the above phase transition in detail, one should bear in mind that the compound, which molecules are in the state A , is diamagnetic, and that in the state B is paramagnetic. For coding the numbers (for example, zero and unit), it is possible to employ two states of a paramagnetic molecule, which can be formed owing to phase separation. Since such states correspond to specific structures of a paramagnetic molecule, they can exist under certain conditions as much as long. Migration of an electron between various states (spin heterogeneity) is the self-organization process meeting a condition, which will provide a constant in time realization of two states with significantly different magnetic properties. Here it is appropriate to recall that conventionally the term “q-bit” (qubit - quantum bit of information) describes quantum system with two probable basic states ( 0 and 1 ). This two-level system allows one to create the corresponding elementary base comprising of logic blocks or gates for performing the logical operations, which should constitute a basis for computations performed by quantum computer. We mean here, first of all, the logic gates "NOT", "OR", "AND". So, two q-bits, each containing unpaired electron, allow logic operation "NOT" to be performed. Other logic operations realized in the computer can be organized in a similar fashion. For this purpose, the devices which would carry out repeatedly the corresponding logical operations should be used as initial universal logic blocks. In other words, these devices (logic gates) should possess the reversibility properties. Among such devices is the Toffoli three-bit gate [see, for example, 6].

• IV.    A Block-diagram of a Quantum Device Based on a Visualized Massif of Q-bit states

  A chart of the device for quantum computation can be represented as follows [25]. We start with the assumption that the main component of the device is a 1 cm² block, where about 10¹⁰ nanotriggers can be placed. Further, each nano-trigger, obtained from grapheme nanoribons, is operated by an element, which represents a quantum dot with two states. Such quantum dot is created on the basis of compounds, which molecules (clusters) are characterized by the intramolecular rearrangement, in particular, valence tautomerism. In general, such system is quantum in essence. Therefore, such element can be used to design the device, which operation is completely defined by the laws of a microworld (quantum physics). The change of the trigger state is a result of quantum dot transition from one state to another. Three nanotriggers are united in a group, which should play a role of the universal gate. Let us further assume that operation of such gate can perform logical operation OR-NOR. It means that the state of one of three q-its (q-bit of the purpose state or computation outcome) changes in only case, when two other q-its (bits of the sources symbolizing the initial information necessary for implementation of the quantum computation procedure)

have strictly concrete value. According to this, the switching between three triggers will make it possible to realize logical operation OR-NOR, i.e. one of nanotriggers should act as q-bit of the purpose state or computation outcome. Taking into account the fact that in the absence of such switching, each trigger can operate independently of two other triggers, the organization of their concerted operation at the current level of electronics development is purely routine task.

In view of the foregoing, the computation procedure can be organized if to assume that the initial state of a group from three nanotriggers is also a result of computation. Thus, the condition of the universal gate reversibility is reached. Accepting the fact that the initial state is also outcome of the computation means that this state corresponds to 1.

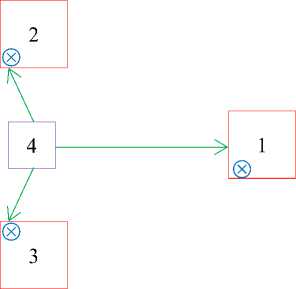
Fig.1. A chart of quantum gate

Violation of such state means zero. Thus, the compotation in a binary system in principle is organized. If to start with the assumption that one square centimeter can contain about 10¹⁰ triggers, then on the specified area one can create about 10⁹ gates participating independently in the procedure of the quantum computation. In reality the number of such gates can be lesser since the organization of the operating electronic device assumes application of other (apart from triggers) elements. Therefore we believe that it is possible to create about 10⁸ gates, which are placed in the block having an area of ten square centimeters. The below figure 1 shows a chart of each of 10⁸ gates. Here 1,2,3 are nanotriggers (possible material for their production is graphene); ⊗ is the quantum dot included in the electronic scheme of the trigger (see above) which, due to self-organization process, transfers triggers from one state to another; 4 is a communication block, which control operation of the triggers, providing, if necessary, coordination of their states. Such block can be made on the basis of the femtosecond laser. The trigger 1 should play a role of q-bit of the purpose stute or computation outcome.

To evaluate the lowest rate of the computation, let us suppose that in each state the quantum dot is for about 10-2 seconds, i.e. long enough. The computation cycle in a binary system assumes realization of two states that takes 2•10-2 s for each of 108 gates. Taking into account independence of their operation, one can conclude the possible device described here should perform 5•109 computation operations per second. It is easy to understand that this value can be considerably increased due to decrease in time of trigger location in each of the states. Further, the calculated unit of the area can be augmented to a square with a size of 10 cm, i.e. to an area of hundred square centimeters. Using these two methods, assuming performance under mild enough conditions, the number of operations can reach 1012 per second, i.e. to one gigaoperations per second. Further processing of information computed in such fashion can be carried out by well-developed software of modern classical computers.

The following should be added to the material proposed in this paper for the nanotrigger (graphene) and control element (quantum dot). Graphene studies have led to the emergence of interest in other two-dimensional materials. It is shown, in particular, that two-dimensional materials on the basis of dihalcogenides of transient metals (DPM) possess various physico-chemical properties. Such materials already have significant prospects of application in a wide range of technologies, in science and technology. In particular, the system graphene/PDM for use in optoelectronics and photonics is promising [26,27]. It is also necessary to note the work conducted under the supervision of professor V.I. Minkin on synthesis and research of paramagnetic complexes of transition metals with various heteroatomic molecules. Materials on the basis of such compounds can be used for the purpose of significant expansion of types of quantum dot intended, as it is suggested in the given work, for maintenance of nanotriggers [28].

• V.    Conclusion

The device described in this work operates using the principles of nanotechnologies and nanomaterials. In this direction, an important point is the justification of the incorporation of rather expensive additional unit into classic modern computers. Such electronic unit is based on a system of nanotriggers, which should be made of two-dimensional material, in particular, graphene. This system correlates with all possible, including entangled, states of a quantum system that provide a large mathematical information resource. The above nanotriggers are employed to create quantum gates, capable of performing logical operations and having reversibility. Each quantum gate contains a quantum dot, which represents a control element that has two essentially different (in magnetic properties) states. In particular, the dot can be formed from materials based on compounds, in which intramolecular processes lead to the population of metal 3d-orbitals due to valence tautomerism. Other compounds with unfilled 3d-, 4f-, and 5f-orbitals, which are characterized by intramolecular rearrangements, can be used to design quantum dots, the controlling elements of a quantum gate. The abovementioned block is intended for quick processing and analyzing a very large array of data. These arrays are needed to solve specific problems of the most diverse branches of science, technology, and other fields of human activity. In this regard, it can be stated that there are many typical problem-solving methods. Knowing the condition of such problems, one can set the number of qubits m, which determines the number of possible states (2m), which ultimately allow obtaining the required data bank. The approach proposed in this paper permits to principally solve the problem of qubit decoherence. Indeed, the nanotriggers and quantum dots are formed under the conditions of controlling their structure and intramolecular dynamics, and therefore can be used as elements of an electronic device for an arbitrarily long time, and the number of qubits in the described device can be increased if necessary.