Quasi-de Sitter solution in F(T, (T )2) teleparallel gravity

In this work, we propose modified teleparallel gravity of F(T, (VT)2) version and investigate cosmological quasi de Sitter solutions within it. Cosmological equations for general version F(T, (VT)2, ПТ) have already been represented in the work of G. Otalora and E. Saridakis [1]. We study simplicated model using the result of [1].

Настоящая работа выполнена в рамках Дополнительного соглашения №073-03-2024-060/1 от 13.02.2024 к Соглашению о предоставлении субсидии из федерального бюджета на финансовое обеспечение выполнения государственного задания на оказание государственных услуг (выполнения работ) № 073-03-2024-060 от 18.01.2024, заключенным между ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» и Министерством просвещения Российской Федерации.

• 1.    Cosmological equations

Modified teleparallel gravity with higher derivatives with respect to the torsion scalar of the form F(T, (VT)2, ПТ) was constructed in [1]. The action of the model has the form： s = 2 /d4，eF (T (VT )2, □?)+ sm(e^, Фт), where T is the torsion scalar, e = "е^е^) = ^-ž tetrad de terminant, (VT )2 = rjAB e；e£ V^T V” T = 严VMTV”T. □T = VMVMT. Фт a general field of matter. A\e consider a truncated version F (T, (VT )2) in the Friedmann- Rob er t son-AValker me trie：

曲2 =近2 - q2⑴心, dxldx^,⑵ which arises from the tetrad e^ = d，@g(1, q(。，q(。，q(。)， where q = q(。is the scale factor.

The dynamic equations for the cosmological model with a perfect fluid [1] for truncated F(T, (VT)2) model are the following:

Ft Я2 + 24H2Fy (3ЯЯ + Я) Я + 24H3 方Fx + —=迎,(3 )

Ғ_ТЯ + "FT + 24Я [2ЯЯ + 3(Я + Я ²)Я]Ғу + 24Я ²ҒуЯ ⑶ + 24Я ²Я—х + 24—хЯ ² (12Я² + Я)+

+24ЯҒх (4Я + 3Я2 )Я = - ^,(4)

where X = (VT)² ： T = -6Я² ： T = 零 =Т2ЯЯ ： X = T² = 144Я ²Я ², Ғ_х = 装. Hereinafter wo omit the index m for density p_m and pressure 9_m ， -

By analogy with investigation of /(—, ( ▽冗 )²) [2] we choose the function Ғ(T, (VT)²) as

Ғ = ATn + ^(T)X, A> 0, A = con^t.(5)

An exponent of torsion scalar n is a natural number.

The derivatives of the function Ғ(T, (VT)2) with respect to T, X and time t are

F_t = AnT " ^-1 + 3_TX, F t = An(n - 1)T " ^-2T + 3_TTTX + 3_TX,

—Х = 3(T), —X = 3tT = 3T, —Х = 3ttT + 3tT.(6,)

Here we are using abbreviated notation 3T = 岩 ,зтт = ^T2 and so on.

Substituting the relations above into equations of cosmological dynamics (3) and (4) we get:

(AnT "^{- 1} + 3_Tx )Я² + 24Я 3з(3ЯЯ + Я) + 24Я ³Я3_T T + ^AT ” + ^3X = 迎,⑺

12              6

(AnT"^-1 + 3 t X)Я + Я(An(n - 1)T"^-2T + 3 tt XT + 3 t X ) + 24Я(2ЯЯ + 3(Я + Я²)Я)3TT+ + 24Я ²Я(з_TTT ² + 3_TT) + 24Я ²Я ⑶ 3 + 24зЯ2(12Я² + Я) + 24Яз(4Я + 3Я ²)Я = - ^9m. (8)

To solve the field equations (7) and (8), it is necessary to choose the values of the Hubble parameter.

In present work, as an example, let us consider the quasi-de Sitter model.

Let us represent quasi-de Sitter model in the following form:

Я = Я* + ee^-B* q = Q0 exp ^Я*t - *e^-B),

⑼

where e 《 1, Я*, В - const. and Я*, В > 0.

In our case, the Hubble parameter contains zero and first order parts with respect to infinitesimal parameter e. Therefore we represent the density and pressure in the same manner： p = Po + ebp, 9 = 90 + eb”

• 2・ Solutions for zeroth and first order perturbations in e

Taking into account quasi-de Sitter model (9) with H = H * + ee^-Bt and its derivatives H = -еВе - Bt, H = eB²e"^Bt, we can derive equations for zeroth and first order perturbations in e. By substituting H( 力 )from (9) into equations (7) - (8), and taking into account ， T = 12H* eBe ~ ^Bt , X = ( 力 )2 = O(e²), T² = O(e) we obtain the equations on the density and pressure up to first order in e:

12AnH2^ⁿ ~ 1 + 36AnH * ee^-Bt£ ⁿ ~ 1 + 2883H3eBe^-Bt(B - 3H*) + Af 〃 = 2(p° + ebp 他 ),     (П)

2AnBee ~ ^Bt^ⁿ - 1 + 4Amm - 1)ee"^Btfⁿ"1 - 483H2B³ee^-Bt - 144H3В²ee^-Bt = po + ebp, (12) where £ = -6H2, £ < 0.

Next, extracting zero-order term from obtained equations we find the following relations for the density po and pressure po of the matter ：

A 口 (1 - 2 九) =2po, po = 0.                              (13)

Note, there is no vacuum solution due to absence of possibility to set po = 0 without setting A = 0. Also, let us mention that for odd 几 we have phantom type model po <  0, or in scalar field representation 2 j²<  -V (0). So if V (0) > 0 kinetic temi should be negative.

Considering the first order of smallness with respect to e from equations (11) and (12), we obtain expressions for the density perturbations bp and pressure bp:

bp = 18AmH*e-Bt£n"1 + 1443H3Be-Bt(B - 3H*),(14)

bp = 2Ane~Bt£n-1 (B + 2九-2) - 48H2B2e-Bt(3B - 3H*).(15)

From equation (15), for the case of zero pressure perturbation bp = 0 we express 3 ：

• 3 = ŽT^ [B + 2(n - 1)] £n-2 + ~ET.

4BB

Then we substitute this expression into the density perturbation equation (14) and obtain the dependence of the density perturbation on time in the absence of pressure perturbation:

bp = e-Bt (12£2(B - 3H*) + AnH*£n-1 19 + 2s J - 3£ - 6(,1)£ ) .(17)

Now we can construct graphs of the dependence the density perturbation on time in the absence of pressure perturbation.

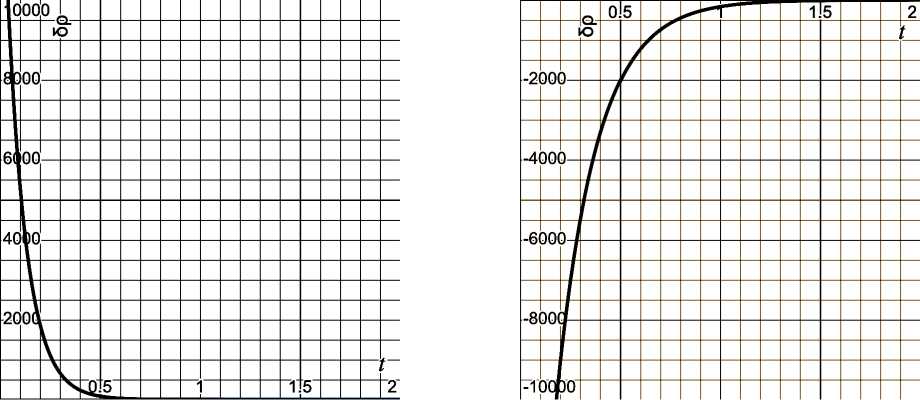
a)                                                    b)

Fig. 1. Graph of the dependence 6p ⑴ for a) odd n values and b) even n values

As we can see, the perturbation of density exponentially decreases over time, which can be clearly observed in the graphs. In both cases, the perturbation of density decreases and always tends towards zero. The construction of these graphs is only possible when n e N, and depending on the parity of its value. The behavior of the perturbation of density will tend from positive or negative values towards zero. Regardless of the parameters introduced for the following positive constants "*,A, and g, their influence on the dependency is insignificant.

Conclusion

Thus, we considered a truncated model of the form F(T, (VT)2) = ATⁿ + ®(T)X and showed that in the presence of cosmic dust (po = 0, 8p = 0) there is a stable quasi-de Sitter solution of the form H = H* + E£^-B*. Pure de Sitter solution (13) is allowed also. Investigated model belongs to the class of eternal inflation.