Рабочие уравнения линейной крутильной вискозиметрии

Вязкость является структурно чувствительной характеристикой веществ, по которой судят, например, об изменениях материала, возникающих во время технологических процессов. Для ее измерения используется ряд приборов, описанных, в частности, в [1]. При высоких температурах / и давлениях круг инструментов сужен и часто применяется крутильный вискозиметр [2]. Математическое описание процессов, протекающих в нем, выполняется на основе общих теорем динамики: об изменении импульса объема жидкости в рамках подхода Эйлера или Лагранжа и об изменении момента импульса тигля, принимаемого абсолютно твердым телом, относительно оси вращения. Традиционно полагается ньютоновский характер жидкости, т.е. линейная зависимость между напряжением ст и скоростью сдвига D, когда ст = 0 при D = 0. Для практических прило жений адекватны точные решения, получаемые при следующих допущениях: скольжение между средой и внутренней поверхностью тигля отсутствует, амплитуды колебаний малы, т.е. течение жидкости в цилиндре осесимметричное и существенной компонентой вектора скорости является азимутальная. При этом переходный режим затухающих колебаний не рассматривается.

Одно из таких решений получено Швидковским Е.Г. [2]. Здесь вязкость v в прямой задаче вискозиметрии определяется из вискозиметрической системы уравнений:

Г,     (         ,  2 >          гп     (      2 ,2 Л

а)~ = Р 1 + ^—^ -2р0,— = q 1-^-^ илиб) L’+L”- = 2K(p-Ро);(1)

к  I p+q)    к  ( р +q )9

Z' = Re(Z), Z" = Im(Z), L = -2vMpMl + 4——У^th^ⁿ

где 3 = RsTkiv , 0„ = Д-klv, k = p + iq, р = 8!т, р0=80/т0, q = 2nlr, i = 'J-i; Jt - функ- ции Бесселя первого рода Z -го порядка; К - момент инерции пустой подвесной системы; L -функция трения; М - масса жидкости в вискозиметре полувысотой Н и радиусом R; р, q - коэффициент затухания и циклическая частота колебаний; 80, т0 - логарифмический декремент затухания 6 и период г колебаний вискозиметра при М = 0; рп - корни уравнения Jx{pnR) = 6. Принято число торцов a = 2: образец смачивает крышку вискозиметра или на его поверхности присутствует пленка.

Выражение (2) представляет одно из точных решений, полученных впоследствии в [3]:

(5 + Д0)2 +l + Z>(5) = 0, 5] 2 =T0(-A + f)/r,                       (3)

где представленные соотношения для D(s) являются математически эквивалентными, преобразуются из одной формы в другую и эффективны в различных ситуациях:

'Js^I^^^ Ло _И=1 P\_ns_p

^Ло Я £₀ ^о[(^{2т + 1}) ^m

,      , “   1 Г th(5„70)

ад = 52^-853лУ^-^- 1--;

Елюхина И.В., Никитин Д.Ю.

Рабочие уравнения линейной крутильной вискозиметрии

Z)(5) = s^zA --— У У -=------X------.

я-²   ^₀р?_п(2т + 1)²(8-_5пт)

В (3), (4) величины

A = MR?!2K, £_Q=R/d, q₀=H!d, d = ^7^,Ь = 5!№, M\_n=M_nR, 4 = Ал/ ^о + ⁵, ^ = ^s + [(^2m + 1>/(2^₀)]² = ^s„m = ~[(^2w + l>/(²7o)f - Ал Ло ;

А - отношение моментов инерции замороженной жидкости в тигле и К; d - толщина пограничного слоя; Н - полувысота образца при a = 2 и высота при а = 1; 7, - модифицированные функции Бесселя I -го порядка.

Выделенные решения (1)—(4) найдены без дополнительных к отмеченным ранее предположениям и их можно рекомендовать для обработки опытных данных. Обзор основных упрощенных зависимостей для расчета вязкости ньютоновских жидкостей выполнен, например, в [4]. Часто на практике используются формулы Швидковского Е.Г. для слабовязкого приближения, которые при низких / из исследуемого диапазона при реализуемых в эксперименте условиях могут приводить к некорректной картине свойств. Вместо традиционного решения методом последовательных приближений [2] здесь можно осуществить минимизацию по v значений функции

Ф<У) =

J_f К У ^5 -т5₀/с₀^ тс V MR J     tct(v)²

—>min,

<т(у) = 1-^ 2g

зы2

8 U

3    ! 27? Л 1                   £_Imf ^R* )

R^tc/^tv) H _n=1 R^Tc/^Tv) | (v²/z²/?²^J q l^v²//²/?²^ )

Сумма ряда в последнем слагаемом обычно заменяется выражением (b-cp/q) [2], где дискретные значения коэффициентов b и с даны в таблице 1 в [2] и могут быть интерполированы на весь интервал, например, кубическими сплайнами. Результаты по вязкости, получаемые из (1а), (2) и (5), тогда совпадают в пределах 0,1 % в рассматриваемой области £₀ > 10, т.е. при вычислениях по такому варианту существенно понижается их трудоемкость без потери точности.

Система (1а), (2) предпочтительна для обратной задачи вискозиметрии. Очевидно, что при использовании и мнимой Im, и действительной Re частей вискозиметрических уравнений минимум некоторой целевой функции /, являющейся критерием соответствия экспериментальных и расчетных данных, на множестве двух параметров т и 5 более выражен (рис. 1а). При расчетах только по Re или Im на оси возникающего, как и на рис. 16, оврага появляются локальные минимумы. В модели (16), (2) не содержится период г0, зависящий от нагрузки на нить и t, т.е. подлежащий измерению во всем рабочем интервале t с опытной нагрузкой на нить, и требуемый при расчете по (1а), в связи с чем модель обладает преимуществом в прямой задаче. Функция качества, построенная по Re от уравнения (1а), (2), более пологая, т.е. влияние ошибок в наблюдаемых параметрах на оценку v выше, а более выраженный минимум Im(/) смещается сильнее вследствие ошибок в т. На рис. 1 отмечены интервалы т'±(т'-т0) и ^Ч^'-^о), где т', б’ отвечает минимуму f(r,S)', расчеты проводились при 7? = 1 см, р = 6 г/см3, г0=5 с, Л = 0,15, 2НIR = 2,5, £0 ~ 11; моделирование закона колебаний тигля выполнено по (1а), (2).

Для линейных жидкостей при наличии упругости характеристики, входящие в реологический закон, также, как и для ньютоновских сред, представляются вне переходных процессов функциями, изменяющимися по закону ехр(-Аг), а вместо ньютоновской динамической вязкости q в уравнения, в частности, (1), (2) вводится комплексная вязкость q* . При заданных допущениях теории метода, например, для модели Олдройда q, ^q^-kX^K^-k^ , где ^ и ^ ~ время релаксации и запаздывания. Для простейших моделей вязкоупругих жидкости и твердого тела, т.е. моделей Максвелла и Фойгта, выражения для вискозиметрических функций отмечены в [5,

Физика

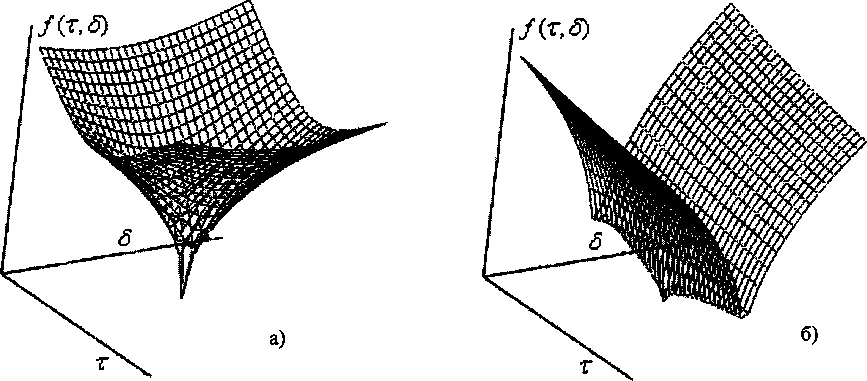
Рис. 1. Поверхность функции качества /(т, 5) при расчетах по моделям (1а), (2) (а) и (16), (2) (6)

• 6] . Пусть имеем последовательное соединение двух элементов: вязкого элемента Ньютона и параллельной комбинации вязкого и упругого элементов Фойгта. Тогда, например, для простого сдвигового течения о^ = T)\D\, ст_г! G₂->r ст₂! 1^ = D₂, где G - модуль сдвига, 1, 2 - номера элементов, точкой обозначена производная по времени. Для такого соединения ст = а_х = сг₂, D = D_X + D₂ , и получаем, что ст = t)_xD-t)_x ^ct/G₂ +<т/т7₂), т.е. щ = ?7₁/[1 + 7₁ (1/7₂ ”^/^2)] • Часто для описания используется модель Бюргера с последовательным соединением моделей Максвелла и Фойгта, т.е. механическая схема которой включает две пружины и два поршня.

Отмеченные особенности представляют интерес при выборе точного решения для аналитических расчетов свойств нелинейных, в общем случае упругих вязкопластичных, жидкостей с различной комбинацией элементарных моделей. Построение и аппаратное приложение подобных решений целесообразно сопроводить детальным анализом их чувствительности [5].

Работа выполнена при поддержке РФФИ (грант № 07-02-96016_урал).