Рациональная конструкция магнитного фиксатора в съёмном зубочелюстном протезе

Актуальность проблемы фиксации и стабилизации съёмных зубочелюстных протезов обуславливает необходимость разработки конструкции магнитного фиксатора, оптимального в смысле простоты использования, биологической совместимости и эстетики [4, 5, 13].

Обзор многочисленных работ [1, 2, 6–12] позволяет сделать вывод о том, что использование замкнутого магнитного контура оправданно не только из-за снижения эффекта размагничивания постоянных магнитов, но и в силу локализации магнитного поля и снижения влияния последнего на живую ткань [8–12].

Учеными Пермского государственного технического университета и Пермской государственной медицинской академии, коллективом авторов (академика В.Н. Анциферова, профессора Г.И. Рогожникова, профессора Ф.И. Кислых, профессора А.И. Цаплина, доцента Н.Б. Асташиной, доцента Г.Н. Вотинова, к.м.н. С.И. Рапекта, к.м.н. С.В. Казакова, к.м.н. А.А. Сметкина) разработано устройство для магнитной фиксации съемных зубочелюстных протезов (полезная модель №74064 от 20.06.2008). Предлагаемое устройство (рис. 1) состоит из зубочелюстного протеза 1 , в базис которого введен самарий-кобальтовый магнитный элемент 2 с магнитопроводом из ферромагнетика 3 и челюстного имплантата 4 , выполненного из углеродного материала «Углекон - М», с зафиксированным в нем ферромагнитным компонентом квадратного сечения 5 , через который магнитная цепь замыкается. Имплантат закрывается тонким

• © Анциферов В.Н., Рогожников Г.И., Вотинов Г.Н., Асташина Н.Б., 2008

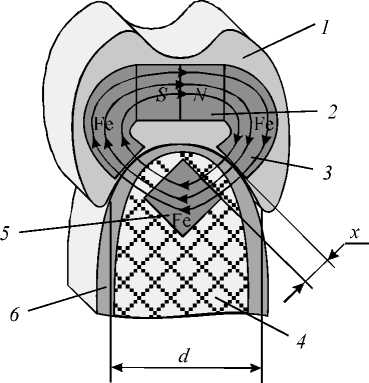
Рис. 1. Модель магнитного фиксатора: 1 – зубочелюстной протез; 2 – самарийкобальтовый магнит; 3 – магнитопровод; 4 – челюстной имплантат; 5 – ферромагнетик; 6 – слизистая оболочка; x – расстояние между ферромагнетиками; d – эффективная ширина области контакта слоем слизистой оболочки 6. Силовое взаимодействие между ферромагнетиками 3 и 5, находящимися на расстоянии x, должно обеспечивать надёжную фиксацию и стабилизацию ортопедической конструкции 1.

Магнитный элемент 2 имеет форму цилиндра и может быть расположен в любой точке магнитопровода 3 , однако близкое размещение к ферромагнетику 5 затруднено из-за нарушения требования комфортности пациента, трудности закрепления и последующей коррекции (например, замены при размагничивании).

Предполагается, что данное устройство позволит надёжно удерживать зубочелюстной протез при различных воздействиях функциональной нагрузки. Обоснованность предположений авторов будет проверена во время проведения экспериментальных и клинико-лабораторных исследований.

Экспериментальное определение силы взаимодействия

ПОСТОЯННОГО МАГНИТА С ФЕРРОМАГНЕТИКОМ

Трудности теоретического прогнозирования силы взаимодействия постоянных магнитов с ферромагнетиками обусловили проведение натурного эксперимента. Лабораторные испытания проведены в лаборатории № 1 Института механики сплошных сред Уральского отделения Российской академии наук на установке 1925 ПА10 М (рис. 2). Эксперимент проводился для двух самарий-кобальтовых магнитов круглого сечения, отличающихся диаметрами сечения. Длина магнитных элементов l = 5 мм; диаметр магнита № 1 d 1 = 5 мм; диаметр магнита № 2 d 2 = 3,5 мм. Объёмы: V 1 = 98 мм³, V 2 = 48 мм³.

Для чистоты эксперимента образцы приклеивались к парамагнитным подложкам (рис. 3), уменьшая влияние окружающих ферромагнетиков.

Сила взаимодействия магнита с ферромагнетиком прямо пропорциональна величине магнитной индукции B 0 вблизи полюсов магнита и имеет некоторую зависимость от расстояния f ( x ), определяемую экспериментально.

Магнитная индукция B 0 вблизи полюсов магнита прямо пропорциональна величине намагниченности J и объёму магнита V :

F ~ B 0 f ( x )~ JV f ( x ).

Рис. 2. Лабораторная установка

а                      б                      в

Рис. 3. Образцы на парамагнитной подложке: а , б – самарий-кобальтовые магниты, диаметры сечений 5 и 3,5 мм соответственно; в – имплантированный ферромагнетик

В случае если исходные самарий-кобальтовые магниты намагничены до насыщения, остаточная намагниченность у них также будет одинаковой (и являться их характеристикой). Таким образом, сила взаимодействия магнита с ферромагнетиком прямо пропорциональна объёму магнита и зависит от расстояния

F ~ Vf ( x ) .

В результате эксперимента по растяжению системы магнит–ферромагнетик самописец установки выдавал непрерывный график зависимости силы их взаимодействия от расстояния (рис. 4). Приборная погрешность 0,01 Н.

Таблица 1

x , мм	0	0,5	1	1,5	2	2,5	3	3,5	4
F ( x ), Н	3,9	2,0	1,08	0,6	0,34	0,2	0,12	0,06	0,04

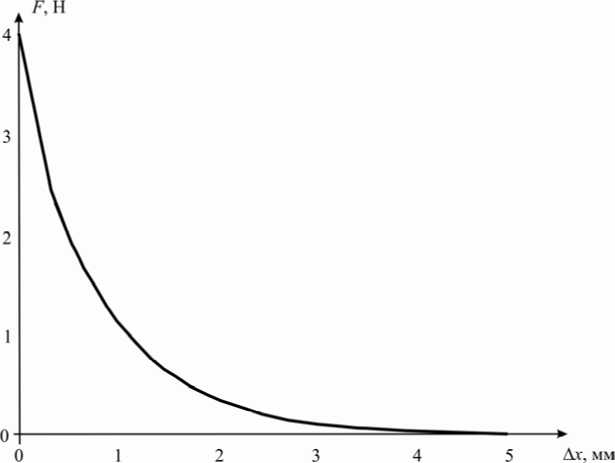
Рис. 4. Экспериментальный график зависимости силы взаимодействия самарийкобальтового магнита с ферромагнетиком от расстояния между ними (магнит № 1)

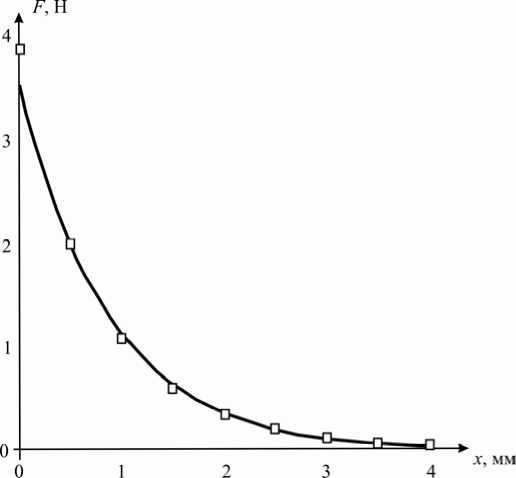
Рис. 5. Аналитический график зависимости (сплошная линия) и экспериментальные точки для магнита № 1

Легко видеть, что данная зависимость имеет экспоненциально убывающий характер и в первом приближении с учетом соотношения (1) аналитически её можно описать функцией вида

F ( x ) = AV e - kx ,

где V – объём образца, A и k – некоторые постоянные коэффициенты.

Для магнита № 1 снятые численные значения зависимости силы взаимодействия от расстояния (для N = 9 значений) приведены в табл. 1.

Коэффициенты A и k определяются с помощью метода наименьших квадратов.

Прологарифмировав соотношение (2), учтя, что V = V1 и введя обозначения y = InF, a = ln(AV1), приходим к линейной зависимости y = a - kx.

Согласно методу наименьших квадратов следующая функция двух переменных должна стремиться к минимуму,

NN

f ⁽ a , ^k ) = E ⁽ У / - y ⁽ x i )) 2 = E ⁽ y i - a + kx i ^{) 2} ^ min .

i=1

Следовательно,

^	'd f   „Nz —=- 2 E ( y i- - a + kx i ) = 0; d a        i = 1 d f« = 2 E ( x i ( yt - a + kxi )) = 0- d k    *=7

Приходим к системе линейных алгебраических уравнений

NN aN - k £ Xi^ y/;

I=1

NNN a E x-k E xi-2=E xiyi,

^    i=1              i=1

решив которую, находим a = 1,264 = ln(AV1); k = 1,144; A = exp(a)/V1 = 0,0361.

Получаем аналитическую зависимость силы взаимодействия используемого постоянного магнита с ферромагнетиком как функцию расстояния между ними,

F ( x) = 0,0361 V e -1^y44 x ,                                      (3)

где сила F измеряется в Ньютонах, объём V – в мм³, расстояние x – в мм.

График данной зависимости с нанесёнными экспериментальными точками (см. табл. 1) для магнита № 1 ( V 1 = 98 мм³) приведён на рис. 5, откуда видно совпадение численных значений силы в практически интересующем диапазоне расстояний (от 1 мм до 4 мм).

Соотношение (3) даёт удовлетворительное соответствие с экспериментальными данными и для магнита № 2 ( V 2 = 48 мм³).

Таким образом, силу взаимодействия произвольного самарий-кобальтового магнита с ферромагнетиком можно оценить с помощью аналитической зависимости

• (3). Уникальность данного соотношения состоит в том, что оно справедливо для самарий-кобальтового магнита цилиндрической формы произвольного объёма V , причём сечение магнита может быть как круглым, так и овальным, квадратным и др., что немаловажно при учёте особенностей пациентов.

Расчет параметров магнитного фиксатора

• 1.    Исходные данные для расчёта рациональных параметров базовой модели

Комфортная сила удержания протеза (результирующая сила) F рез составляет около 1,2 Н [3]. В расчёте на 12 см длины l протеза челюсти вдоль зубного ряда получаемое значение силы на единицу длины F_l составляет около 10 Н/м. В дальнейшем цифры могут быть уточнены (с учётом клинической ситуации).

Ширина области контакта протеза d составляет порядка 1 см (см. рис. 1).

Давление p (нормальное напряжение с ), оказываемое протезом при нормальном удержании,

F F, .

p = с = —= -= = 103 Па, ld d что является минимальным давлением, оказываемым протезом на живую ткань.

Относительную деформацию живой ткани а можно оценить с использованием закона Гука с = E а, где E – модуль Юнга (для мягких околочелюстных тканей E = 0,5 МН/м2 [7]), а = с / E = 2-10-3.

Ах а = —, x где x – расстояние между ферромагнетиками (см. рис. 1). При x = 2 мм абсолютная деформация Ах составляет 4-10-6 м, что можно считать незначительным (пренебречь).

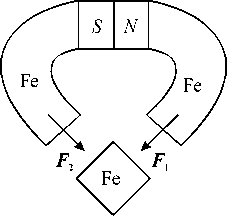
Рис. 6. Магнитный контур

F

Рис. 7. F – сила, действующая на протез в расчёте на каждый магнитный контур

где k – количество замкнутых магнитных контуров, приходящееся на протез. Таким образом,

F pe3 = V2 kF o .

F Н

Учитывая, что —— = Fl = 10 , можно рассчитать количество контуров на lм единицу длины.

2 kF 0

F=—г ■ откуда

Fl к = —р=— .

2 F 0

Поскольку F_l задаётся из условий комфортности пациента, то количество контуров на единицу длины зависит практически только от силы F 0 взаимодействия ферромагнетиков, которая, в свою очередь, зависит от расстояния x между ними. На практике значения параметра x изменяется в пределах от 2 до 3 мм.

Результаты расчёта эффективного количества контуров k при l = 5 см длины протеза приведены в табл. 2.

Приведённые в таблице значения количества контуров (при l = 5 см) рассчитаны для самарий-кобальтового магнита объёмом V 1 = 98 мм³.

При необходимости может быть решена и обратная задача. Задаётся количество контуров k на длине l и эффективное расстояние между ферромагнетиками x . По формуле (4) находится значение F 0 .

Fll

F 0 = 2к к'

Далее по полученному соотношению для силы (3) находим необходимый объём магнитного элемента

V = ------ F ⁰ 1144 .

0,0361 e ^{- 1}’¹⁴⁴ "

При практической реализации данный объем может быть разделён между двумя магнитами, включенными последовательно в магнитную цепь, показанную на рис. 6.

Таблица 2

x , мм	2	2,5	3
F 0 , Н	0,34	0,2	0,12
k	« 1	» 2	« 3

Выводы

• 1.    Предложена рациональная конструкция магнитного фиксатора в съёмном зубочелюстном протезе, использующая замкнутый магнитный контур. Решены прямая и обратная задачи оптимизации количества магнитных контуров на единицу длины.

• 2.    Получена универсальная аналитическая зависимость силы взаимодействия самарий-кобальтового магнита (цилиндрической формы произвольного объёма) с ферромагнетиком.

Благодарности

Публикуется при финансовой поддержке гранта Российского гуманитарного научного фонда «Разработка программы комплексной стоматологической реабилитации больных с дефектами челюстей в различных регионах Пермского края».