Рациональный выбор конечно-элементных моделей для модального анализа на примере конструкции сварного металлического каркаса

В настоящее время все чаще при создании динамически нагруженных конструкций как на этапе проектирования и разработки, так и при изготовлении опытных образцов проводят расчет собственных частот и форм конструкций [1]. Это необходимо для того, чтобы в случае близости одной из собственных частот к рабочей внести требуемые конструктивные изменения и избежать резонанса. Еще один вариант применения модального анализа – проверка динамического поведения конструкции при появлении в ней различных дефектов [2] (дефекты приводят к сдвигу собственных частот, появлению дополнительных форм колебаний, что позволяет их идентифицировать).

На сегодняшний день программные пакеты, реализующие метод конечных элементов (МКЭ), позволяют проводить модальный анализ достаточно больших конструкций сложной формы, не прибегая к помощи распределенных вычислений. В этом случае выбор рационального типа элементов («Shell», «Solid», «Beam») позволяет значительно сократить время расчета.

Несмотря на очевидные преимущества конечно-элементных методик модального анализа конструкций, они требуют упрощения расчетных моделей, в частности, использования контактных алгоритмов в местах сварных соединений. Габаритные сварные металлоконструкции могут иметь несколько видов сварных швов в своем составе, в частности, иметь пунктирные сварные швы, точное моделирование которых существенно затрудняет процесс расчета.

В данной работе на примере расчета подсборки каркаса нижней части крыши трамвайного вагона 71-631 производства Усть-Катавского вагоностроительного завода проведено сравнение эффективности применения Shell- и Solid-элементов для расчета собственных частот сварных металлоконструкций, методы моделирования пунктирных сварных швов, позволяющие существенно упростить расчетные модели, без потерь в точности результатов.

Расчетные модели

В рамках проекта «Создание высокотехнологичного производства модельного ряда энергосберегающих низкопольных трамвайных вагонов модульной конструкции» потребовалось проведение расчета собственных частот и форм колебаний крыши каркаса модуля средней секции трамвая 71-631 (рис. 1, а ). Конструкция содержала около 150 элементов и несколько сотен сварных швов различной протяженности. Для выбора рациональной расчетной модели в пакете AN-SYS Workbench 14.5.1, реализующем МКЭ, были сделаны 2 расчета подсборки крыши (рис. 2, б ):

б ): с использованием твердотельных элементов типа SOLID186 и оболочечных элементов SHELL63.

Достоинством твердотельных элементов является отсутствие необходимости модификации 3D-модели. Для использования оболочечных элементов было необходимо либо изначально создавать модель, выполненную поверхностями, либо с помощью модуля ANSYS DesignModeler преобразовать исходную 3D-модель в срединные поверхности с дальнейшей доработкой. При импортировании в ANSYS для оболочечной модели также необходимо задание толщин всех деталей.

В обоих случаях конструкция принималась свободно подвешенной, дополнительных закреплений не задавалось. Для моделирования сварных швов в пакете ANSYS Workbench использовались контакты между элементами конструкции типа «Bonded» (склейка), запрещающие любые взаимные перемещения в месте контакта.

В твердотельной модели по толщине профиля задавалось по два конечных элемента для учета влияния изгибающих моментов.

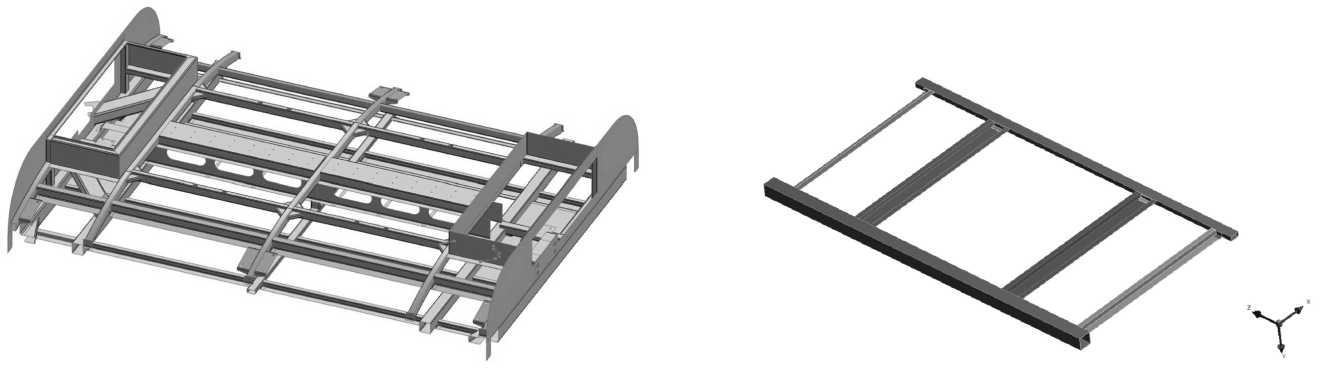
а)                                                                            б)

Рис. 1. а) Крыша каркаса модуля средней секции трамвайного вагона 71-631; б) Подсборка крыши каркаса модуля средней секции трамвайного вагона 71-631

Результаты расчетов

В результате расчета определялись все собственные частоты конструкции в диапазоне от 0 до 50 Гц (табл. 1). Первые шесть нулевых частот, соответствующих перемещениям и поворотам конструкции как жесткого целого, в табл. 1 не приводятся.

Таблица 1

Собственные частоты конструкции, полученные на твердотельной и оболочечной модели

№	Собственная частота, полученная на твердотельной модели, Гц	Собственная частота, полученная на оболочечной модели, Гц
1	6,5	3,5
2	32,6	24,1
3	49,0	26,7
4	–	31,2
5	–	45,1
6	–	47,8

Из табл. 1 видно, что даже на такой несложной модели твердотельные элементы не позволяют определить все собственные частоты и формы конструкции в заданном диапазоне. Оболочечная модель позволила определить помимо найденных твердотельной моделью частот (1, 4, 6) еще три дополнительных. Кроме того, твердотельная модель значительно проигрывает оболочечной как по количеству конечных элементов, так и по времени расчета (табл. 2).

Таблица 2

Сравнение ресурсоемкости твердотельной и оболочечной моделей

Параметр	Твердотельная модель	Оболочечная модель
Количество конечных элементов	382436	201386
Количество узлов	2146160	202722
Время решения, с	2172	74

Для получения более адекватных результатов с применением твердотельных элементов необходимо увеличивать их количество по толщине профиля до 6–8, что исключает возможность использования обычной рабочей станции для подобных расчетов даже таких простых конструк-

Сапожников С.Б., Кудрявцев О.А., Рациональный выбор конечно-элементных моделей Шакиров А.А. для модального анализа на примере конструкции … ций. Расчет собственных частот и форм колебаний всей конструкции крыши, проведенный с использованием оболочечной модели, показал хорошее соответствие с экспериментальными данными, полученными в ходе испытаний на заводе-изготовителе.

Моделирование сварных швов при модальном анализе

Рассматриваемая конструкция крыши трамвайного вагона содержала несколько прерывистых сварных швов значительной протяженности. Точное моделирование таких швов требует трудоемкого изменения геометрических параметров конструкции (создание новых линий или поверхностей). Поэтому актуальным является расчетное исследование влияния конфигурации сварного шва на собственные частоты сварной конструкции. В качестве представительной конструкции при расчетном исследовании рассматривались пластина и профиль толщиной 6 мм, соединенные между собой по грани профиля пунктирным сварочным швом (рис. 2).

Были рассмотрены три варианта моделирования пунктирного сварного шва: простая склейка по линии контакта, склейка по пунктирной линии, повторяющей прерывистый шов, создание промежуточной поверхности (ширина 0,8 мм) меньшей толщины между профилем и пластиной. Утонение переходной поверхности в два раза до 3 мм должно было моделировать предполагае-

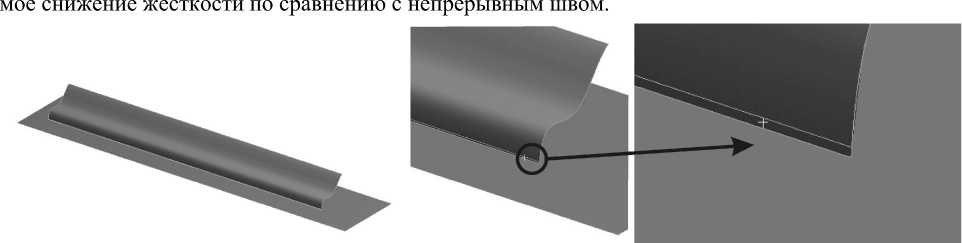
а)

б)

Рис. 2. а ) Модель, рассматриваемая в тестовом примере б ) Переходная поверхность для моделирования возможного понижения жесткости пунктирного сварного шва

Считалось, что в пунктирном шве протяженность сварки составляла половину от всей длины линии контакта (соотношение общей длины проваренных и непроваренных отрезков составляло 1/1).

Модальный анализ показал, что влияние конфигурации контакта наблюдается только на собственные частоты колебаний выше 150 Гц (табл. 3). Следует отметить, что рассматривался неблагоприятный случай: единственный сварной шов, оказывающий значительное влияние на жесткость, малое количество отрезков со сваркой и без нее и их большая протяженность (по 90 мм).

Повышение частоты мест сварки, как в реальных конструкциях, будет приводить к повышению частоты, на которой становится заметным влияние способа моделирования пунктирного шва. Для большинства конструкций транспортных средств наибольший интерес представляют частоты до 150 Гц, поэтому непосредственное моделирование пунктирных сварных швов прерывистыми линиями было нецелесообразно, контакт задавался аналогично с непрерывным швом. Данный результат позволяет существенно снизить время на подготовку расчетных моделей для модального анализа. При анализе прочности конструкции такой подход недопустим.

Таблица 3

Сравнение величин первых десяти собственных частот тестовой модели при разных подходах к заданию сварного шва

№	Частота колебаний, Гц
	При задании контакта по пунктирной линии	При задании контакта по линии	При использовании переходной поверхности меньшей жесткости
1	66,10	66,28	66,08
2	98,35	98,89	98,28
3	150,94	152,40	151,37
4	186,84	198,00	183,90
5	203,86	208,06	203,07

Выводы

При проведении модального анализа сложных конструкций более эффективными являются оболочечные модели, несмотря на необходимость доработки геометрической модели конструкции. В интервале частот, представляющих наибольший интерес для кузовов железнодорожных транспортных средств (до 150 Гц), пунктирные сварные швы могут моделироваться как сплошные без существенных потерь в точности расчетов.