Радиационное давление на неоднородное включение в поле бегущей плоской волны на бесконечной струне

Радиационным давлением на неоднородных включениях на струне давно занимаются ученые и прикладники. Изначально исследованной неоднородностью было колечко, скользящее по струне. Впервые радиационным давлением на колечко, как это часто бывало, заинтересовался Рэлей [1]. Из следующих ранних работ упомянем работы [2, 3] и другие. Из достаточно современных публикаций отметим работу [4].

Однако расчет радиационного давления на струне на неоднородное включение общего вида, насколько известно автору, в достаточно общей постановке изучено не было. Рассмотрение этого вопроса представляет самостоятельный научный и практический интерес. Ранее в работах [5–7] рассматривалось радиационное давление плоской бегущей волны на плоских границах в трехмерном акустическом случае, который в силу геометрии сводился к одномерной задаче, похожей по формализму на случай со струной. В работе [8] в сводящейся к одномерной акустической задаче была решена проблема о радиационном давлении на произвольном включении.

Представляется необходимым, учитывая особенности формализма колебания струны, решить задачу о радиационном давлении конкретно в терминах теории колебания струн.

ПОСТАНОВКА ПРОБЛЕМЫ

Пусть бесконечная струна состоит из двух однородных полубесконечных отрезков: первый x е (-да, -L] характеризуется скоростью звука с1 и плотностью р1 и второй x е[L, да) — c2 и р2 соответственно. Между ними находится неоднородный участок струны x е[-L,L] с переменной плотностью и скоростью звука. Учитывая, что скорость распространения волн по струне, плотность и натяжение струны T связаны соотноше-

T ( x )

нием c¹ ( x ) =----, то указанные распределения

ρ ( x )

можно представить следующим образом:

	c 1 = const,	x < - L ,
c ( x ) = <	c ( x ),	x е [ - L , L ],
	c 2 = const,	x >  L ;
	P 1 = const,	x < - L ,
P ( x ) =	ρ ( x ),	x е [ - L , L ],                (1)
	p 2 = const,	x >  L ;
	T = const,	x <  - L ,
T ( x ) = <	T ( x ),	x е [ - L , L ],
	T 2 = const,	x >  L .

Уравнение малых (с точностью до величин первого порядка малости) колебаний струны с параметрами (1) описывается следующим уравнением [9, с. 128, 129]:

Р ( x ) u ,Af T ( x )^d- ) . (2) d t ² d x ( d x )

Здесь u ( x , t ) — функция поперечных смещений струны относительно состояния равновесия. В случае гармонических колебаний струны и ( x , t ) = U ( x ) e - ^{i m t} из (2) получаем для амплитуды поперечных колебаний

8 (   8lA

-I t ( x ) — 1+ p ( x > ² u = 0,           (3)

dx V     оx J или в развернутом виде

TU "+ T ' U ' + p ( x ) to ² U = 0.

Учитывая, что T ^ 0, последнее выражение перепишется в виде

U "+ ^T ^( x ) U '+ ^P ( x ) to ²U =

T ( x )      T ( x )

= u ₄ IM u '+ ^2— u = o.

T ( x )       c ² ( x )

(3а)

Известно [10, с. 276], что уравнения вида (3а) заменой

- 1 x^p ( '

U ( x ) = v ( x ) e b

(где b — некоторая точка на прямой) сводятся к уравнению v"+ J (x) v = 0,(4)

где

J (x) = q(x) - IMx) — 1 p2( x).(5)

2 dx4

Здесь

ω ²                  T '( x )

q(x) = 47T,     p(x) =      .

c2 (x)

После соответствующих подстановок имеем

U (x) = v (x) T 1/2( x).(7)

Далее будем исходить из наиболее правдоподобного рассуждения о том, что T ' = 0 , что означает постоянство натяжения струны T = const. Тогда уравнение (3а) приводится к каноническому виду (4)

U "+---- U = 0.

c ² ( x )

Из выражения (8) видно, что при непрерывной функции c(x) решение U остается дважды непрерывнодифференцируемой функцией, а при наличии у функции c(x) разрывов первого рода нулевая и первая производные функции U остаются непрерывными функциями, а вторая производная U '' также имеет разрыв первого рода. Отметим также, что в работе [11] приводится достаточно много решений задачи (8), (1) для различных распределений параметров (1).

Задачу рассеяния ставим таким образом: из x = -да ( и -задача) или из x = да ( v -задача) падает плоская волна, которая отражается и преломляется на неоднородности. Введем обозначения k j = to I c j , j = 1,2 и будем рассматривать две подзадачи для уравнения (8), когда асимптотика решения U описывается при | x | >  L одной из следующих комбинаций функций.

• i.    В первой: слева из x = -да набегает исходная плоская волна смещения e ^{ik 1 x} , вызывающая на границе x = - L отраженную волну V i e ^{- ik} 1 ^x , а в полупространстве x >  L преломленную волну W 1 e ^{ik 2 x} .

• ii.    Во второй: справа из x = да набегает исходная плоская волна e ^- i^{k 2 x} , вызывающая на границе x = L отраженную волну V 2 e ^{ik 2 x} , а в полупространстве x < - L преломленную волну W 2 e ^{- ik 2 x} .

V_j , W j — коэффициенты отражения и прозрачности для функций и ( x ), v ( x ), j = 1,2.

Необходимо найти средние силы, вызванные этими полями, действующие на границы x = - L и x = L .

РЕШЕНИЕ ПРОБЛЕМЫ

Согласно пунктам i и ii, имеется два асимптотических решения для функции поперечного смещения струны:

и ( x ) ~		e k x + v e - ik i x We ik 2 x ,	x <  - L , x >  L ;
v ( x ) ~	1	e - ik 2 x + V e ik 2 x ,W2 e - ik i x ,	x >  L , x < - L .

Определим матрицу рассеяния задач i и ii, записанных в виде (9)

5 = f W ¹ V ¹ .

V V 2 W 2 J

Согласно работе [11, с. 111], справедливы следующие соотношения:

k ₂ W i = k ; W 2 ,                  (10)

W2

k2 V 2 =- k -^,

W 1

(1 — |V1|2 ) = k W if,(12)

k ₁

(1 — ^ 2|2 )= T W2Г k2

Отметим, что в выражениях (9)–(13), фигурируют коэффициенты отражения V j и преломления W j , j = 1,2, по смещению U . Черта сверху означает усреднение по периоду колебаний. Поскольку энергетическими характеристиками процесса колебания являются возникающие в струне поперечные силы и скорости, связанные вне | х | <  L через соответствующие импедансы однородных полупространств Z j — р j c j , j = 1,2 [12, с. 127, 128], то целесообразно получить выражения вида (9)–(13) в терминах коэффициентов отражения и прозрачности, например, по поперечным силам.

Предварительно дадим краткую сводку энергетических характеристик гармонического колебания струны [12, с. 125–127]. Поперечная сила и т д и скорость в точке х равны соответственно —T — дх ди и . Например, для бегущей вправо волны eik1,2x д t отношение этих величин равно д и ди и _f c р1, х < — L,

—т — — = I дх/ д t   [ c2 р2, х > L,

		( e ik 1 х — V 1 e — ik 1 х	) ,	х <— L ,
F ~ u	— Tik 1 .	2 W 1 e ik 2 x k 1		х >  L ;
			" ) ,		(14)
		( e — ik 2 х — v 2 e ik		х >  L ,
F ~ v	— Tik 2	k L W 2 e - ik ^, 2 Л-2		х < — L .

Представим (14) в стандартном виде (9) через коэффициенты отражения и прозрачности по по перечной силе Vj, Wj, j —1,2 :

F u

F v

а для бегущей влево волны e ik^12х :

д и Н и и _ I c ^р 1 , ^х < ^— L , ■ т — — — — *

д х/ д t     [ c ₂ р ₂, х >  L .

Получим далее из (9) выражения для поперечной силы:

т ди т--	— т	ik 1 ( e ik 1 х — V 1 e ik 1 х ) ,	х < — L ,
д х		_ ik 2 W 1 e ik 2 х ,	х >  L ;
т д v т--	— т *	— ik 2 ( e — ik 2 х — V 2 e ‘k 2 х ) ,	х >  L ,
д х		- ik ; W 2 e — ‘k ' х ,	х < — L

Или, приводя к стандартному в теории рассеяния виду, получаем

~ — Tik 1 *

'( c iv + V 1 e ^{— х} ) , We ik ^{2 х} ,

х < — L , х >  L ;

~

—Tik 2 *

'( e ^— i^k 2 ^х

+ V , eik 2 ^х ) ,

W 2 e ^— i^k 1 ^х ,

х >  L ,

х < — L.

Сравнивая (14) и (15), получаем следующие выражения для коэффициентов V_j и W_j :

v =-V V =-V v 1 v 1 , v 2 r 2 ,

W 1 — k ² W , W 2 — k L W 2 ;

k ₁               k ₂

k 1 W 1 — k ₂ W , ,

k 1 V ₂ — — k ₂

V 1 W 2 W 1 ,

(1—VI’)—2 Wr.

( 1—№ ) — k ² WI

Отметим, что соотношения (10)–(13) получены для функции U — решения уравнения (8) с асимптотиками (9), исходя из свойств вронскиана реше- д и ний уравнения (8). Поперечная сила —T— д х с асимптотиками (14), (15), вообще говоря, уравнению (8) не подчиняется. Действительно, представим уравнение (8) в виде

LU — ( D ² + a ( х ) ) U — 0,

a ( х ) —

ω ²

c ² ( x )

D ⁿ

d ⁿ d x ⁿ

Воздействуем оператором L на функцию

DU = DU = — dx

LDU = D 3 U + a ( x ) DU .

Учитывая что D ( a ( x)U ) = a ( x ) DU + UDa ( x ), получаем в последнем выражении:

LDU = D 3 U + a ( x ) DU =

= D 3 U + D ( a ( x )U ) - UDa ( x ) =

= D ( D ²U + a ( x )U ) - UDa ( x ) = - UDa ( x ).

Величина LDU = - UDa ( x ) в общем случае тождественно равна нулю только при условии a ( x ) = const.

Тем не менее, например, фундаментальные энергетические соотношения на асимптотических участках (19), (20) точно соответствуют аналогичным соотношениям (12), (13). А именно, учитывая из (16), что | К_у | = |^ ; |, j = 1,2, равны соответствующие левые части соотношений (12), (13) и (19), (20). Вследствие соотношений (16) равны и их правые части. То же справедливо и для соотношений (10), (11) и (17), (18).

Далее рассмотрим энергетические характеристики на однородных участках струны вне отрезка |x | <  L , т. к. именно от них будет зависеть радиационное давление.

Общая энергия струны состоит из суммы кинетической W_k и потенциальной W_p энергий и равна [12, с. 126]

W ( a , b ) = W k ( a , b ) + W p ( a , b ) =

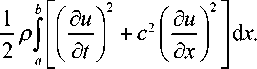
Скорость изменения энергии части струны, лежащей между a и b , получается дифференцированием W(a, b) по времени dW(a,b) dt

—

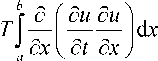
д u д u д t д x

T Г д u д u ( д t д x

~          дu д u_

Величина -T--есть поток энергии в положи-д t дx тельном направлении оси x через точку x [12, с. 127]. Плотность энергии получаем, рассматривая суммарную энергию (21) на единице длины струны:

E = - р

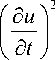
+ c С'

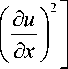
Плотности кинетической и потенциальной энергий в плоской волне совпадают, и суммарная плотность энергии равна

( д u )       [ д u )

E = Pl — I = TI I .              (23)

( д t )     ( дx J

Из (23), а также из равенства -T— / — = рс дx д t непосредственно получаем, что поток энергии плоской волны на однородном участке струны, так же как и в трехмерном акустическом случае, выражается через плотность энергии [5, 8]

т д u д u     ( д u |     „

-T--= рс I     | = сЕ .

дx д t      I д t J

При отражении и преломлении волн без потерь, как и в трехмерном случае [5, с. 359, 364], должен сохраняться баланс среднего потока энергии. В случае отражения и преломления плоских волн силы Fu из (15) такой баланс имеет вид с1 Е 1 = с1 Е', + с 2 Е 2.                    (25)

Здесь черта све р ху о з начае т усреднение по периоду колебаний; E ₁ , E '₁ и E ₂ — средняя плотность энергии в падающей, отраженной и преломленной волнах соответственно. При первичной падающей плоской волне F e ^{ik 1 x} в асимптотике F 0 u в (15) имеем из (23)

^Е - = ^ T I ^ o|^,. ^Е' - = ^ T l ^ «r 1 ^ 12-

^Е 2 = ^ TF ol² W I².

Напомним, что ранее было принято T = const. Подставляя (26) в (25), получаем энергетическое соотношение (19). Соотношение (20) для волн F_v -типа получается аналогично.

(См. Замечание*)).

Перейдем к расчету радиационного давления на неоднородное включение на струне. Это включение вызывает возникновение рассеянной волны. Взаимодействие первичной и рассеянной волн приводит к средней в единицу времени потере импульса, что описывается возникновением средних сил, действующих на включение. Тогда, очевидно, радиационное давление волны на неоднородное включение будет равно разности средних продольных сил, с которыми струна извне действует на оконечности этого отрезка x = ± L .

Продольная сила F - , с которой струна воздействует на границу x = - L , равна

F - =- T cos а - .              (27)

Аналогично продольная сила F + на границе x = L равна

F ₊ = T cos а ₊ .                 (28)

Результирующая сила равна

G = F + + F - .

Здесь a ± — угол наклона струны в точке x = ± L .

Учитывая, что

после разложения до величин второго порядка малости получаем

cos α

1 fd u Y

2 (dx J

Тогда радиационное давление равно

F = F - + F + = ¹ T

G

d u d x

- L

Gu

₍ d x

\

cos а =

V1 + tg² a

*)

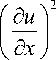
Замечание . Иногда удобнее оперировать плотностью энергии в терминах амплитуды смещения u ₀ падающей волны, отличной от единицы в выражении (9):

u ( x )

^{v (} x ) ~ u 0

Согласно (23), имеем

^F = ¹ ( E l - L - ^E|l ) ,

где E , E — средние плотности энергии на границах x = -L и x = L соответственно со стороны однородных полупространств. Как известно [13, с. 111], для плоских волн, бегущих навстречу друг другу, плотности энергии складываются, не образуя корреляционной добавки, как это имеет место в случае бегущих в одном направлении двух плоских волн. Поэтому имеем, учитывая (26):

E _t= E ,+ F= ^ F ol ¹ + ^F ol ² V I², ^{1 L}                  2T          2T

E L = ^E 2 = ^ T| F o|² W |².

Тогда окончательно имеем для средней силы (29):

e k x + v 1 _e - ik x

W 1 e* 2 x ,

-ik-,x , T7    ik-,x e 2 + V 2 e 2 ,

W 2 e - ^ik 1 ^x ,

x <  - L , x >  L ;

x >  L , x < - L .

(9б)

Умножение выражений (9), (9а) и (14) на величину u ₀

позволяет записать

F = iu о T j    |F ,|² = | u о Tk^ , j = 1,2

для волны F u ( j = 1 ) и F_v ( j = 2 ). Тогда выражения

(26) для F_u -случая перепишутся в терминах амплитуды

смещения u ₀ так:

E 1 = ¹ TU o k J², E \ = ¹ T\u o k J2 V 1J , 2                 2                    (26а)

e 2 = 2 t\u okJ2 WiJ, что уже соответствует принятым в [4] обозначениям.

^F = 2 ( E l - L - E L ) = 2 ( ^E ' ⁺ E '^{- E} 2 ) =

= F T ( 1 + И - W ) .               (30)

Такой результат очень похож на представленный в работах [5, 6] для случая среднего давления на плоскую границу между двумя однородными трехмерными полупространствами, а также на результат работы [8], где рассматривается трехмерная акустическая задача, сводящаяся к одномерной, эквивалентной рассмотренной в настоящей работе. Однако в упомянутых работах среднее давление оказывалось равным (в эквивалентных обозначениях)

F =( El - L - EL )=(E'+ E' 1- E 2 ) , т. е. без понижающего коэффициента 1 / 2 .

Далее приведем пример того, что полученное для радиационного давления на струне выражение (30) работает не всегда.

Контрпример

Воспользуемся приведенными выражениями для расчета радиационного давление на колечко [4]. Согласно этой работе, радиационное давление на расположенное в точке x = 0 колечко при падении плоской волны слева направо равно

F = 2 E 1

z ²

4 + z ²

.

Здесь

m ω ²

z =---- kT

E , = 2 TU о k\²

— средняя плот-

ность энергии падающей волны; m — масса колечка; k = k 1 = k ₂ = to / c .

Попытаемся получить этот результат в рамках полученной теории. Как будет показано ниже, выражение для u -волны (9б) в случае колечка имеет вид ( e - ^{i to t} опущено)

U ( x ) ~ u ₀ <

e ikx

—

+ V 1 e - ikx

•—

W 1 e ikx ,

x <  0;

x >  0;

ikx—-ikx ee

2 ikT

2 ikT )

x <  0;

x >  0.

— Ф ~ Ф

Здесь V 1 =-- , W 1 = 1--— коэффициен-

2ikT          2ikT ты отражения и преломления соответственно по смещению; Ф — поперечная сила, с которой колечко действует на струну, которая равна [4] 2mω2u

Ф =------- ⁰— . В терминах поперечной силы

+ mto2 / ikT выражение (31) преобразуется к виду

Г e ikx + v — ikx , x <  0, F ( x ) ~ F\w «Х1

[ We ikx ,        x >  0,

Ф          Ф

V =---- , W = 1--,

¹    2 ikT        ¹       2 ikT

где F₀ = iu ₀ Tk .

Далее после подстановки (32) в выражение для радиационного давления (30) получаем

F=IT (1+V^ - Wr )=

=TU 0 k f, J»L -1 jyL). 0

4 ^ |2 kT I’      |2 kT |¹ J

Таким образом, применение описанного метода приводит к неверному результату — радиационное давление на колечко оказывается равным ну- лю. Произошло это по следующей причине. При обосновании результата (30) мы исходили из того, что является справедливым однородное уравнение (8). Однако хорошо известно, что в случае с массивным колечком речь идет о приложении сосредоточенной силы, что отвечает непрерывности смещения и разрыв первого рода для ее пространственной производной в точке приложения силы [14, с. 155], что в свою очередь эквивалентно превращению уравнения (8) в неоднородное уравнение с дельтаобразным источником в правой части

Ф

U "+ k ² U = - u ₀ — 5 ( x ),             (8а)

из которого непосредственно и следует решение (31).

Приведенный пример еще раз показывает, что предложенным подходом следует пользоваться аккуратно, учитывая возможность неоднородности уравнения (8). А именно, изложенный подход справедлив, если решение уравнения (8) и его первая производная непрерывны, а вторая производная может иметь разрыв первого рода.

ВЫВОДЫ

В работе был рассмотрен вопрос расчета радиационного давления на неоднородное включение на струне в поле бегущей волны. Как и в акустическом случае [8], это давление выражается через плотности энергии на границах включения, однако с тем отличием, что оно равно не разности, а полуразности средней плотности энергии перед включением и средней плотности энергии за ним. Показано, что полученные соотношения верны при определенной гладкости решения задачи о смещении струны и его первых двух производных.

По аналогии с квантовой механикой приведены свойства элементов матрицы рассеяния получившейся одномерной задачи в терминах коэффициентов отражения и преломления по поперечной силе. Проанализирован физический смысл соотношений между элементами матрицы рассеяния.

Результаты могут иметь существенное прикладное значение.