Random Connection Based Scale-free Networks

Published Online May 2013 in MECS

Recently, researches concerning complex network is uprising. Real systems can be abstracted into networks when we consider internal components as vertices and the relationships among them as edges. Networks exhibit periods of growth, synchronous, coupling, analysis emergence and intervention, expressed as changes to their structure (i.e. topology) and use (i.e. the magnitude of interaction or flow between pairs of nodes) [1]. Therefore, a study on a specific system can be simplified into the study of its corresponding network [2] [3]. According to different contents represented by vertices and different situations showed by edges in different real complex systems, scientists have studied many networks, such as biological networks [4][5], social networks [6][7], information networks [8][9][10], transport networks [11][12]and economic networks [13], etc. Among these studies, complex networks showed two well-known features which have drawn scholars’ interest -the small-world phenomenon and the scale-free powerlaw distribution [14][15]. Besides, researches of complex networks are also well combined with other disciplines, for instance control theory [16][17][18][19], game theory [20] [21], behavior science [22], stock market [23]and so forth. All these have indicated that complex network theory is an important and useful tool, which can be applied to a wide range field.

As for the formation of widely existent scale-free phenomenon in real networks, preferential connection has commonly been considered as a key factor. Taking preferential connection as a foothold, many variations of the scale-free network model have been proposed during the recent past years. For instance, the comprehensive  multi-local-world  model  [24]which requires no global information while behaves a novel topological feature as not being complete random or complete scale-free but being somewhere between them; the local preferential attachment model [25]which is based on the common senses that people can own information easily from its local community than from outside environment; the physical position neighborhood model [10]which  mimics  the  actual communication network and  appears a  degree distribution interpolate the power-law scaling and exponential scaling; the Poisson growth model [26] which sets up the number of edges added at each step as a random variable corresponds with Poisson distribution and can generate many kind networks by controlling the random number; the weighted BA scale-free model [27] which involves the concept of weight and presents some distinguishing features with the original BA model, and so on. While the above models consider a scale-free network must be growing, some researches [28][29] proved that scale-free phenomenon can also exist in non-growth evolving networks like friendship networks and the brain functional networks in which preferential edge-rewiring process continuously occur. However, some further studies showed that preferential connection can’t be found in some scale-free networks, such as the astrophysical network [30]. Some new model has been proposed to interpret it, like the one presented in [30] and [31].

In this paper, we constructed a new scale-free network model based on random connection. The model abandons the preferential choice of vertices and meanwhile it doesn’t require global information during the evolving process, but it can still make assurance on the emergence of scale-free distribution in networks. The paper is organized as following: the new model is detailed in section 2, a theoretical analysis based on mean field theory and a numerical simulation are presented in section 3 and section 4 respectively, and conclusions are made in the last section 5.

• II.    Model

In the classic scale-free network model [13], a new vertex connects sides to old vertices according to the p (k)= у probability        ^ i , in which k is the degree of

k an old node and ^ i is the total degree of the whole network. The probability of preferential connection also said the importance of an old node in the network.

Since such preferential connection need to be in the master global information premise, it’s possibility has become scarce in real life. The more situations are under the conditions of only mastered the local information, it must be carried out to determine. Even if one can master the global information, it will become very difficult because of the processing speed and computational practice.

To make our model closer to the actual situation, We consider this case: Only obtain the information amount of an arbitrary neighbor vertex of a random vertex. As if when an individual go to a strange city, his first choose is contact his friends at the local, rather than arbitrarily ask some strangers for information.

The specific model construction is divided into the following two steps:

• 1) . Growth: Starting from a network consists of ^{m 0} vertices. At every time step we add a new vertex with ^m edges into the network.

• 2) . Random attachment: Connecting the new vertex to ^m vertices already exist in the network. Each vertex is chosen as an arbitrary neighbor of an arbitrary vertex from the network.

  

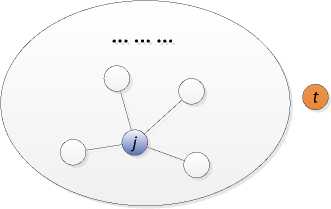
  Fig. 1: An illustration example of the model

  
  
  
  
  

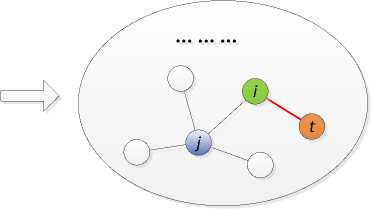
A new vertex (label with orange color, denote by ^t ) is added into network at time step ^t . It will be connected with m edges to vertices already in the network. For one of these edges, we first randomly select one vertex in the network (label with blue color, denote by ^j ), then randomly select one neighbor (label with green color, denote by ⁱ ) of this vertex, and finally create the edge linking the new vertex and the selected vertex.

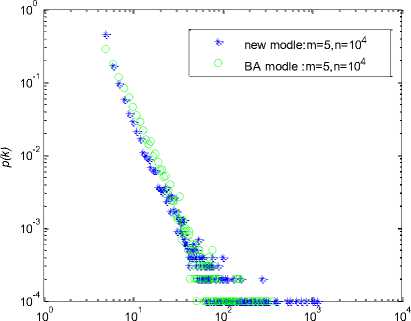
In accordance with the evolution Process of the network model, we make some simulations of the new model and the the classic BA model. When the number of add edges every time is m = 5 and the number of network evolution times is n =10 , the results are presented in Fig. 2. According to the results obtained, we can see that such a new model can be obtained BA scale distribution to express degree distribution. Compared with the classic BA model, the power-law distribution index of the new model also is 3. From another angle, the way you select an arbitrary neighbor vertex of a random vertex can completely instead of preferential connection. In other words, this new way could performance out certain preferences performance.

k

Fig. 2: Comparison between new model and classic BA model comparison

• III.    Mean Field Theory Based Theoretical Analysis

According to the model, when we connect a new vertex to an existing vertex in the network, firstly we need to select a random vertex in the network, and then select a random neighbor of the selected vertex as the target vertex to be attached to the new vertex.

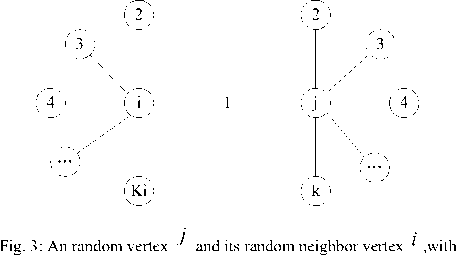
their degrees respectively are k and ⁱ

As the Fig. 3 shows, we denote the former vertex as vertex j and the later one as vertex i , and their degrees just after time step t in evolution process are presented by   j(t)  and  ki (t)  respectively. After investigating the topological feature of the vertex i and j , we make analysis as follows.

• 1) . the probability of selecting a random vertex ^j in 1

the network is m 0 ⁺ t . Since the degree of vertex ⁱ is ^{ki ( t )}, then the probability ^{p 1} of selecting a random vertex ^j which is one of neighbors of

P1=ki()- vertex i is      m0 + t .

Taking both the above two scenarios into account, we can derive the final probability of vertex i to be selected as one vertex to be connected to the new added vertex. We denote the probability as П(k (t)), and it can be represented as k (t) mo+t   1                  k

П(k, (t)) = P1 p2 =      E —P (kj (t)) = —‘—A m о +1 кдt )=1 j t)           m о +1

,

where m 0 + t i

A = E J P ( к ) к =1 ^k

Appling the mean field theory [13], the dynamic equations is

5 k: ( t )                „        k ( t )   .       k , ( t ) .

—i— = m П ( k ( t )) = m ——— A re m ——- A d t                     m₀ + 1         t

The viable of m in (2) is introduced after we take into account that each new vertex will have m edges attached to vertices that are already well connected. This also gives us the initial conditions for (2) that i(ti)  m where ti denotes the time step when vertex i is added.

Setting t to infinity, the value of A should become constant. By integrating (2), with the initial conditions, we can get k (t) = m

Assuming that we add the vertices at equal time intervals to the system, the probability density of i is

P ⁽ i ) = ¹

t

Further on, we need to consider the probability p2 of selecting a random vertex i from an arbitrary neighbor of vertex i . As shown in the model, the vertex i is a random neighbor of the vertex j , so p 2 = ITT j (t). However, p2 can’t be determined due to the fact that  j (t) remains unknown for us because vertex j is randomly selected from the network. Here, we used the mean value of p2 to fix the value. We considered the degrees of two vertices in the network are independent with each mo + t     1

p 2 = E        ⁽ k j ⁽ t ))

other. So we get       kj(t,_1 j' '         where the probability  p(k)

is a vertex in the network interacts with k other vertices.

Thus, according to (3), the network degree distribution can be derived as mm1A            mm1At

P (ki (t) < k) = P (ti > — t) = 1 —т------ kmA         kmA (m0 +1)(4)

and

_   5 p ( k ,- ( t ) <  k )     m m 1 A t   1    -(^+1)

P ( k ) =------------=

5k       (m0 +1) mA^^

Defining в = mA = m E —p (k)

k=1k      ,(6)

we can get the distribution function of the network as

- 1

p (k )=mL k-I •-*)

Through the results given by the (7), we can conclude that this distribution function meets the definition of scale-free distribution, and the distribution exponent of this network equals^{( в +} 1).

If we substitute (7) into (6), we can get the (8). It turns out that we can get the exact value of ^в through solving (8). It seems that ^в is irreverent with the networks size but related with the parameter ^m .

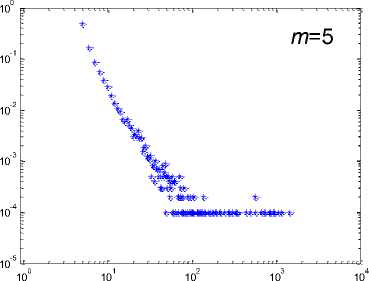
Then, we conduct simulation with four network instances. The four network instances all evolves themselves with time span of ⁿ = ¹⁰ , but they have distinguishing value of parameter ^m . Their final degree distributions are recorded in Fig. 5.

в = m ^{( e} - ^{+ 1)}

to

Z k

k =1

-( в "1 +2)

IV. Simulation Research

According to the theoretical analysis in section 3, we solved the value of ^в under different ^m and conducted simulation with four network instances respectively plotted the result in Fig. 4 and Fig. 5.

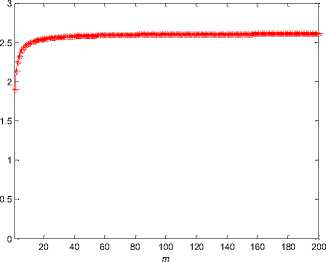
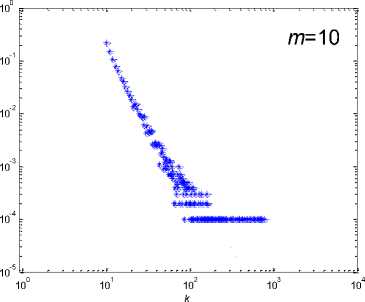
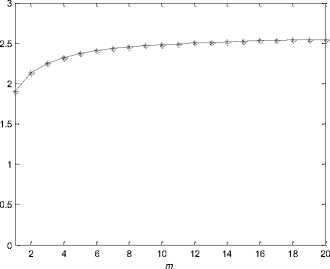
Fig. 4: The value of ^в under different ^m

In the Fig. 4, it shows that the value of ^в increases with different ^m accordance with (8). When ^m changes large from 0 to 200, we get a stable value of ^в quickly. The first figure shows when the correlation between ^в and ^m , the range of ^m is set as from 0 to 200. The second figure narrows ^m ’s range into from 0 to 20.

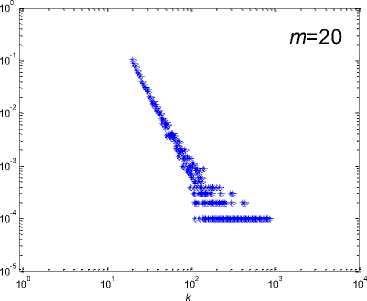
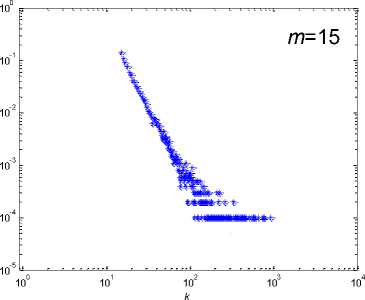
Fig. 5: The degree distribution of four different network instances

. „  .   ,           .   . р           m, = 20                    .

All instances start from a 0      fully-coupled network and evolves themselves n = 10 time step. The values of parameter m for these instances are set as m  5, 10, 15, 20     respectively.

The    blue

distributions are degree distributions and the red curves are theoretical distributions.

Although it need some time for ^в in a network to reach steady, we can see that the time could be momentary because the degree distributions all fit the final steady ones inferred from theoretical analysis well. On the other side, it seems the degree distribution is better fitted with the theoretical one with the increasing of ^m . This is obvious, because with larger ^m , the value of ^в will reach a steady state much quicker. All in all, the simulation has proved that our model based on random selection indeed can generate scale-free networks.

• V. Conclusion

Our study finds out that random attachment in network can also generate scale-free network. Through analysis and simulation experiments, we see that: using the way of selecting one arbitrary vertex from an arbitrary vertex’s neighbors will make the selected vertex be more probable to be a vertex with large degree. For example, in the network of friends, your friends have always more friends than you [32][33]. It also explains this way of selecting vertex has a certain preferential features.

On the other hand, our model does not require one to know the global information of a network. It can operate with only some local information in a network, namely the neighborhood is a particular vertex. This feature is more consistent in the real network. In particular, we know it is impossible to master the global information in the Internet and networks with huge scale. So in this way not only improve the computational efficiency but also makes the feasibility of the network can be improved.

From Fig. 4, we can see the exponent of the scale-free distribution in our model is located in 1.90~2.61 when ^m ranges from 1 to 200. This has been compliant with ones of many real networks ^[28]. This indicates the scheme we mentioned in this paper may play a role in these networks, and it helps us understand these networks.

In sum, we study the network characteristic of a random neighbor of a random vertex in complex networks and find that it is similar to the vertex selected by preferential connection mechanism in networks. The presented results help us better understand the speciality of complex networks and design an efficient network model to produce scale-free property. We have reason to believe that the choice of vertex to generate scale- free conditions for meaningful research. Network characteristics manifested by such way will also have the other networks to provide new ideas and methods.

Acknowledgements

The work is supported by the National Natural Science Foundation of China under Grant No. 60874080, the commonweal application technique research project of Zhejiang Province under Grant No.2012C23126 and the Open Project of State Key Lab of Industrial Control Technology of Zhejiang University under Grant No. ICT1107.