Ранняя диагностика геомагнитных бурь на основе наблюдений систем космического мониторинга

Солнечные корональные выбросы массы (КВМ) оказывают существенное воздействие на магнитосферу Земли, вызывают магнитные бури и приводят к возможным большим проблемам при функционировании технических и биологических объектов. Ранняя диагностика геомагнитных бурь является актуальной научной задачей [Handbook of Cosmic …, 2015; Solar Eruptions and …, 2006]. По данной проблематике имеются две категории публикаций по моделям, связанным с диагностикой и предсказанием времени прибытия КВМ. К первой категории относятся публикации с описаниями моделей, в которых реализуются подходы, основанные на уравнениях магнитной гидродинамики плазменных образований, ко второй — публикации, в которых рассматриваются различные варианты нелинейных моделей движения КВМ.

В cтатье [Odstrcil, 2003] описывается модель ENLIL, используемая NASA для прогнозов в гелиосфере, которые осуществляются путем решения уравнений магнитной гидродинамики. Основной особенностью данной модели является отсутствие в ней механизма разогрева солнечной короны, который описывается феноменологически. Точность прогнозов прибытия КВМ к Земле по этой модели составляет около восьми часов. В статье [Jin et al., 2017] описывается модель BATSRUS, также основанная на уравнениях магнитной гидродинамики, но включающая механизм разогрева солнечной короны за счет альфвеновской турбулентности. Благодаря этому модель последовательно описывает не только гелиосферу, но и солнечную корону. Описан также инструмент EEGGL, позволяющий по оптическим и магнитным наблюдениям задавать начальные условия для КВМ, дальнейшее движение которого через корону и гелиосферу может быть рассчитано согласно уравнениям модели. На сайте [] представлена модель WSA-ENLIL, являющаяся усовершенствованной версией [Odstrcil, 2003]. Подходы, использующие решения уравнений магнитной гидродинамики и основанные на детальном рассмотрении физики процессов в гелиосфере, потенциально могут обеспечить эффективное решение задачи ранней диагностики.

В статье [Owens, Cargill, 2004] рассмотрены три феноменологические модели распространения КВМ, позволяющие вычислять время прибытия. В первой модели считается, что выброс движется с постоянным ускорением на всем пути от Солнца до орбиты Земли. Во второй предполагается, что до некоторого расстояния, меньшего радиуса земной орбиты, выброс движется равноускоренно, а далее равномерно. В третьей модели считается, что ускорение выброса пропорционально разности скоростей выброса и окружающего солнечного ветра, коэффициент пропорциональности зависит от расстояния до Солнца по степенному закону. Первая модель содержит два параметра (начальную скорость и ускорение), вторая — три параметра (начальную скорость, ускорение и расстояние, на котором ускоре- ние прекращается). Третья модель содержит четыре параметра (начальную скорость, степень и множитель в коэффициенте увлечения и асимптотическую скорость солнечного ветра). В [Gopalswamy et al., 2000] на основе 28 межпланетных событий КВМ разработана эмпирическая формула времени прибытия КВМ, работа которой исследована: показано, что ее предсказательные характеристики лучше для быстрых КВМ, чем для медленных. В работе [Mittal, Narain, 2015] для вычисления времени прибытия используется простейшая модельная линейная зависимость между скоростью на вылете КВМ от Солнца и временем распространения до Земли; предлагаются к рассмотрению случаи медленных (<500 км/с) и быстрых (>500 км/с) КВМ. Статья [Michalick et al., 2004] содержит описание подхода к получению скорости КВМ, основанного на решении специальной оптимизационной задачи.

И, наконец, материал [Gopalswamy, 2016] является обзором истории изучения КВМ, в основном сконцентрированным на данных наблюдений и их систематизации. Вопросы диагностики и соответствующих моделей распространения КВМ подробно не обсуждаются.

К рассматриваемым здесь измерительным системам космического мониторинга относятся спутниковая система SOHO [Brueckner et al., 1995; Delaboudi-niere et al., 1995] (проект NASA и ESA (European Space Agency)); спутниковая система STEREO [Howard et al., 2008] (проект NASА) и мюонный годоскоп (МГ) «Ураган» [Barbashina et al., 2008; Yashin et al., 2015] (проект НИЯУ МИФИ (РФ)).

Измерительная спутниковая система SOHO находится в точке Лагранжа, примерно в 1.5 млн. км от Земли. На ней установлены приборы наблюдения КВМ: ультрафиолетовый телескоп EIT (Extreme Ultraviolet Imaging Telescope) и коронограф LASCO (Large Angle and Spectrometric Coronagraph). EIT позволяет получать снимки на длинах волн 17.1, 19.5, 28.4 нм (линии железа) и 30.4 нм (линия гелия). Он может также снимать весь солнечный диск, его поле зрения составляет 1.5 R _@ (здесь R _@ — солнечный радиус), разрешение 1024×1024 пиксела. LASCO представляет собой набор из трех коронографов с перекрывающимися полями зрения: от 1.1 до 3, от 1.5 до 6 и от 3.7 до 30 R _@ . Коронографы работают в видимом диапазоне с разрешением 1024×1024 пиксела.

Измерительная спутниковая система STEREO (Solar TErrestrial RElations Observatory) состоит из двух спутников, выведенных на орбиты, близкие к орбите Земли, и вращается вокруг Солнца с периодами 346 и 388 дней. Радиусы орбит отличаются от радиуса орбиты Земли примерно на ±4 %, так что первый спутник постепенно удаляется от Земли вперед по орбите, а второй — назад. На борту каждого спутника STEREO установлены приборы наблюдения КВМ: модуль SECCHI (Sun Earth Connection Coronal and Heliospheric Investigation) — ультрафиолетовый телескоп EUVI (Extreme Ultraviolet Imager) с полем зрения до 1.7 R _@ , два коронографа с полями зрения от 1.4 до 4 и от 2.5 до 15 R _@ и два широкоугольных телес-

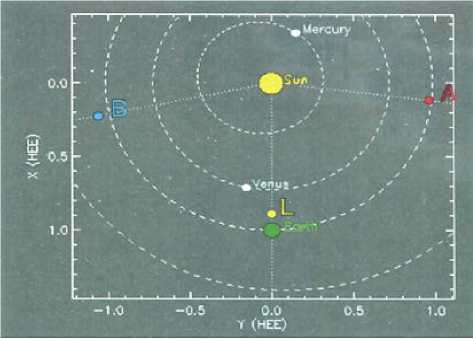
Рис. 1. Орбиты планет, положения Земли, Солнца, систем SOHO и STEREO

а

б

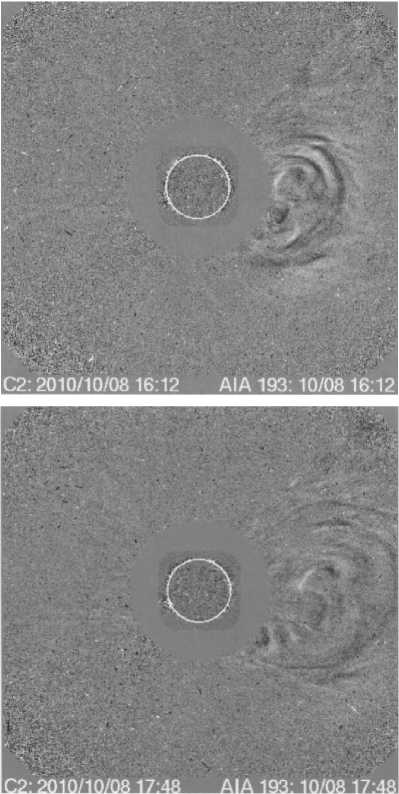
Рис. 2. Снимки КВМ со спутниковой системы SOHO 08.10.2010, 16:12 ( а ), 17:48 ( б )

копа, покрывающих углы от 4° до 24° и от 19° до 89° от Солнца (15-84) R _@ и (66-318) R _@ в плоскости орбиты Земли. Все приборы имеют разрешение 2048×2048 пикселов.

На рис. 1 штриховыми линиями изображены орбиты, точками — положения Земли, Солнца, измерительных систем SOHO (L) и STEREO (А, В), соответствующие дате 08.10.2010 [ where].

На рис. 2, а, б показаны изображения КВМ, полученные коронографом LASCO (SOHO) [https://cdaw. ]. По изображению рис. 2, а прибли-

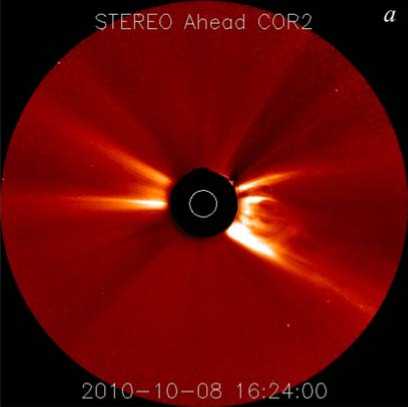
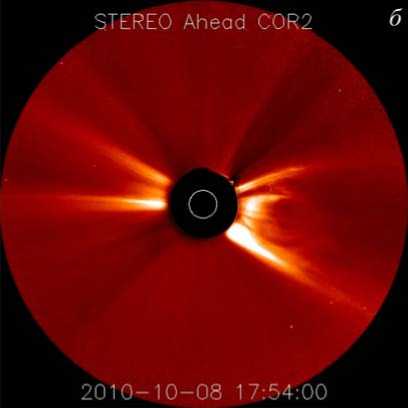
Рис. 3. Изображения КВМ со спутниковой системы STEREO 08.10.2010, 16:24 ( а ) и 17:54 ( б )

женно может быть оценено положение центра КВМ относительно центра Солнца: видно, что в первом случае центр КВМ находится на расстоянии =3.4R _@ , во втором случае на рис. 2, б центр КВМ смещен на расстояние =4.2 R _@ .

На рис. 3, а, б представлены изображения КВМ от коронографа системы STEREO c полем зрения (2.5^15)R@ []. По снимкам рис. 3, а, б может быть определено приближенное положение центров КВМ относительно центра Солнца: в первом случае центр КВМ находится на расстоянии =5.1 R@ от центра Солнца, во втором случае центр КВМ смещается на расстояние =7.3 R@.

Наблюдения систем SOHO и STEREO могут быть представлены последовательностями дискретных двумерных функций S ₁( i , j , T ₁ k ), S ₂( i , j , T ₂ k ), где индексам ( i , j ) ∈ S 01 , ( i , j ) ∈ S 02 соответствуют дискретные наблюдения азимутальных и зенитных углов; S 01 , S 02 — области определения индексов; T 1 , T 2 — интервалы дискретности наблюдений. Алгоритм автоматического определения угловых положений КВМ — оценки азимутальных φ°( T _{1, 2} k ) и зенитных ϑ°( T 1, 2 k ) углов — для данных систем может быть сформирован в первом приближении на основе вычисления соответствующих моментных характеристик функций S ₁( i , j , T ₁ k ), S ₂( i , j , T ₂ k ):

• < ( T ,2 k) = ( £ iS^i , j , T ,2 k ))/ ^ S 1,2 ( i , j , T 1,2 k ), i , j ∈ S _{01, 2} i , j ∈ S _01,2

• 9 ° (T_V 2 k ) =

• = ∑ jS 1 2 ( i j T 1 2 k ) ∑ S 1 2 ( i j T 1 2 k ). ⁽¹⁾ i j ∈ S _{01 2} i j ∈ S _{01 2}

Для плоского случая погрешность определения положения центра КВМ может составить величину Δ R SC =α R S где R S — радиус Солнца, α — заданный коэффициент. Погрешность углового азимутального положения КВМ может быть определена величиной Δφ 1 2 =Δ R SC / R SE где R SE — расстояние Солнце — Земля. Пусть α=3.0 R S =0.004652 R SE , тогда имеем оценку погрешностей угловых положений Δφ 1 2 ≈0.795°.

Измерительная наземная система «Ураган» на основе МГ осуществляет наблюдения функции угловых распределений интенсивностей мюонных потоков. Указанные наблюдения S ₃( i j T ₃ k ) i =1 … N ₁ j =1 … N 2 размещаются в информационных МГ-мат-рицах с шагом по времени T ₃=1 мин. Наблюдения МГ реализуются в диапазоне 0°≤φ≤360° и 0°≤ϑ≤76° по азимутальным и зенитным углам относительно земной системы координат с угловой дискретностью в Δφ=4° Δϑ=1°; каждая МГ-матрица имеет размерность ( N 1 N 2 ) N 1 =90 N 2 =76. Угловое положение центра возможного КВМ может быть оценено на основе определения в МГ-матрицах аномальных угловых областей, связанных со снижением интенсивности мюонных потоков при возникновении КВМ-образований с использованием формул, аналогичных (1).

Рисунок 4 показывает пример вычисления | модуля Δ S ₃( i j )| величины снижения интенсивностей мюонных потоков, полученных на основе цифровой обработки последовательностей МГ-матриц. Время наблюдения — 06.06.2015 15:30.

Видно, что аномальная область для МГ-матрицы с максимальным значением модуля снижения интенсивности в данном случае может быть определена дискретными координатами 51≤ i ≤52 30≤ j ≤31 что соответствует азимутальным и зенитным углам 204°≤φ _i ≤208° 30≤ϑ j ≤31°. При этом погрешность определения углового положения КВМ, наблюдаемого системой «Ураган» приближенно может составить величину Δφ 03 ≈(4²+1²)^1/2=4.12°. С помощью первичной цифровой обработки последовательности N 0 =10÷15 информационных МГ-матриц может быть достигнуто снижение угловых погрешностей до значений Δφ₃≈Δφ₃₀/√ N ₀=(1.06°÷1.31°).

Необходимо отметить, что с учетом принятых допущений, погрешность определения углового положения КВМ-образований от рассматриваемых измерительных систем может принять значение Δφ 1 2 3 ≈(0.5°–1.5°). Следует заметить, что на сегодня отсутствуют реальные наблюдения с указанных систем; для расчетов в дальнейшем будем использовать модельные наблюдения.

В статье ставится задача ранней диагностики геомагнитных бурь на основе разработки метода и алгоритма цифровой обработки угловых наблюдений с измерительных систем космического мониторинга с учетом модели декартовых координат движений КВМ. С этой целью здесь предлагается процедура

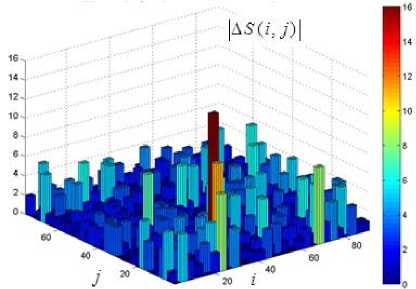
Рис. 4. Пример модуля функции величины снижения интенсивностей мюонных потоков принятия решения о потенциально опасной близости КВМ к Земле, которая базируется на введенной функции прогноза расстояния между Землей и центром КВМ. Разрабатывается алгоритм оценивания параметров уравнений движения системы Земля — центр КВМ, основанный на минимизации функционала обобщенной триангуляции. Вычисляется функция прогноза расстояния и реализуется принятие решения по ранней диагностике путем сравнения минимального значения функции прогноза с заданным безопасным расстоянием Земля — центр КВМ. Для оценивания эффективности ранней диагностики применяется статистическое моделирование, основанное на моделях движений КВМ и модельных наблюдениях. Определяются оценки вероятностей ошибок процедуры принятия решений по ранней диагностике геомагнитных бурь.

Настоящая работа допускает возможность оценки угловых положений центров КВМ на основе цифровой обработки информации с измерительных систем космического мониторинга, расположенных в космическом пространстве и на Земле. Указанное оценивание может быть осуществимо, когда КВМ-образования находятся на расстоянии ≈0.05–0.2 а.е. от поверхности Солнца (ближняя зона). В данном случае КВМ-образования имеют небольшие угловые размеры для наблюдений с орбиты Земли и их можно с определенными допущениями принимать в виде перемещающихся в ближней зоне почти точечных областей [Xue et al. 2005].

Предлагаемое в статье решение по ранней диагностике отличается по своей постановке от [Owens Cargill 2004; Gopalswamy et al. 2000; Mittal Narain 2015; Michalick et al 2004]. В статье для выработки решений заложена возможность применения реалистичной модели движения КВМ и использования текущих угловых наблюдений за КВМ. Подход [Odstrcil 2003; Jin et al. 2017], связанный с применением модельных трехмерных уравнений магнитной гидродинамики, позволяет учитывать большее число характеристик солнечного ветра и КВМ по сравнению с феноменологическими моделями, но требует чрезвычайно больших вычислительных ресурсов.

• 1.    МЕТОД РАННЕЙ ДИАГНОСТИКИ ГЕОМАГНИТНЫХ БУРЬ

Геометрическая схема движений системы Солнце — центр КВМ — Земля — измерительные системы кос-

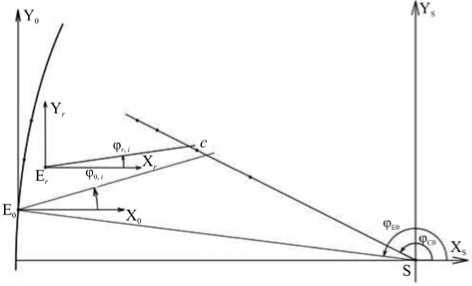
Рис. 5. Геометрическая схема движения системы Солнце — центр КВМ — Земля — измерительные системы космического мониторинга

R Ecmn = R ec ( c ° , t ° ( c ° )). (3)

Метод ранней диагностики геомагнитных бурь реализуем на основе процедуры принятия решения для проверки неравенства R E _Cmin S R _EC, где R _EC — задаваемое минимально безопасное расстояние Земля — КВМ. В случае выполнения неравенства будем принимать решение, которое состоит в том, что центр возможного КВМ находится достаточно близко от Земли и данный КВМ представляет собой потенциальную опасность с точки зрения возникновения геомагнитной бури. В случае невыполнения неравенства будем принимать противоположное решение.

мического мониторинга для рассматриваемой задачи в 2D-случае показана на рис. 5.

Солнце (S), поместим в центре неподвижных прямоугольных декартовых координат X_sSY_s. Центр КВМ обозначим C. Будем считать, что E 0 и X 0 E 0 Y 0 — это Земля и связанные с ней оси координат, параллельные X s SY s ; E r и X r E r Y r — измерительные системы космического мониторинга с соответствующими осями координат, r =1 , …, r .

Пусть x _E( t ), y _E( t ) — декартовы координаты Земли, которые будем считать точно известными. Зададим нелинейные функции общего вида x CM ( c , t ), y CM ( c , t ), которые примем в качестве моделей декартовых координат перемещающегося центра КВМ, зависящих от вектора параметров c^T =( c 1 , …, c n ₀). В частности, эти функции могут быть полиномиальными — линейными, параболическими и т. д.; выбор функций моделей позволяет сформировать в достаточной степени произвольные траектории движений КВМ в гелиосфере. Положим, что на некотором интервале времени ( t ₀, t f ) по наблюдениям угловых координат КВМ с измерительных систем и с учетом моделей декартовых координат КВМ могут быть вычислены оценки вектора параметров c° и, соответственно, функций координат для центра КВМ x _CM( c° , t ), y _CM( c° , t ). Реализуем прогнозирование положения центра КВМ, введем функцию расстояния между Землей и центром КВМ

R EC ( C ° , t ) =

• = V( x E ⁽ t ) - x CM ⁽ c ° , t ) ) 2 + ( У E ⁽ t ) - У CM ⁽ c ° , t ) ) 2 ,

• 1 0 S t S t f .                                     (2)

• 2.    АЛГОРИТМ ОЦЕНИВАНИЯ ПАРАМЕТРОВ МОДЕЛЬНЫХ ФУНКЦИЙ ДВИЖЕНИЙ ЦЕНТРА КВМ

  • 2.1.    Рассмотрим в общем виде алгоритм оценивания параметров модельных функций движения центра КВМ. Обратимся к рис. 5. Положим, что наблюдения производятся в моменты времени t r , i и им соответствуют φ _{r , i} — угловые наблюдения за центром КВМ, приведенные к системам координат X _r E _r Y _r и отсчитываемые от оси E _r X _r против часовой стрелки, r =0, 1, …, r –1; i =0, 1, …, N r –1 , где N r — число наблюдений, произведенных измерительной системой с индексом r ; оси системы координат X r E r Y r перемещаются параллельно осям системы координат X s SY s .

Для известной численной оценки вектора параметров c ° функция R EC ( c° , t ) является полностью определенной. Вычислим минимальное прогнозируемое расстояние между Землей и центром КВМ. Примем величины временных границ t 0 , t f , для которых функция R _EC( c° , t ) из (2) на интервале ( t ₀, t f ) заведомо достигает своего минимума. Найдем минимум функции R _EC( c °, t ) на рассматриваемом интервале, вычислим соответствующее время t° ( c° ) и R EC ( c° , t ( c° )) — величину минимального прогнозируемого расстояния:

t ° ( c ° ) = arg

min R _c( c ° , t ) , ( t 0 s t S t f

Зависимости координат Земли x E ( t r , i ), y E ( t r , i ) от моментов времени t r , i определим с помощью следующих функций времени

φE(tr, i)=ωEtr, i+φE0, xE(tr, i)=REScosφE(tr, i), yE(tr, i)=RESsinφE(tr, i), (4) где φE0, ωE0, RES — начальный угол, угловую скорость движения Земли по орбите вокруг Солнца и расстояние Солнце — Земля считаем заданными для (4). Координаты центра КВМ для времен tr,i вычислим с помощью моделей заданного вида xCM(c, tr,i), yCM(c, tr,i) из п. 2. Запишем выражение для функционала обобщенной триангуляции Sr (c, ф) в виде двойной суммы, физический смысл которой очевиден:

r

Sr(c, ф) = ^аr х r = 1

^r- 11 х^  ф r , i i =0 .

— arctg

2 (5)

У CM⁽ с , t r , i ) - У E⁽ t r , i )

^:CM^{( c} , t r , i ) - x E⁽ t r , i )

,

где φ — блочный вектор угловых наблюдений, α _r — весовые коэффициенты, учитывающие различные точности угловых наблюдений от рассматриваемых измерительных систем. Оценим вектор параметров c° с помощью минимизации функционала по ширине (5) по вектору параметров c e C , где C — ограничивающее множество c° = arg { min S r ( c , ф ) } .

Множество C образуем системой неравенств cn, min≤cn≤cn, max, n = 1, …, n0. Применим поисковый метод минимизации нулевого порядка на основе прямого перебора для отыскания оптимальных оценок вектора параметров [Singiresu, 2009]. Организацию перебора — выработку дискретизованных параметров cn(kn) — произведем на основе следующих соотношений:

c n ( k n )= c

n , min

+Δ c n ( k n –1),

Δ c n =( c n , max – c n , min )/( K fn –1), K fn >1, (6) где Δ c_n — шаг перебора по параметрам, k_n =1, …, K f _n , n = 1, …, n 0 . Благодаря введенной дискретизации функционал (5) представим зависимым от k 1 , k 2 , …, k m

и нахождение оптимальных параметров c ° в данном

случае произведем на основе минимизационного поискового перебора по целочисленным переменным

⁽ k ² ,..., к^о ) = arg { min    S 1⁽ к,..., к

0                  k n , n = 1,..., n о                        0

ф ) } ,

c n = c n ^{( k} 1 ,..., ^k n ₀), n =1, -, n 0 .

2.2. Разберем случай одной измерительной системы, когда Г = 1, и определим моменты времени t0, i=ti, i=0, 1, …, N–1. Для функций времени координат Земли xE(ti), yE(ti) воспользуемся формулами (4). Рассмотрим простейший пример модели декартовых координат центра КВМ в виде линейных функций xCM(c, ti)=RC0+VC0ti)cosφC0, yCM(c, ti)=

=( R C0 + V C0 t i )sinφ C0 . (8)

Для (8) центр КВМ перемещается равномерно и прямолинейно со скоростью V _C0 под углом φ_C0, который отсчитывается от оси SX s против часовой стрелки и в начальный момент времени находится на расстоянии R C0 от Солнца. В данном случае, представим трехмерный вектор параметров модели следующим образом – c^T =( c ₁, c ₂, c ₃), c ₁= V _C0, c ₂=φ_C0, c ₃= R _C0.

Для заданных t_i и наблюдений угловых положений φ _i центра КВМ, i =0, 1, …, N –1 функционал триангуляции запишем в виде одинарной суммы

S i ( c , ф )

х -11              У ( c , t - У г ( t ) I

= Zk —arctg CM i E i I i=0 V             xCM( c, ti xE( ti) J

.

КВМ c ° = V C₀ , c 2 =ф С₀ , c ₃ ² = R C ₀, полученных с использованием (9).

Для дискретных моментов времени t_l , t_l = t f ₀+Δ t ( l –1), с шагом Δ t =( t f – t f ₀)/( L f –1) вычислим, используя (2), последовательность значений функции прогноза расстояния между Землeй и центром КВМ R _EC( c °, t_l ), l =1, …, L f :

^R EC ^{( c} , t l ) =

= V ⁽ x E ⁽ t l ) ^{— ( R} C0 + ^V C0 t l ) cos ^ф С0 ) +     ⁽¹⁰⁾

V ^{+ (} y E ⁽ t l ) ^{— (} R C0 ^{+ V}C0tl ) ^{sin ф} С0 ) .

Для последовательности (10) найдем минимальное прогнозируемое расстояние Земля — КВМ RECmin l° = arg !, min REC (c°, tl )L l=1,..., Lf

R ECmin = R ( c , t ° ).

Процедура принятия решения состоит в проверке неравенства R E _Cmin <  R _EC. При выполнении этого неравенства будем принимать решение, что центр КВМ находится достаточно близко от Земли и данный КВМ представляет собой потенциальную опасность с точки зрения возникновения геомагнитной бури. В случае невыполнения неравенства будем принимать противоположное решение.

Если оценки вектора параметров c° значительно отличаются от исходного вектора параметров c , то при реализации процедуры принятия решений возможны ошибки первого и второго рода.

1. При выполнении условия R _ECmin( c ) >  R _EC будет иметь место неравенство R _ECmin ( c° ) <  R _EC, соответствующее случаю ложной КВМ-тревоги, который характеризуется условной вероятностью α

«= P {RECmin(c° ) < Rec } для

R ECmin ( c ) >  R ec .                        (11)

Оптимальные параметры c n , n = 1, 2, 3 для модельных функций координат центра КВМ представим аналогично (7)

(k°, k2', k°) = arg min S (kx, k2, k3, ф) , k1,k2,k3

< = с ( k ° ), n = 1,2,3.                (9)

2. При выполнении условия R _ECmin ( c ) <  R _EC будет иметь место неравенство R _ECmin ( c° ) >  R _EC, соответствующее случаю пропуска КВМ, который характеризуется условной вероятностью

P = P { R ECmin ( c° ) >  R EC }

для

Данный пример здесь рассмотрен ввиду малых временных затрат, требуемых на вычисления параметров модели (8). Разумеется, более реалистичные модели движения КВМ в виде параболических и других функций вполне могут быть вычислены при больших временных затратах.

^R ECmin ⁽ c ) <  ^R EC .

Очевидно, что величина 1–β представляет собой вероятность правильного решения по ранней диагностике.

3. ПРИНЯТИЕ РЕШЕНИЙ

ПО РАННЕЙ ДИАГНОСТИКЕ ГЕОМАГНИТНЫХ БУРЬ

Принятие решений по ранней диагностике геомагнитных бурь сформируем на основе оценок параметров модельных функций движений центра

4. ОЦЕНИВАНИЕ

ЭФФЕКТИВНОСТИ ПРОЦЕДУРЫ

ПРИНЯТИЯ РЕШЕНИЙ

ПО РАННЕЙ ДИАГНОСТИКЕ

ГЕОМАГНИТНЫХ БУРЬ

Оценивание эффективности процедуры принятия решений по ранней диагностике геомагнитных бурь

реализовывалось посредством технологии статистического моделирования.

Задавалась последовательность моментов времени t_i , t_i =0, 1, …, N –1 , численные значения начального условия и констант φ E0 , ω E , R ES и исходные параметры модельных функций декартовых координат центра КВМ c 1 = V C0 , c 2 =φ C0 , c 3 = R C0 для вычисления последовательности декартовых координат Земли x E ( t i ), y E ( t i ) по (4) и модельных декартовых координат КВМ x CM (c, t ), y CM (c, t ) по (8).

Вычислялась последовательность угловых положений φ 0, i центра КВМ в системе координат x 0 E 0 y 0 для моментов времени t i , t i =0, 1, …, N –1.

_Фо , = arctg y ^cm( c , t i ) — y ^{e (} t i ) .

• ^0, x cm ( c , t ) — У e ( t )

Для проведения статистического моделирования формировались реализации последовательностей модельных случайных погрешностей δφ s , i , распределенных по нормальному закону с нулевым математическим ожиданием и заданным среднеквадратичным отклонением (СКО) σ, i =0, 1, …, N –1, s =1, …, M 0 , где M 0 — число реализаций. Формировались реализации угловых наблюдений φ s, i =φ 0, i +δφ s, i , i =0, 1, …, N –1, которые образовывали векторы наблюдений φ ^T s =(φ s, 0 , φ s, 1 , …, φ s, N –1 ), s =1, …, M 0 .

Выполнялись решения M 0 задач оптимизации (9) с наблюдениями φ s . Для организации прямого перебора задавались число переборов K f _n , n =1 , 2, 3, нижние границы поиска c 1, min , c 2, min , c 3, min шаги перебора Δ c ₁=Δ V _C0, Δ c ₂=Δφ_C0 и Δ c ₃=Δ R_{C 0}, вычислялись c n , max с использованием (6). Находились оптимальные параметры c j , ₅ , n =1, 2, 3, 5 =1, ..., M ₀ по (9). Для статистического моделирования задавалось число реализаций M 0 =100. Принимались величины K f _n =100, n =1, 2, 3, c _{1, min}= 250·10³ м/с, c 21, min =145°, c 22, min =120°, c 3, min =75·10⁹ м/с. Для надежной работы алгоритма — достижения приемлемой точности оценивания оптимальных параметров — оказалось необходимым производить минимиза-ционный перебор с достаточно малым шагом: использовались шаги перебора Δ V _C0=5000 м/с по скорости, Δφ С0 =0.5° по углу и Δ R C0 =1.5·10⁶·10³ м по начальной дальности.

Моменты времени наблюдений для проведения расчетов определялись соотношением t_i = t _H+ T ( i –1), t _H=0_H T =0.25·3600 c, i =0, 1, …, N –1 . Были приняты значения начального угла φ_E0=180° и констант ω E =2π/(365·24·3600) c ^–1, R ES =150·10⁹ м. Задавались численные значения исходных параметров c 1 = V C0 =500·10³ м/с, c 3 = R C0 =0.1 R ES .

Число наблюдений N , угол c 2 =φ C0 и значения заданных безопасных расстояний R _EC варьировали в процессе статистического моделирования.

Порядок вычисления оценок вероятностей ошибок α°β° состоял в проведении этапов:

• 1.    Вычисления для задаваемого исходного вектора параметров c величины прогнозируемого минимального расстояния R ECmin ( c ).

• 2.    Вычисления реализаций оценок векторов параметров c° и оценок величин минимальных рас

• 3.    Вычисления оценок вероятностей α° и β° с помощью сравнения R _ECmin( c j ) и заданного значения R _EC . При этом возможно следующее:

стояний R ECmin ⁽ c ; ), 5 =1, .., М .

Ошибки первого рода — случай, когда в реальности имело место соотношение R _ECmin( c ) >  R _EC; подсчитывалось число событий, когда R e_C min ( c j ) — R _EC и формировалась оценка вероятности ложной тревоги α° на основе (11), с использованием функции sign( x )=1 для x >0 и sign( x )=0 для x ≤0:

1M а = ^ sign ( REC - REC min(c5 ) ).

^M 5 = 1

Ошибки второго рода — случай, когда в реальности имело место соотношение R _ECmin ( c ) <  R _EC; подсчитывалось число событий, когда R _ECmin( c _s°) >  >  R _EC, и формировалась оценка вероятности пропуска β° с использованием (12):

1M р° = M Е sign ( RECmin (c5 ) - REC ).

По величине 1–β° оценивалась вероятность правильного решения по ранней КВМ-диагностике геомагнитной бури.

На рис. 6, 7 представлены результаты вычислений оценок вероятностей α°, 1–β° ложных тревог и правильных решений по ранней КВМ-диагностике геомагнитной бури в зависимости от значений СКО угловых погрешностей наблюдений σ. Число наблю-

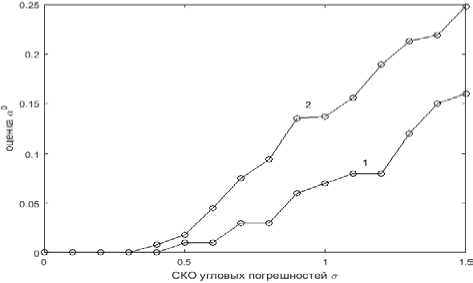
Рис. 6. Оценка вероятности α°ложного решения по ранней диагностике геомагнитной бури в зависимости от СКО угловых погрешностей σ

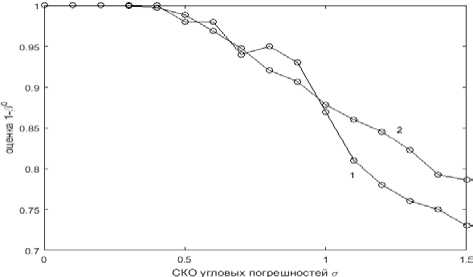
Рис. 7. Оценка вероятности 1–β° ложного решения по ранней диагностике геомагнитной бури в зависимости от СКО угловых погрешностей σ дений принималось равным N=160. Кривые с индексами 1, 2 соответствуют двум значениям безопасной дальности REC1 = 20 ⋅109 м, REC2 = 60 ⋅109 м. Для вычисления α°, 1–β° для кривых с индексом 1 приняты значения углов КВМ c21=145°, c22=170°, кривых с индексом 2 — c21=156°, c22=151°.

Видно, что для угловых погрешностей с σ≈(0.5°– 1.5°) и безопасной дальности R _EC1 вероятности ложных и правильных решений составляют вполне приемлемые для практики значения α°≈0.08, 1–β°≈0.85; для значений R _EC2 характеристики диагностики по вероятностям ложных решений ухудшаются и принимают величины α°≈0.15, по вероятностям правильных решений, практически, не меняются — 1–β°≈0.83.

На основе анализа результатов статистического моделирования для числа наблюдений N _1,2=20, 40, R _EC2 = 60 ⋅ 10⁹ м и c ₂₁=156° были получены оценки вероятностей ложных решений, которые возрастали до значений a l ® 0.25, a 2 ® 0.38 для диапазона угловых погрешностей σ≈(0.5°–0.7°). Для малых N обеспечение приемлемых характеристик ранней диагностики может быть реализовано путем снижения угловых погрешностей наблюдений, достижимое на основе возможного усовершенствования подхода обобщенной триангуляции.

Результаты статистического моделирования оценок вероятностей показали, что предложенный метод и алгоритм ранней диагностики геомагнитных бурь оказались удовлетворительными.

ЗАКЛЮЧЕНИЕ

• 1.    Разработанные метод и алгоритм ранней диагностики геомагнитных бурь на основе цифровой обработки угловых наблюдений с измерительных систем космического мониторинга с учетом моделей движений центров КВМ оказались удовлетворительно работоспособными.

• 2.    Использованный в статье подход к ранней диагностике, основанный на обобщенной триангуляции, является адекватным рассматриваемой задаче и допускает возможное усовершенствование.

• 3.    Статистическое моделирование, основанное на линейной модели движения КВМ и модельных наблюдениях, подтвердило возможность достижения приемлемой точности оценивания параметров модельных уравнений движений КВМ.

• 4.    Оценки вероятности ошибок принятия решений, произведенные на основе статистического моделирования, подтвердили, что предложенный метод и алгоритм ранней диагностики геомагнитных бурь достаточно эффективны. Так, для СКО σ≈(0.5°–1.5°) и при безопасном расстоянии R _EC1 = 20 ⋅ 10⁹ м вероятности ложных тревог и правильных решений составляют вполне приемлемые для практики значения α°≈0.08, 1–β°≈0.85.

Работа выполнена при поддержке Российского научного фонда (проект № 17-17-01215).