Расчет деформирования геометрически нелинейной плоской конструкции из идеально пластичного материала

В настоящее время в механике сплошной среды имеется значительное количество различных мер напряжений (тензор напряжений Коши [1–3], тензоры Пиолы–Кирхгофа первого и второго рода [2, 3]) и деформаций (тензоры Коши–Грина, Грина–Лагранжа, Альманси, Генки и т.д.) [1– 5]. Такое разнообразие, конечно, дает определенную свободу в создании новых и усовершенствовании уже имеющихся моделей расчета конечных деформаций конструкций. Однако в большинстве случаев понимание физического смысла соотношений, используемых в этих моделях, затруднено, особенно, когда речь идет о конструкциях из неупругого материала, где кроме геометрической нелинейности имеет место физическая. Целью данной работы является разработка такой модели расчета конечных деформаций неупругой конструкции (в качестве примера выбран идеально пластичный материал), которая была бы основана на тензорах, наиболее понятных с точки зрения физического смысла их координат, а именно: на тензоре напряжений Коши σ и тензоре инженерной деформации ε , наследуемом из геометрически линейного подхода.

Основные соотношения расчетной модели

Предложенная модель основана на методе конечных элементов, где элементы представляют треугольные симплексы. В рамках каждого элемента поле смещений является однородным и линейным, что обуславливает постоянство полей напряжений и деформаций. Однородность деформированного состояния элемента означает наличие линейной связи между начальными векторами волокон l ₀ этого элемента и векторами его волокон l в деформированном состоянии:

l = F ⋅ l 0 .                                                      (1)

Оператор этой связи – тензор дисторсии F , координаты которого определяются векторами смещений узлов элемента. Выражение для дисторсии конструкции, состоящей из нескольких (например, k ) конечных элементов, удобно записывать в матричной форме:

• [ F ] = [ L ] [ q ] + [ I 1 ].                                              (2)

В этом выражении [ F ] – это столбец, содержащий координаты тензоров дисторсии элементов, перечисленные последовательно в виде блоков

[ F ] = [[ F 1 F 2 F 3 F 4 ] 1 [ F 1 F 2 F 3 F 4 ] 2 … [ F 1 F 2 F 3 F 4 ] k ]^T;

• [ I 1 ]    – столбец, содержащий блоки координат единичного тензора

• [ I 1 ]    = [[1 0 0 1] [1 0 0 1] … [1 0 0 1]]^T;

а [ q ] – столбец, содержащий смещения узлов конструкции

[q] = [q1 q2 … qm]T, где число m – степень свободы конструкции. Матрица [L] размерностью 4k×m определяет связь между смещениями [q] и дисторсией [F]; для каждой конструкции [L] постоянна и ее координаты не зависят от нагрузок или смещений.

Тензор дисторсии представляет скалярное произведение тензора жесткого поворота R и тензоров упругого U e и неупругого U p растяжения:

F = R ⋅ U e ⋅ U p , U e = I + ε e , U p = I + ε p ,                           (3)

здесь тензоры ε e и ε p – это тензоры упругой и неупругой деформации соответственно, а I – единичный тензор. В матричной форме тензоры U e , U p , ε e и ε p записываются в виде столбцов (по аналогии с дисторсией) с учетом симметрии. Например [ ε_e ] – это столбец размерностью 3 k , который содержит компоненты тензоров упругих деформаций ( ε 1 и ε 3 – продольные деформации, ε 2 – сдвиговая) k элементов конструкции:

[ ε ] = [[ ε 1 ε 2 ε 3 ] 1 [ ε 1 ε 2 ε 3 ] 2 … [ ε 1 ε 2 ε 3 ] k ]^T.

Тензор R определяется единственным параметром – углом жесткого поворота ϕ , отложенным против часовой стрелки

R = (e1e1+e2e2) cosϕ + (e2e1–e1e2) sinϕ, а угол ϕ при известном тензоре F и, например, Up определяется следующим образом:

ϕ = arctg[( F 3 U p 3 – F 4 U p 2 +F 1 U p 2 – F 2 U p 1 ) / ( F 1 U p 3 – F 2 U p 2 +F 3 U p 2 – F 4 U p 1 )].

Тензор упругой деформации, который понадобится позже для расчета напряжений и усилий, согласно выражениям (3) имеет вид

ε e = U e – I = R ^T ⋅ F ⋅ U p ^–1 – I .

Для конструкции это выражение записывается в матричной форме:

[ ε e ] = [ B ] [ F ] – [ I 2 ].                                              (4)

Здесь матрица [ B ] размерностью 3 k ×4 k определяет связь между дисторсией и упругими деформациями конструкции в зависимости от смещений ее узлов и накопленной пластической деформации, а столбец [ I 2 ] содержит координаты единичного тензора и имеет размерность 3 k :

• [ I 2 ]    = [[1 0 1] [1 0 1] … [1 0 1]]^T.

Свойства материала описываются моделью идеальной пластичности. Согласно этой модели при упругом деформировании интенсивность напряжений σ i (длина вектора напряжений в девиа-торном пространстве) меньше радиуса поверхности текучести R σ (найденного по пределу текучести при растяжении σ T и, следовательно, равного величине 2/3 σ T ), а при пластическом деформировании σ _i = R _σ ; при этом упругие деформации связаны с напряжениями законом Гука:

σ = С ⋅⋅ ε e , где C – тензор констант упругости. Для конструкции закон Гука приобретает матричный вид

[ σ ] = [ С ] [ ε e ],                                                     (5)

где столбец [ σ ] размерностью 3 k содержит компоненты тензоров напряжений Коши ( σ ₁ и σ ₃ – нормальные напряжения, σ ₂ – касательное) элементов конструкции:

[σ] = [[σ1 σ2 σ3]1 [σ1 σ2 σ3]2 … [σ1 σ2 σ3]k]T, а матрица [С] размерностью 3k×3k содержит константы упругости материала (E – модуль упругости и µ – коэффициент Пуассона).

Плоская конструкция, состоящая из набора треугольных элементов, может быть представлена в виде наложенного на нее «корсета» – фермы, стержни которой шарнирно связанны в узлах и определяют сетку конечных элементов. Они могут растягиваться или сжиматься, но не могут изгибаться, что обеспечивает однородность напряженно-деформированного состояния элементов. Тензор напряжений элемента с помощью граничных условий позволяет найти распределенные силы, действующие на его сторонах, а наличие корсета – заменить систему этих распределенных сил сосредоточенными силами, приложенными к узлам корсета. Для произвольной плоской конструкции выражение, связывающее напряжения элементов и узловые силы имеет следующий вид:

[ Q ] = [ H ][ σ ],                                               (6)

где столбец [ Q ] содержит координаты сил, приложенных к узлам конструкции:

[ Q ] = [ Q 1 Q 2 … Q m ]^T

(по аналогии со смещениями [ q ]), а матрица [ H ] связывает координаты тензоров напряжений элементов конструкции с координатами сил, приложенных к узлам конструкции в ее деформированном состоянии. Очевидно, что матрица [ H ] зависит от смещений, так как равновесие элемента рассматривается в деформированном состоянии.

Щербакова А.О.                         Расчет деформирования геометрически нелинейной плоской конструкции из идеально пластичного материала

При кинематическом нагружении конструкции (то есть при известных смещениях узлов) расчет ведется шагами по времени, при этом на каждом шаге используются пластические деформации, найденные на предыдущем шаге расчета.

Схема расчета при кинематическом нагружении

• 1.    Номер шага нагружения n = 1.

• 2.    Начальные пластические растяжения [ U p *] = [ I ₂].

• 3.    Смещения на текущем шаге [ q _n].

• 4.    Функция уточнения пластических растяжений: [ U p _n] = fq _n, U p *):

• a.    Дисторсии [ F ] = [ L ][ q n ]+ [ 1 1 ];

• b.    Приближенные упругие деформации и напряжения:

[ 8 e *] = [ B ( q , U p *)][ F ] - [ 1 2 ],     [ a *] = [ C ][ 8 e *];

• c.    Приближенный вектор напряжения [ s ] в девиаторном пространстве и его модуль о* (интенсивность напряжений). Для конечного элемента с координатами тензора напряжений о 1 *, о ₂* и о ₃* получим

s 1 =^( о 1 *+ о 3 *),       s 2 =^( о 1 * -о 3 *),       s ; у2 о 2 *,      О / * = ( S 12 + S 22 + S 32 ) '/ ²;

V 6                 V2

• d.    Если в каком-либо элементе конструкции о * >  R _m тогда укорачиваем вектор s до размера R _m затем уточняем координаты тензора напряжений о ;

• е.    Координаты тензоров упругих растяжений

[ U e ] = [ C ] ^- 1 [ о ] + [ 1 2 ];

• f.    Координаты тензоров пластических растяжений

[ U pn ] = [ D ( q n , U e )][ F ]

(здесь матрица [ D ] выражает связь между пластическими растяжениями и дисторсией элементов конструкции);

• g.    Если о_/ * <  R _m тогда не меняем координаты тензоров пластических растяжений [ U p n ] = [ U p *].

• 5.    Координаты тензоров пластических растяжений после поворота элемента как жесткого целого [ V_{p n}]. Например, для одного элемента

• 6.    Координаты тензоров упругих растяжений после поворота элемента как жесткого целого [ V e n ] = [ B ( q n , V p n )] [ F ].

• 7.    Вычисляем напряжения [ о _n] = [ C ] ([ V e _n] - [ 1 ₂]).

• 8.    [ Q n ] = [ H ( q n )] [ о n ].

• 9.    [ U p *]= [ U p _n], n = n + 1, возвращаемся к п. 3.

[ V pn ] = [ R n ] T [ U p n ] [ R n ]

Расчет силового нагружения конструкции также ведется шагами по времени, при этом приходится использовать численные методы решения системы нелинейных уравнений

[ q ] = [ K] ^-1 ([ Q ] — [ b ]), где

• [ K ] = [ H ] [ C [ B ][ L ], [ b ] = [ H ] [ C ]([ B ][ 1 1 ] — [ 1 2 ]).

Верификация модели

C целью верификации предложенной расчетной модели в работе были сопоставлены величины изгибающих моментов M* , возникающих в прямоугольной балке при ее чистом изгибе, вычисленные с помощью предложенной модели, а также моменты

M 1 = Eh ³/(12 р ), M 2 = ( о т h ³ / 4) - о т ³ р²/(3 E ²), вычисленные с использованием точных решений, известных из курса сопротивления материалов. Здесь M । - это момент, вычисленный при упругом деформировании балки, а M ₂ - за пределами упругости, E - модуль упругости материала, р - радиус кривизны балки, h - высота балки. В расчетах использовали следующие исходные данные: материал балки - изотропный, идеально пластичный ( E = 2 - 10⁵ МПа, о _т = 10 ГПа, коэффициент Пуассона р для простоты принят равным нулю), h = 8 м, длина балки l = 15 м, толщина балки равна 1 м, напряженное состояние - плоское, высота конечного элемента - 0,5 м.

На рис. 1 приведена схема балки в начальном состоянии (с разбивкой на конечные элементы) и в конечном, а на рис. 2 показаны зависимости изгибающих моментов от а - угла поворота пра- вого торца балки. Расчет показал, что отличие между предложенным решением и соответствующим точным решением не превышает 1 %.

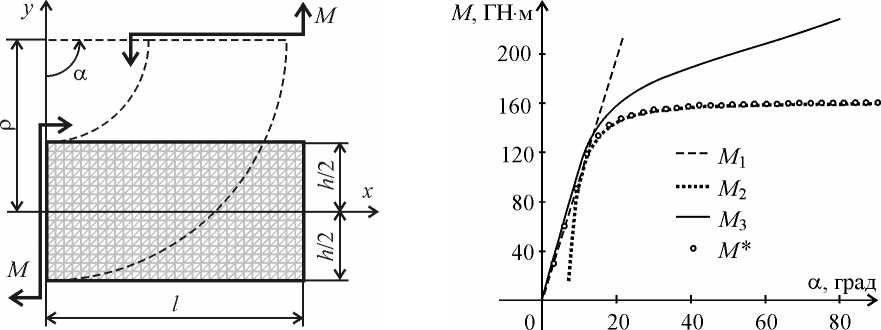
Рис. 2. Зависимости изгибающих моментов от угла α

Рис. 1. Схема чистого изгиба балки при µ = 0                     M 1 и M 2 – точные решения;

M * – решение с помощью предложенной модели;

M 3 – решение с помощью пакета ANSYS

Для сравнения на рис. 2 показано изменение изгибающего момента M 3 , возникающего при чистом изгибе балки, вычисленное с помощью пакета прикладных программ ANSYS (в расчете использовали квадратные элементы plane182 соответствующего размера). Геометрические параметры конструкции и свойства материала использовали те же, что и в расчете с помощью предложенной модели. Расчет показал не только количественное, но и качественное различие между решением рассмотренной задачи в пакете ANSYS и точным решением: с увеличением α значение момента M 3 не стабилизируется на величине 16∙10¹⁰ Нм, а продолжает расти. Это объясняется использованием в пакете ANSYS тензора логарифмической деформации, который при повороте главных осей конечных элементов в результате деформирования, теряет физический смысл [6–8].

Заключение

Предложена расчетная модель позволяющая, зная нагрузки, приложенные к плоской конструкции из идеально пластичного материала, найти соответствующие смещения ее точек и, наоборот, по заданным смещениям найти приложенные к конструкции силы. Модель включает в себя геометрические, статические и физические соотношения и основывается на методе конечных элементов. В качестве меры напряжений используется тензор напряжений Коши, а меру деформаций представляет тензор инженерной деформации.

Для верификации предложенной модели выполнен расчет деформирования балки при чистом изгибе. Сопоставление результатов расчета с соответствующим точным решением, известным из курса сопротивления материалов, позволяет сделать вывод об адекватности предложенной модели (различие между величинами изгибающих моментов, полученными двумя методами, составляет не более 1 %).