Расчет диаметра ходового винта, предназначенного для перемещения робота в теплице

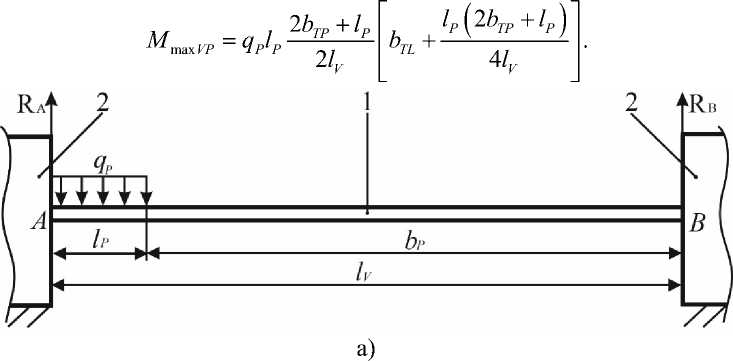
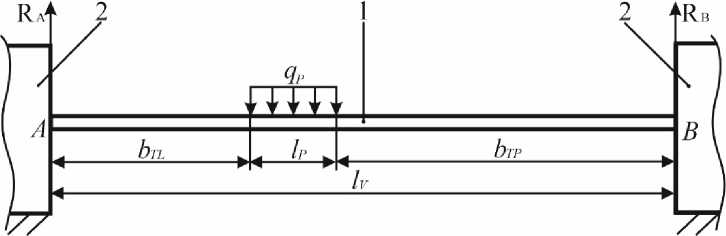
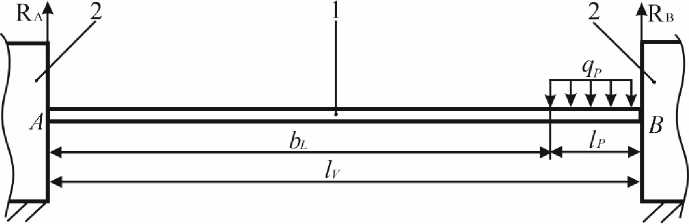
Результаты и обсуждение. В практических условиях при поперечном движении автономного робота по территории теплицы, он может принимать следующие три основные позиции. Первая – левое положение, когда подвижная платформа находится в крайней левой точке относительно продольной оси теплицы, где расстояние от правой стороны левой опорной тележки до левой стороны подвижной платформы оставляет 0 м, а расстояние от левой стороны правой опорной тележки до правой стороны подвижной платформы оставляет bP м. Вторая – текущее положение, когда расстояние от правой стороны левой опорной тележки до левой стороны подвижной платформы оставляет bTL м, а расстояние от левой стороны правой опорной тележки до правой стороны подвижной платформы соответствует bTP м. Третья – это правое положение, когда подвижная платформа находится в крайней правой точке относительно продольной оси теплицы, где расстояние от левой стороны правой опорной тележки до правой стороны подвижной платформы оставляет 0 м, а расстояние от правой стороны левой опорной тележки до левой стороны подвижной платформы равно bL м. На основании сказанного построены схемы нагрузки ходового винта от действия поперечной силы для каждой позиции, которые представлены на рисунке 1, где точка А – точка опоры ходового винта на левую опорную тележку, а точка В – точка опоры ходового винта на правую тележку; RA и RB – реакции опор соответственно в точках А и В. При этом подвижная платформа длиной lP (м) создает погонную нагрузку qP (Н/м) на ходовой винт, длина которого составляет lV , м.

приведенным в ходового винта

Для схемы, изображенной на рисунке 1а, согласно рекомендациям, источнике [12], максимальный изгибающий момент в поперечном сечении составит

M

_ q p l p

max PP 8

2 -к

l

l

P

V 7

В отношении схемы, изображенной на рисунке 1б, с учетом

рекомендаций,

представленных в источнике [12], максимальный изгибающий момент в поперечном сечении ходового винта будет равен

б)

в)

1 – ходовой винт; 2 – опорная тележка а – первая позиция; б – вторая позиция; в – третья позиция

Рисунок 1 – Схемы нагружения ходового винта

При этом согласно схеме, изображенной на рисунке 1в, с учетом рекомендаций [12], максимальный изгибающий момент в поперечном сечении ходового винта определяется выражением

M max TP

_ q P l P

V

—

т

lv 7

Так как M max _PP _ M max TP , то обуславливаемся, что итоговый максимальный изгибающий момент в поперечном сечении ходового винта для первой и третьей позиций робота в теплице соответствует следующему равенству

М = М = М

max IP max PP max TP ^.

В зависимостях (2), (3) и (4) погонная нагрузка, действующая на ходовой винт, рассчитывается по формуле

( m PP + m Tz + m oz ) g  m R g

qP _--------7--------_ —,

где g – ускорение свободного падения, м/с ² ;

m_PP – масса подвижной платформы, кг;

m_TZ – масса телескопической штанги с захватывающим устройством, кг;

m_OS – масса объекта захвата, кг;

m_R – расчетная масса, кг.

Согласно описанию роботизированной теплицы, представленному в работах [3, 4], подвижная платформа опирается на ходовой винт и на ограничитель. Отсюда следует, что суммарная масса подвижной платформы, телескопической штанги с захватывающим устройством и объекта захвата полностью не воздействует на ходовой винт, так как определенную часть воспринимает ограничитель. Долевое распределение воздействия

Агротехника и энергообеспечение. – 2025. – № 4 (49)                        239

указанной массы на ходовой вин зависит от ряда факторов, основными из которых являются способ крепления телескопической штанги к подвижной платформе и расстояние между центрами ходового винта и ограничителя.

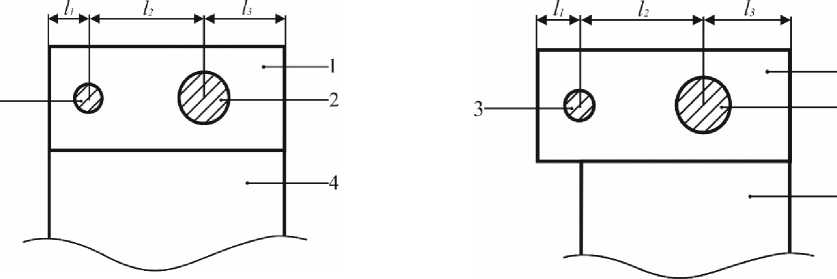
На рисунке 2 показано наиболее рациональное крепление телескопической штанги к подвижной платформе.

а)                                                      б)

1 – подвижная платформа; 2 – ходовой винт; 3 – ограничитель;

4 – телескопическая штанга а – на всю ширину подвижной платформы;

б – частичное перекрытие ширины подвижной платформы

Рисунок 2 – Схемы крепления телескопической штанги к подвижной платформе

В соответствии со схемой, изображенной на рисунке 2а, расчетная масса, воздействующая на ходовой винт, составит m„ = (mP p + m-г7 + m^?) R      PP TZ OZ

0,5 1 2 + 1 з

1 1 + 1 2 + 1 3

где l ₁ – расстояние от ближнего края подвижной платформы до центра ограничителя,

м;

l ₂ – расстояние между центрами ограничителя и ходового винта, м;

l ₃ – расстояние от ближнего края подвижной платформы до центра ходового винта, м.

Для схемы, приведенной на рисунке 2б, расчетная масса, воздействующая на ходовой винт, определяется следующим образом mR = mpp

0,5 1 ₂ + 1 3

^l 1 ^{+ 1} 2 ^{+ 1} 3

+ ( mTZ + mO)Z )

0,5 1 ₂ + 1 3

¹ 2 ^{+ 1} 3

В равенстве (1) M СХВ = M max ip при условии M max ip >  M m _a x vp , еСли M max ip <  M m _a x vp , То

M СХВ = M max Vp ^.

Крутящий момент в сечении ходового винта, с учетом рекомендаций [11], определяется из выражения

M_KX b= — ,                          (9)

КХВ

^SD где NSD – мощность серводвигателя, Вт;

a _SD — угловая скорость серводвигателя, рад/с.

Учитывая равенство (1) и применив методику обоснования параметров специального пути для перемещения робота в теплице [4], запишем конечную формулу для расчета минимально допустимого диаметра ходового винта dminХВ

V

^{32 [} k ЗИХВ ] ^M тахПХВ

^П& ихв k пихв

где п - число «пи», постоянная величина примерно равная 3,14;

[ k зихв ] — коэффициент запаса прочности при изгибе и кручении ходового винта, равный 2,0…3,0 [4, 8, 9];

• а _ихв — предельно допустимое напряжение при изгибе ходового винта, Па;

k _ПИХВ – коэффициент понижения расчетного напряжения при возникновении неравномерности распределения нагрузок в ходовом винте и из-за наличия в нем резьбы, равный 0,8 [4].

Вывод. Разработанная методика обоснования параметров ходового винта позволит точно рассчитать минимально допустимый его диаметр, так как учитывает одновременное воздействие изгибающего и крутящего моментов, что дает возможность обеспечить надежное перемещение автономного робота по территории теплицы при выполнении установленных функций.