Расчет динамики баллистической модели ракет

При разработке перспективных морских ракетных комплексов нашел широкое применение метод баллистических испытаний моделей в специализированных гидродинамических бассейнах. Его применение позволяет на ранних стадиях проектирования выбирать наиболее оптимальные при заданных ограничениях гидродинамические схемы старта, ракет [1]. Для обеспечения безопасности испытаний и сохранения многоразового использования модели применяют различные системы улавливания и торможения модели. Наиболее надежными и безопасными из них зарекомендовали себя гидравлические системы, в которых модель по направляющим входит и тормозится в заполненной водой цилиндрической трубе с глухим днищем [2]. Однако разработка метода, их расчета остается до сих пор актуальной. В статье разрабатывается математическая модель и метод расчета динамики баллистической модели в гидравлическом улавливающем устройстве, которые позволяют выбирать его геометрические параметры и проводить торможение модели в заранее заданном расчетном режиме, что позволяет снизить перегрузку модели и возникающее избыточное давление жидкости в трубе [3]. Области знаний, связанные с исследованием динамики баллистических моделей ракет, расчетно-теоретическим и экспериментальным исследованиям подводного старта, а. также сопутствующие им процессы с нестационарными двухфазными потоками с учетом тепломассобмена, является в настоящее время актуальными, и им посвящены работы многих авторов [4-8].

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

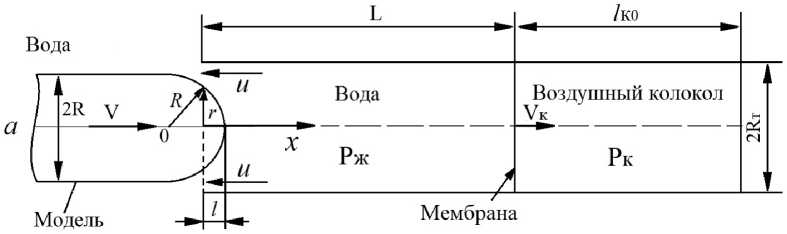
На рис. 1 приведена схема гидравлического улавливающего устройства, которое состоит из цилиндрической трубы с глухим днищем. Модель начинает тормозиться при входе носка модели в трубу (рис. 1 а), более интенсивное торможение происходит после входа носка модели в трубу (рис. 1 б). С целью смягчения процесса торможения, а также ликвидации возможных явлений гидроудара (пиков давления в жидкости и перегрузок модели) в торце трубы дополнительно предусматривается воздушный колокол, загерметизированный эластичной или легкоразрушаемой мембраной. При возникновении избыточного давления в жидкости мембрана смещается к торцу, давление в объеме колокола при этом возрастает. При входе носка модели в затопленную трубу между моделью и трубой образуется кольцевой зазор, через который вода начинает вытесняться из трубы. Модель обычно представляет собой вытянутое тело вращения с цилиндрическим корпусом, заканчивающимся плоским срезом, а профилированная форма носка близка к сферической.

Воздушный

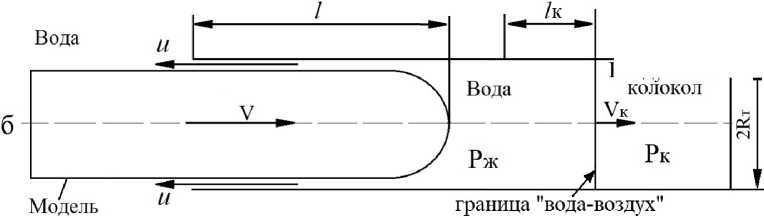
Рис. 1. Схемы улавливающего гидравлического устройства: а - вход носка модели, б - движение в трубе

Площадь поперечного сечения кольцевого зазора при входе сферического носка в трубу зависит от координаты его сечения x

Sk з = п ( x ² — 2 Rx + RT )    пpn l < R.

После входа носка в трубу площадь кольцевого зазора становится постоянной и определяется равенством

S _K.з = п ( RT — R 2 )    при l > R.                       (2)

Здесь l - путь, пройденный моделью, R, RT - радиусы модели и трубы.

Для определения скорости границы VK используем интеграл Коши - Лагранжа для течения жидкости в трубе дф VI Pk = Pk at + 2 + р р 1

В.И. Пегов, И.Ю. Мошкин

где ф = xVK - потенциал скороети течения в трубе, VK = дф/дх - скорость жидкости, PK - давление в воздушном колоколе. Р ж ~ давление жидкости в трубе, p - плотность жидкости. Из интеграла Коши - Лагранжа найдем дифференциальное уравнение для

скорости границы

^dVK _ P I< — PK   VK

- dt       pxK     2 xK ’

где xK = L — l + l_K . Дифференциальное уравнeiiiie перемещения границы l_K

= V k • ∂t

Начальные условия при t = 0 для уравнения (4) VK = 0, для уравнения (5) 1K = 0. В адиабатическом приближении выражение для давления в объеме колокола примет

вид

PK = PK 0

PK 0  )

l_{K 0} - l_K

где PK 0 , PK - начальное и текущее давлеиия в воздушном колоколе. 1K 0 - начальная длина воздушного колокола, к = 1 , 4 - показатель адиабаты для воздуха.

Составляющая кинетической энергии течения воды в трубе, вызванное скоростью мембраны, запишется в виде

TK = ^ K ST ( L ^— l + lK ) ,

где ST - площадь сечення трубы ST = nRT . L - начальная координата, х границы колокола, l - путь, пройденный моделью.

Дифференциальные уравнения продольного движения модели получим исходя из закона количества движения, представленного в виде уравнения Лагранжа [1]

d ∂T Σ dt ∂V

Здесь производная по времени d берется в подвижной системе координат, Т ^ - суммарная кинетическая энергия, V - продольная скорость модели в направлении OX, F - главный вектор всех сил, приложенных к модели, кроме уже учитываемых в уравнении Лагранжа сил воздействия невязкой жидкости.

Исходя из представленной на рис. 1 схемы, значение Т ^ представим в виде суммы

T _s = ( M + А ) V ² + Т_К з+ T k ,

где M - масса, модели. А - присоединенная масса, модели в жидкости. Т^з - составляющая вызываемого течения воды в кольцевом зазоре, TK - составляющая, обусловленная движением границы раздела « воздух-вода » воздушного колокола, рассчитываемая по формуле (7). Исходя из известных зависимостей присоединенных масс сферы (А с ф = 3 npR ³) и ди ска ( А = 3 pR ³), приближенное выражение присоединенной массы модели, состоящей из цилиндрического корпуса, заканчивающегося сзади плоским срезом а, спереди сферическим носком, запишем в виде

^А = 3 PR ³ + 3 PR 3 = ^П у^ PR ³ • (Ю)

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Входящая в (8) сила F, связанная со свойствами вязкости жидкости, определяется как сила вязкого трения модели с коэффициентом Cxf

F =

-Cxf

_S ρu ²

S 2 ^,

(П)

где S = nR ² - площадь миделя модели. Однако из-за малой величины этой силы далее будем полагать ее равной нулю ( F = 0).

Скорость вытесняемой через кольцевой зазор воды и в соответствии с уравнением неразрывности и равенствами (1), (2) определяется в сечении кольцевого зазора с координатой x выражениями u=

V (2 Rx - x 2) - V k RT

( x ² - 2 Rx + RT )

VR ² - VKR_T ²

= RT - RR

при l < R, при l > R.

Для определения Ткз запишем приращение присоединенной массы dm в сечении кольцевого зазора dm = pS^dx.

В соответствии с этим приращение кинетической энергии dT^3 представим в виде dTK 3 = Р^- SK3dx

II Ткз найдем как интеграл по пути модели l т - Р f l 2 Q д - PV2 т TK 3 = 2 J u SK idx = “У J, где J = I V2SK>dx.

После проведения интегрирования с учетом формул для скорости и (12) и + кз (1), (2), получим при входе носка модели в трубу ( l < R ) и при последующем движении модели в трубе ( l > R )

J i (l ) = п {l ( l ² / 3 - Rl + R 2_T ) + 2 lRT V k +

(1 - Vk)2R4         l - R            R M при l < R.

l > R.

+-- .        - arctg — .        : + arctg

R_T ² - R ²          R ² _T - R ²          R ² _T - R ²

R ² - VкRT) 2_/7

J 2⁽ l ) = J 1^{( R} ) + ^п    _R 2 _{- R} 2   ⁽ l ^{- R} )    при

Здесь VK = VK/V. J 1( R ) определяется из выражения для J 1 ( l ) nj>11 l = R. то есть

J i( R ) = n^RRT (1 + 2 Vк )

-

+

(1 - V k )² RT         R

VRT - R ^{2 arcts} V RT - R ²

В.И. Пегов, И.Ю. Мошкин

В результате выражение для суммарной кинетической энергии с учетом формул (9), (10), (13) - (15) примет вид

T s( ^l ) ^— 2^^ММ + А + p^J i( l )) + ^^ KST ⁽ L — l + lK )    при l < R,

T s( l ) — ~( М + А + pJ 1( l ) + pJ 2( l )) + Р 2 K S t ( L - l + I k )    ^п 1^>п l > R.

На основании уравнения Лагранжа (8) и полученных выражений для T Д l ) найдем основные дифференциальные уравнения для скорости движения модели V:

• -    при входе носка модели в трубу:

dV —__1________________ ( V2 (2Rl - l2 - VkRT)2 \     (l < dt     М + А + pJi(l)+ pVSt (L — l + Ik) ПР     l2 - 2Rl + RT J npn -

• -    при движении модели в трубе:

dV —______________ (.„V2 (R2 - VKRT>2   . l > R dt     М+А+pJi(R)+pJ2(l)+ pVSt(L-I+Ik)   P     RT - R2 )

Для замыкания системы добавим дифференциальное уравнение для пути модели dl — V , а также уравнения (4), (5) для перемещения границы колокола и выражения для давления жидкости в трубе

^Рл < ^{— Р} ж о +

pV2 (2Rl - l2 - VkRT)2 l2 - 2 Rl + RT при l < R,

P i < ^{— Р} ж о +

pV ² ( R ² - V k RT )²

R T - R ²

при l < R,

где Р жо ~ начальное давление в трубе.

Разработанная математическая модель реализована в виде программы на ЭВМ. Интегрирование системы дифференциальных уравнений проводилось при этом методом Рунге - Кутты четвертого порядка точности. Результаты расчетов удобно представить в безразмерном виде. Связь между начальной скоростью модели V и начальным давлением в жидкости Р жо выражается числом Эйлера Eu — Ржо/ ( pV₀ 2). Затем введем следующие безразмерные параметры: времени t — tV 0 /D ( D — 2 R ), массы модели М — М / ( pD 3), скорост и модели V — V/V ₀, площади кольцевого зазора 5 — ( D_T/D )² - 1. г,те D_T — 2 R_T начальной длины всэздушиого колокола, l_K о — l_K о /D и длины объема, заполненного жидкостью L — L/D. Для опорного варианта расчета приняты следующие численные значения: М — 10, Eu — 0 , 67, 5 — 0 , 27, L — 7, l_K о — 3 и t — 52 1 . Результаты расчетов представлены в виде графиков зависимостей 1 7. I³к- Р-ж <>т С г.те Р^ж — Р ж / ( pV^Y I³к — Рк/ ( pV )²).

На рис. 2-4 проводится сравнение расчетов с экспериментальными данными, полученными при испытаниях в гидробассейне. Наблюдается удовлетворительное со ответствие расчетных и экспериментальных данных, что служит подтверждением достоверности и надежности разработанной математической модели тормозного гидродинамического устройства.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

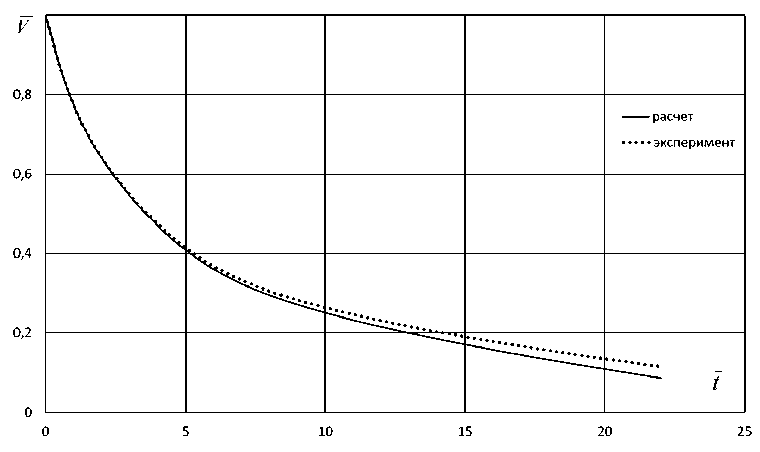
Рис. 2. Сравнение расчетных и экспериментальных значений безразмерной скорости модели V

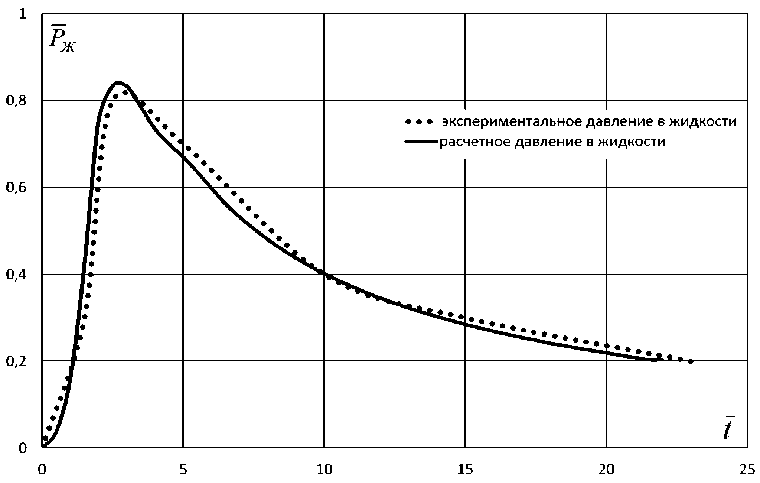
Рис. 3. Сравнение расчетных и экспериментальных коэффициентов давления Рж

Разработанная математическая модель позволяет при заданном числе Эйлера и заданной массе модели выбирать необходимые для торможения основные параметры улавливающего тормозного устройства ( 5, L, 1K о) и найдет использование при экспериментальной отработке подводного старта ракет.

Работа выполнена при поддержке гранта 14-08-00128 Российского фонда фундаментальных исследований.

В.И. Пегов, И.Ю. Мошкин

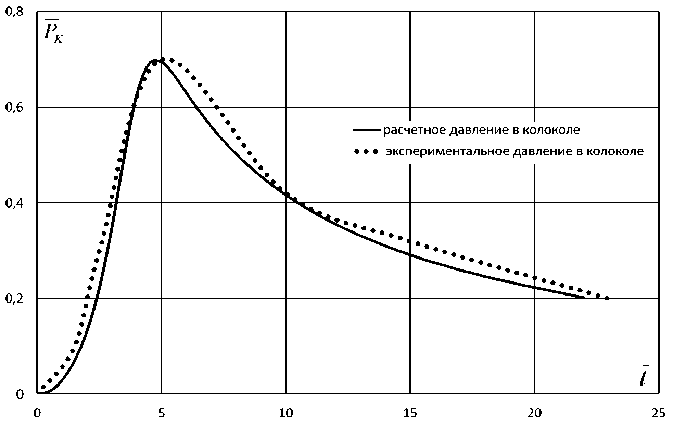
Рис. 4. Сравнение расчетных и экспериментальных коэффициентов давления PK