Расчет двухкаскадной длиннопериодной волоконной решетки показателя преломления

За последние несколько десятилетий волоконные структуры со вставками специальных волокон благодаря их особым характеристикам получили широкое распространение в волоконно-оптической технике [1]. Среди них наиболее применимыми являются длиннопериодные волоконные решетки (ДПВР), представляющие собой отрезки одномодовых волоконных световодов (ВС) с периодически изменяющимся показателем преломления (ПП) сердцевины с периодом порядка 100– 500 мкм. ДПВР находят применение в системах измерения различных физических величин из-за своих уникальных характеристик, таких как возможность дистанционного измерения, высокой чувствительности, небольших габаритных размеров, высокой точности, способности одновременного измерения нескольких параметров, высокого быстродействия и устойчивости к электромагнитным помехам [2; 3].

Для теоретического исследования данных структур необходим высокоэффективный и теоретически обоснованный метод, который позволит произвести расчет их спектральных характеристик.

Для расчета ДПВР в настоящее время применяют метод, основанный на решении системы уравнений связанных волн [4]. Однако данный метод применим только для расчета однородных решеток с достаточно большим числом периодов.

Неоднородные (с изменяющимися по длине параметрами) ДПВР могут быть строго рассчитаны с использованием метода частичных областей [5], в основе которого лежит решение задачи дифракции основной волны ВС на неоднородностях показателя преломления или формы сердцевины волокна. Данная математическая модель характеризуется большой размерностью, которая при решении задач анализа и синтеза приводит к сложностям в вычислении. Для решения этой проблемы возможно использование метода декомпозиции, т. е. разбиения исходной сложной системы на подсистемы меньшей размерности [5; 6]. Таким образом, в основе предлагаемой в настоящей статье методики расчета ДПВР лежит решение задачи дифракции основной волны ВС на неоднородностях в виде ступенчатого изменения показателя преломления сердцевины. Целью данной работы является построение алгоритма и расчет каскадных ДПВР.

1.    Электродинамическая модель

Расчет каскадных ДПВР строится на основе строгой электродинамической модели базовой неоднородности трехслойного волоконного световода. Схематично структура изображена на рис. 1.

Рассмотрим задачу дифракции основной волны HE ₁₁ в данной структуре. Для упрощения расчетов будем считать, что каждый стык волокон есть

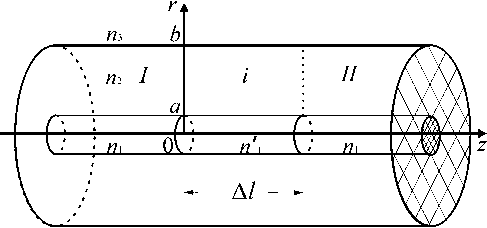
Рис. 1. Базовая неоднородность

Fig. 1. Basic heterogeneity

N z i.

-YF(i ’(E^ i’ • + E( i’ •• kie n A Li X Fn ’Ern r0 + ESn S0)e n=1                                          .

N

_ X ¹ r\ ’ i ^{+ 1)}     ’ i ^{+ 1) —} •        ⁽ i ^{+ 1) —}

= X Dn   ’Ern  'r0 + ESn  'S0’ - n=1

S i

N

E P ⁽ i ^{+ 1)}/l7 ( i ^{+ 1) —} • I p( i ^{+ 1) —} \

F n   ⁽ E rn   * ^r 0 ⁺ E S n  '^S 0⁾

n =1

S i

N

E P) ⁽ i ^{)    (} i ^{) —        (} i ^{)   —}       i ^e n ^ ^L i

D n ⁽ H rn ' ^r 0 ⁺ H S n ' ^S 0^{) e +} n =1

соединение регулярных отрезков волноводов, параметры которых постоянны. Пусть на структуру слева падает основная волна единичной амплитуды йЕц . В каждом отрезке волновода поле представляет собой набор отраженных и прошедших волн.

Поле дифракции в волноводе I является суперпозицией падающей волны HE ₁₁ и бесконечного количества отраженных собственных волн:

N                                        ..( i _)1T

I X ¹ p ( i ^{)    (} i ^{) —        (} i ^{) —}     Ф n ^ ^L i

+ X Fn (Hrn*r0 + H Sn *S0)e n=1

S i

N

_ X ¹    ( i ^{+ 1)}     ( i ^{+ 1) —} •        ⁽ i ^{+ 1) —}

= X Dn  (Hrn  'ro + HSn "S0) + n=1

N

■ X ¹ p ( i⁺¹)(рг⁽i ^{+ 1) —} • Lj( i ^{+ 1) —} \ ⁺ X F n ⁽ H rn 'r o ⁺ H S n "^S 0)

n =1

' e ⁽ I ’ ' й ⁽ I ’"

' E 1 I ’ й 1 I ’

Г e

^I ’ z

+

to

X Cn \ n=1

^— ( I ) ^E - n

——

H

( I )

- n

> ei^I ’ z ,

где i = 0,1,2,..., K -1;

S i

поле в волноводе i – суперпозиция бесконечного набора прошедших и отраженных собственных

D (0) = I ¹ , ^П Р ^{И n} = ^{1 n} 1 0, при n ^ 1;

волн:

E — ’*’

H

= X D ni i

n =1

to

+

X Fn¹ ’

n =1

p ⁽ i ’ E _{- n}

—

H

- ( i )

- n

p ⁽ i ’

En

H nii

Г e

.-Ф^ z

+

. X z ,

в волноводе II поле представляется в виде бесконечного набора прошедших собственных волн:

' E ⁽ II ’ H ⁽ II I

= X B n

n =1

6 ( II ) E_n

H ⁽ II ’ n

Г e

.-<" ’ z

,

где C n , D ni ’ , F n¹ ’ , B n - постоянные неизвестные

— ⁽ I ’      /— ’ I ’      — ’ I ’      /— ’ I ’      — ’ i ’      /— ’ i ’

Коэффициенты; E , H , ^E - n , ^H - n , ^E ± n , ^H ± n ,

E nnII ’ , H II ’ - векторные функции, описывающие зависимость поля от поперечных координат; P 1 I ’ , p ⁽ _n I ’ , P ni ) , P ^I ’ — продольные постоянные распространения волн соответствующих волноводов.

Условия непрерывности тангенциальных составляющих электрических и магнитных полей на границе волноводов I и i запишутся в виде:

N

X D n "' E rU + E S 1^0 e -^# n L i -              (4)

n =1

F ⁽⁰⁾ = C

F n     C n .

На границе волноводов i и II граничные усло-

вия записываются в виде:

N

Yd(i)(e(i’ • + e’i) •• k-ip-’ALi X Dn (Ern r0 + ESn S0)e n=1

N i ’_ _     p ⁽ i’(pli ’ .^—₊ J7⁽ i ’ . •) V i P n ^{A L} i

X F n ’ E rn ^r 0 ⁺ E S n ^S 0^{) e}

n =1

M

E r ( II )   ( II ) ^— 4. _F( II )

^Bm ⁽ E rm '^r 0 ⁺ E S m

m =1

N

X D n^{: )}( H rn ' • r 0 + H S' n •S 0 )e

-

Sê

•^S 0⁾     >

S ê

.— i e n ’ A L i +

n =1

N                               i ’_

+ X F ⁽ i ’    ⁽ i ’ • ^{—       (} i ’ • ^— V^е n ^{A L} i

⁺ X F n ⁽ H rn ^r 0 ⁺ H S n ^S 0^{) e}

n =1

M

E r ( II ⁾     ( i ^{+ 1) —}       ( i ^{+ 1)}

Bm (Hrm 'r0 + Hsm m=1

S ê

•^S 0⁾     ,

Sê

где M , N - число учитываемых волн; — 0 , S 0 — единичные векторы цилиндрической системы координат; A L i - значение продольной координаты, соответствующее границе S_i двух волноводов.

В случае дифракции основной волны HE ₁₁ на осесимметричном переходе будут возбуждаться только волны с одной вариацией электромагнитного поля по угловой координате. Поэтому при записи граничных условий (4)–(7) достаточно учесть волны с азимутальным индексом, равным единице.

Векторно умножаем уравнение (4) на ( H r q ⁾ • 1 0 + + H % •ф о ), а (5) - на ( E q ^{+ 1)} • ? о + E ^f •ф о ) и интегрируем получившиеся выражения по поперечному сечению соответствующего волновода S i . Аналогичные операции производим с уравнениями (6)–(7). Используя энергетическую ортогональность собственных волн, получаем систему линейных неоднородных уравнений относительно неизвестных амплитудных коэффициентов волн в матричной записи:

E • C - W ⁽⁰ ) D ⁽¹ - W ⁽⁰ ) ¥ ⁽¹⁾ F ⁽¹⁾ = - I ; (8) - W ⁽⁰ T C - ED ⁽¹⁾ +Т ⁽¹ F ⁽¹⁾ =- I;

^ ⁽ i ) d ⁽ i ) + ef ⁽ i ) - w ⁽ i ) d ⁽ i ^{+ 1)} - w ⁽ i ) ^ ⁽ i ^{+ 1)} f ⁽ i ^{+ 1)} = 0;

W ⁽ i ^)T ^ ( i ) d ⁽ i ) - w ⁽ i ^)T f ⁽ i ) - ed^ i ^{+ 1)} +^ ⁽ i ^{+ 1)} f ⁽ i ^{+ 1)} = 0;

^ ⁽ K ) d ⁽ K ) + ef ⁽ K ) - w ⁽ K ) ^ ⁽ II ) в = 0;

W(K)T^(K)d(K) - w(K)Tf(K) -^'(II)в = 0, где E – единичная матрица с элементами Eq,n =5q,n (sq,n — символ Кронекера); C, D(i), F(i), D – векторы-столбцы неизвестных амплитудных коэффициентов; I – вектор-столбец с элементами I =5 ; I - вектор-столбец с элементами q      q ,0

I q = j ( E rq ) H фо - E s q H r o)ds ;

S

Wⁱ – матрицы с элементами

W in = j ( E rq ^{+ 1)} H 2 - Ei^ H r n) ds ;

S

W^T - транспонированные матрицы; T ⁽ i ) - диагональная матрица, элементы которой ^ П ⁾ _п = = e i ^{e n Л} L i учитывают набег фазы волны с номером n . Здесь всюду i = 0,1,..., K , n = 1,2,..., N , q = = 1,2,..., N , m = 1,2,..., M .

Систему (8) можно также записать в виде матричного уравнения, которое позволяет найти амплитудные коэффициенты C n , B m , D nni ) и F ni ) волн в волноводах I , II и i -й области исследуемой структуры, изображенной на рис. 1. Таким образом матричное уравнение запишется в виде

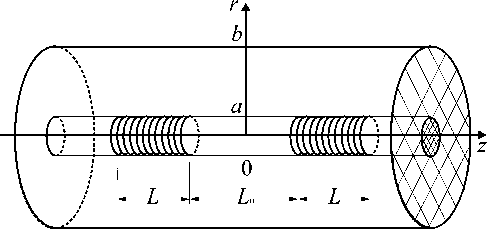
Рис. 2. Двухкаскадная ДПВР

Fig. 2. Two-stage DPVR

S • X	= r ,	(9)
где	" C "		^- ' 1
	D (1)		/*/ - 1
	F (1)		0
X =	D( ii	, r =	0
	F ( i )		0
	B		0

– вектор-столбцы;

	E - W < 0 ) T	- W (0 ) - E	- W (0 ) ^ (1) ^ ( 1)	0 0
S =	0		^ ( i )	E
	0		w ( i )T ^ ( i )    -	W (	: i ) t
	0	0	0		.
	_ 0	0	0		.
	0		00	1
	0		00
- W1	( i )    - w ( i ) ^ ( i + 1)		...            0
- E       T ( i + 1)			...            0		.
0	^ ( K)		•                               • E    - W ( K )
0	W ( K ) T	^ ( K )	- W ( K ) T   - E	.

При расчете структур с большим количеством неоднородностей длиннопериодной волоконной решетки, а также их каскадов предлагаемый метод частичных областей приводит к вычислению матриц большой размерности и, как следствие,

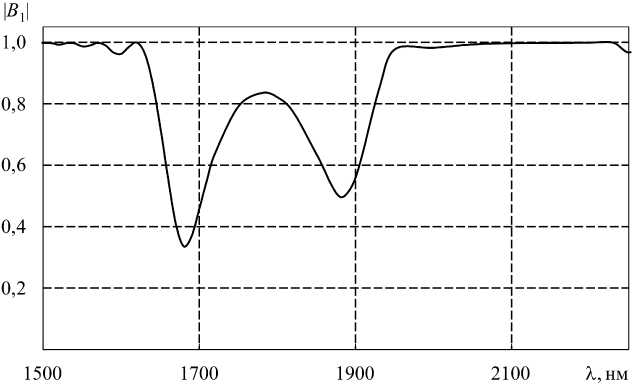
Рис. 3. Спектр пропускания ДПВР с периодом T = 122 мкм, L = 1,9886 см

Fig. 3. Transmission spectrum of the DPVR with a period T = 122 microns, L = 1,9886 cm

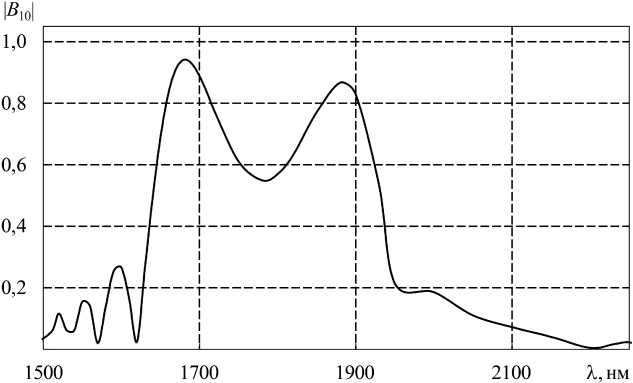
Рис. 4. Спектральная зависимость модуля коэффициента возбуждения волны HE ₁₉ ДПВР с периодом T = 122 мкм, L =1,9886 см

Fig. 4. Spectral dependence of the modulus of the excitation coefficient of the HE ₁₉ wave of the DPVR with a period T = 122 microns, L = 1,9886 cm

к большим вычислительным затратам. Выходом из данной ситуации является применение метода частичных областей в сочетании с методом декомпозиции [7]. В этом случае расчет базовой неоднородности производится методом частичных областей, а затем с помощью метода декомпозиции находятся характеристики всей структуры [8; 9].

2.    Реализация метода на примере расчета каскадной ДПВР

На основе предложенной электродинамической модели был произведен расчет структуры с двухкаскадной ДПВР, изображенной на рис. 2. Для апробации алгоритма расчета исследуемая структура была сведена к ДПВР с параметрами, предложенными в [5]. Результаты расчета, приведенные на рис. 3 и 4, совпали с графической точностью с результатами, представленными в [5]. На рис. 3 показан спектр пропускания, а на рис. 4 – спектральная зависимость модуля коэффициента возбуждения волны HE19.

На рис. 5–7 приведены спектр пропускания каскадной решетки, спектральная зависимость модуля коэффициента возбуждения волны HE ₁₅ и спектральная зависимость модуля коэффициента возбуждения волны HE ₁₈ соответственно при следующих параметрах: период решетки составил T = 750 мкм, длина обеих ДПВР - по L = 3,1125 см, расстояние между решетками (длина вставки одномодового волокна) составила L = 18,746 см. Ра

В диус сердцевины 1,455 мкм, а оболочки – 62,5 мкм. Количество учитываемых волн бралось равным 10.

Из графиков спектра пропускания и спектральных зависимостей модулей коэффициентов возбуждения высших типов волн HE ₁₅ и HE ₁₈

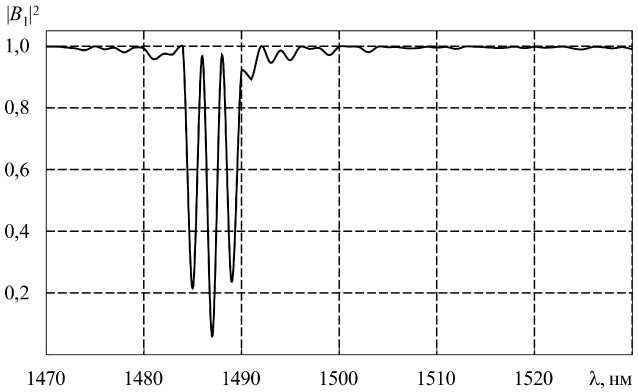
Рис. 5. Спектр пропускания каскадной решетки с параметрами T = 750 мкм, L = 3,1125 см, L _в = 18,746 см

Fig. 5. Transmission spectrum of the cascade array with parameters T = 750 microns, L = 3,1125 cm, L _v = 18,746 cm

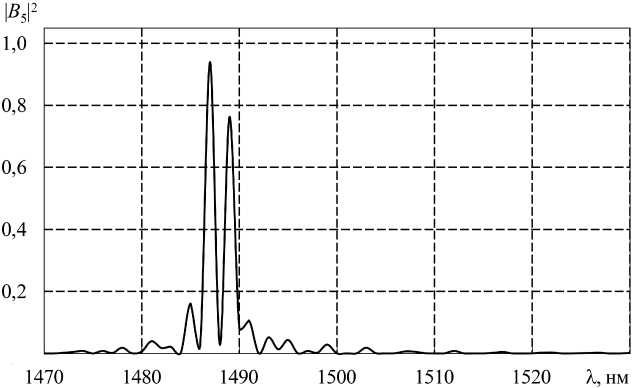
Рис. 6. Спектральная зависимость модуля коэффициента возбуждения волны HE ₁₅ каскадной решетки с параметрами T = 750 мкм, L = 3,1125 см, L _в = 18,746 см

Fig. 6. Spectral dependence of the HE ₁₅ wave excitation coefficient modulus of a cascade array with parameters T = 750 microns, L = 3,1125 cm, L _v = 18,746 cm

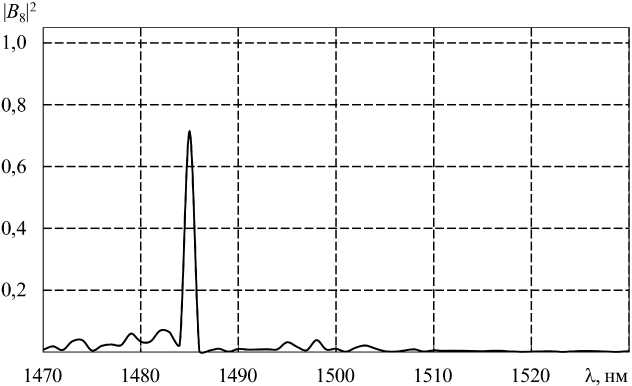
Рис. 7. Спектральная зависимость модуля коэффициента возбуждения волны HE ₁₈ каскадной решетки с параметрами T = 750 мкм, L = 3,1125 см, L _в = 18,746 см

Fig. 7. Spectral dependence of the modulus of the excitation coefficient of a wave of HE ₁₈ cascade array with parameters T = 750 microns, L = 3,1125 cm, L _v = 18,746 cm

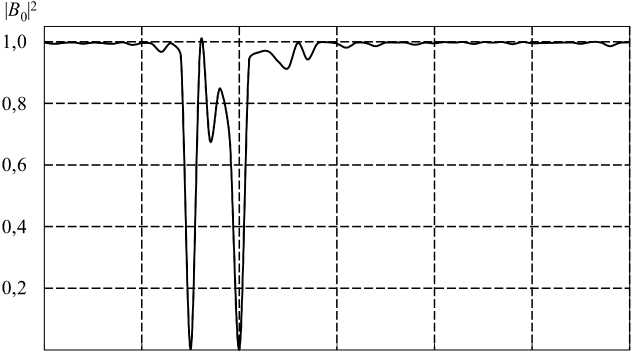
1470      1480      1490      1500      1510      1520 X, нм

Рис. 8. Спектр пропускания каскадной решетки с параметрами: T = 752 мкм, L = 4,1736 см, L _в = 18,756 см

Fig. 8. Transmission spectrum of the cascade array with parameters: T = 752 microns, L = 4,1736 cm, L _v = 18,756 cm

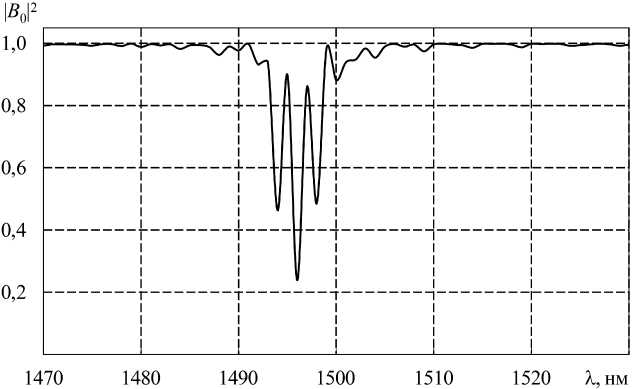
Рис. 9. Спектр пропускания каскадной решетки с параметрами: T = 750 мкм, L = 2,6625 см, L _в = 18,75 см

Fig. 9. Transmission spectrum of the cascade array with parameters: T = 750 microns, L = 2,6625 cm, L _v = 18,75 cm

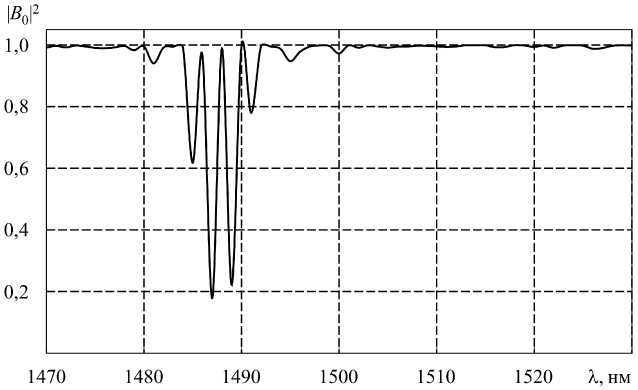
Рис. 10. Спектр пропускания каскадной решетки с параметрами: T = 750 мкм, L = 2,6625 см, L _в = 18,747 см

Fig. 10. Transmission spectrum of cascade grating with parameters: T = 750 microns, L = 2,6625 cm, L v = 18,747 cm

следует, что в диапазоне длин волн от 1470 нм до 1530 нм коэффициент прохождения близок к 1, но на длине волны 1485 нм энергия основной волны HE ₁₁ переходит в энергию оболочечной моды HE ₁₈ (показано на рис. 7), а на длинах волн 1487 нм и 1489 нм переходит в энергию оболочечной моды HE ₁₅ (рис. 6). Спектр пропускания качественно совпадает с результатами из [10].

Спектр пропускания каскадной ДПВР со следующими параметрами: период T = 752 мкм, длина решеток L = 4,1736 см, расстояние между решетками L _в = 18,756 см, радиус сердцевины 1,455 мкм, оболочки - 62,5 мкм, представлен на рис. 8. Количество учитываемых волн бралось равным 10.

Нетрудно видеть, что при данных параметрах коэффициент прохождения по основной волне HE 11 на длинах волн 1485 нм и 1490 нм стал практически равен нулю, но на длине волны 1487 нм увеличился до 0,67.

На рис. 9 представлен спектр пропускания ДПВР, рассчитанной при следующих параметрах: период решетки T = 750 мкм, длина обеих ДПВР L = 2, 6625 см, расстояние между решетками составило LB = 18,75 см, радиус сердцевины 1,455 мкм, а оболочки – 62,5 мкм. Количество учитываемых волн бралось равным 10. А также на рис. 10 при веден спектр пропускания ДПВР с аналогичными параметрами периода решетки и длины обеих ДПВР, но с другим расстоянием между решетками Lв = 18,747 см. Радиус сердцевины и оболочки, а также количество учитываемых волн брались такими же, как и в предыдущих случаях.

Из приведенных графиков видно, что при уменьшении расстояния между решетками спектр пропускания смещается в коротковолновую область.

Заключение

Предложен метод расчета спектральных характеристик каскадных длиннопериодных волоконных решеток показателя преломления сердцевины. Согласно алгоритму, структура представляется в виде каскадного соединения базовых неоднородностей, каждое из которых рассчитывается методом частичных областей. Преимуществом метода является возможность теоретически исследовать влияние на спектральные свойства структуры от диэлектрических и геометрических параметров, а также значительно сэкономить временные ресурсы. Приведены спектры пропускания решеток с различными параметрами периода T , длины решеток L и расстояния между решетками L _в.