Расчет фрикционно-механических характеристик тканых и шовных материалов

В медицине широкое распространение получили разнообразные тканые и шовные материалы на основе натуральных и синтетических волокон. К ним относятся ткани, различающиеся по плотности и типу плетения; моно- и полифиламентные (плетеные и крученые) нити; трикотаж, применяемый в хирургии для изготовления имплантатов (например, поддерживающих устройств желудочков сердца) и эксплантатов. Переплетение волокон и нитей, образующее множественные фрикционные контакты, в значительной степени определяет функциональные (фиксирующие и манипуляционные) свойства тканых материалов и изделий [1].

Аналогичные контакты возникают при связывании нитей. В частности, при формировании хирургического шва в процессе сложной операции выполняются сотни узлов, число которых возрастает при использовании наиболее распространенных синтетических монофиламентных нитей. Такие нити, имеющие благодаря гладкой поверхности высокую биоинертность, в то же время являются относительно жесткими по сравнению с плетеными и кручеными полифиламентными нитями и для надежной фиксации требуют выполнения 4 и более узлов [2, 3], что усложняет процедуру операции.

В связи с вышесказанным разработчики нитей и тканых материалов обычно стремятся улучшить фиксацию переплетений и узлов. Вместе с тем, в ряде

а

б

Рис. 1. Узел (а) и контактное сопряжение нитей (б) биомедицинских приложений, напротив, требуется обеспечить относительную подвижность нитей в тканых материалах.

Можно заметить, что оптимальные показатели качества тканых и шовных материалов обеспечиваются в определенном диапазоне значений параметров трения и деформирования. Однако существующая характеризация свойств обсуждаемых материалов основана на субъективных, качественных оценках («удобные», «мягкие», «хорошо формуемые», «эластичные», «скользкие» и т.д.) [2]. Для объективной и точной оценки необходимы методы прогнозирования фиксирующих свойств тканей и нитей исходя из фрикционно-механических свойств базовых материалов. В настоящем исследовании фиксация нитей в шовных материалах и тканях анализируется путем решения соответствующих контактных задач в объемной постановке.

Формулировка задачи

Как отмечено выше, функциональные свойства тканей, а также прочность и жесткость узловых соединений нитей в значительной степени определяются параметрами контактирования. Так, в обычном узле (рис. 1а) можно выделить два типичных и одинаковых (вследствие симметрии) фрикционных контакта, образованных налеганием искривленных участков нитей (рис. 1б). Аналогичным является сопряжение основы и утка в тканях различного плетения (саржа, сатин и т.д.).

Контактные параметры (проскальзывание, распределение давлений и касательных напряжений), в свою очередь, являются функциями модуля упругости, коэффициента Пуассона, предела пластичности и коэффициента трения материала нитей, которые могут регулироваться в широких пределах и определяться посредством стандартных фрикционно-механических испытаний.

Для сравнительного анализа фиксирующей способности соединения, характерного для переплетения нитей в тканых материалах, в настоящем исследовании рассматривали сопряжение скрещенных цилиндрических тел в предположении упругого и упругопластического деформирования с трением по закону Кулона– Амонтона (при постоянном коэффициенте трения). Расчет производили методом конечных элементов при помощи программного продукта ANSYS [4].

Результаты численного анализа

Моделирование тканого материала

В первой серии расчетов анализировалось напряженно-деформированное состояние при действии только сжимающей нагрузки. Задавались модуль упругости E = 5 ГПа и коэффициент Пуассона материала v = 0,4, коэффициент трения f = 0,3. Приемлемую точность определения касательных напряжений (напряжений трения) при небольших вычислительных затратах показал 4-й уровень дискретизации (табл. 1), который использовался в дальнейшем.

Таблица 1

Зависимость максимальных значений параметров контакта от уровня дискретизации

Уровень дискретизации	4	3	2	1
Контактное давление p , МПа	106	183	160	141
Касательное напряжение τ, МПа	7,63	9,09	6,24	7,06
Проскальзывание u , мм	0,108	0,105	0,094	0,056
Время счета t , мин	17	36	126	310

Далее была исследована возможность управления контактными параметрами путем использования тонких низкомодульных бионейтральных покрытий [5], ауксетичных материалов и материалов с выраженным пределом текучести.

Предполагалось, что коэффициент Пуассона, как мера сжимаемости материала, оказывает влияние на фиксацию нити в узловом соединении. Это обусловлено тем, что контактная жесткость и проскальзывание при контактном деформировании существенно зависят от сжимаемости.

Весьма заметно указанные контактные характеристики изменяются при изменении знака коэффициента Пуассона. Отрицательным коэффициентом Пуассона обладают так называемые ауксетичные материалы, способные расширяться в направлении, перпендикулярном направлению растяжения (подробное описание ауксетиков дано в обзоре [6]). Возможность существования материалов с отрицательным коэффициентом Пуассона подтверждена экспериментально и согласуется с известным соотношением классической теории упругости изотропных тел [7] в виде: v = (3 K - 2 ц )/(6 K + 2 ц ), где ц , К - модули сдвига и объемной деформации, положительные для материалов со стабильной структурой. Отсюда следует, что отрицательные значения v возможны при условии ц >  3/2 К, когда модуль сдвига превышает модуль объемной деформации более, чем на 50%. Таким образом, коэффициент Пуассона изотропного тела может варьироваться в пределах - 1 < v <  0,5. Верхний предел соответствует несжимаемым материалам типа резины, объем которых остается постоянным при значительном изменении формы, нижний – материалам, сохраняющим геометрические пропорции при изменяющемся объеме.

Для описания деформирования нитей из упругопластического материала с линейным упрочнением задавали предел текучести σ тек = 3 МПа и модуль упрочнения Е _упр = 1 ГПа. Нити с покрытием моделировались как слоистые цилиндрические тела.

Результаты расчета параметров контакта при сжатии приведены в табл. 2.

Таблица 2

Оценка влияния управляющих факто ров на максимальные значения контактных параметров Коэффициент Пуссона 0,48 0,4 0,4* 0,4** 0,3 0,0 -0,3 -1 Контактное давление p, МПа 116 106 83,7 18,7 101 102 119 782 Касательное напряжение τ, МПа 7,99 7,63 4,76 1,03 7,28 6,66 6,72 21,3 Проскальзывание u, мм 0,113 0,108 0,427 1,462 0,103 0,105 0,144 0,302 Время счета t, мин 23 17 130 15 14 12 17 10 * наличие бионейтрального эластичного покрытия ** учет пластичности

Можно заметить, что низкомодульное покрытие способствует уменьшению контактных давлений (трудоемкость конечно-элементного решения существенно повышается из-за сгущения сетки при дискретизации тонкого слоя). В предельных случаях несжимаемых и, в особенности, ауксетичных материалов, максимальные значения параметров возрастают. Так, для ауксетика, имеющего коэффициент Пуассона v = - 1 (минимальное значение для изотропной упругой среды) контактное давление возрастает в 6,7 раза в сравнении с практически несжимаемым эластомером ( v = 0,48), максимальное касательное напряжение и проскальзывание увеличиваются в 2,7 раза. При наличии физической нелинейности в виде упругопластического деформирования контактные давления и касательные напряжения существенно снижаются, а проскальзывание, напротив, возрастает.

Вторая серия расчетов позволила изучить напряженно-деформированное состояние контакта при сдвиговой деформации тканого материала в срединной плоскости (табл. 3). Производилось пошаговое увеличение сдвига до достижения его предельного значения, при котором проскальзывание переходило в скольжение. Перемещение сдвига ( u z ) по отношению к заданному и неизменному в процессе расчета нормальному сближению (сжатию) контактирующих нитей ( и ) характеризовалось параметром k = u_z / u y (табл. 3).

Для использованных в расчете исходных данных предельная величина сдвига соответствует к ~ 1,5. Сдвиг приводит к небольшому снижению максимального контактного давления, значительному росту касательного напряжения и быстрому развитию проскальзывания. Низкомодульное покрытие способствует заметному (около 30%) снижению проскальзывания, т.е. улучшению фиксации сопряженных нитей и формостабильности тканого материала в целом.

Моделирование узлового соединения

Эластичность шовного соединения и его способность воспринимать нагрузку в послеоперационный период определяются жесткостью и прочностью нити, в том числе в зонах формирования узлов. В частности, в настоящем исследовании оценка прочности материала нити в узле производилась путем расчета эквивалентных напряжений по критерию Мизеса

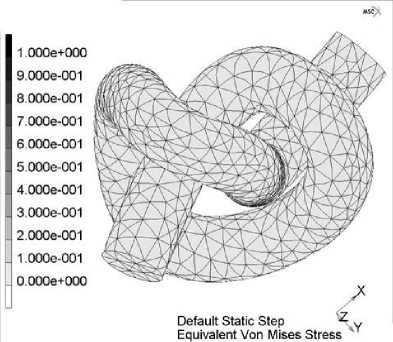
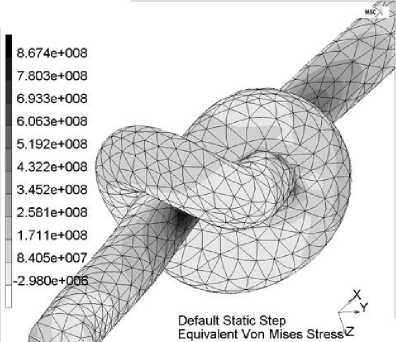
а                               б

Рис. 3. Конечно-элементная модель узла на начальной стадии формирования (а), эквивалентные напряжения в нити (б)

О e = (0,5((с x — О у ) ² + (с у — О z ) ² + (о z — О x ) ² + 6 (о xy ² + С yz ² + О xz ²))) 1/² , где о _x , о _у , о _z , о _xy , о _yz , о _xz - компоненты тензора напряжений.

Таблица 3

Зависимость максимальных значений контактных параметров от безразмерного перемещения k = u z / u y

Параметр сдвига k	1,5*	1,5	1,0	0,8	0,6	0,4	0,2	0,1
Контактное давление p , МПа	85,1	95,2	98,0	98,7	98,6	99,2	99,2	99,5
Касательное напряжение τ, МПа	25,5	28,6	29,4	29,6	29,2	21,3	12,5	9,07
Проскальзывание u , мм	3,28	4,26	2,14	1,31	0,72	0,48	0,28	0,21

* Наличие бионейтрального упругого покрытия

Напряженно-деформированное состояние узла, формируемого при выполнении шва (рис. 1а), определялось при следующих исходных данных: диаметр нити 0,36 мм, модуль упругости материала E = 1 ГПа, коэффициент Пуассона ν = 0,4 и коэффициент трения f = 0,4. Для получения конечно-элементного решения использовали программный продукт Marc [8].

Распределения эквивалентных напряжений и параметров контакта непрерывно изменяются в процессе затягивания узла, что можно проследить путем пошагового решения. В частности, согласно рис. 2, на котором приведены результаты для двух моментов времени, напряженное состояние нити при затягивании узла характеризуется значительной неоднородностью и высокими значениями напряжений в приповерхностном слое (рис. 2б). Нужно отметить, что решение данной задачи является весьма трудоемким (множественный контакт, объемная постановка, большие деформации). Предполагается развитие модели с целью учета пластических деформаций и бионейтрального покрытия нити.

Заключение

Анализ контактного взаимодействия в узловых соединениях тканей и нитей хирургического назначения показывает, что применение низкомодульных полимерных покрытий и ауксетичных материалов, имеющих отрицательный коэффициент Пуассона, является средством управления деформационно-прочностными свойствами тканых и шовных материалов. Установлено, что эквивалентные напряжения, определяющие прочность нити, в процессе затягивания узла непрерывно изменяются, а пространственное распределение указанных напряжений характеризуется значительной неоднородностью и концентрацией в приповерхностном слое нити.